Bu eğitimde, Excel'de bulunan tüm eğilim çizgisi seçeneklerinin ve bunların ne zaman kullanılacağının ayrıntılı açıklamasını bulacaksınız. Ayrıca, bir eğilim çizgisi denklemini bir grafikte nasıl görüntüleyeceğinizi ve eğilim çizgisinin eğimini nasıl bulacağınızı da öğreneceksiniz.

Excel'de bir eğilim çizgisi eklemek çok kolaydır. Tek gerçek zorluk, analiz ettiğiniz veri türüne en uygun eğilim çizgisi türünü seçmektir. Bu eğitimde, Excel'de mevcut olan tüm eğilim çizgisi seçeneklerinin ve bunların ne zaman kullanılacağının ayrıntılı açıklamasını bulacaksınız. Bir Excel grafiğine nasıl eğilim çizgisi ekleyeceğinizi arıyorsanız, lütfen yukarıda bağlantısı verilen eğitime göz atın.

Excel eğilim çizgisi türleri

Excel'de bir eğilim çizgisi eklerken, aralarından seçim yapabileceğiniz 6 farklı seçeneğiniz vardır. Ayrıca Microsoft Excel, bir grafikte eğilim çizgisi denkleminin ve R-kare değerinin görüntülenmesine izin verir:

• Trend çizgisi denklemi veri noktalarına en iyi uyan doğruyu bulan bir formüldür.
• R-kare değeri eğilim çizgisi güvenilirliğini ölçer - R2 1'e ne kadar yakınsa, eğilim çizgisi verilere o kadar iyi uyar.

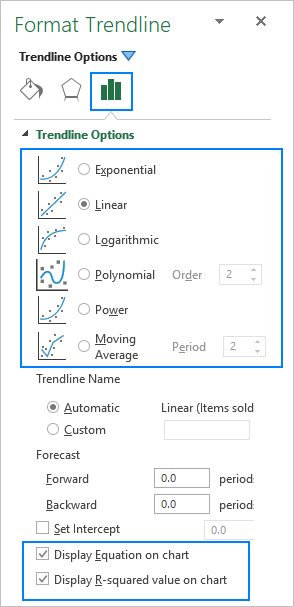
Aşağıda, grafik örnekleriyle birlikte her bir trend çizgisi türünün kısa bir açıklamasını bulacaksınız.

Doğrusal eğilim çizgisi

Doğrusal eğilim çizgisi, bir grafikteki veri noktaları düz bir çizgiye benzediğinde doğrusal veri setleriyle kullanılmak için en iyisidir. Tipik olarak, doğrusal bir eğilim çizgisi zaman içinde sürekli bir yükselişi veya düşüşü tanımlar.

Örneğin, aşağıdaki doğrusal eğilim çizgisi 6 ay boyunca satışlarda istikrarlı bir artış olduğunu göstermektedir. 0,9855'lik R2 değeri, tahmini eğilim çizgisi değerlerinin gerçek verilere oldukça iyi uyduğunu göstermektedir.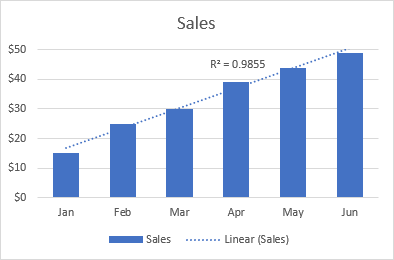

Üstel eğilim çizgisi

Üstel eğilim çizgisi, veri değerlerindeki artış veya düşüşü artan bir oranda gösteren kavisli bir çizgidir, bu nedenle çizgi genellikle bir tarafta daha kavislidir. Bu eğilim çizgisi türü genellikle bilimlerde, örneğin insan nüfusundaki artışı veya vahşi yaşam popülasyonlarındaki düşüşü görselleştirmek için kullanılır.

Sıfır veya negatif değerler içeren veriler için üstel bir eğilim çizgisi oluşturulamayacağını lütfen unutmayın.

Üstel eğriye iyi bir örnek, dünya üzerindeki tüm vahşi kaplan nüfusundaki azalmadır.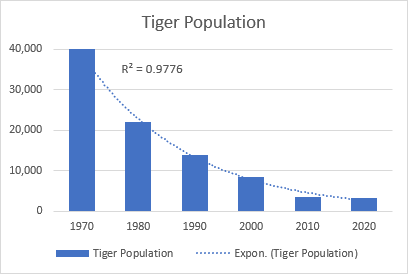

Logaritmik eğilim çizgisi

Logaritmik en iyi uyum çizgisi genellikle hızla artan veya azalan ve ardından düzleşen verileri çizmek için kullanılır. Hem pozitif hem de negatif değerleri içerebilir.

Logaritmik eğilim çizgisine örnek olarak, önce yükselen ancak bir süre sonra istikrar kazanan enflasyon oranı verilebilir.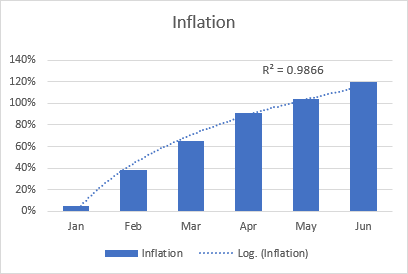

Polinom eğilim çizgisi

Polinom eğrisel eğilim çizgisi, birden fazla yükseliş ve düşüşe sahip salınımlı değerlere sahip büyük veri setleri için iyi çalışır.

Genel olarak, bir polinom en büyük üssün derecesine göre sınıflandırılır. Polinom eğilim çizgisinin derecesi, bir grafikteki bükülme sayısına göre de belirlenebilir. Tipik olarak, ikinci dereceden bir polinom eğilim çizgisinde bir bükülme (tepe veya vadi), kübik bir polinomda 1 veya 2 bükülme ve kuartik bir polinomda 3'e kadar bükülme vardır.

Bir Excel grafiğine polinom eğilim çizgisi eklerken, dereceyi aşağıdaki kutuya karşılık gelen sayıyı yazarak belirtirsiniz Sipariş kutusunun üzerinde Trend Çizgisini Biçimlendir bölmesi, varsayılan olarak 2'dir: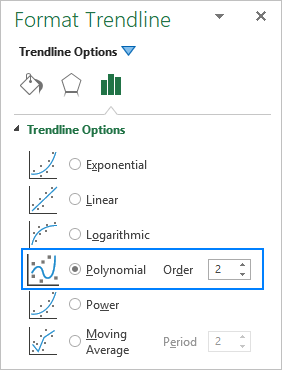

Örneğin, kar ile ürünün piyasada bulunduğu yıl sayısı arasındaki ilişkiyi gösteren aşağıdaki grafikte ikinci dereceden polinom eğilimi açıkça görülmektedir: başlangıçta yükseliş, ortada zirve ve sona yakın düşüş.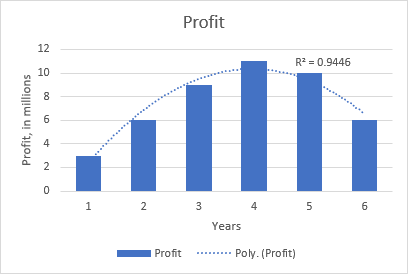

Güç eğilim çizgisi

Güç eğilim çizgisi üstel eğriye çok benzer, sadece daha simetrik bir yayı vardır. Genellikle belirli bir oranda artan ölçümleri çizmek için kullanılır.

Sıfır veya negatif değerler içeren bir Excel grafiğine güç eğilim çizgisi eklenemez.

Örnek olarak, kimyasal reaksiyon hızını görselleştirmek için bir güç eğilim çizgisi çizelim. 0,9918'lik R-kare değerine dikkat edin, bu da eğilim çizgimizin verilere neredeyse mükemmel bir şekilde uyduğu anlamına gelir.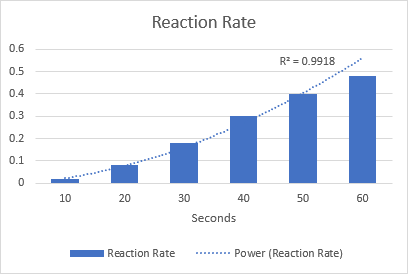

Hareketli ortalama eğilim çizgisi

Grafiğinizdeki veri noktalarında çok fazla iniş çıkış olduğunda, hareketli ortalama eğilim çizgisi, bir modeli daha net göstermek için veri değerlerindeki aşırı dalgalanmaları yumuşatabilir. Bunun için Excel, belirttiğiniz dönem sayısının (varsayılan olarak 2) hareketli ortalamasını hesaplar ve bu ortalama değerleri çizgiye nokta olarak koyar. Dönem değeri, çizgi ne kadar düzgün olursa.

İyi bir pratik örnek, aksi takdirde gözlemlenmesi zor olan bir hisse senedi fiyatındaki dalgalanmaları ortaya çıkarmak için hareketli ortalama eğilim çizgisini kullanmaktır.

Daha fazla bilgi için lütfen bkz: Bir Excel grafiğine hareketli ortalama eğilim çizgisi nasıl eklenir.

Excel eğilim çizgisi denklemleri ve formülleri

Bu bölümde Excel'in farklı eğilim çizgisi türleri için kullandığı denklemler açıklanmaktadır. Bu formülleri manuel olarak oluşturmanız gerekmez, Excel'e eğilim çizgisi denklemini bir grafikte görüntülemesini söylemeniz yeterlidir.

Ayrıca, bir eğilim çizgisinin eğimini ve diğer katsayıları bulma formülünü tartışacağız. Formüller, 2 değişken kümesine sahip olduğunuzu varsayar: bağımsız değişken x ve bağımlı değişken y Çalışma sayfalarınızda, tahmin edilen değerleri elde etmek için bu formülleri kullanabilirsiniz y değerlerinin herhangi bir değeri için x .

Tutarlılık için, tüm örneklerde aynı veri setini biraz değişen değerlerle kullanacağız. Ancak, bunun yalnızca gösterim amaçlı olduğunu lütfen unutmayın. Gerçek çalışma sayfalarınızda, veri türünüze karşılık gelen eğilim çizgisi türünü seçmelisiniz.

Önemli not! Eğilim çizgisi formülleri yalnızca aşağıdakilerle birlikte kullanılmalıdır XY dağılım grafikleri çünkü sadece bu grafik her iki x ve y Daha fazla bilgi için lütfen Excel eğilim çizgisi denkleminin neden yanlış olabileceğine bakın.

Doğrusal eğilim çizgisi denklemi ve formülleri

Doğrusal eğilim çizgisi denklemi, en küçük kareler yöntemlerini kullanarak eğim ve kesmek katsayılar öyle ki:

Nerede?

• b bu eğim bir trend çizgisinin.
• a bu y-kesişimi 'nin beklenen ortalama değeri olan y tüm x değişkenler 0'a eşittir. Bir grafikte, trend çizgisinin y Eksen.

Doğrusal regresyon için Microsoft Excel, eğim ve kesişim katsayılarını elde etmek için özel işlevler sağlar.

Eğilim çizgisinin eğimi

b: =SLOPE(y,x)

Y-kesişimi

a: =INTERCEPT(y,x)

Varsayalım ki x aralığı B2:B13 ve y aralığı C2:C13'tür, gerçek hayattaki formüller aşağıdaki gibidir:

= EĞIM(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Aynı sonuçlar, LINEST fonksiyonunu aşağıdaki gibi kullanarak da elde edilebilir dizi formülü Bunun için aynı satırda 2 bitişik hücre seçin, formülü girin ve tamamlamak için Ctrl + Shift + Enter tuşlarına basın:

=LINEST(C2:C13,B2:B13)

Aşağıdaki ekran görüntüsünde gösterildiği gibi, formüller tarafından döndürülen eğim ve kesişim katsayıları, grafikte görüntülenen doğrusal eğilim çizgisi denklemindeki katsayılarla mükemmel bir şekilde uyumludur, sadece ikincisi 4 ondalık basamağa yuvarlanmıştır: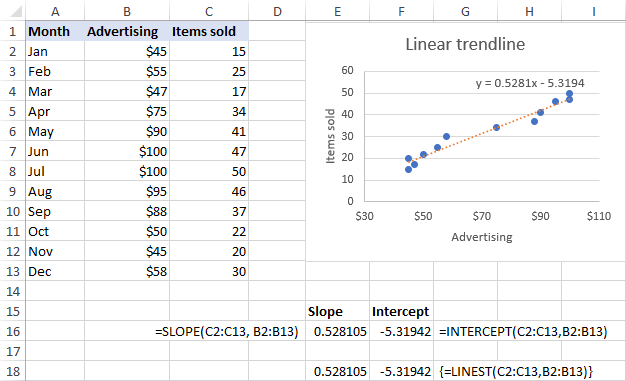

Üstel eğilim çizgisi denklemi ve formülleri

Üstel eğilim çizgisi için Excel aşağıdaki denklemi kullanır:

Nerede a ve b hesaplanan katsayılardır ve e matematiksel sabit e'dir (doğal logaritmanın tabanı).

Katsayılar bu genel formüller kullanılarak hesaplanabilir:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Örnek veri setimiz için formüller aşağıdaki şekli alır:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logaritmik eğilim çizgisi denklemi ve formülleri

İşte Excel'deki logaritmik eğilim çizgisi denklemi:

Nerede a ve b sabitlerdir ve ln doğal logaritma fonksiyonudur.

Sabitleri elde etmek için, sadece son argümanda farklılık gösteren bu genel formülleri kullanın:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Örnek veri setimiz için bunları kullanıyoruz:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polinom eğilim çizgisi denklemi ve formülleri

Polinom eğilim çizgisini hesaplamak için Excel bu denklemi kullanır:

Nerede b ₁ ... b ₆ ve a sabitlerdir.

Polinom eğilim çizginizin derecesine bağlı olarak, sabitleri elde etmek için aşağıdaki formül setlerinden birini kullanın.

Kuadratik (2. derece) polinom eğilim çizgisi

Denklem: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kübik (3. derece) polinom eğilim çizgisi

Denklem: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Daha yüksek dereceli polinom eğilim çizgileri için formüller aynı model kullanılarak oluşturulabilir.

Veri setimiz için 2. dereceden polinom eğilim çizgisi daha uygundur, bu nedenle bu formülleri kullanıyoruz:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)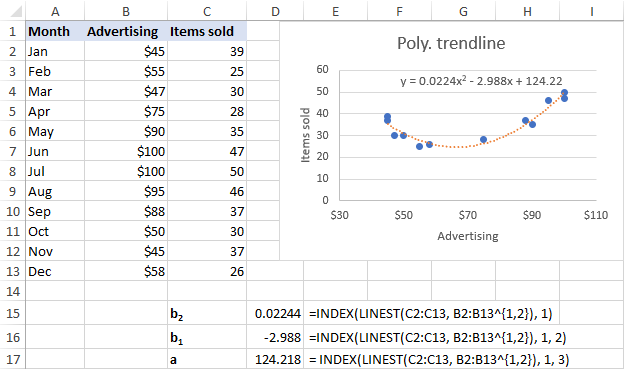

Güç trend çizgisi denklemi ve formülleri

Bu basit denkleme dayalı olarak Excel'de bir güç eğilim çizgisi çizilir:

Nerede a ve b bu formüllerle hesaplanabilen sabitlerdir:

a: =EXP(INDEX(LINEST(LN(y), LN(x),), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),), 1)

Bizim durumumuzda, aşağıdaki formüller işe yaramaktadır:

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),), 1)

Excel eğilim çizgisi denklemi yanlış - nedenleri ve düzeltmeleri

Excel'in bir eğilim çizgisini yanlış çizdiğini veya grafiğinizde görüntülenen eğilim çizgisi formülünün yanlış olduğunu düşünüyorsanız, aşağıdaki iki nokta duruma biraz ışık tutabilir.

Excel eğilim çizgisi denklemi yalnızca dağılım grafiklerinde doğrudur

Excel eğilim çizgisi formülleri yalnızca XY (dağılım) grafikleriyle kullanılmalıdır çünkü yalnızca bu grafik türünde hem y ekseni hem de x ekseni sayısal değerler olarak çizilir.

Çizgi grafiklerde, sütun ve çubuk grafiklerde, sayısal değerler yalnızca y ekseninde çizilir. x ekseni, eksen etiketlerinin sayı veya metin olmasına bakılmaksızın doğrusal bir seriyle (1, 2, 3, ...) temsil edilir. Bu grafiklerde bir eğilim çizgisi oluşturduğunuzda, Excel eğilim çizgisi formülünde varsayılan x değerlerini kullanır.

Excel eğilim çizgisi denkleminde sayılar yuvarlanır

Grafikte daha az yer kaplamak için Excel, bir eğilim çizgisi denkleminde çok az anlamlı basamak görüntüler. Tasarım açısından güzel olsa da, denklemde x değerlerini manuel olarak sağladığınızda formülün doğruluğunu önemli ölçüde azaltır.

Denklemde daha fazla ondalık basamak göstermek kolay bir çözümdür. Alternatif olarak, eğilim çizgisi türünüze karşılık gelen bir formül kullanarak katsayıları hesaplayabilir ve formül hücrelerini yeterli sayıda ondalık basamak gösterecek şekilde biçimlendirebilirsiniz. Ondalık Artışı üzerindeki Ev sekmesindeki Sayı Grup.

Excel'de farklı eğilim çizgisi türlerini bu şekilde oluşturabilir ve denklemlerini alabilirsiniz. Okuduğunuz için teşekkür ediyor ve gelecek hafta blogumuzda görüşmeyi umuyorum!