Այս ձեռնարկում դուք կգտնեք Excel-ում հասանելի բոլոր միտումների ընտրանքների մանրամասն նկարագրությունը և երբ դրանք օգտագործել: Դուք նաև կսովորեք, թե ինչպես ցուցադրել միտումի գծի հավասարումը գծապատկերում և գտնել միտումի գծի թեքությունը:

Excel-ում շատ հեշտ է միտում ավելացնել: Միակ իրական մարտահրավերն այն է, որ ընտրել տենդենցի տեսակը, որը լավագույնս համապատասխանում է ձեր վերլուծած տվյալների տեսակին: Այս ձեռնարկում դուք կգտնեք Excel-ում առկա բոլոր միտումների ընտրանքների մանրամասն նկարագրությունը և երբ դրանք օգտագործել: Եթե ​​փնտրում եք, թե ինչպես տեղադրել միտումների գիծ Excel-ի գծապատկերում, խնդրում ենք ստուգել վերը նշված ուղեցույցը:

Excel-ի միտումների տեսակները

Excel-ում միտում ավելացնելիս , դուք ունեք 6 տարբեր տարբերակներ ընտրելու համար: Բացի այդ, Microsoft Excel-ը թույլ է տալիս գծապատկերում ցուցադրել տրենդի գծի հավասարումը և R-քառակուսի արժեքը:

• Միջումային հավասարումը բանաձև է, որը գտնում է տվյալների կետերին լավագույնս համապատասխանող գիծը:
• R-քառակուսի արժեքը չափում է միտումի գծի հուսալիությունը. որքան R2-ը մոտ լինի 1-ին, այնքան տենդենցի գիծը ավելի լավ է համապատասխանում տվյալներին:

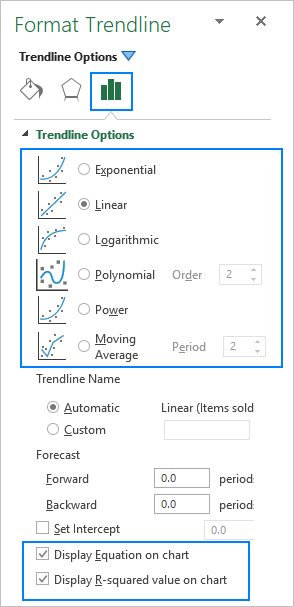
Ստորև դուք կգտնեք յուրաքանչյուր միտումի տիպի հակիրճ նկարագրությունը գծապատկերների օրինակներով:

Գծային միտում

Գծային միտումի գիծը լավագույնն է լինել օգտագործվում է գծային տվյալների հավաքածուներով, երբ գծապատկերում տվյալների կետերը նման են ուղիղ գծի: Սովորաբար, գծային միտումը նկարագրում է շարունակական աճ կամ անկումժամանակի ընթացքում:

Օրինակ, հետևյալ գծային միտումը ցույց է տալիս վաճառքի կայուն աճ 6 ամսվա ընթացքում: Իսկ R2 արժեքը՝ 0,9855, ցույց է տալիս գնահատված միտումների արժեքների բավականին լավ համապատասխանությունը իրական տվյալներին: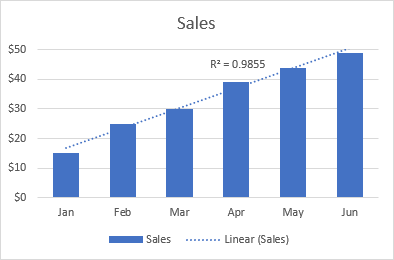

Էքսպոնենցիալ միտումի գիծ

Էքսպոնենցիալ միտումի գիծը կոր գիծ է, որը ցույց է տալիս տվյալների արժեքների աճը կամ անկումը աճող արագությամբ, հետևաբար գիծը սովորաբար ավելի կոր է մի կողմից: Միտման գծի այս տեսակը հաճախ օգտագործվում է գիտության մեջ, օրինակ՝ պատկերացնելու համար մարդկային բնակչության աճը կամ վայրի բնության պոպուլյացիաների նվազումը:

Խնդրում ենք նկատի ունենալ, որ զրո կամ բացասական արժեքներ պարունակող տվյալների համար չի կարող ստեղծվել էքսպոնենցիոնալ միտում:

Էքսպոնենցիալ կորի լավ օրինակ է երկրագնդի վայրի վագրի ամբողջ պոպուլյացիայի քայքայումը: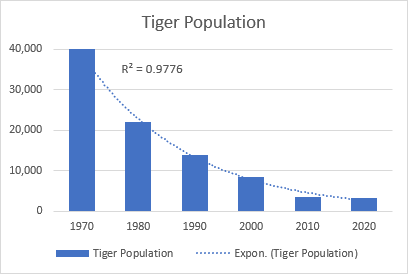

Լոգարիթմական միտման գիծը

Լոգարիթմական լավագույն պիտանի գիծը սովորաբար օգտագործվում է տվյալների գծագրման համար, որոնք արագ աճում կամ նվազում են, իսկ հետո մակարդակը իջնում ​​է: Այն կարող է ներառել ինչպես դրական, այնպես էլ բացասական արժեքներ:

Լոգարիթմական միտումի գծի օրինակ կարող է լինել գնաճի մակարդակը, որը սկզբում բարձրանում է, բայց որոշ ժամանակ անց կայունանում է: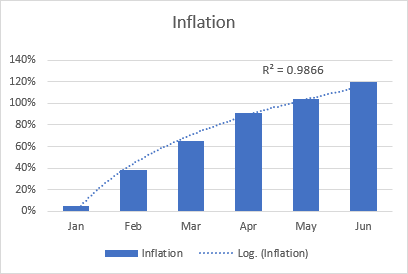

Բազմանանդամ տենդենցային գիծ

Բազմանանդամ կորագիծ գիծը լավ է աշխատում մեծ տվյալների հավաքածուների համար` տատանվող արժեքներով, որոնք ունեն մեկից ավելի բարձրացում և անկում:

Ընդհանրապես, բազմանդամը դասակարգվում է ըստ ամենամեծ ցուցանիշի աստիճանը. Բազմանդամի միտումի գծի աստիճանը կարող էորոշվում է նաև գրաֆիկի թեքությունների քանակով: Սովորաբար, քառակուսի բազմանդամը ունի մեկ թեք (բլուր կամ հովիտ), խորանարդ բազմանդամը՝ 1 կամ 2 թեք, իսկ քառանդամ բազմանդամը՝ մինչև 3 թեք: Դուք նշում եք աստիճանը՝ մուտքագրելով համապատասխան թիվը Պատվիրել վանդակում Ձևաչափել Trendline վահանակում, որը լռելյայն 2 է.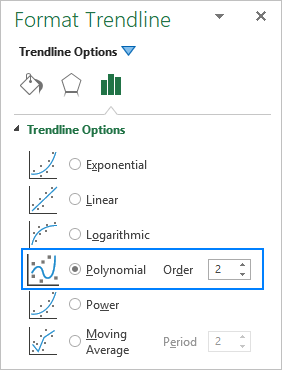

Օրինակ, քառակուսի բազմանդամ միտումը ակնհայտ է հետևյալ գծապատկերում, որը ցույց է տալիս կապը շահույթի և այն տարիների քանակի միջև, որը ապրանքը հայտնվել է շուկայում. սկզբում բարձրացում, միջինում բարձրացում և վերջում անկում: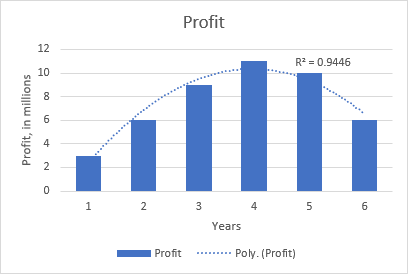

Հզորության միտում

Էլեկտրական տենդենցի գիծը շատ նման է էքսպոնենցիալ կորին, միայն այն ունի ավելի սիմետրիկ աղեղ: Այն սովորաբար օգտագործվում է որոշակի արագությամբ աճող չափումներ գծագրելու համար:

Հզորության միտումը չի կարող ավելացվել Excel գծապատկերում, որը պարունակում է զրո կամ բացասական արժեքներ:

Որպես օրինակ, եկեք նկարենք հզորության գիծ՝ քիմիական ռեակցիայի արագությունը պատկերացնելու համար: Նկատի ունեցեք R-քառակուսի արժեքը 0,9918, ինչը նշանակում է, որ մեր միտումների գիծը գրեթե լիովին համապատասխանում է տվյալներին: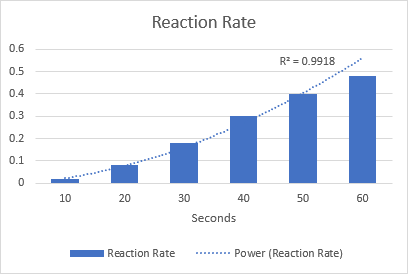

Շարժվող միջին միտումի գիծը

Երբ ձեր գծապատկերում տվյալների կետերը շատ վերելքներ ու անկումներ են ունենում, շարժվող միջին միտումի գիծը կարող է հարթել տվյալների արժեքների ծայրահեղ տատանումները՝ օրինաչափությունն ավելի հստակ ցույց տալու համար: Դրա համար Excel-ը հաշվարկում էՁեր նշած ժամանակաշրջանների քանակի շարժվող միջինը (2 ըստ լռելյայն) և այդ միջին արժեքները դնում է որպես գծի կետեր: Որքան բարձր է Period արժեքը, այնքան ավելի հարթ է գիծը:

Լավ գործնական օրինակ է օգտագործել շարժվող միջին միտումի գիծը` բացահայտելու բաժնետոմսերի գնի տատանումները, որոնք հակառակ դեպքում դժվար կլիներ դիտարկել:

Լրացուցիչ տեղեկությունների համար տե՛ս. Ինչպես ավելացնել շարժվող միջին գիծը Excel-ի գծապատկերում:

Excel-ի միտումների գծի հավասարումներ և բանաձևեր

Այս բաժինը նկարագրում է այն հավասարումները, որոնք օգտագործում է Excel-ը միտումների տարբեր տեսակների համար: Պետք չէ ձեռքով ստեղծել այս բանաձևերը, պարզապես ասեք Excel-ին, որ ցուցադրի տրենդի գծի հավասարումը գծապատկերում:

Նաև մենք կքննարկենք տենդենցի գծի թեքությունը գտնելու բանաձևը և այլ գործակիցներ: Բանաձևերը ենթադրում են, որ դուք ունեք փոփոխականների 2 խումբ՝ անկախ փոփոխական x և կախված փոփոխական y : Ձեր աշխատաթերթերում դուք կարող եք օգտագործել այս բանաձևերը՝ ստանալու համար կանխատեսված y արժեքները x -ի ցանկացած տրված արժեքի համար:

Հետևողականության համար մենք կօգտագործենք նույն տվյալները: մի փոքր տարբերվող արժեքներով բոլոր օրինակների համար: Այնուամենայնիվ, խնդրում ենք նկատի ունենալ, որ դա միայն ցուցադրական նպատակներով է: Ձեր իրական աշխատաթերթերում դուք պետք է ընտրեք ձեր տվյալների տեսակին համապատասխան միտումի գիծ:

Կարևոր նշում: Թրենդային բանաձևերը պետք է օգտագործվեն միայն XY ցրման գծապատկերներով , քանի որ միայն սագծապատկերը պատկերում է և՛ x և՛ y առանցքները որպես թվային արժեքներ: Լրացուցիչ տեղեկությունների համար տե՛ս, թե ինչու է Excel-ի միտումների գծի հավասարումը կարող է սխալ լինել:

Գծային միտումի հավասարում և բանաձևեր

Գծային գծի հավասարումը օգտագործում է նվազագույն քառակուսիների մեթոդները թեքությունը գտնելու համար: և ընդհատում գործակիցներ, ինչպիսիք են.

y = bx + a

Որտեղ:

• b է թեքությունը միտումի գծի:
• a -ը y-հատումն է , որը y -ի ակնկալվող միջին արժեքն է, երբ բոլորը x փոփոխականները հավասար են 0-ի: Գծապատկերում դա այն կետն է, որտեղ միտումի գիծը հատում է y առանցքը:

Գծային ռեգրեսիայի համար Microsoft Excel-ը տրամադրում է հատուկ գործառույթներ` ստանալու համար թեքության և հատման գործակիցները:

Թրենդային գծի թեքություն

b: =SLOPE(y,x)

Y-հատում

a: =INTERCEPT(y,x)

Ենթադրենք, որ x միջակայքը B2:B13 է, իսկ y միջակայքը` C2:C13, իրական բանաձևերը հետևյալն են.

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Նույն արդյունքները կարելի է ձեռք բերել՝ օգտագործելով LINEST ֆունկցիան որպես զանգվածի բանաձև : Դրա համար ընտրեք 2 հարակից բջիջ նույն շարքում, մուտքագրեք բանաձևը և սեղմեք Ctrl + Shift + Enter այն ավարտելու համար. Բանաձևերով վերադարձված գործակիցները միանգամայն համահունչ են գծապատկերում ցուցադրված գծային միտումների հավասարման գործակիցներին, միայն վերջիններս կլորացվում են մինչև 4 տասնորդական տեղեր.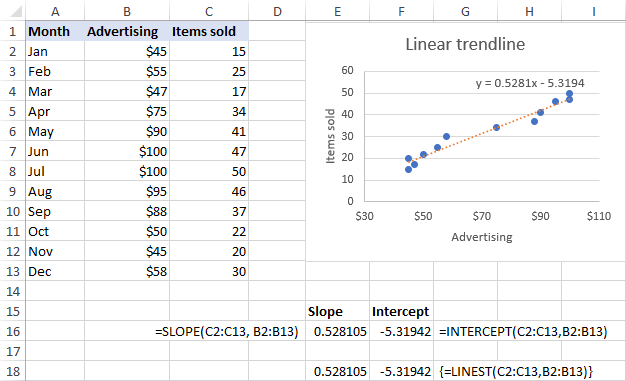

Էքսպոնենցիալ տենդենցային հավասարում և բանաձևեր

Էքսպոնենցիալ միտումի գծի համար Excel-ն օգտագործում է հետևյալ հավասարումը.

y = aebx

Որտեղ a և b հաշվարկված գործակիցներն են, իսկ e-ն մաթեմատիկական հաստատունն է e (բնական լոգարիթմի հիմքը):

Գործակիցները կարող են հաշվարկվել հետևյալ ընդհանուր բանաձևերի միջոցով.

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Մեր նմուշային տվյալների հավաքածուի համար բանաձևերը ստանում են հետևյալ ձևը.

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Թրենդային լոգարիթմական հավասարումը և բանաձևերը

Ահա Excel-ում լոգարիթմական գծի հավասարումը.

y = a*ln(x)+b

Որտեղ a և b հաստատուններ են, իսկ ln բնական լոգարիթմի ֆունկցիան է:

Հաստատունները ստանալու համար օգտագործեք այս ընդհանուր բանաձևերը, որոնք տարբերվում են միայն վերջին արգումենտում.

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Մեր նմուշային տվյալների հավաքածուի համար մենք օգտագործում ենք հետևյալները.

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Բազմանդամ տենդենցային հավասարումը և բանաձևերը

Բազմանանդամների միտումների գիծը մշակելու համար Excel-ն օգտագործում է այս հավասարումը.

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Որտեղ b ₁ … b ₆ և a հաստատուններ են:

Կախված ձեր բազմանդամ ուղղության աստիճանից, օգտագործեք հետևյալ բանաձևերի հավաքածուներից մեկը հաստատունները ստանալու համար:

Քառակորդական (2-րդ կարգի) բազմանդամ միտումի գիծ

Հավասարում` y = b ₂ x2+ b ₁ x + a

բ ₂ ՝ =INDEX(LINEST(y, x^{1,2}), 1)

բ ₁ ՝ =INDEX(LINEST(y, x^{1,2}), 1, 2)

ա: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Խորանարդ (3-րդ կարգի) բազմանդամ միտումի գիծ

Հավասարում` y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Ավելի բարձր աստիճանի բազմանդամ միտումների գծերի բանաձևերը կարող են կառուցվել՝ օգտագործելով միևնույն օրինաչափությունը:

Մեր տվյալների հավաքածուի համար 2-րդ կարգի բազմանդամ միտումների գծերի հավաքածուները ավելի լավ, ուստի մենք օգտագործում ենք հետևյալ բանաձևերը.

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)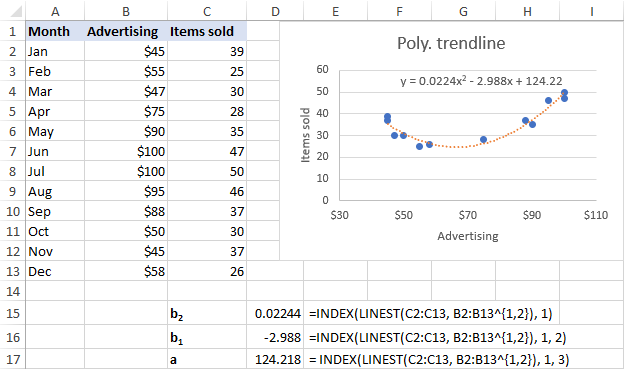

Power trendline-ի հավասարումը և բանաձևերը

Excel-ում էլեկտրաէներգիայի միտումը գծվում է այս պարզ հավասարման հիման վրա.

y = axb

Որտեղ a և b հաստատուններ են, որոնք կարելի է հաշվարկել հետևյալ բանաձևերով.

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

Մեր դեպքում հետևյալ բանաձևերը գործում են :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Excel-ի միտումների հավասարումը սխալ է. պատճառներ և ուղղումներ

Եթե կարծում եք, որ Excel-ը սխալ է գծել միտում կամ ձեր գծապատկերում ցուցադրված միտումի գծի բանաձևը սխալ է, հետևյալ երկու կետերը կարող են որոշակիորեն թուլացնել թեթև իրավիճակի վրա:

Excel-ի միտումների հավասարումը ճիշտ է միայն ցրված գծապատկերներում

Excel-ի միտումների գծի բանաձևերը պետք է օգտագործվեն միայն XY (ցրված) գրաֆիկներով, քանի որ միայն այս գծապատկերում մուտքագրեք երկու y առանցքը: իսկ x-առանցքները գծագրվում են որպես թվային արժեքներ:

Գծային գծապատկերներում, սյունակային և բարակ գծապատկերներում թվային արժեքները գծագրվում են միայն y առանցքի վրա: X առանցքը ներկայացված է գծային շարքով (1, 2,3,…) անկախ նրանից՝ առանցքի պիտակները թվեր են, թե տեքստ: Երբ այս գծապատկերներում գծում եք տենդենցի գիծ, ​​Excel-ն օգտագործում է այդ ենթադրյալ x արժեքները միտումի գծի բանաձևում:

Թվերը կլորացվում են Excel-ի գծի հավասարման մեջ

Գծապատկերում ավելի քիչ տեղ զբաղեցնելու համար Excel-ը ցուցադրում է շատ քիչ նշանակալից թվեր միտումի գծի հավասարման մեջ: Դիզայնի առումով հաճելի է, այն զգալիորեն նվազեցնում է բանաձևի ճշգրտությունը, երբ դուք ձեռքով տրամադրում եք x արժեքներ հավասարման մեջ:

Հեշտ ուղղումը հավասարման մեջ ավելի շատ տասնորդական թվեր ցույց տալն է: Որպես այլընտրանք, դուք կարող եք հաշվարկել գործակիցները՝ օգտագործելով ձեր միտումի գծին համապատասխանող բանաձևը և ձևակերպել բանաձևի բջիջներն այնպես, որ դրանք ցույց տան բավարար թվով տասնորդական տեղեր: Դրա համար պարզապես սեղմեք Ավելացնել տասնորդականը կոճակը Տուն ներդիրում Համար խմբում:

Այդպես կարող եք ստեղծել միտումների տարբեր տեսակներ: Excel-ում և ստանալ դրանց հավասարումները: Շնորհակալ եմ կարդալու համար և հուսով եմ, որ հաջորդ շաբաթ կտեսնենք ձեզ մեր բլոգում: 3>