Inhoudsopgave
In deze handleiding vindt u een gedetailleerde beschrijving van alle in Excel beschikbare trendlijnopties en wanneer deze te gebruiken. U leert ook hoe u een trendlijnvergelijking in een grafiek kunt weergeven en de helling van een trendlijn kunt vinden.
Het is heel eenvoudig om een trendlijn toe te voegen in Excel. De enige echte uitdaging is om het type trendlijn te kiezen dat het best past bij het type gegevens dat u analyseert. In deze handleiding vindt u een gedetailleerde beschrijving van alle trendlijnopties die in Excel beschikbaar zijn en wanneer u ze moet gebruiken. Als u op zoek bent naar hoe u een trendlijn kunt invoegen in een Excel-grafiek, bekijk dan de hierboven gelinkte handleiding.
Excel trendlijntypes
Bij het toevoegen van een trendlijn in Excel kunt u kiezen uit 6 verschillende opties. Bovendien kunt u met Microsoft Excel een trendlijnvergelijking en R-kwadraatwaarde in een grafiek weergeven:
- Trendlijnvergelijking is een formule die een lijn vindt die het beste past bij de gegevenspunten.
- R-kwadraat waarde meet de betrouwbaarheid van de trendlijn - hoe dichter R2 bij 1 ligt, hoe beter de trendlijn bij de gegevens past.
Hieronder vindt u een korte beschrijving van elk type trendlijn met grafiekvoorbeelden.
Lineaire trendlijn
De lineaire trendlijn kan het best worden gebruikt voor lineaire gegevensreeksen wanneer de gegevenspunten in een grafiek op een rechte lijn lijken. Een lineaire trendlijn beschrijft doorgaans een continue stijging of daling in de tijd.
De volgende lineaire trendlijn toont bijvoorbeeld een gestage stijging van de verkoop over 6 maanden. En de R2-waarde van 0,9855 geeft aan dat de geschatte waarden van de trendlijn vrij goed passen bij de werkelijke gegevens. 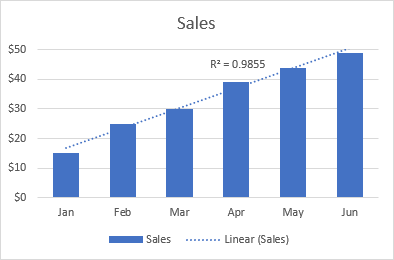
Exponentiële trendlijn
De exponentiële trendlijn is een gebogen lijn die een stijging of daling van de gegevenswaarden in een stijgend tempo illustreert, daarom is de lijn meestal meer gebogen aan één zijde. Dit type trendlijn wordt vaak gebruikt in de wetenschappen, bijvoorbeeld om een groei van de menselijke bevolking of een daling van de populatie van wilde dieren te visualiseren.
Merk op dat een exponentiële trendlijn niet kan worden gecreëerd voor gegevens die nullen of negatieve waarden bevatten.
Een goed voorbeeld van een exponentiële curve is het verval van de gehele wilde tijgerpopulatie op aarde. 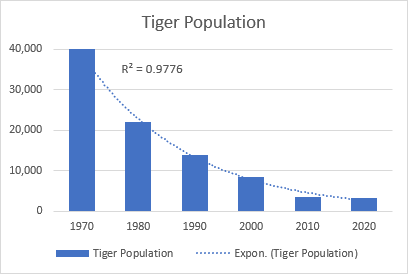
Logaritmische trendlijn
De logaritmische best-fit lijn wordt meestal gebruikt om gegevens uit te zetten die snel stijgen of dalen en dan afvlakken. De lijn kan zowel positieve als negatieve waarden bevatten.
Een voorbeeld van een logaritmische trendlijn kan een inflatiecijfer zijn, dat eerst hoger wordt, maar zich na enige tijd stabiliseert. 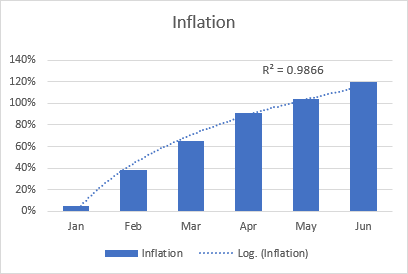
Polynomiale trendlijn
De polynomiale curvilineaire trendlijn werkt goed voor grote gegevensreeksen met oscillerende waarden die meer dan één keer stijgen en dalen.
In het algemeen wordt een polynoom ingedeeld aan de hand van de graad van de grootste exponent. De graad van de polynomiale trendlijn kan ook worden bepaald aan de hand van het aantal bochten in een grafiek. Een kwadratische polynoom heeft doorgaans één bocht (heuvel of dal), een kubische polynoom heeft 1 of 2 bochten, en een kwartische polynoom heeft maximaal 3 bochten.
Wanneer u een polynomiale trendlijn toevoegt in een Excel-grafiek, specificeert u de graad door het overeenkomstige getal te typen in het Bestel vakje op de Formaat Trendline deelvenster, dat standaard op 2 staat: 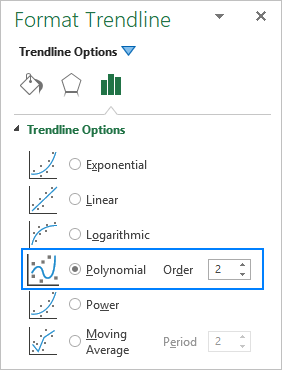
De kwadratische polynomiale trend is bijvoorbeeld duidelijk in de volgende grafiek die het verband toont tussen de winst en het aantal jaren dat het product op de markt is: stijging in het begin, piek in het midden en daling tegen het einde. 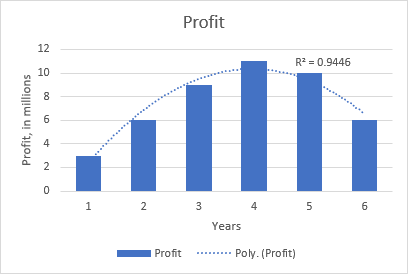
Vermogenstrendlijn
De vermogenstrendlijn lijkt sterk op de exponentiële curve, maar heeft een meer symmetrische boog. Hij wordt gewoonlijk gebruikt om metingen uit te zetten die met een bepaalde snelheid toenemen.
Een powertrendlijn kan niet worden toegevoegd aan een Excel-grafiek die nul of negatieve waarden bevat.
Laten we als voorbeeld een machtstrendlijn tekenen om de chemische reactiesnelheid te visualiseren. Let op de R-kwadraatwaarde van 0,9918, wat betekent dat onze trendlijn bijna perfect past bij de gegevens. 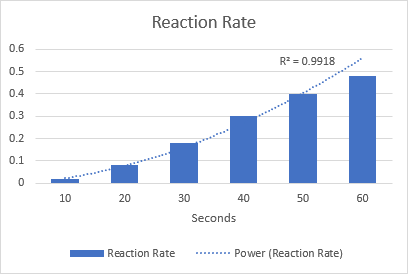
Trendlijn voortschrijdend gemiddelde
Wanneer de gegevenspunten in uw grafiek veel ups en downs hebben, kan een trendlijn met voortschrijdend gemiddelde de extreme schommelingen in de gegevenswaarden afvlakken om een patroon duidelijker te laten zien. Hiervoor berekent Excel het voortschrijdend gemiddelde van het aantal perioden dat u opgeeft (standaard 2) en zet die gemiddelde waarden als punten in de lijn. Hoe hoger de Periode waarde, hoe vloeiender de lijn.
Een goed praktijkvoorbeeld is het gebruik van de trendlijn van het voortschrijdend gemiddelde om schommelingen in een aandelenprijs aan het licht te brengen die anders moeilijk waarneembaar zouden zijn. 
Zie voor meer informatie: Hoe voeg je een trendlijn van een voortschrijdend gemiddelde toe aan een Excel-grafiek?
Excel-trendlijnvergelijkingen en -formules
Dit hoofdstuk beschrijft de vergelijkingen die Excel gebruikt voor verschillende soorten trendlijnen. U hoeft deze formules niet handmatig op te stellen, maar vertelt Excel gewoon om de trendlijnvergelijking in een grafiek weer te geven.
Ook bespreken we de formule om de helling van een trendlijn en andere coëfficiënten te vinden. De formules gaan ervan uit dat je 2 reeksen variabelen hebt: onafhankelijke variabele x en afhankelijke variabele y In je werkbladen kun je deze formules gebruiken om de voorspelde y waarden voor bepaalde waarden van x .
Voor de consistentie gebruiken we voor alle voorbeelden dezelfde dataset met licht verschillende waarden. Houd er echter rekening mee dat dit alleen voor demonstratiedoeleinden is. In uw echte werkbladen moet u het trendlijntype kiezen dat overeenkomt met uw datatype.
Belangrijke opmerking! De trendlijnformules mogen alleen worden gebruikt met XY-strooitabellen omdat alleen deze grafiek beide x en y assen als numerieke waarden. Voor meer informatie, zie Waarom Excel trendlijnvergelijking fout kan zijn.
Lineaire trendlijnvergelijking en formules
De lineaire trendlijnvergelijking gebruikt de methode van de kleinste kwadraten om de helling en onderscheppen coëfficiënten zodat:
y = bx + aWaar:
- b is de helling van een trendlijn.
- a is de y-intercept wat de verwachte gemiddelde waarde is van y wanneer alle x variabelen gelijk zijn aan 0. Op een grafiek is dat het punt waar de trendlijn de y as.
Voor lineaire regressie biedt Microsoft Excel speciale functies om de helling- en interceptcoëfficiënten te verkrijgen.
Helling van de trendlijn
b: =SLOPE(y,x)
Y-intercept
a: =INTERCEPT(y,x)
Aangenomen dat de x is B2:B13 en de y bereik C2:C13 is, gaan de reële formules als volgt:
=HELLING(C2:C13, B2:B13)
=INTERCEPT(C2:C13,B2:B13)
Dezelfde resultaten kunnen worden bereikt door de LINEST-functie te gebruiken als een matrixformule Selecteer hiervoor 2 aangrenzende cellen in dezelfde rij, voer de formule in en druk op Ctrl + Shift + Enter om deze te voltooien:
=LINEST(C2:C13,B2:B13)
Zoals in onderstaande schermafbeelding te zien is, komen de helling- en interceptcoëfficiënten die de formules opleveren perfect overeen met de coëfficiënten in de lineaire trendlijnvergelijking in de grafiek, alleen zijn deze laatste afgerond op 4 decimalen: 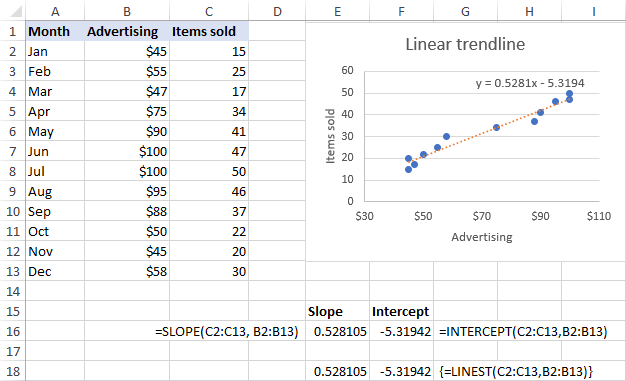
Exponentiële trendlijnvergelijking en formules
Voor de exponentiële trendlijn gebruikt Excel de volgende vergelijking:
y = aebxWaar a en b zijn berekende coëfficiënten en e is de wiskundige constante e (de basis van de natuurlijke logaritme).
De coëfficiënten kunnen worden berekend aan de hand van deze algemene formules:
a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))
b: =INDEX(LINEST(LN(y), x), 1)
Voor onze voorbeeldgegevens zien de formules er als volgt uit:
a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))
b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1) 
Logaritmische trendlijnvergelijking en formules
Hier is de logaritmische trendlijnvergelijking in Excel:
y = a*ln(x)+bWaar a en b zijn constanten en ln is de natuurlijke logaritme functie.
Om de constanten te krijgen gebruikt u deze algemene formules, die alleen verschillen in het laatste argument:
a: =INDEX(LINEST(y, LN(x)), 1)
b: =INDEX(LINEST(y, LN(x)), 1, 2)
Voor onze steekproef gebruiken wij deze:
a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)
b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2) 
Polynomiale trendlijnvergelijking en formules
Om de polynomiale trendlijn te berekenen gebruikt Excel deze vergelijking:
y = b 6 x6 + ... + b 2 x2 + b 1 x + aWaar b 1 ... b 6 en a zijn constanten.
Afhankelijk van de graad van uw polynomiale trendlijn, gebruikt u een van de volgende formules om de constanten te verkrijgen.
Kwadratische (2e orde) polynomiale trendlijn
Vergelijking: y = b 2 x2+ b 1 x + a
b 2 : =INDEX(LINEST(y, x^{1,2}), 1)
b 1 : =INDEX(LINEST(y, x^{1,2}), 1, 2)
a: =INDEX(LINEST(y, x^{1,2}), 1, 3)
Kubische (3e orde) polynomiale trendlijn
Vergelijking: y = b 3 x3 + b 2 x2+ b 1 x + a
b 3 : =INDEX(LINEST(y, x^{1,2,3}), 1)
b 2 : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)
b 1 : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)
a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)
De formules voor polynomiale trendlijnen van hogere graden kunnen worden opgebouwd door hetzelfde patroon te gebruiken.
Voor onze gegevensreeks voldoet de polynomiale trendlijn van de tweede orde beter, dus gebruiken wij deze formules:
b 2 : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)
b 1 : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)
a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3) 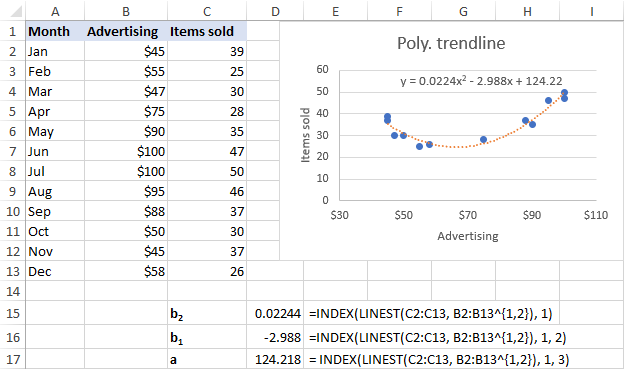
Vermogenstrendlijnvergelijking en -formules
Een vermogenstrendlijn in Excel wordt getrokken op basis van deze eenvoudige vergelijking:
y = axbWaar a en b zijn constanten, die met deze formules kunnen worden berekend:
a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))
b: =INDEX(LINEST(LN(y), LN(x),), 1)
In ons geval werken de volgende formules prima:
a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))
b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1) 
Excel trendlijnvergelijking is fout - redenen en oplossingen
Indien u denkt dat Excel een trendlijn onjuist heeft getekend of dat de in uw grafiek weergegeven trendlijnformule onjuist is, kunnen de volgende twee punten enig licht op de situatie werpen.
Excel trendlijnvergelijking is alleen correct in spreidingsdiagrammen
Excel-trendlijnformules mogen alleen worden gebruikt bij XY-grafieken (spreidingsgrafieken) omdat alleen bij dit grafiektype zowel de y-as als de x-as als numerieke waarden worden uitgezet.
In lijndiagrammen, kolom- en staafdiagrammen worden numerieke waarden alleen op de y-as uitgezet. De x-as wordt voorgesteld door een lineaire reeks (1, 2, 3,...) ongeacht of de aslabels getallen of tekst zijn. Wanneer u een trendlijn maakt in deze diagrammen, gebruikt Excel die veronderstelde x-waarden in de trendlijnformule.
Cijfers zijn afgerond in Excel trendlijnvergelijking
Om minder ruimte in de grafiek in te nemen, geeft Excel zeer weinig significante cijfers weer in een trendlijnvergelijking. Mooi van opzet, maar het vermindert de nauwkeurigheid van de formule aanzienlijk wanneer u handmatig x-waarden in de vergelijking invoert.
Een eenvoudige oplossing is om meer decimalen in de vergelijking te tonen. U kunt ook de coëfficiënten berekenen door een formule te gebruiken die overeenkomt met uw trendlijntype, en de formulecellen zo opmaken dat ze een voldoende aantal decimalen tonen. Hiervoor klikt u gewoon op de knop Verhoging Decimaal knop op de Home tabblad in de Nummer groep.
Zo kun je in Excel verschillende soorten trendlijnen maken en hun vergelijkingen krijgen. Ik dank je voor het lezen en hoop je volgende week op onze blog te zien!

