In hierdie tutoriaal vind jy die gedetailleerde beskrywing van al die tendenslynopsies wat in Excel beskikbaar is en wanneer om dit te gebruik. Jy sal ook leer hoe om 'n tendenslynvergelyking in 'n grafiek te vertoon en die helling van tendenslyn te vind.

Dit is baie maklik om 'n tendenslyn in Excel by te voeg. Die enigste werklike uitdaging is om die tendenslyntipe te kies wat die beste ooreenstem met die tipe data wat jy ontleed. In hierdie tutoriaal vind u die gedetailleerde beskrywing van al die tendenslyn-opsies wat in Excel beskikbaar is en wanneer om dit te gebruik. As jy op soek is na hoe om 'n tendenslyn in 'n Excel-grafiek in te voeg, kyk asseblief na die bogenoemde gekoppelde tutoriaal.

Excel-neigingslyntipes

Wanneer jy 'n tendenslyn in Excel byvoeg , jy het 6 verskillende opsies om van te kies. Daarbenewens maak Microsoft Excel dit moontlik om 'n tendenslynvergelyking en R-kwadraatwaarde in 'n grafiek te vertoon:

• Tendenslynvergelyking is 'n formule wat 'n lyn vind wat die beste by die datapunte pas.
• R-kwadraatwaarde meet die tendenslynbetroubaarheid - hoe nader R2 aan 1 is, hoe beter pas die tendenslyn by die data.

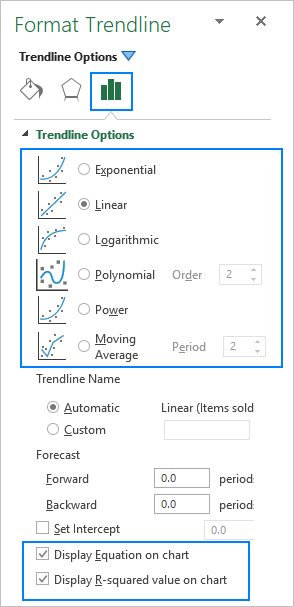
Hieronder vind jy 'n kort beskrywing van elke tendenslyntipe met grafiekvoorbeelde.

Lineêre tendenslyn

Die lineêre tendenslyn is die beste om te wees gebruik met lineêre datastelle wanneer die datapunte in 'n grafiek soos 'n reguit lyn lyk. Tipies, 'n lineêre tendenslyn beskryf 'n deurlopende styging of dalingoor tyd.

Byvoorbeeld, die volgende lineêre tendenslyn toon 'n bestendige toename in verkope oor 6 maande. En die R2-waarde van 0, =INDEX(LINEST(y, x^{1,2,3}), 1) dui op 'n redelik goeie passing van die beraamde tendenslynwaardes by die werklike data.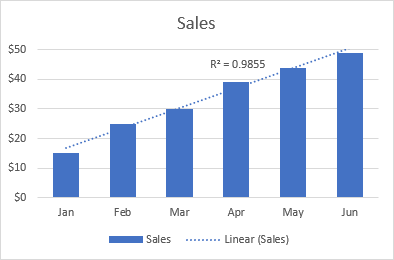

Eksponensiële tendenslyn

Die eksponensiële tendenslyn is 'n geboë lyn wat 'n styging of daling in datawaardes teen 'n toenemende tempo illustreer, daarom is die lyn gewoonlik meer geboë aan die een kant. Hierdie tendenslyntipe word dikwels in wetenskap gebruik, byvoorbeeld om 'n menslike bevolkingsgroei of afname in wildbevolkings te visualiseer.

Neem asseblief kennis dat 'n eksponensiële tendenslyn nie geskep kan word vir data wat nulle of negatiewe waardes bevat nie.

'n Goeie voorbeeld van 'n eksponensiële kurwe is die verval in die hele wilde tierbevolking op die aarde.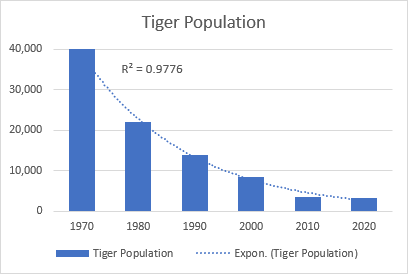

Logaritmiese tendenslyn

Die logaritmiese beste-paslyn word gewoonlik gebruik om data te plot wat vinnig toeneem of afneem en dan afplat. Dit kan beide positiewe en negatiewe waardes insluit.

'n Voorbeeld van 'n logaritmiese tendenslyn kan 'n inflasiekoers wees, wat eers hoër word, maar na 'n rukkie stabiliseer.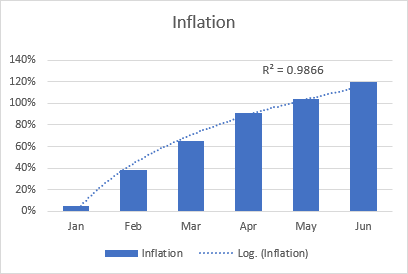

Polinoomneiginglyn

Die polinoomkrommeneiginglyn werk goed vir groot datastelle met ossillerende waardes wat meer as een styging en daling het.

Oor die algemeen word 'n polinoom geklassifiseer deur die graad van die grootste eksponent. Die graad van die polinoom tendenslyn kanword ook bepaal deur die aantal buigings op 'n grafiek. Tipies het 'n kwadratiese polinoomneigingslyn een buiging (heuwel of vallei), 'n kubieke polinoom het 1 of 2 buigings, en 'n kwadratiese polinoom het tot 3 buigings.

Wanneer 'n polinoomneiginglyn in 'n Excel-grafiek bygevoeg word, jy spesifiseer die graad deur die ooreenstemmende nommer in die Orde -blokkie op die Format Trendline -venster in te tik, wat by verstek 2 is: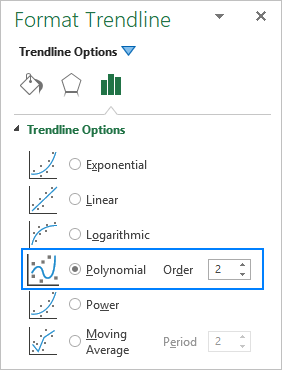

Byvoorbeeld, die kwadratiese polinoomtendens is duidelik op die volgende grafiek wat die verband tussen die wins en die aantal jare wat die produk op die mark is aandui: styg in die begin, piek in die middel en daling naby die einde.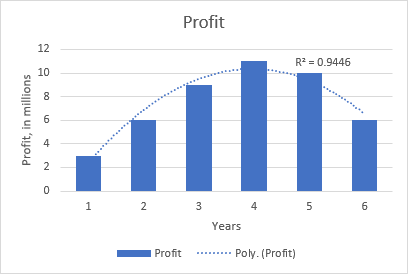

Drygtendenslyn

Die kragtendenslyn is baie soortgelyk aan die eksponensiële kurwe, net dit het 'n meer simmetriese boog. Dit word algemeen gebruik om metings te plot wat teen 'n sekere tempo toeneem.

'n Kragneigingslyn kan nie by 'n Excel-grafiek gevoeg word wat nul of negatiewe waardes bevat nie.

As 'n voorbeeld, kom ons teken 'n kragtendenslyn om die chemiese reaksietempo te visualiseer. Let op die R-kwadraatwaarde van 0,9918, wat beteken dat ons tendenslyn byna perfek by die data pas.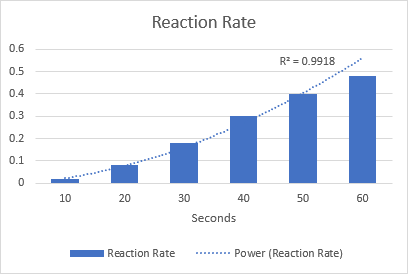

Bewegende gemiddelde tendenslyn

Wanneer die datapunte in jou grafiek baie op- en afdraandes het, kan 'n bewegende gemiddelde tendenslyn die uiterste skommelinge in datawaardes glad maak om 'n patroon duideliker te wys. Hiervoor bereken Excel diebewegende gemiddelde van die aantal periodes wat jy spesifiseer (2 by verstek) en plaas daardie gemiddelde waardes as punte in die lyn. Hoe hoër die Periode -waarde, hoe gladder die lyn.

'n Goeie praktiese voorbeeld is om die bewegende gemiddelde tendenslyn te gebruik om skommelinge in 'n aandeelprys te openbaar wat andersins moeilik sou wees om waar te neem.

Vir meer inligting, sien asseblief: Hoe om 'n bewegende gemiddelde tendenslyn by 'n Excel-grafiek te voeg.

Excel tendenslynvergelykings en formules

Hierdie afdeling beskryf die vergelykings wat Excel gebruik vir verskillende tendenslyn tipes. Jy hoef nie hierdie formules met die hand te bou nie, sê bloot vir Excel om die tendenslynvergelyking in 'n grafiek te vertoon.

Ons sal ook die formule bespreek om die helling van 'n tendenslyn en ander koëffisiënte te vind. Die formules veronderstel dat jy 2 stelle veranderlikes het: onafhanklike veranderlike x en afhanklike veranderlike y . In jou werkblaaie kan jy hierdie formules gebruik om die voorspelde y -waardes vir enige gegewe waardes van x te kry.

Vir konsekwentheid sal ons dieselfde data gebruik stel met effens wisselende waardes vir al die voorbeelde. Hou egter asseblief in gedagte dat dit slegs vir demonstrasiedoeleindes is. In jou regte werkblaaie moet jy die tendenslyntipe kies wat ooreenstem met jou datatipe.

Belangrike nota! Die tendenslynformules moet slegs met XY-verspreidingskaarte gebruik word, want slegs ditgrafiek plot beide x en y asse as numeriese waardes. Vir meer inligting, sien asseblief Hoekom Excel-neiginglynvergelyking verkeerd kan wees.

Lineêre tendenslynvergelyking en formules

Die lineêre tendenslynvergelyking gebruik die kleinste kwadrate-metodes om die helling te soek en afsnit -koëffisiënte sodanig dat:

y = bx + a

Waar:

• b die helling is van 'n tendenslyn.
• a is die y-afsnit , wat die verwagte gemiddelde waarde van y is wanneer alle x veranderlikes is gelyk aan 0. Op 'n grafiek is dit die punt waar die neiginglyn die y -as kruis.

Vir lineêre regressie verskaf Microsoft Excel spesiale funksies om die helling en snypuntkoëffisiënte.

Huinling van neiginglyn

b: =SLOPE(y,x)

Y-afsnit

a: =INTERCEPT(y,x)

As die x -reeks B2:B13 is en die y -reeks C2:C13 is, gaan die werklike formules soos volg uit:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Dieselfde resultate kan bereik word deur die LINEST-funksie as 'n skikkingformule te gebruik. Hiervoor, kies 2 aangrensende selle in dieselfde ry, voer die formule in en druk Ctrl + Shift + Enter om dit te voltooi:

=LINEST(C2:C13,B2:B13)

Soos getoon in die skermkiekie hieronder, die helling en snypunt koëffisiënte wat deur die formules teruggegee word, is perfek in lyn met die koëffisiënte in die lineêre tendenslynvergelyking wat in die grafiek vertoon word, slegs laasgenoemde word tot 4 desimale plekke afgerond: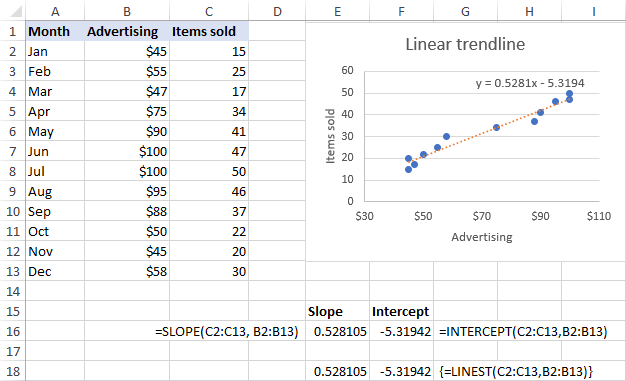

Eksponensiële tendenslynvergelyking en formules

Vir die eksponensiële tendenslyn gebruik Excel die volgende vergelyking:

y = aebx

Waar a en b is berekende koëffisiënte en e is die wiskundige konstante e (die basis van die natuurlike logaritme).

Die koëffisiënte kan bereken word deur hierdie generiese formules te gebruik:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Vir ons voorbeelddatastel neem die formules die volgende vorm aan:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logaritmiese tendenslynvergelyking en formules

Hier is die logaritmiese tendenslynvergelyking in Excel:

y = a*ln(x)+b

Waar a en b is konstantes en ln is die natuurlike logaritmefunksie.

Om die konstantes te kry, gebruik hierdie generiese formules, wat slegs in die laaste argument verskil:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Vir ons voorbeelddatastel gebruik ons ​​hierdie:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polinoomneiginglynvergelyking en formules

Om die polinoomneiginglyn uit te werk, gebruik Excel hierdie vergelyking:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Waar b ₁ ... b ₆ en a is konstantes.

Afhangende van die graad van jou polinoomneigingslyn, gebruik een van die volgende stelle formules om die konstantes te kry.

Kwadratiese (2de orde) polinoom tendenslyn

Vergelyking: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kubieke (3de orde) polinoom tendenslyn

Vergelyking: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Die formules vir hoërgraad polinoomneigingslyne kan gebou word deur dieselfde patroon te gebruik.

Vir ons datastel, die 2de orde polinoomneigingslyn suites beter, daarom gebruik ons ​​hierdie formules:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)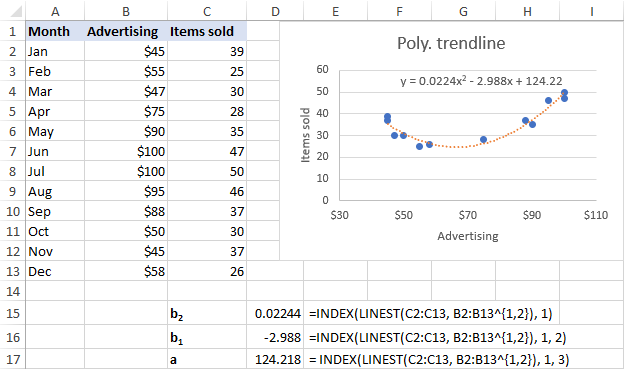

Drywingtendenslynvergelyking en formules

'n Kragneigingslyn in Excel word geteken op grond van hierdie eenvoudige vergelyking:

y = axb

Waar a en b is konstantes, wat met hierdie formules bereken kan word:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

In ons geval werk die volgende formules 'n lekkerte :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Excel tendenslynvergelyking is verkeerd - redes en regstellings

As jy dink dat Excel 'n tendenslyn verkeerd geteken het of die tendenslynformule wat in jou grafiek vertoon word, verkeerd is, kan die volgende twee punte 'n bietjie verloor lig op die situasie.

Excel-neiginglynvergelyking is slegs korrek in spreidingsgrafieke

Excel-neiginglynformules moet slegs met XY (verstrooiings)grafieke gebruik word, want slegs in hierdie grafiek tik beide die y-as in en x-as word as numeriese waardes geplot.

In lyngrafieke, kolom- en staafgrafieke word numeriese waardes slegs op die y-as geplot. Die x-as word voorgestel deur 'n lineêre reeks (1, 2,3,...) ongeag of die as-byskrifte getalle of teks is. Wanneer jy 'n neiginglyn in hierdie grafieke maak, gebruik Excel daardie veronderstelde x-waardes in die tendenslynformule.

Getal is afgerond in Excel-neiginglynvergelyking

Om minder spasie in die grafiek in te neem, vertoon Excel baie min betekenisvolle syfers in 'n tendenslynvergelyking. Mooi in terme van ontwerp, dit verminder die formule se akkuraatheid aansienlik wanneer jy handmatig x waardes in die vergelyking verskaf.

'n Maklike oplossing is om meer desimale plekke in die vergelyking te wys. Alternatiewelik kan jy die koëffisiënte bereken deur 'n formule te gebruik wat ooreenstem met jou tendenslyntipe, en die formuleselle formateer sodat hulle 'n voldoende aantal desimale plekke toon. Hiervoor klik eenvoudig die Verhoog desimale -knoppie op die Tuis -oortjie in die Getal -groep.

Dis hoe jy verskillende tendenslyntipes kan maak in Excel en kry hul vergelykings. Ek bedank jou vir die lees en hoop om jou volgende week op ons blog te sien!