Энэ зааварт та Excel-д байгаа чиг хандлагын бүх сонголтууд болон тэдгээрийг хэзээ ашиглах талаар дэлгэрэнгүй тайлбарыг олох болно. Мөн та трендийн шугамын тэгшитгэлийг диаграммд харуулах, чиг хандлагын налууг хэрхэн олох талаар сурах болно.

Excel дээр тренд шугам нэмэхэд маш хялбар байдаг. Цорын ганц сорилт бол таны дүн шинжилгээ хийж буй өгөгдлийн төрөлд хамгийн сайн тохирох чиг хандлагын төрлийг сонгох явдал юм. Энэхүү гарын авлагад та Excel-д байгаа чиг хандлагын бүх сонголтууд болон тэдгээрийг хэзээ ашиглах талаар дэлгэрэнгүй тайлбарыг олох болно. Хэрэв та Excel-ийн диаграммд чиг хандлагын шугамыг хэрхэн оруулахыг хайж байгаа бол дээрх холбоос бүхий зааварчилгааг үзнэ үү.

Excel-ийн чиг хандлагын төрлүүд

Excel дээр тренд шугам нэмэх үед , танд 6 өөр сонголт байна. Нэмж дурдахад Microsoft Excel нь чиг хандлагын тэгшитгэл болон R квадрат утгыг графикт харуулах боломжийг олгодог:

• Тренд шугамын тэгшитгэл нь өгөгдлийн цэгүүдэд хамгийн сайн тохирох мөрийг олох томьёо юм.
• R-квадрат утга нь чиг хандлагын шугамын найдвартай байдлыг хэмждэг - R2 нь 1-д ойр байх тусам чиг хандлагын шугам өгөгдөлд илүү сайн нийцдэг.

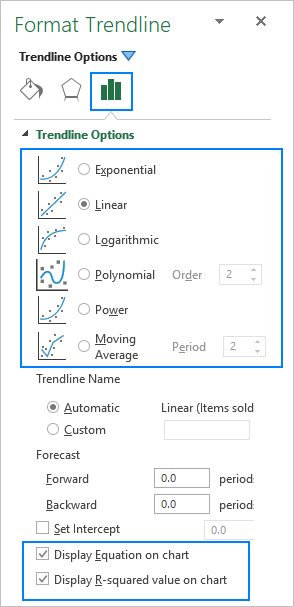
Доор та тренд шугамын төрөл бүрийн товч тайлбарыг диаграмын жишээнүүдийн хамт олох болно.

Шугаман трендийн шугам

Шугаман чиг хандлагын шугам нь хамгийн тохиромжтой. Диаграм дахь өгөгдлийн цэгүүд шулуун шугамтай төстэй үед шугаман өгөгдлийн багцад ашиглагддаг. Ерөнхийдөө шугаман чиг хандлага нь тасралтгүй өсөлт эсвэл уналтыг тодорхойлдогцаг хугацааны явцад.

Жишээ нь, дараах шугаман чиг хандлага нь 6 сарын хугацаанд борлуулалтын тогтвортой өсөлтийг харуулж байна. Мөн R2 утга нь 0.9855 нь тооцоолсон чиг хандлагын утгуудын бодит өгөгдөлтэй нэлээд сайн тохирч байгааг харуулж байна.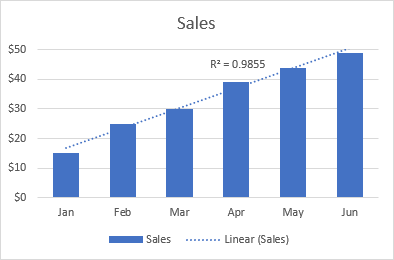

Экспоненциал чиг хандлагын шугам

Экспоненциал чиг хандлагын шугам нь өгөгдлийн үнэ цэнэ өсөх хурдаар нэмэгдэж эсвэл буурч байгааг харуулсан муруй шугам тул шугам нь ихэвчлэн нэг талдаа илүү муруй байдаг. Энэ чиг хандлагын шугамын төрлийг шинжлэх ухаанд ихэвчлэн ашигладаг, тухайлбал хүний ​​популяцийн өсөлт, бууралтыг төсөөлөхөд ашигладаг.

Тэг эсвэл сөрөг утгатай өгөгдөлд экспоненциал чиг хандлагын шугам үүсгэх боломжгүй гэдгийг анхаарна уу.

Экспоненциал муруйны сайн жишээ бол дэлхий дээрх зэрлэг барын популяцийг бүхэлд нь задрах явдал юм.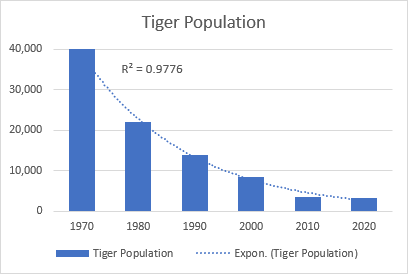

Логарифмын чиг хандлагын шугам

Логарифмын хамгийн тохиромжтой шугамыг ерөнхийдөө хурдан нэмэгдэж эсвэл буурч, дараа нь тэгшлэх өгөгдлийг зурахад ашигладаг. Үүнд эерэг ба сөрөг утгыг хоёуланг нь багтааж болно.

Логарифмын чиг хандлагын жишээ нь эхлээд өсөж байгаа боловч хэсэг хугацааны дараа тогтворждог инфляцийн түвшин байж болно.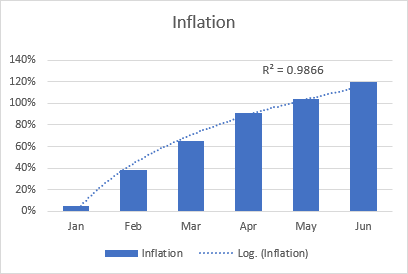

Олон гишүүнт чиг хандлагын шугам

Олон гишүүнт муруй шугам нь нэгээс олон өсөлт бууралттай хэлбэлзэх утгатай том өгөгдлийн багцад сайн ажилладаг.

Ерөнхийдөө олон гишүүнтийг дараах байдлаар ангилдаг. хамгийн том экспонентийн зэрэг. Олон гишүүнт тренд шугамын зэрэг болномөн график дээрх гулзайлтын тоогоор тодорхойлогдоно. Ер нь квадрат олон гишүүнт чиг хандлагын шугам нь нэг гулзайлттай (толгой эсвэл хөндий), куб олон гишүүнт 1 эсвэл 2 гулзайлттай, дөрвөлжин олон гишүүнт 3 хүртэл нугалж байна.

Excel графикт олон гишүүнт чиг хандлагын шугам нэмэх үед, та Тренд шугамыг форматлах самбар дээрх Захиалга нүдэнд харгалзах тоог бичиж, зэрэглэлийг зааж өгөх бөгөөд энэ нь анхдагчаар 2 байна: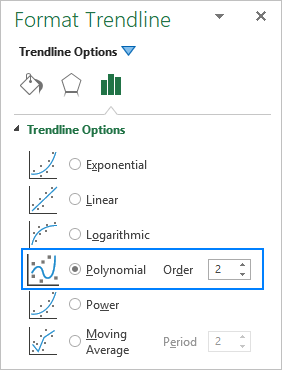

Жишээ нь, квадрат олон гишүүнт хандлага ашиг болон бүтээгдэхүүний зах зээл дээр байсан жилийн тоо хоорондын хамаарлыг харуулсан дараах график дээр илт харагдаж байна: эхэнд нь өсөлт, дунд нь оргил, төгсгөлд нь буурч байна.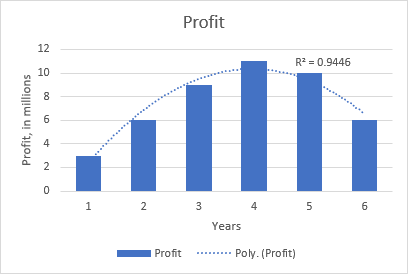

Эрчим хүчний чиг хандлагын шугам

Эрчим хүчний чиг хандлагын шугам нь экспоненциал муруйтай маш төстэй, зөвхөн илүү тэгш хэмтэй нумтай. Энэ нь тодорхой хурдацтай өсөх хэмжилтийг зурахад ихэвчлэн ашиглагддаг.

Тэг эсвэл сөрөг утгатай Excel диаграмд ​​чадлын чиг хандлагын шугамыг нэмэх боломжгүй.

Жишээ нь: химийн урвалын хурдыг дүрслэхийн тулд эрчим хүчний чиг хандлагын шугам. R-squared утгыг анхаарна уу 0.9918, энэ нь бидний чиг хандлага өгөгдөлд бараг төгс нийцэж байна гэсэн үг юм.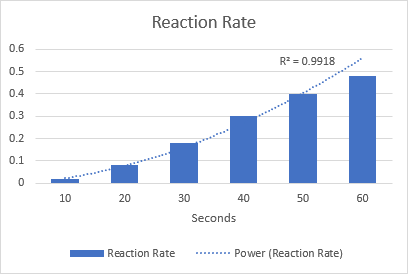

Хөдөлгөөнт дундаж чиг хандлагын шугам

Таны диаграм дахь өгөгдлийн цэгүүд олон тооны өсөлт, бууралттай үед хөдөлгөөнт дундаж тренд шугам нь өгөгдлийн утгын хэт хэлбэлзлийг зөөлрүүлж, загварыг илүү тодорхой харуулах боломжтой. Үүний тулд Excel тооцоолнотаны зааж буй үеүүдийн тооны хөдөлгөөнт дундаж (анхдагчаар 2) бөгөөд тэдгээр дундаж утгыг мөрөнд цэг болгон оруулна. Үеийн утга өндөр байх тусам шугам илүү жигд болно.

Хөдөлгөөнт дундаж трэнд шугамыг ашиглан хувьцааны үнийн хэлбэлзлийг илрүүлэх, өөрөөр хэлбэл ажиглахад хэцүү байх болно.

Дэлгэрэнгүй мэдээллийг: Excel-ийн графикт хөдөлж буй дундаж чиг хандлагын шугамыг хэрхэн нэмэх талаар үзнэ үү.

Excel-ийн чиг хандлагын тэгшитгэл ба томьёо

Энэ хэсэгт Excel-ийн ашигладаг тэгшитгэлүүдийг тайлбарласан болно. янз бүрийн чиг хандлагын төрөлд зориулагдсан. Та эдгээр томьёог гараар бүтээх шаардлагагүй, зүгээр л Excel-д тренд шугамын тэгшитгэлийг графикт харуулахыг хэлээрэй.

Мөн бид тренд шугамын налуу болон бусад коэффициентүүдийг олох томъёоны талаар ярилцах болно. Томъёо нь танд 2 багц хувьсагч байгаа гэж үздэг: бие даасан хувьсагч x ба хамааралтай хувьсагч y . Та ажлын хуудсандаа эдгээр томьёог ашиглан x -н өгөгдсөн аливаа утгуудын таамагласан y утгыг авах боломжтой.

Тогтвортой байхын тулд бид ижил өгөгдлийг ашиглана. бүх жишээн дээр бага зэрэг өөр утгатай тохируулна. Гэсэн хэдий ч энэ нь зөвхөн үзүүлэх зорилготой гэдгийг санаарай. Бодит ажлын хуудсууд дээрээ та өгөгдлийн төрөлдөө тохирох тренд шугамын төрлийг сонгох хэрэгтэй.

Анхаарах зүйл! Тренд шугамын томьёог зөвхөн XY тараах графиктай ашиглах ёстой, учир нь зөвхөн энэдиаграмм нь x ба y тэнхлэгүүдийг хоёуланг нь тоон утга болгон зурдаг. Дэлгэрэнгүй мэдээллийг Excel чиг хандлагын тэгшитгэл яагаад буруу байж болох талаар үзнэ үү.

Шугаман чиг хандлагын тэгшитгэл ба томьёо

Шугаман чиг хандлагын тэгшитгэл нь налууг хайхдаа хамгийн бага квадратын аргыг ашигладаг. ба хэсэглэх коэффициентүүд нь:

y = bx + a

Үүнд:

• b нь налуу юм. чиг хандлагын шугамын.
• a нь y-таслалт бөгөөд энэ нь бүх x<үед y -ийн хүлээгдэж буй дундаж утга юм. 2> хувьсагч нь 0-тэй тэнцүү байна. График дээр энэ нь чиг хандлагын шугам нь y тэнхлэгийг огтолж буй цэг юм.

Шугаман регрессийн хувьд Microsoft Excel нь тусгай функцээр хангадаг. налуу ба огтлолцлын коэффициент.

Тренд шугамын налуу

b: =SLOPE(y,x)

Y- огтлолцол

a: =INTERCEPT(y,x)

x мужийг B2:B13, y мужийг C2:C13 гэж үзвэл бодит амьдрал дээрх томьёо дараах байдалтай байна:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

ШУГРАН функцийг массивийн томьёо болгон ашигласнаар ижил үр дүнд хүрч болно. Үүний тулд нэг мөрөнд зэргэлдээх 2 нүдийг сонгоод томьёо оруулаад Ctrl + Shift + Enter дарж дуусгана уу:

=LINEST(C2:C13,B2:B13)

Доорх дэлгэцийн агшинд үзүүлсэн шиг налуу ба огтлолцол Томъёогоор буцаасан коэффициентүүд нь диаграммд үзүүлсэн шугаман чиг хандлагын тэгшитгэлийн коэффициентүүдтэй төгс нийцэж байгаа бөгөөд зөвхөн сүүлийнх нь аравтын бутархайн 4 орон хүртэл дугуйрсан байна: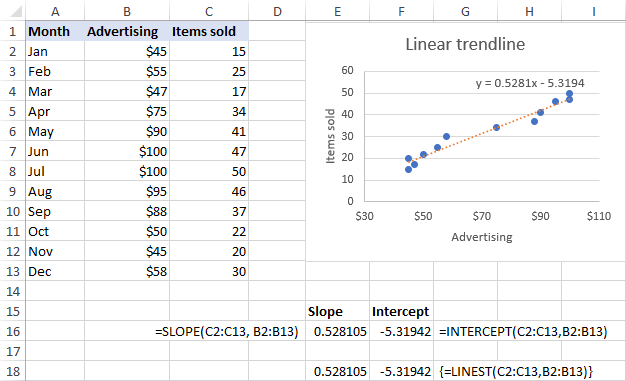

Экспоненциал чиг хандлагын тэгшитгэл ба томьёо

Экспоненциал чиг хандлагын шугамын хувьд Excel дараах тэгшитгэлийг ашигладаг:

y = aebx

Энд a ба b нь тооцоолсон коэффициентууд бөгөөд e нь математикийн тогтмол e (натурал логарифмын суурь) юм.

Итгэлцүүрүүдийг дараах ерөнхий томъёог ашиглан тооцоолж болно:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Манай түүвэр өгөгдлийн багцын хувьд томъёонууд дараах хэлбэртэй байна:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Логарифмын чиг хандлагын шугамын тэгшитгэл ба томьёо

Эхселийн логарифмын чиг хандлагын тэгшитгэл энд байна:

y = a*ln(x)+b

Энд a ба b нь тогтмол ба ln нь натурал логарифмын функц юм.

Тогтмол утгыг авахын тулд зөвхөн сүүлийн аргумент дээр ялгаатай эдгээр ерөнхий томъёог ашиглана уу:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Бид түүвэр өгөгдлийн багцын хувьд эдгээрийг ашигладаг:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Олон гишүүнт чиг хандлагын шугамын тэгшитгэл ба томьёо

Олон гишүүнт чиг хандлагын шугамыг боловсруулахын тулд Excel нь дараах тэгшитгэлийг ашигладаг:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Энд b ₁ … b ₆ ба a нь тогтмол байна.

Таны олон гишүүнт чиг хандлагын зэргээс хамааран дараах багц томъёоны аль нэгийг ашиглана уу. тогтмолуудыг авна.

Квадрат (2-р эрэмбийн) олон гишүүнт тренд шугам

Тэгшитгэл: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

б ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Куб (3-р эрэмбийн) олон гишүүнт тренд шугам

Тэгшитгэл: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Дээд зэргийн олон гишүүнт чиг хандлагын шугамын томъёог ижил хэв маягаар барьж болно.

Манай өгөгдлийн багцын хувьд 2-р эрэмбийн олон гишүүнт чиг хандлагын шугамын багцууд. илүү сайн, тиймээс бид эдгээр томъёог ашиглаж байна:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)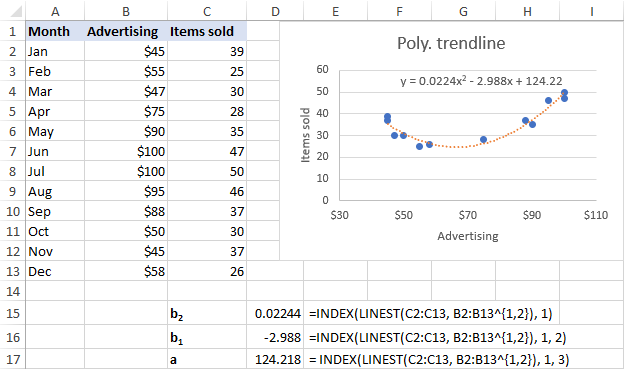

Цахилгааны чиг хандлагын тэгшитгэл ба томьёо

Эксель дээрх чадлын чиг хандлагын шугамыг дараах энгийн тэгшитгэл дээр үндэслэн зурсан:

y = axb

Энд a ба b нь тогтмолууд бөгөөд эдгээрийг дараах томъёогоор тооцоолж болно:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

Манай тохиолдолд дараах томъѐо нь энгийн байдлаар ажилладаг. :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Excel-ийн чиг хандлагын тэгшитгэл буруу байна - шалтгаан ба засварууд

Хэрэв та Excel чиг хандлагын шугамыг буруу зурсан гэж бодож байвал эсвэл таны диаграммд харуулсан чиг хандлагын томъёо буруу байвал дараах хоёр цэг зарим зүйлийг алдаж болзошгүй нөхцөл байдлыг тодруулна.

Excel-ийн чиг хандлагын тэгшитгэл нь зөвхөн тараах диаграмд ​​зөв байна

Excel-ийн чиг хандлагын томъёог зөвхөн XY (тараа) графиктай ашиглах ёстой, учир нь зөвхөн энэ диаграммд у тэнхлэгийг хоёуланг нь бичнэ. ба х тэнхлэгийг тоон утга болгон зурна.

Мөрийн диаграм, багана, багана графикт тоон утгыг зөвхөн у тэнхлэгт зурна. X тэнхлэгийг шугаман цуваагаар (1, 2,3,…) тэнхлэгийн шошго нь тоо эсвэл текст байхаас үл хамааран. Таныг эдгээр диаграммд чиг хандлагын шугам үүсгэх үед Excel нь трендийн шугамын томъёонд тэдгээр таамагласан x утгуудыг ашигладаг.

Excel-ийн чиг хандлагын тэгшитгэлд тоонуудыг дугуйрсан байна

Диаграммд бага зай эзлэхийн тулд Excel харуулдаг. тренд шугамын тэгшитгэлд маш цөөхөн чухал цифрүүд. Загварын хувьд сайн, энэ нь тэгшитгэлд x утгыг гараар оруулахад томьёоны нарийвчлалыг мэдэгдэхүйц бууруулдаг.

Тэгшитгэлд аравтын бутархайг илүү харуулах нь хялбар засвар юм. Эсвэл та чиг хандлагын шугамын төрөлд тохирох томъёог ашиглан коэффициентийг тооцоолж, томьёоны нүднүүдийг хангалттай тооны аравтын орон харуулахаар форматлаж болно. Үүнийг хийхийн тулд Тоо бүлгийн Нүүр таб дээрх Аравтын тоог нэмэгдүүлэх товчийг дарахад л хангалттай.

Ингэж та янз бүрийн чиг хандлагын төрлийг үүсгэж болно. Excel-д оруулаад тэгшитгэлээ авна уу. Уншиж байгаад баярлалаа, дараа долоо хоногт манай блог дээр уулзана гэж найдаж байна!