En este tutorial, encontrará una descripción detallada de todas las opciones de línea de tendencia disponibles en Excel y cuándo utilizarlas. También aprenderá a mostrar una ecuación de línea de tendencia en un gráfico y a encontrar la pendiente de la línea de tendencia.

Es muy fácil añadir una línea de tendencia en Excel. El único desafío real es elegir el tipo de línea de tendencia que mejor se corresponda con el tipo de datos que está analizando. En este tutorial, encontrará la descripción detallada de todas las opciones de líneas de tendencia disponibles en Excel y cuándo utilizarlas. Si está buscando cómo insertar una línea de tendencia en un gráfico de Excel, consulte el tutorial enlazado anteriormente.

Tipos de líneas de tendencia en Excel

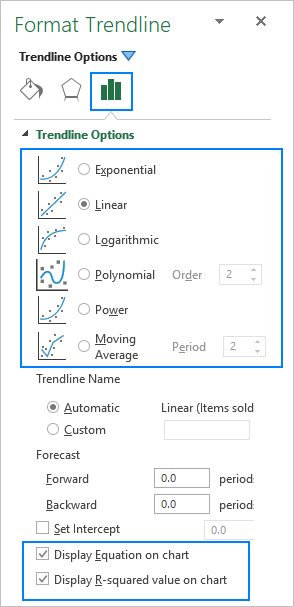
Al añadir una línea de tendencia en Excel, dispone de 6 opciones diferentes entre las que elegir. Además, Microsoft Excel permite mostrar una ecuación de línea de tendencia y el valor R-cuadrado en un gráfico:

• Ecuación de la línea de tendencia es una fórmula que encuentra la recta que mejor se ajusta a los puntos de datos.
• Valor R-cuadrado mide la fiabilidad de la línea de tendencia: cuanto más se acerque R2 a 1, mejor se ajustará la línea de tendencia a los datos.

A continuación, encontrará una breve descripción de cada tipo de línea de tendencia con ejemplos de gráficos.

Línea de tendencia lineal

La línea de tendencia lineal se utiliza mejor con conjuntos de datos lineales cuando los puntos de datos de un gráfico se asemejan a una línea recta. Normalmente, una línea de tendencia lineal describe una subida o bajada continua a lo largo del tiempo.

Por ejemplo, la siguiente línea de tendencia lineal muestra un aumento constante de las ventas a lo largo de 6 meses. Y el valor R2 de 0,9855 indica un ajuste bastante bueno de los valores estimados de la línea de tendencia a los datos reales.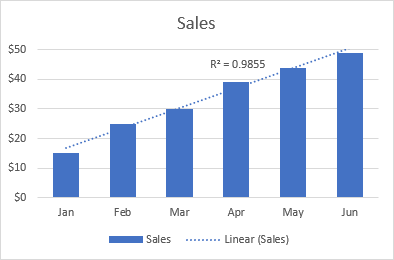

Línea de tendencia exponencial

La línea de tendencia exponencial es una línea curva que ilustra un aumento o disminución de los valores de los datos a un ritmo creciente, por lo que la línea suele ser más curva en uno de sus lados. Este tipo de línea de tendencia se utiliza a menudo en ciencias, por ejemplo, para visualizar el crecimiento de una población humana o la disminución de las poblaciones de animales salvajes.

Tenga en cuenta que no se puede crear una línea de tendencia exponencial para datos que contengan ceros o valores negativos.

Un buen ejemplo de curva exponencial es la disminución de toda la población de tigres salvajes de la Tierra.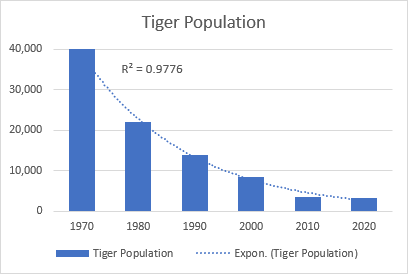

Línea de tendencia logarítmica

La línea logarítmica de mejor ajuste se utiliza generalmente para representar datos que aumentan o disminuyen rápidamente y luego se nivelan. Puede incluir valores positivos y negativos.

Un ejemplo de línea de tendencia logarítmica puede ser una tasa de inflación, que primero aumenta pero después se estabiliza.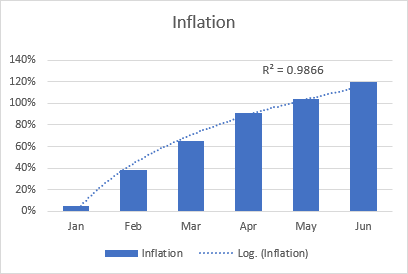

Línea de tendencia polinómica

La línea de tendencia polinómica curvilínea funciona bien para grandes conjuntos de datos con valores oscilantes que tienen más de una subida y bajada.

Generalmente, un polinomio se clasifica por el grado del exponente mayor. El grado de la línea de tendencia polinómica también puede determinarse por el número de curvas de un gráfico. Normalmente, una línea de tendencia polinómica cuadrática tiene una curva (colina o valle), un polinomio cúbico tiene 1 ó 2 curvas, y un polinomio cuártico tiene hasta 3 curvas.

Al añadir una línea de tendencia polinómica en un gráfico de Excel, se especifica el grado escribiendo el número correspondiente en el campo Pida en la casilla Formato Línea de tendencia que es 2 por defecto: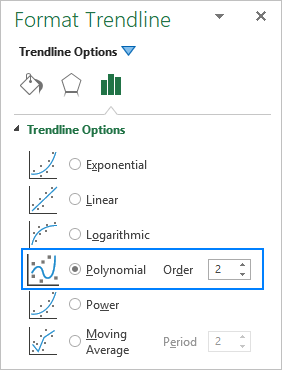

Por ejemplo, la tendencia polinómica cuadrática es evidente en el siguiente gráfico que muestra la relación entre el beneficio y el número de años que el producto lleva en el mercado: subida al principio, pico en la mitad y caída cerca del final.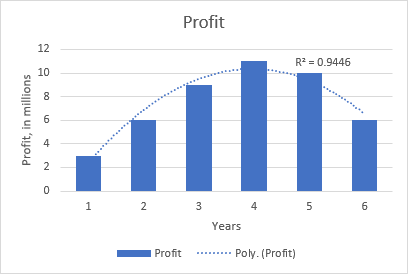

Tendencia de potencia

La línea de tendencia de la potencia es muy parecida a la curva exponencial, sólo que tiene un arco más simétrico. Se suele utilizar para trazar medidas que aumentan a un ritmo determinado.

No se puede añadir una línea de tendencia de potencia a un gráfico de Excel que contenga valores cero o negativos.

Como ejemplo, dibujemos una línea de tendencia de potencia para visualizar la velocidad de reacción química. Observe el valor R-cuadrado de 0,9918, lo que significa que nuestra línea de tendencia se ajusta a los datos casi a la perfección.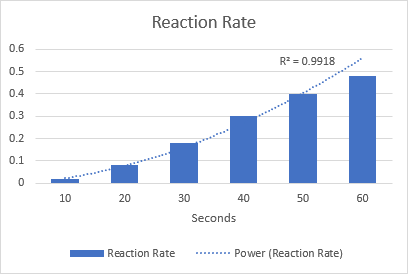

Línea de tendencia de la media móvil

Cuando los puntos de datos de su gráfico tienen muchos altibajos, una línea de tendencia de media móvil puede suavizar las fluctuaciones extremas de los valores de los datos para mostrar un patrón con mayor claridad. Para ello, Excel calcula la media móvil del número de períodos que especifique (2 por defecto) y coloca esos valores medios como puntos de la línea. Cuanto mayor sea la Periodo más suave será la línea.

Un buen ejemplo práctico es utilizar la línea de tendencia de la media móvil para revelar fluctuaciones en el precio de una acción que, de otro modo, serían difíciles de observar.

Para más información, consulte: Cómo añadir una línea de tendencia de media móvil a un gráfico de Excel.

Ecuaciones y fórmulas de líneas de tendencia en Excel

En esta sección se describen las ecuaciones que utiliza Excel para los distintos tipos de líneas de tendencia. No es necesario construir estas fórmulas manualmente, basta con decirle a Excel que muestre la ecuación de la línea de tendencia en un gráfico.

También discutiremos la fórmula para encontrar la pendiente de una línea de tendencia y otros coeficientes. Las fórmulas asumen que tienes 2 conjuntos de variables: variable independiente x y variable dependiente y En sus hojas de cálculo, puede utilizar estas fórmulas para obtener la predicción. y para cualquier valor de x .

Para mantener la coherencia, utilizaremos el mismo conjunto de datos con valores ligeramente diferentes para todos los ejemplos. Sin embargo, tenga en cuenta que es sólo para fines de demostración. En sus hojas de trabajo reales, debe elegir el tipo de línea de tendencia correspondiente a su tipo de datos.

Nota importante: las fórmulas de línea de tendencia sólo deben utilizarse con Gráficos de dispersión XY porque sólo este gráfico traza ambos x y y Para obtener más información, consulte Por qué la ecuación de línea de tendencia de Excel puede ser incorrecta.

Ecuación y fórmulas de la línea de tendencia lineal

La ecuación de la línea de tendencia lineal utiliza los métodos de mínimos cuadrados para buscar el pendiente y interceptar coeficientes tales que:

Dónde:

• b es el pendiente de una línea de tendencia.
• a es el intersección y que es el valor medio esperado de y cuando todos x variables son iguales a 0. En un gráfico, es el punto donde la línea de tendencia cruza el y eje.

Para la regresión lineal, Microsoft Excel proporciona funciones especiales para obtener los coeficientes de pendiente e intercepción.

Pendiente de la línea de tendencia

b: =SLOPE(y,x)

Intercepto Y

a: =INTERCEPT(y,x)

Suponiendo que el x es B2:B13 y el y es C2:C13, las fórmulas reales son las siguientes:

=PENDIENTE(C2:C13, B2:B13)

=INTERCEPTO(C2:C13,B2:B13)

Se pueden obtener los mismos resultados utilizando la función LINEST como un fórmula de matriz Para ello, selecciona 2 celdas adyacentes en la misma fila, introduce la fórmula y pulsa Ctrl + Mayús + Intro para completarla:

=LINEST(C2:C13,B2:B13)

Como se muestra en la siguiente captura de pantalla, los coeficientes de pendiente e intercepto devueltos por las fórmulas coinciden perfectamente con los coeficientes de la ecuación de la línea de tendencia lineal mostrada en el gráfico, sólo que estos últimos están redondeados a 4 decimales: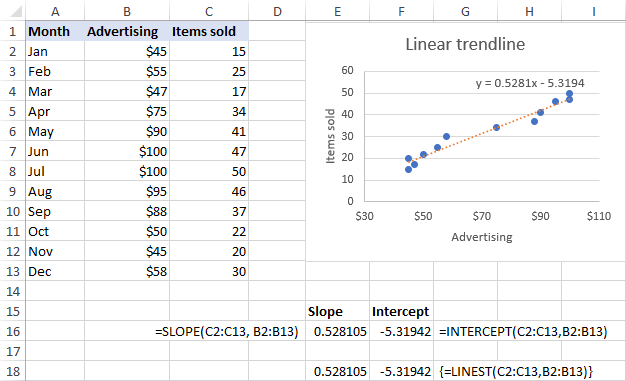

Ecuación y fórmulas de la línea de tendencia exponencial

Para la línea de tendencia exponencial, Excel utiliza la siguiente ecuación:

Dónde a y b son coeficientes calculados y e es la constante matemática e (la base del logaritmo natural).

Los coeficientes pueden calcularse utilizando estas fórmulas genéricas:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Para nuestro conjunto de datos de muestra, las fórmulas adoptan la forma siguiente:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Ecuación y fórmulas de la línea de tendencia logarítmica

Aquí está la ecuación de la línea de tendencia logarítmica en Excel:

Dónde a y b son constantes y ln es la función logaritmo natural.

Para obtener las constantes, utiliza estas fórmulas genéricas, que sólo difieren en el último argumento:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Para nuestro conjunto de datos de muestra, utilizamos estos:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Ecuación y fórmulas de la línea de tendencia polinómica

Para calcular la línea de tendencia polinómica, Excel utiliza esta ecuación:

Dónde b ₁ ... b ₆ y a son constantes.

Dependiendo del grado de tu línea de tendencia polinómica, utiliza uno de los siguientes conjuntos de fórmulas para obtener las constantes.

Línea de tendencia polinómica cuadrática (2º orden)

Ecuación: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Línea de tendencia polinómica cúbica (3er orden)

Ecuación: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3})), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3})), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3})), 1, 4)

Las fórmulas para líneas de tendencia polinómicas de grado superior pueden construirse utilizando el mismo patrón.

Para nuestro conjunto de datos, la línea de tendencia polinómica de 2º orden se ajusta mejor, por lo que utilizamos estas fórmulas:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)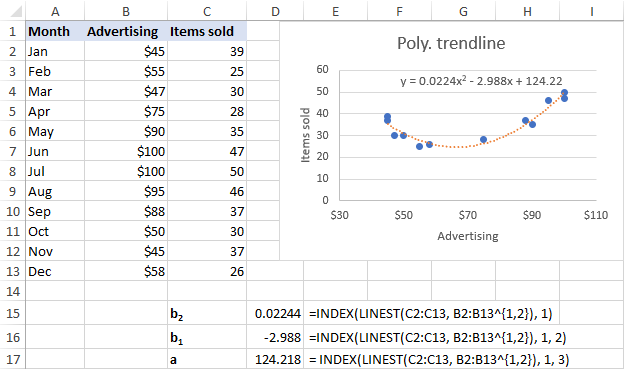

Ecuación y fórmulas de la línea de tendencia de potencia

Una línea de tendencia de potencia en Excel se dibuja basándose en esta sencilla ecuación:

Dónde a y b son constantes, que pueden calcularse con estas fórmulas:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

En nuestro caso, las siguientes fórmulas funcionan de maravilla:

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

La ecuación de la línea de tendencia de Excel es incorrecta - razones y soluciones

Si cree que Excel ha dibujado mal una línea de tendencia o que la fórmula de la línea de tendencia que aparece en su gráfico es incorrecta, los dos puntos siguientes pueden arrojar algo de luz sobre la situación.

La ecuación de la línea de tendencia de Excel sólo es correcta en los gráficos de dispersión

Las fórmulas de líneas de tendencia de Excel sólo deben utilizarse con gráficos XY (de dispersión) porque sólo en este tipo de gráfico tanto el eje y como el eje x se representan como valores numéricos.

En los gráficos de líneas, columnas y barras, los valores numéricos se representan sólo en el eje y. El eje x se representa mediante una serie lineal (1, 2, 3,...) independientemente de si las etiquetas de los ejes son números o texto. Cuando se hace una línea de tendencia en estos gráficos, Excel utiliza esos valores x supuestos en la fórmula de la línea de tendencia.

Los números se redondean en la ecuación de tendencia de Excel

Para ocupar menos espacio en el gráfico, Excel muestra muy pocos dígitos significativos en una ecuación de línea de tendencia. Agradable en términos de diseño, reduce significativamente la precisión de la fórmula cuando se suministran manualmente los valores x en la ecuación.

Como alternativa, puede calcular los coeficientes utilizando una fórmula correspondiente a su tipo de línea de tendencia y formatear las celdas de la fórmula para que muestren un número suficiente de decimales. Para ello, simplemente haga clic en el botón Aumentar decimal en el botón Inicio en la pestaña Número grupo.

Así es como puedes hacer diferentes tipos de líneas de tendencia en Excel y obtener sus ecuaciones. Te doy las gracias por leer y ¡espero verte en nuestro blog la semana que viene!