Šajā pamācībā jūs atradīsiet detalizētu aprakstu par visām Excel programmā pieejamajām tendenču līnijas iespējām un to izmantošanas gadījumiem. Jūs arī uzzināsiet, kā attēlot tendenču līnijas vienādojumu diagrammā un atrast tendenču līnijas slīpumu.

Ir ļoti viegli pievienot tendenču līniju programmā Excel. Vienīgais īstais izaicinājums ir izvēlēties tendenču līnijas veidu, kas vislabāk atbilst analizējamo datu veidam. Šajā pamācībā atradīsiet detalizētu aprakstu par visām programmā Excel pieejamajām tendenču līnijas iespējām un to, kad tās izmantot. Ja meklējat, kā ievietot tendenču līniju Excel diagrammā, lūdzu, skatiet iepriekš minēto saistīto pamācību.

Excel tendenču līniju veidi

Pievienojot tendenču līniju programmā Excel, varat izvēlēties no 6 dažādām iespējām. Turklāt Microsoft Excel ļauj attēlot tendenču līnijas vienādojumu un R kvadrāta vērtību diagrammā:

• Trendlīnijas vienādojums ir formula, kas atrod līniju, kura vislabāk atbilst datu punktiem.
• R-kvadrāta vērtība mēra tendences līnijas ticamību - jo tuvāk R2 ir 1, jo labāk tendences līnija atbilst datiem.

Zemāk, Jūs atradīsiet īsu aprakstu par katru trendline tipa ar diagrammas piemēriem.

Lineārā līnija

Lineāro tendences līniju vislabāk izmantot lineāru datu kopām, ja datu punkti diagrammā atgādina taisnu līniju. Parasti lineārā tendences līnija raksturo nepārtrauktu kāpumu vai kritumu laika gaitā.

Piemēram, šāda lineārā tendences līnija parāda vienmērīgu pārdošanas apjoma pieaugumu 6 mēnešu laikā. R2 vērtība 0,9855 norāda uz diezgan labu aplēsto tendences līnijas vērtību atbilstību faktiskajiem datiem.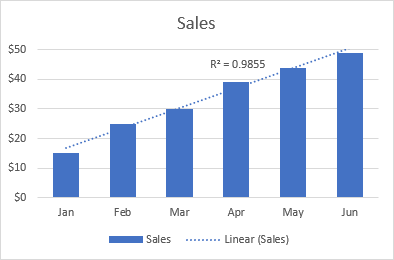

Eksponenciālā līnija

Eksponenciālā tendences līnija ir izliekta līnija, kas ilustrē datu vērtību pieaugumu vai kritumu ar pieaugošu ātrumu, tāpēc parasti līnija vienā pusē ir vairāk izliekta. Šo tendenču līnijas veidu bieži izmanto zinātnēs, piemēram, lai vizualizētu cilvēku populācijas pieaugumu vai savvaļas dzīvnieku populācijas samazināšanos.

Lūdzu, ņemiet vērā, ka eksponenciālo tendenču līniju nevar izveidot datiem, kas satur nulles vai negatīvas vērtības.

Labs eksponenciālas līknes piemērs ir visas savvaļas tīģeru populācijas samazināšanās uz Zemes.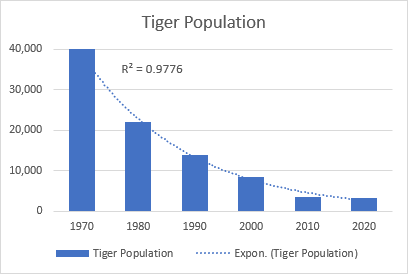

Logaritmiskā līnija

Logaritmisko vispiemērotāko līniju parasti izmanto, lai attēlotu datus, kas strauji palielinās vai samazinās un pēc tam izlīdzinās. Tajā var būt gan pozitīvas, gan negatīvas vērtības.

Logaritmiskas tendences līnijas piemērs var būt inflācijas līmenis, kas vispirms pieaug, bet pēc kāda laika stabilizējas.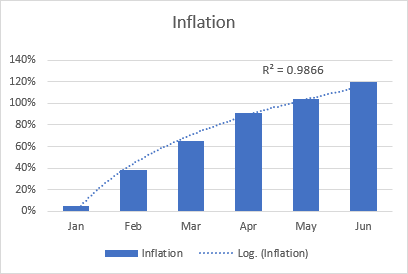

Polinoma tendences līnija

Polinomiski izliektā līknes līknes līkne labi darbojas lielām datu kopām ar svārstīgām vērtībām, kurām ir vairāk nekā viens kāpums un kritums.

Parasti polinomu klasificē pēc lielākā eksponentā pakāpes. Polinoma tendenču līnijas pakāpi var noteikt arī pēc līkumu skaita grafikā. Parasti kvadrātveida polinoma tendenču līnijai ir viens līkums (kalns vai ieleja), kubiskajam polinomam ir 1 vai 2 līkumi, bet kvarta polinomam ir līdz 3 līkumiem.

Pievienojot polinoma tendenču līniju Excel diagrammā, pakāpi norādiet, ierakstot atbilstošo skaitli laukā Pasūtījums lodziņā Formāts Trendline panelī, kas pēc noklusējuma ir 2: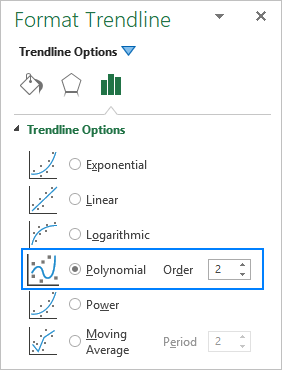

Piemēram, kvadrātiskā polinoma tendence ir redzama nākamajā grafikā, kurā parādīta saistība starp peļņu un to gadu skaitu, cik ilgi produkts ir bijis tirgū: pieaugums sākumā, maksimums vidū un kritums beigās.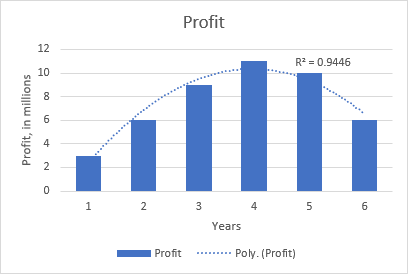

Jaudas tendences līnija

Jaudas tendences līnija ir ļoti līdzīga eksponenciālajai līknei, tikai tai ir simetriskāka līkne. To parasti izmanto, lai attēlotu mērījumus, kas pieaug ar noteiktu ātrumu.

Power Trendline nevar pievienot Excel diagrammai, kurā ir nulles vai negatīvas vērtības.

Kā piemēru, lai vizualizētu ķīmiskās reakcijas ātrumu, uzzīmēsim spēka tendenču līniju. Ievērojiet R kvadrāta vērtību 0,9918, kas nozīmē, ka mūsu tendenču līnija gandrīz pilnīgi atbilst datiem.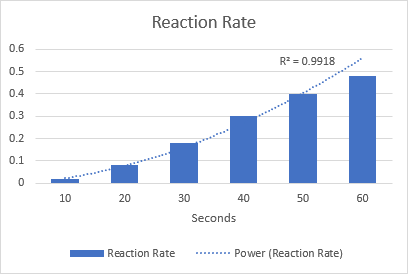

Kustīgā vidējā līnija

Ja diagrammas datu punktiem ir daudz kāpumu un kritumu, slīdošā vidējā tendences līnija var izlīdzināt datu vērtību galējās svārstības, lai skaidrāk parādītu modeli. Šim nolūkam Excel aprēķina slīdošo vidējo vērtību no norādītā periodu skaita (pēc noklusējuma 2) un iezīmē šīs vidējās vērtības kā punktus līnijā. Periods vērtība, jo vienmērīgāka līnija.

Labs praktisks piemērs ir slīdošās vidējās tendences līnijas izmantošana, lai atklātu akciju cenas svārstības, kuras citādi būtu grūti pamanīt.

Lai uzzinātu vairāk, skatiet: Kā Excel diagrammai pievienot slīdošo vidējo tendenču līniju.

Excel tendenču līnijas vienādojumi un formulas

Šajā sadaļā ir aprakstīti vienādojumi, ko Excel izmanto dažādiem tendenču līniju tipiem. Šīs formulas nav jāveido manuāli, vienkārši pasakiet Excel, lai diagrammā tiek parādīts tendenču līnijas vienādojums.

Mēs arī apspriedīsim formulu, lai atrastu tendenču līnijas slīpumu un citus koeficientus. Formulas pieņem, ka jums ir 2 mainīgo kopas: neatkarīgais mainīgais x un atkarīgais mainīgais y . Darblapās varat izmantot šīs formulas, lai iegūtu paredzamo vērtību. y vērtības jebkurai noteiktai vērtībai x .

Konsekvences labad visos piemēros izmantosim vienu un to pašu datu kopu ar nedaudz atšķirīgām vērtībām. Tomēr paturiet prātā, ka tas ir tikai demonstrācijas nolūkos. Reālajās darblapās jums jāizvēlas datu tipam atbilstošs tendenču līnijas tips.

Svarīga piezīme! Tendences līnijas formulas drīkst izmantot tikai ar XY izkliedes diagrammas jo tikai šajā diagrammā ir attēloti abi x un y asis kā skaitliskās vērtības. Lai iegūtu vairāk informācijas, skatiet tēmu Kāpēc Excel tendenču līnijas vienādojums var būt nepareizs.

Lineārās tendences vienādojums un formulas

Lineārās tendences vienādojums izmanto mazāko kvadrātu metodes, lai meklētu. slīpums un pārtvert koeficienti ir tādi, ka:

Kur:

• b ir slīpums tendences līnijas.
• a ir y-intercepcija , kas ir sagaidāmā vidējā vērtība y kad visi x mainīgie ir vienādi ar 0. Diagrammā tas ir punkts, kur līnija šķērso līniju. y ass.

Lineārajai regresijai programmā Microsoft Excel ir pieejamas īpašas funkcijas, lai iegūtu slīpuma un pārtveršanas koeficientus.

Tendences līnijas slīpums

b: =SLOPE(y,x)

Y-intercepcija

a: =INTERCEPT(y,x)

Pieņemot, ka x diapazons ir B2:B13 un y diapazons ir C2:C13, reālās formulas ir šādas:

= SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Tādus pašus rezultātus var iegūt, izmantojot LINEST funkciju kā masīva formula Šim nolūkam atlasiet 2 blakus esošas šūnas vienā rindā, ievadiet formulu un nospiediet Ctrl + Shift + Enter, lai to pabeigtu:

=LINEST(C2:C13,B2:B13)

Kā redzams zemāk redzamajā ekrānšāviņas attēlā, formulas atgrieztie slīpuma un pārtveršanas koeficienti pilnībā atbilst diagrammā attēlotā lineārās līknes vienādojuma koeficientiem, tikai pēdējie ir noapaļoti līdz 4 zīmēm aiz komata: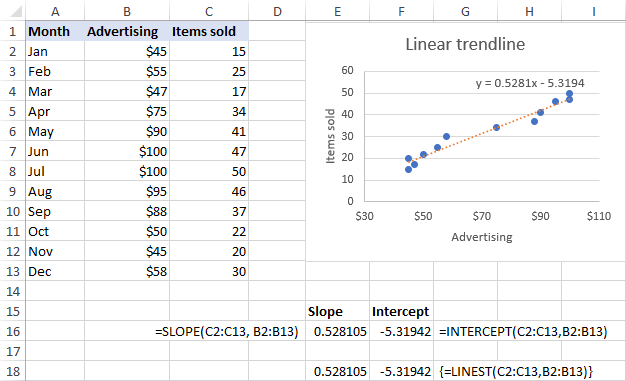

Eksponenciālās tendences vienādojums un formulas

Eksponenciālajai tendenču līnijai Excel izmanto šādu vienādojumu:

Kur a un b ir aprēķinātie koeficienti, un e ir matemātiskā konstante e (naturālā logaritma bāze).

Koeficientus var aprēķināt, izmantojot šīs vispārīgās formulas:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Mūsu parauga datu kopai formulas ir šādas:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logaritmiskās tendences līnijas vienādojums un formulas

Šeit ir logaritmiskās tendences līnijas vienādojums programmā Excel:

Kur a un b ir konstantes un ln ir naturālā logaritma funkcija.

Lai iegūtu konstantes, izmantojiet šīs vispārīgās formulas, kas atšķiras tikai ar pēdējo argumentu:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Mūsu izlases datu kopai mēs izmantojam šos datus:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polinoma tendences līnijas vienādojums un formulas

Lai aprēķinātu polinomu tendences līniju, Excel izmanto šo vienādojumu:

Kur b ₁ ... b ₆ un a ir konstantes.

Atkarībā no jūsu polinoma tendences līnijas pakāpes, konstantu iegūšanai izmantojiet vienu no šādām formulu kopām.

Kvadrātiskā (2. kārtas) polinoma tendences līnija

Vienādojums: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kubiskā (3. kārtas) polinoma tendenču līnija

Vienādojums: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Formulas augstākas pakāpes polinomu tendenču līnijām var izveidot, izmantojot to pašu modeli.

Mūsu datu kopai 2. kārtas polinoma tendences līnija ir piemērotāka, tāpēc mēs izmantojam šīs formulas:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)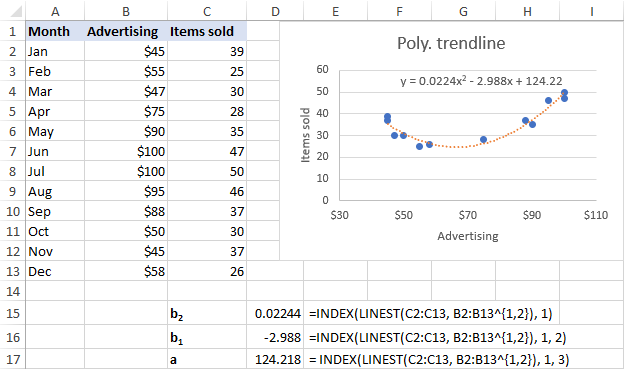

Jaudas tendenču vienādojums un formulas

Pamatojoties uz šo vienkāršo vienādojumu, programmā Excel tiek izveidota jaudas tendences līnija:

Kur a un b ir konstantes, kuras var aprēķināt pēc šīm formulām:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2)))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

Mūsu gadījumā lieliski darbojas šādas formulas:

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2)))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Excel tendenču līnijas vienādojums ir nepareizs - iemesli un labojumi

Ja domājat, ka Excel ir nepareizi uzzīmējis tendences līniju vai diagrammā redzamā tendences līnijas formula ir nepareiza, situāciju var izskaidrot šādi divi punkti.

Excel tendenču līnijas vienādojums ir pareizs tikai izkliedes diagrammās

Excel tendenču līnijas formulas jāizmanto tikai XY (izkliedes) diagrammām, jo tikai šajā diagrammas tipā gan y, gan x ass tiek attēlotas kā skaitliskas vērtības.

Lineārajās diagrammās, stabiņu un joslu diagrammās skaitliskās vērtības tiek attēlotas tikai uz y ass. x asi attēlo lineāra rinda (1, 2, 3,...) neatkarīgi no tā, vai ass marķējums ir skaitļi vai teksts. Kad šajās diagrammās izveidojat tendenču līniju, Excel izmanto šīs pieņemtās x vērtības tendenču līnijas formulā.

Skaitļi ir noapaļoti Excel tendenču līnijas vienādojumā

Lai aizņemtu mazāk vietas diagrammā, Excel parāda ļoti maz nozīmīgu ciparu tendenču līnijas vienādojumā. Jauki no dizaina viedokļa, taču tas ievērojami samazina formulas precizitāti, ja vienādojumā manuāli norādāt x vērtības.

Vienkāršs risinājums ir vienādojumā parādīt vairāk zīmju aiz komata aiz komata. Varat arī aprēķināt koeficientus, izmantojot formulu, kas atbilst jūsu tendenču līnijas tipam, un formatēt formulas šūnas tā, lai tajās būtu norādīts pietiekams zīmju aiz komata skaits aiz komata. Lai to izdarītu, vienkārši noklikšķiniet uz ikonas Palielināt decimāldaļu pogu uz Sākums cilnē Numurs grupa.

Tas ir veids, kā jūs varat izveidot dažādus tendenču līniju veidus programmā Excel un iegūt to vienādojumus. Paldies, ka izlasījāt, un ceru, ka nākamnedēļ tiksimies mūsu blogā!