In diesem Tutorial finden Sie eine ausführliche Beschreibung aller in Excel verfügbaren Trendlinien-Optionen und erfahren, wie Sie eine Trendlinien-Gleichung in einem Diagramm darstellen und die Steigung der Trendlinie ermitteln können.

Es ist sehr einfach, eine Trendlinie in Excel einzufügen. Die einzige wirkliche Herausforderung besteht darin, den Trendlinientyp zu wählen, der am besten zu den von Ihnen analysierten Daten passt. In diesem Tutorial finden Sie eine detaillierte Beschreibung aller Trendlinienoptionen, die in Excel zur Verfügung stehen, und wann sie zu verwenden sind. Wenn Sie wissen möchten, wie man eine Trendlinie in ein Excel-Diagramm einfügt, sehen Sie sich bitte das oben verlinkte Tutorial an.

Excel-Trendlinientypen

Beim Hinzufügen einer Trendlinie in Excel stehen Ihnen 6 verschiedene Optionen zur Verfügung. Außerdem ermöglicht Microsoft Excel die Anzeige einer Trendliniengleichung und eines R-Quadratwerts in einem Diagramm:

• Trendlinien-Gleichung ist eine Formel, die eine Linie findet, die am besten zu den Datenpunkten passt.
• R-Quadrat-Wert misst die Zuverlässigkeit der Trendlinie - je näher R2 bei 1 liegt, desto besser passt die Trendlinie zu den Daten.

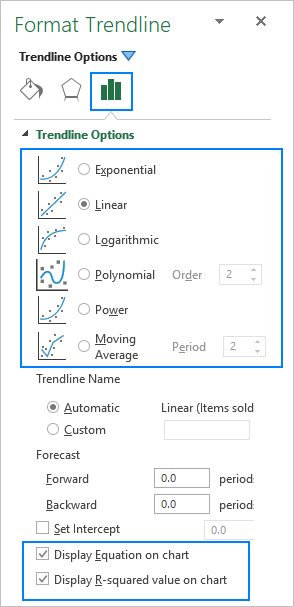
Nachfolgend finden Sie eine kurze Beschreibung der einzelnen Trendlinientypen mit Diagrammbeispielen.

Lineare Trendlinie

Die lineare Trendlinie wird am besten bei linearen Datensätzen verwendet, wenn die Datenpunkte in einem Diagramm einer geraden Linie ähneln. Normalerweise beschreibt eine lineare Trendlinie einen kontinuierlichen Anstieg oder Abfall im Laufe der Zeit.

Die folgende lineare Trendlinie zeigt beispielsweise einen stetigen Anstieg der Verkäufe über einen Zeitraum von sechs Monaten, und der R2-Wert von 0,9855 deutet darauf hin, dass die geschätzten Werte der Trendlinie recht gut mit den tatsächlichen Daten übereinstimmen.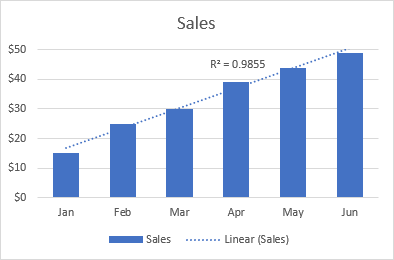

Exponentiale Trendlinie

Die exponentielle Trendlinie ist eine gekrümmte Linie, die einen Anstieg oder Rückgang der Datenwerte mit zunehmender Geschwindigkeit veranschaulicht; daher ist die Linie in der Regel an einer Seite stärker gekrümmt. Dieser Trendlinientyp wird häufig in der Wissenschaft verwendet, um beispielsweise das Wachstum der menschlichen Bevölkerung oder den Rückgang von Wildtierpopulationen zu veranschaulichen.

Bitte beachten Sie, dass eine exponentielle Trendlinie nicht für Daten erstellt werden kann, die Nullen oder negative Werte enthalten.

Ein gutes Beispiel für eine Exponentialkurve ist der Rückgang der gesamten Wildtigerpopulation auf der Erde.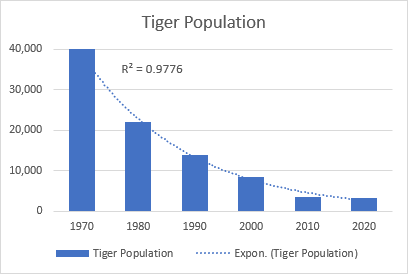

Logarithmische Trendlinie

Die logarithmische Best-Fit-Linie wird im Allgemeinen verwendet, um Daten darzustellen, die schnell ansteigen oder abfallen und dann abflachen. Sie kann sowohl positive als auch negative Werte enthalten.

Ein Beispiel für eine logarithmische Trendlinie ist die Inflationsrate, die zunächst ansteigt, sich aber nach einer Weile stabilisiert.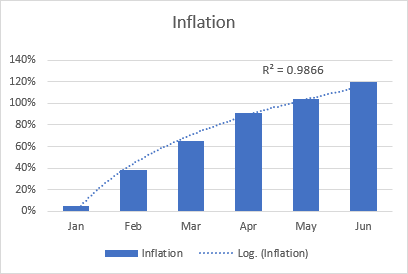

Polynomielle Trendlinie

Die polynomial gekrümmte Trendlinie eignet sich gut für große Datensätze mit oszillierenden Werten, die mehr als einen Anstieg und Abfall aufweisen.

Im Allgemeinen wird ein Polynom nach dem Grad des größten Exponenten klassifiziert. Der Grad der Polynomtrendlinie kann auch durch die Anzahl der Biegungen in einem Diagramm bestimmt werden. Typischerweise hat eine quadratische Polynomtrendlinie eine Biegung (Berg oder Tal), ein kubisches Polynom hat 1 oder 2 Biegungen und ein quartisches Polynom hat bis zu 3 Biegungen.

Wenn Sie eine polynomiale Trendlinie in ein Excel-Diagramm einfügen, geben Sie den Grad an, indem Sie die entsprechende Zahl in das Feld Bestellung Feld auf der Format Trendlinie der standardmäßig auf 2 eingestellt ist: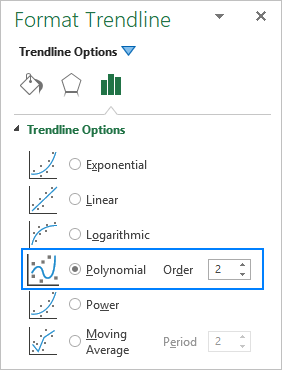

Der quadratische Polynomtrend ist beispielsweise in der folgenden Grafik zu erkennen, die die Beziehung zwischen dem Gewinn und der Anzahl der Jahre, die das Produkt auf dem Markt ist, zeigt: Anstieg zu Beginn, Spitzenwert in der Mitte und Rückgang gegen Ende.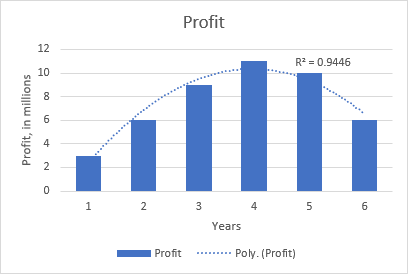

Trendlinie Leistung

Die Leistungstrendlinie ist der Exponentialkurve sehr ähnlich, nur dass sie einen symmetrischeren Bogen hat. Sie wird häufig verwendet, um Messungen darzustellen, die mit einer bestimmten Rate ansteigen.

Eine Power-Trendlinie kann nicht zu einem Excel-Diagramm hinzugefügt werden, das Null- oder negative Werte enthält.

Zeichnen wir als Beispiel eine Potenz-Trendlinie, um die chemische Reaktionsgeschwindigkeit zu visualisieren. Beachten Sie den R-Quadrat-Wert von 0,9918, was bedeutet, dass unsere Trendlinie fast perfekt zu den Daten passt.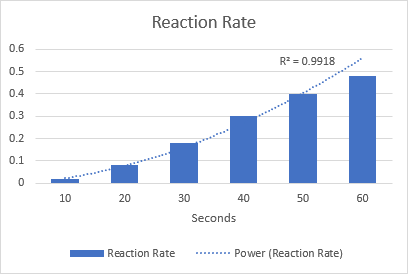

Trendlinie des gleitenden Durchschnitts

Wenn die Datenpunkte in Ihrem Diagramm viele Höhen und Tiefen aufweisen, kann eine Trendlinie mit gleitendem Durchschnitt die extremen Schwankungen der Datenwerte glätten, um ein Muster deutlicher zu zeigen. Dazu berechnet Excel den gleitenden Durchschnitt der von Ihnen angegebenen Anzahl von Perioden (standardmäßig 2) und setzt diese Durchschnittswerte als Punkte in die Linie. Je höher der Zeitraum Wert, desto glatter ist die Linie.

Ein gutes praktisches Beispiel ist die Verwendung der Trendlinie des gleitenden Durchschnitts, um Schwankungen eines Aktienkurses aufzudecken, die sonst nur schwer zu beobachten wären.

Weitere Informationen finden Sie unter: Hinzufügen einer gleitenden Durchschnittstrendlinie zu einem Excel-Diagramm.

Excel-Trendliniengleichungen und -formeln

In diesem Abschnitt werden die Gleichungen beschrieben, die Excel für die verschiedenen Trendlinientypen verwendet. Sie müssen diese Formeln nicht manuell erstellen, sondern können Excel einfach anweisen, die Trendliniengleichung in einem Diagramm anzuzeigen.

Außerdem werden wir die Formel zur Ermittlung der Steigung einer Trendlinie und anderer Koeffizienten besprechen. Die Formeln gehen davon aus, dass Sie 2 Sätze von Variablen haben: unabhängige Variable x und abhängige Variable y In Ihren Arbeitsblättern können Sie diese Formeln verwenden, um die vorhergesagten Werte zu erhalten. y Werte für alle gegebenen Werte von x .

Aus Gründen der Konsistenz werden wir für alle Beispiele denselben Datensatz mit leicht variierenden Werten verwenden. Beachten Sie jedoch, dass dies nur zu Demonstrationszwecken dient. In Ihren echten Arbeitsblättern sollten Sie den Trendlinientyp wählen, der Ihrem Datentyp entspricht.

Wichtiger Hinweis: Die Trendlinienformeln sollten nur mit XY-Punktdiagramme denn nur dieses Diagramm zeigt beide x und y Weitere Informationen finden Sie unter Warum die Excel-Trendliniengleichung falsch sein kann.

Lineare Trendliniengleichung und Formeln

Die lineare Trendliniengleichung verwendet die Methode der kleinsten Quadrate, um die Piste und abfangen. Koeffizienten, so dass:

Wo:

• b ist die Piste einer Trendlinie.
• a ist die y-Achsenabschnitt das ist der erwartete Mittelwert von y wenn alle x Variablen gleich 0 sind. In einem Diagramm ist dies der Punkt, an dem sich die Trendlinie mit der y Achse.

Für die lineare Regression bietet Microsoft Excel spezielle Funktionen zur Ermittlung der Steigungs- und Achsenabschnittskoeffizienten.

Steigung der Trendlinie

b: =SLOPE(y,x)

Y-Achsenabschnitt

a: =INTERCEPT(y,x)

Unter der Annahme, dass die x Bereich ist B2:B13 und der y Bereich C2:C13 ist, lauten die Formeln in der Praxis wie folgt:

=STEILHEIT(C2:C13, B2:B13)

=ABSCHNITT(C2:C13,B2:B13)

Die gleichen Ergebnisse lassen sich durch die Verwendung der Funktion LINEST als Matrixformel Markieren Sie dazu 2 benachbarte Zellen in derselben Zeile, geben Sie die Formel ein und drücken Sie Strg + Umschalt + Enter, um sie abzuschließen:

=LINEST(C2:C13,B2:B13)

Wie in der nachstehenden Abbildung zu sehen ist, stimmen die von den Formeln zurückgegebenen Steigungs- und Achsenabschnittskoeffizienten genau mit den Koeffizienten der im Diagramm angezeigten linearen Trendliniengleichung überein, nur dass letztere auf 4 Dezimalstellen gerundet sind: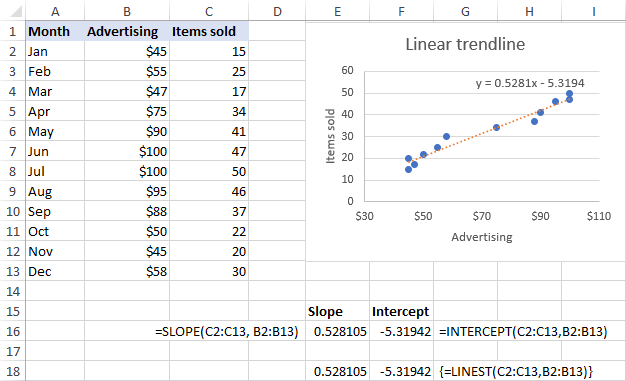

Exponentiale Trendliniengleichung und Formeln

Für die exponentielle Trendlinie verwendet Excel die folgende Gleichung:

Wo a und b sind berechnete Koeffizienten und e ist die mathematische Konstante e (die Basis des natürlichen Logarithmus).

Die Koeffizienten können mit Hilfe dieser allgemeinen Formeln berechnet werden:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Für unseren Beispieldatensatz sehen die Formeln wie folgt aus:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logarithmische Trendliniengleichung und Formeln

Hier ist die logarithmische Trendliniengleichung in Excel:

Wo a und b sind Konstanten und ln ist die Funktion des natürlichen Logarithmus.

Um die Konstanten zu erhalten, verwenden Sie diese allgemeinen Formeln, die sich nur durch das letzte Argument unterscheiden:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Für unseren Beispieldatensatz verwenden wir diese:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polynomiale Trendliniengleichung und Formeln

Um die polynomiale Trendlinie zu berechnen, verwendet Excel diese Gleichung:

Wo b ₁ ... b ₆ und a sind Konstanten.

Verwenden Sie je nach Grad der polynomialen Trendlinie eine der folgenden Formeln, um die Konstanten zu ermitteln.

Quadratische (2. Ordnung) polynomische Trendlinie

Gleichung: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kubische (3. Ordnung) polynomiale Trendlinie

Gleichung: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Die Formeln für polynomiale Trendlinien höheren Grades können nach demselben Muster erstellt werden.

Für unseren Datensatz eignet sich die polynomiale Trendlinie 2. Ordnung besser, weshalb wir diese Formeln verwenden:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)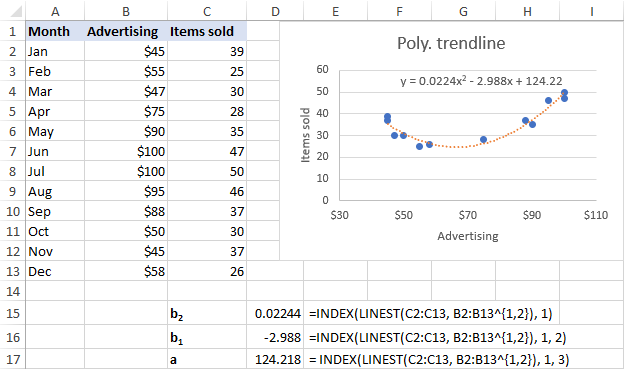

Leistungs-Trendlinien-Gleichung und Formeln

Eine Power-Trendlinie in Excel wird auf der Grundlage dieser einfachen Gleichung gezeichnet:

Wo a und b sind Konstanten, die mit diesen Formeln berechnet werden können:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),), 1)

In unserem Fall haben sich die folgenden Formeln bewährt:

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),), 1)

Excel-Trendliniengleichung ist falsch - Gründe und Korrekturen

Wenn Sie der Meinung sind, dass Excel eine Trendlinie falsch gezeichnet hat oder die in Ihrem Diagramm angezeigte Trendlinienformel falsch ist, können die folgenden zwei Punkte etwas Licht in die Situation bringen.

Die Excel-Trendliniengleichung ist nur in Streudiagrammen korrekt

Excel-Trendlinienformeln sollten nur bei XY-Diagrammen (Punktdiagrammen) verwendet werden, da nur bei diesem Diagrammtyp sowohl die y-Achse als auch die x-Achse als numerische Werte aufgetragen werden.

In Linien-, Säulen- und Balkendiagrammen werden numerische Werte nur auf der y-Achse aufgetragen. Die x-Achse wird durch eine lineare Reihe (1, 2, 3,...) dargestellt, unabhängig davon, ob die Achsenbeschriftungen Zahlen oder Text sind. Wenn Sie in diesen Diagrammen eine Trendlinie erstellen, verwendet Excel diese angenommenen x-Werte in der Trendlinienformel.

In der Excel-Trendliniengleichung werden die Zahlen gerundet.

Um weniger Platz im Diagramm zu beanspruchen, zeigt Excel nur wenige signifikante Stellen in einer Trendliniengleichung an. Das ist zwar schön, verringert aber die Genauigkeit der Formel erheblich, wenn Sie die x-Werte manuell in die Gleichung eingeben.

Eine einfache Lösung besteht darin, mehr Nachkommastellen in der Gleichung anzuzeigen. Alternativ können Sie die Koeffizienten berechnen, indem Sie eine Formel verwenden, die Ihrem Trendlinientyp entspricht, und die Formelzellen so formatieren, dass sie eine ausreichende Anzahl von Nachkommastellen aufweisen. Klicken Sie dazu einfach auf die Schaltfläche Dezimalwert erhöhen auf der Schaltfläche Startseite auf der Registerkarte Nummer Gruppe.

So können Sie verschiedene Trendlinientypen in Excel erstellen und deren Gleichungen erhalten. Ich danke Ihnen für die Lektüre und hoffe, Sie nächste Woche in unserem Blog begrüßen zu dürfen!