I den här handledningen hittar du en detaljerad beskrivning av alla trendlinjealternativ som finns i Excel och när du ska använda dem. Du lär dig också hur du visar en trendlinjekvation i ett diagram och hur du hittar trendlinjens lutning.

Det är mycket enkelt att lägga till en trendlinje i Excel. Den enda verkliga utmaningen är att välja den trendlinjetyp som bäst motsvarar den typ av data som du analyserar. I den här handledningen hittar du en detaljerad beskrivning av alla de trendlinjealternativ som finns i Excel och när du ska använda dem. Om du letar efter hur du infogar en trendlinje i ett Excel-diagram, vänligen kolla in den ovan länkade handledningen.

Excel trendlinjetyper

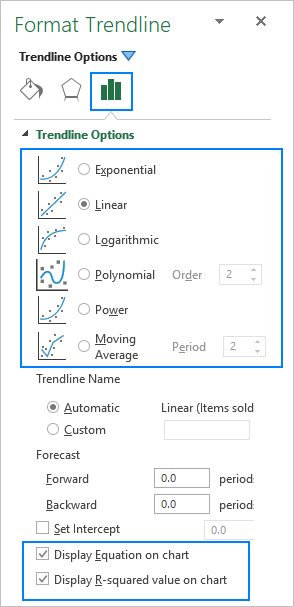
När du lägger till en trendlinje i Excel har du sex olika alternativ att välja mellan. Microsoft Excel gör det dessutom möjligt att visa trendlinjens ekvation och R-kvadratvärde i ett diagram:

• Ekvation för trendlinje är en formel som hittar en linje som passar bäst till datapunkterna.
• R-kvadratvärde mäter trendlinjens tillförlitlighet - ju närmare R2 är 1, desto bättre passar trendlinjen in på data.

Nedan hittar du en kort beskrivning av varje trendlinjetyp med exempel på diagram.

Linjär trendlinje

Den linjära trendlinjen används bäst för linjära datamängder när datapunkterna i diagrammet liknar en rak linje. Typiskt sett beskriver en linjär trendlinje en kontinuerlig ökning eller minskning över tiden.

Följande linjära trendlinje visar till exempel en stadig ökning av försäljningen under sex månader, och R2-värdet på 0,9855 visar att de uppskattade trendlinjevärdena stämmer ganska bra överens med de faktiska uppgifterna.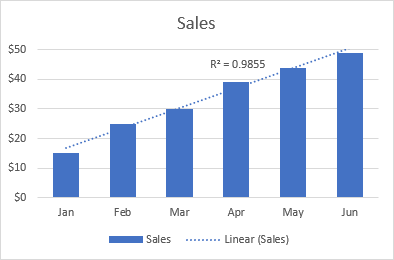

Exponentiell trendlinje

Den exponentiella trendlinjen är en böjd linje som illustrerar en ökning eller minskning av datavärden i ökande takt, därför är linjen vanligtvis mer böjd på ena sidan. Denna trendlinjetyp används ofta inom vetenskapen, till exempel för att visualisera en befolkningstillväxt eller en minskning av vilda djurpopulationer.

Observera att en exponentiell trendlinje inte kan skapas för data som innehåller nollor eller negativa värden.

Ett bra exempel på en exponentiell kurva är minskningen av hela den vilda tigerpopulationen på jorden.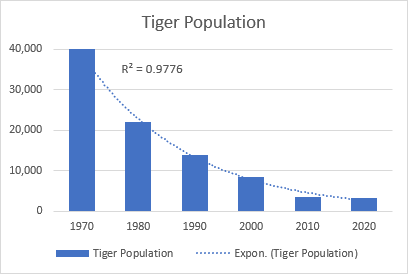

Logaritmisk trendlinje

Den logaritmiska linjen med bästa anpassning används i allmänhet för att plotta data som snabbt ökar eller minskar för att sedan plana ut. Den kan innehålla både positiva och negativa värden.

Ett exempel på en logaritmisk trendlinje kan vara inflationen, som först ökar men som efter ett tag stabiliseras.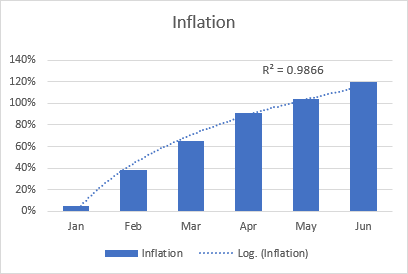

Polynomisk trendlinje

Den polynomiala kurvilinjära trendlinjen fungerar bra för stora datamängder med oscillerande värden som har mer än en uppgång och nedgång.

Generellt sett klassificeras ett polynom genom graden av den största exponenten. Graden av polynomtrendlinjen kan också bestämmas genom antalet krökar i grafen. Typiskt sett har en kvadratisk polynomtrendlinje en krök (backe eller dal), ett kubiskt polynom har en eller två krökar och ett kvartiskt polynom har upp till tre krökar.

När du lägger till en polynomial trendlinje i ett Excel-diagram anger du graden genom att skriva motsvarande siffra i fältet Beställ på den Format Trendline som är 2 som standard: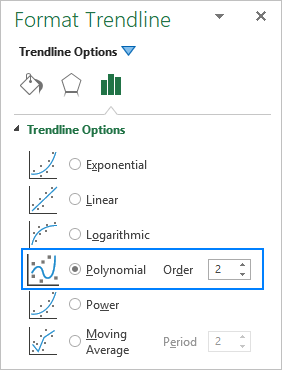

Den kvadratiska polynomiala trenden är till exempel tydlig i följande diagram som visar förhållandet mellan vinsten och antalet år som produkten har funnits på marknaden: ökning i början, topp i mitten och minskning mot slutet.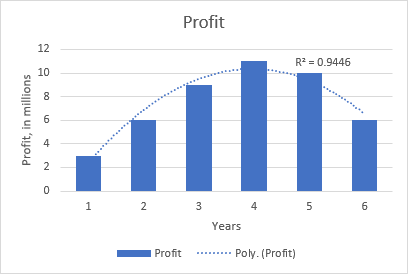

Power trendline

Effekttrendlinjen är mycket lik exponentialkurvan, men den har en mer symmetrisk båge. Den används ofta för att plotta mätningar som ökar i en viss takt.

En Power Trendline kan inte läggas till i ett Excel-diagram som innehåller noll eller negativa värden.

Som exempel kan vi rita en trendlinje för att visualisera den kemiska reaktionshastigheten. Observera R-kvadratvärdet på 0,9918, vilket innebär att vår trendlinje passar nästan perfekt till data.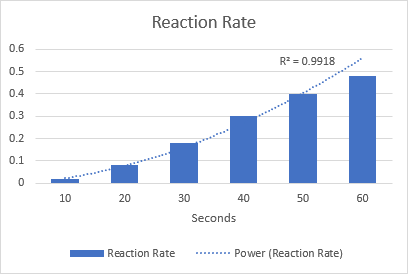

Rörligt medelvärde trendlinje

När datapunkterna i diagrammet har många upp- och nedgångar kan en trendlinje med glidande medelvärde jämna ut de extrema fluktuationerna i datavärdena för att visa ett mönster tydligare. Excel beräknar det glidande medelvärdet för det antal perioder som du anger (2 som standard) och placerar dessa medelvärden som punkter på linjen. Period värdet, desto jämnare blir linjen.

Ett bra praktiskt exempel är att använda trendlinjen för glidande medelvärde för att avslöja fluktuationer i aktiekursen som annars skulle vara svåra att observera.

För mer information, se: Hur man lägger till en trendlinje för glidande medelvärde i ett Excel-diagram.

Excel trendline ekvationer och formler

I det här avsnittet beskrivs de ekvationer som Excel använder för olika trendlinjetyper. Du behöver inte skapa dessa formler manuellt, utan du behöver bara be Excel att visa trendlinjeekvationen i ett diagram.

Vi kommer också att diskutera formeln för att hitta lutningen på en trendlinje och andra koefficienter. Formlerna förutsätter att du har två uppsättningar variabler: oberoende variabel x och beroende variabel y I dina kalkylblad kan du använda dessa formler för att få fram de beräknade y värden för alla givna värden för x .

För konsekvensens skull kommer vi att använda samma datamängd med något varierande värden i alla exemplen. Tänk dock på att det bara är i demonstrationssyfte. I dina riktiga arbetsblad ska du välja den trendlinjetyp som motsvarar din datatyp.

Viktigt att notera: Formlerna för trendlinjer bör endast användas med XY-spridningsdiagram eftersom endast detta diagram visar båda x och y axlar som numeriska värden. För mer information, se Varför Excel trendlinjeekvation kan vara fel.

Ekvation och formler för linjär trendlinje

Den linjära trendlinjekvationen använder minsta kvadratmetoden för att söka efter den lutning och intercept koefficienter så att:

Var:

• b är den lutning av en trendlinje.
• a är den y-intercept , som är det förväntade medelvärdet av y när alla x variabler är lika med 0. På ett diagram är det den punkt där trendlinjen korsar y axel.

För linjär regression tillhandahåller Microsoft Excel särskilda funktioner för att få fram koefficienterna för lutning och intercept.

Trendlinjens lutning

b: =SLOPE(y,x)

Y-intercept

a: =INTERCEPT(y,x)

Om man utgår från att x är B2:B13 och y är C2:C13, och de verkliga formlerna är följande:

=LOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Samma resultat kan uppnås genom att använda LINEST-funktionen som en formel för matris För detta markerar du två intilliggande celler i samma rad, skriver in formeln och trycker på Ctrl + Shift + Enter för att slutföra den:

=LINEST(C2:C13,B2:B13)

Som framgår av skärmdumpen nedan är de koefficienter för lutning och intercept som formlerna ger upphov till helt i linje med koefficienterna i ekvationen för den linjära trendlinjen som visas i diagrammet, men de sistnämnda är avrundade till fyra decimaler: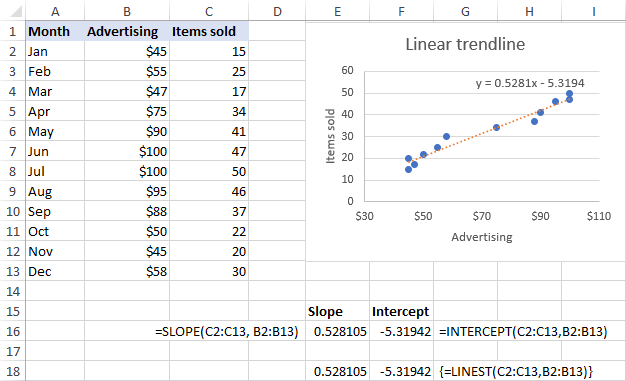

Ekvation och formler för exponentiell trendlinje

För den exponentiella trendlinjen använder Excel följande ekvation:

Var a och b är beräknade koefficienter och e är den matematiska konstanten e (basen för den naturliga logaritmen).

Koefficienterna kan beräknas med hjälp av dessa generiska formler:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

För vårt datamaterial har formlerna följande utformning:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logaritmisk trendlinje ekvation och formler

Här är ekvationen för logaritmisk trendlinje i Excel:

Var a och b är konstanter och ln är den naturliga logaritmens funktion.

För att få fram konstanterna använder du dessa generiska formler, som endast skiljer sig åt i det sista argumentet:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

För vårt datamaterial använder vi dessa:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polynomial trendlinje ekvation och formler

Excel använder den här ekvationen för att räkna ut den polynomiska trendlinjen:

Var b ₁ ... b ₆ och a är konstanter.

Beroende på graden av din polynomiala trendlinje kan du använda någon av följande formler för att få fram konstanterna.

Kvadratisk (2:a ordningen) polynomisk trendlinje

Ekvation: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kubisk (3:e ordningen) polynomisk trendlinje

Ekvation: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Formlerna för polynomiala trendlinjer av högre grad kan byggas upp enligt samma mönster.

För vårt dataset passar den polynomiska trendlinjen av andra ordningen bättre, så vi använder dessa formler:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)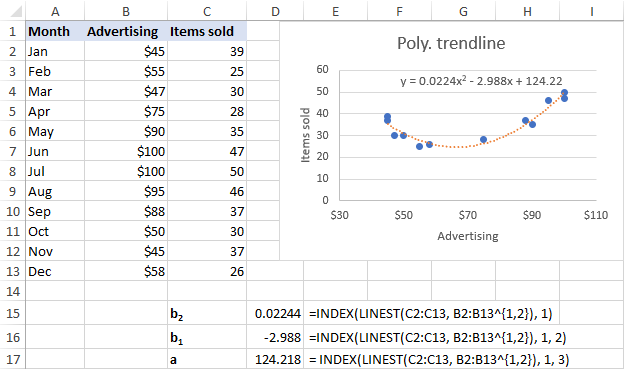

Power trendline ekvation och formler

En Power Trendline i Excel ritas utifrån denna enkla ekvation:

Var a och b är konstanter som kan beräknas med dessa formler:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

I vårt fall fungerar följande formler utmärkt:

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2)))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Excel trendlinjeekvation är fel - orsaker och lösningar

Om du tror att Excel har ritat en trendlinje felaktigt eller att formeln för trendlinjen som visas i diagrammet är felaktig, kan följande två punkter kasta lite ljus över situationen.

Excel trendlinjeekvation är korrekt endast i spridningsdiagram.

Excel-formler för trendlinjer bör endast användas med XY-grafer (spridningsdiagram) eftersom både y-axeln och x-axeln endast i den här diagramtypen plottas som numeriska värden.

I linjediagram, kolumn- och stapeldiagram visas numeriska värden endast på y-axeln. X-axeln representeras av en linjär serie (1, 2, 3,...) oavsett om axelbeteckningarna är siffror eller text. När du skapar en trendlinje i dessa diagram använder Excel de antagna x-värdena i trendlinjeformeln.

Siffrorna är avrundade i Excel-ekvationen för trendlinje.

För att ta mindre plats i diagrammet visar Excel väldigt få signifikanta siffror i en trendlineekvation. Det är snyggt designmässigt, men det minskar formelns noggrannhet avsevärt när du manuellt anger x-värden i ekvationen.

En enkel lösning är att visa fler decimaler i ekvationen. Alternativt kan du beräkna koefficienterna genom att använda en formel som motsvarar din trendlinjetyp och formatera formelcellerna så att de visar tillräckligt många decimaler. För detta klickar du helt enkelt på Öka decimaltalet på knappen på Hem på fliken Antal grupp.

Så kan du skapa olika typer av trendlinjer i Excel och få fram deras ekvationer. Tack för att du läste och hoppas att vi ses på vår blogg nästa vecka!