Tutorial honetan, Excel-en eskuragarri dauden joera-aukera guztien deskribapen zehatza aurkituko duzu eta noiz erabili. Joera-lerroaren ekuazioa grafiko batean nola bistaratzen eta joera-lerroaren malda aurkitzen ere ikasiko duzu.

Oso erraza da Excel-en joera-lerroa gehitzea. Benetako erronka bakarra aztertzen ari zaren datu motarekin hobekien egokitzen den joera-lerroa aukeratzea da. Tutorial honetan, Excel-en eskuragarri dauden joera-aukera guztien deskribapen zehatza aurkituko duzu eta noiz erabili. Excel-eko grafiko batean joera-lerroa nola txertatu bilatzen ari bazara, begiratu goiko estekatutako tutoriala.

Excel joera-lerro motak

Excel-en joera-lerroa gehitzean. , 6 aukera ezberdin dituzu aukeran. Gainera, Microsoft Excel-ek joera-lerroaren ekuazioa eta R karratuaren balioa grafiko batean bistaratzeko aukera ematen du:

• Joera-lerroaren ekuazioa datu-puntuetara hobekien egokitzen den lerroa aurkitzen duen formula da.
• R koadratuko balioak k joera-lerroaren fidagarritasuna neurtzen du; R2 zenbat eta gertuago egon 1etik, orduan eta hobeto egokitzen da joera-lerroa datuetara.

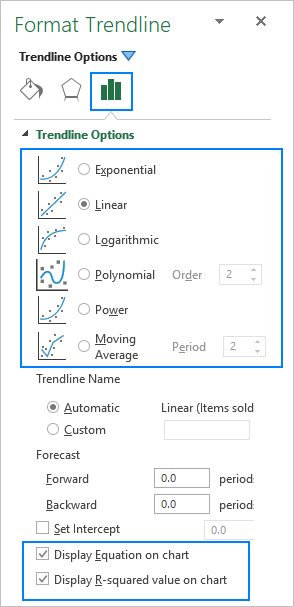
Behean, joera-lerro mota bakoitzaren deskribapen laburra aurkituko duzu grafikoen adibideekin.

Joera-lerro lineala

Joera-lerro lineala hobe da. datu-multzo linealekin erabiltzen da diagrama bateko datu-puntuak lerro zuzen baten antza dutenean. Normalean, joera lineal batek etengabeko igoera edo jaitsiera deskribatzen dudenboran zehar.

Adibidez, hurrengo joera lineal honek 6 hilabetetan zehar salmenten hazkunde etengabea erakusten du. Eta 0,9855-ren R2 balioak estimatutako joera-lerroaren balioak benetako datuekin nahiko ondo egokitzen direla adierazten du.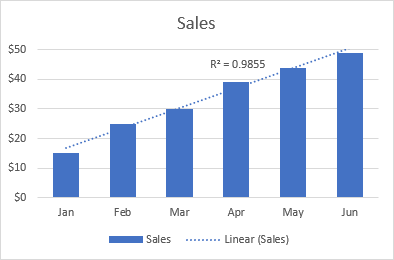

Joera-lerro esponentziala

Joera-lerro esponentziala datu-balioen gorakada edo beherakada gero eta abiadura handiagoan adierazten duen lerro kurbatua da; beraz, lerroa kurbatuagoa izan ohi da alde batean. Joera-lerro mota hau maiz erabiltzen da zientzietan, adibidez, giza populazioaren hazkundea edo fauna-populazioen beherakada ikusteko.

Kontuan izan ezin dela sortu joera-lerro esponentzial bat zeroak edo balio negatiboak dituzten datuetarako.

Kurba esponentzial baten adibide ona lurreko tigre basatien populazio osoaren desintegrazioa da.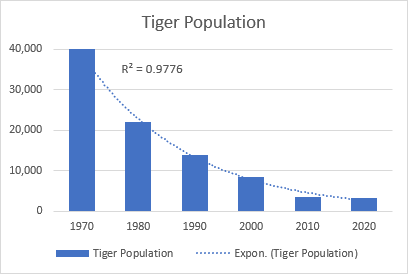

Joera-lerroa logaritmikoa

Egokipen onenaren lerro logaritmikoa, oro har, azkar handitzen edo txikitzen eta gero berdintzen diren datuak marrazteko erabiltzen da. Balio positiboak eta negatiboak izan ditzake.

Joera-lerro logaritmikoaren adibide bat inflazio-tasa izan daiteke, lehenik gora egiten ari dena baina pixka bat igaro ondoren egonkortzen dena.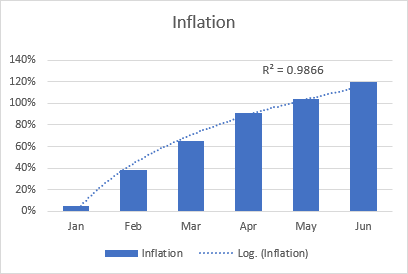

Joera-lerro polinomiala

Joera-lerro polinomial kurbilineoak ondo funtzionatzen du igoera eta beherakada bat baino gehiago dituzten balio oszilatzaileak dituzten datu multzo handietarako.

Oro har, polinomio bat arabera sailkatzen da. berretzaile handienaren gradua. Joera-lerro polinomialaren gradua izan daitekegrafiko baten bihurgune kopuruaren arabera ere zehaztuko da. Normalean, polinomio koadratikoko joera-lerroak bihurgune bat du (muinoa edo harana), polinomio kubiko batek 1 edo 2 bihurgune ditu eta polinomio kuartiko batek gehienez 3 bihurgune ditu.

Excel grafiko batean joera polinomiko bat gehitzean, gradua zehazten duzu Ordena koadroan dagokion zenbakia idatziz Formatu joera-lerroa panelean, hau da, lehenespenez 2: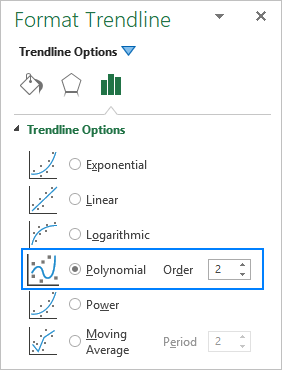

Adibidez, joera polinomiko koadratikoa. mozkinaren eta produktuak merkatuan daraman urte kopuruaren arteko erlazioa erakusten duen grafiko honetan nabaria da: hasieran igoera, erdialdean gailurra eta amaieratik gertu jaitsiera.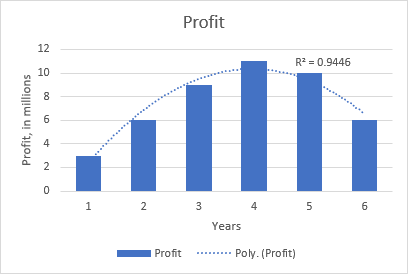

Potentzia-joera-lerroa

Potentzia-joera-lerroa kurba esponentzialaren oso antzekoa da, arku simetrikoagoa du soilik. Gehienetan erabiltzen da abiadura jakin batean hazten diren neurketak irudikatzeko.

Ezin da balio zero edo negatiboak dituen Excel grafiko batean potentzia-joera-lerroa gehitu.

Adibide gisa, marraz dezagun potentzia joera-lerroa erreakzio kimikoaren abiadura ikusteko. Kontuan izan 0,9918-ren R karratuaren balioa, eta horrek esan nahi du gure joera-lerroa datuetara ia ezin hobeto egokitzen dela.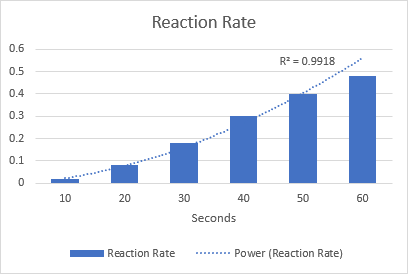

Batez besteko joera-lerroa

Zure grafikoko datu-puntuek gora-behera asko dituztenean, batez besteko joera-lerro mugikor batek datuen balioen muturreko gorabeherak leun ditzake eredu bat argiago erakusteko. Horretarako, Excel-ek kalkulatzen duZehazten duzun periodo kopuruaren batez besteko mugikorra (2 lehenespenez) eta batez besteko balio horiek lerroan puntu gisa jartzen ditu. Aldia balioa zenbat eta handiagoa izan, orduan eta leunagoa izango da lerroa.

Adibide praktiko on bat batez besteko joera-lerroa erabiltzea da, bestela behatzea zaila izango litzatekeen akzioen prezioaren gorabeherak agertzeko.

Informazio gehiago lortzeko, ikus: Nola gehitu batez besteko mugimenduko joera-lerroa Excel-eko taula batean.

Excel-en joera-lerroaren ekuazioak eta formulak

Atal honetan Excel-ek erabiltzen dituen ekuazioak deskribatzen dira. joera-lerro mota desberdinetarako. Ez dituzu formula hauek eskuz eraiki behar, besterik gabe, esan Excel-i joera-lerroaren ekuazioa grafiko batean bistaratzeko.

Gainera, joera-lerro baten malda eta beste koefiziente batzuk aurkitzeko formula ere eztabaidatuko dugu. Formulek 2 aldagai multzo dituzula suposatzen dute: x aldagai independentea eta y aldagai menpekoa . Zure lan-orrietan, formula hauek erabil ditzakezu aurreikusitako y balioak lortzeko x balio jakin batzuetarako.

Koherentzia izateko, datu berdinak erabiliko ditugu. adibide guztietarako balio apur bat aldakorrekin ezarri. Hala ere, gogoan izan erakustaldietarako soilik dela. Zure benetako lan-orrietan, zure datu-motari dagokion joera-lerroa aukeratu beharko zenuke.

Ohar garrantzitsua! Joera-lerroaren formulak XY sakabanatze diagramekin soilik erabili behar dira, hau bakarrik delakodiagramak x zein y ardatzak marrazten ditu zenbakizko balio gisa. Informazio gehiago lortzeko, ikusi Zergatik oker egon daitekeen Excel joera-lerroaren ekuazioa.

Joera-lerroaren ekuazio lineala eta formulak

Joera-lerroaren ekuazio linealak karratu txikienen metodoak erabiltzen ditu malda bilatzeko. eta ebakitzeko koefizienteak:

y = bx + a

Non:

• b malda den. Joera-lerro baten.
• a y-ebakidura da, hau da, y espero den batez besteko balioa x aldagaiak 0ren berdinak dira. Grafiko batean, joera-lerroak y ardatza zeharkatzen duen puntua da.

Erregresio linealerako, Microsoft Excel-ek funtzio bereziak eskaintzen ditu. malda eta ebakidura-koefizienteak.

Joera-lerroaren malda

b: =SLOPE(y,x)

Y-ebakidura

a: =INTERCEPT(y,x)

x barrutia B2:B13 dela eta y tartea C2:C13 dela suposatuz, bizitza errealeko formulak honela doaz:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Emaitza berdinak lor daitezke LINEST funtzioa array formula gisa erabiliz. Horretarako, hautatu ondoko 2 gelaxka errenkada berean, sartu formula eta sakatu Ctrl + Shift + Sartu osatzeko:

=LINEST(C2:C13,B2:B13)

Beheko pantaila-argazkian erakusten den moduan, malda eta interzepzioa. Formulek itzultzen dituzten koefizienteak guztiz bat datoz grafikoan agertzen den joera-lerroaren ekuazio linealeko koefizienteekin, azken hauek bakarrik 4 hamartarrekin biribiltzen dira: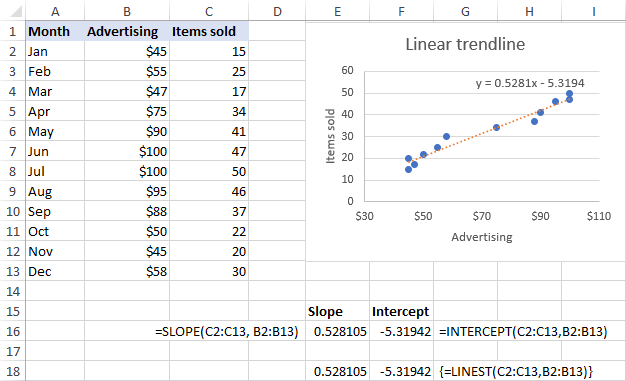

Joera-lerro esponentzialaren ekuazioa eta formulak

Joera-lerro esponentzialerako, Excel-ek honako ekuazio hau erabiltzen du:

y = aebx

Non a eta b kalkulatutako koefizienteak dira eta e e konstante matematikoa da (logaritmo naturalaren oinarria).

Koefizienteak formula generiko hauek erabiliz kalkula daitezke:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Gure lagin-datu multzorako, formulek forma hau hartzen dute:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Joera-lerroaren ekuazioa eta formula logaritmikoak

Hona hemen Excel-en joera-lerroaren ekuazioa logaritmikoa:

y = a*ln(x)+b

Non a eta b konstanteak dira eta ln logaritmo funtzio naturala da.

Konstanteak lortzeko, erabili formula generiko hauek, azken argumentuan soilik desberdinak direnak:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Gure lagin-datu multzorako, hauek erabiltzen ditugu:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Joera-lerro polinomikoen ekuazioa eta formulak

Joera-lerro polinomiala lantzeko, Excel-ek ekuazio hau erabiltzen du:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Non b ₁ … b ₆ eta a konstanteak dira.

Zure joera-lerro polinomialaren graduaren arabera, erabili formula-multzo hauetako bat. konstanteak lortzeko.

Joera-lerro polinomio koadratikoa (2. ordena)

Ekuazioa: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Joera-lerro polinomial kubikoa (3. ordena)

Ekuazioa: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Gradu handiagoko joera-lerro polinomialen formulak eredu bera erabiliz eraiki daitezke.

Gure datu-multzorako, 2. ordenako joera-lerro polinomialen multzoak hobeto, beraz, formula hauek erabiltzen ari gara:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)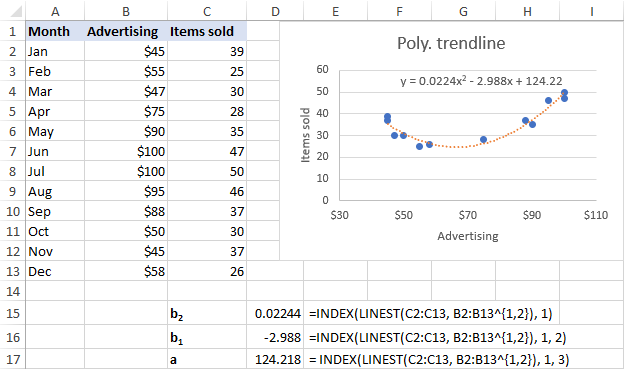

Potentzia-joera-lerroaren ekuazioa eta formulak

Excel-en potentzia-joera-lerroa ekuazio sinple honetan oinarrituta marrazten da:

y = axb

Non a eta b konstanteak dira, eta formula hauekin kalkula daitezke:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

Gure kasuan, formula hauek atsegina da. :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Excel joera-lerroaren ekuazioa okerra da - arrazoiak eta konponketak

Excel-ek joera-lerroa gaizki marraztu duela uste baduzu edo zure grafikoan bistaratzen den joera-lerroaren formula okerra da, hurrengo bi puntuek batzuk bota ditzakete argitu egoera.

Excel-ren joera-lerroaren ekuazioa zuzena da sakabanaketa-diagrametan soilik

Excel-ren joera-lerroaren formulak XY (sakabanaketa) grafikoekin soilik erabili behar dira, zeren eta grafiko honetan bakarrik idazten dituzte biak y-ardatza. eta x ardatza zenbakizko balio gisa irudikatzen dira.

Lerro-diagrametan, zutabeetan eta barra-grafikoetan, zenbakizko balioak y ardatzean bakarrik marrazten dira. X ardatza serie lineal baten bidez adierazten da (1, 2,3,…) ardatzaren etiketak zenbakiak edo testuak diren kontuan hartu gabe. Grafiko hauetan joera-lerroa egiten duzunean, Excel-ek joera-lerroaren formulan suposatzen dituen x balio horiek erabiltzen ditu.

Zenbakiak Excel-ren joera-lerroaren ekuazioan biribiltzen dira

Taulan leku gutxiago okupatzeko, Excel-ek bistaratzen du. oso zifra esanguratsu gutxi joera-lerroaren ekuazio batean. Diseinuari dagokionez polita, nabarmen murrizten du formularen zehaztasuna ekuazioan x balioak eskuz ematen dituzunean.

Konponketa erraza da ekuazioan hamartar gehiago erakustea. Bestela, koefizienteak kalkula ditzakezu zure joera-lerro motari dagokion formula erabiliz, eta formateatu formula-gelaxkak hamartar kopuru nahikoa erakusteko. Horretarako, egin klik Zenbakia taldeko Zenbakia fitxako Hazitu hamartarra botoian.

Horrela, joera-lerro mota desberdinak egin ditzakezu. Excel-en eta lortu haien ekuazioak. Eskerrik asko irakurtzeagatik eta datorren astean gure blogean ikustea espero dut!