Yn y tiwtorial hwn, fe welwch ddisgrifiad manwl o'r holl opsiynau trendline sydd ar gael yn Excel a phryd i'w defnyddio. Byddwch hefyd yn dysgu sut i arddangos hafaliad tueddiad mewn siart a dod o hyd i oleddf y duedd.

Mae'n hawdd iawn ychwanegu llinell duedd yn Excel. Yr unig her wirioneddol yw dewis y math o linell duedd sy'n cyfateb orau i'r math o ddata rydych chi'n ei ddadansoddi. Yn y tiwtorial hwn, fe welwch ddisgrifiad manwl o'r holl opsiynau trendline sydd ar gael yn Excel a phryd i'w defnyddio. Os ydych chi'n chwilio am sut i fewnosod llinell duedd mewn siart Excel, edrychwch ar y tiwtorial cysylltiedig uchod.

Mathau o dueddiadau Excel

Wrth ychwanegu llinell duedd yn Excel , mae gennych 6 opsiwn gwahanol i ddewis ohonynt. Yn ogystal, mae Microsoft Excel yn caniatáu arddangos hafaliad tueddiad a gwerth sgwâr-R mewn siart:

• Mae hafaliad tueddiad yn fformiwla sy'n dod o hyd i linell sy'n cyd-fynd orau â'r pwyntiau data.
• Mae gwerth sgwar R yn mesur dibynadwyedd y duedd - po agosaf yw R2 at 1, y gorau yw'r llinell duedd i'r data.

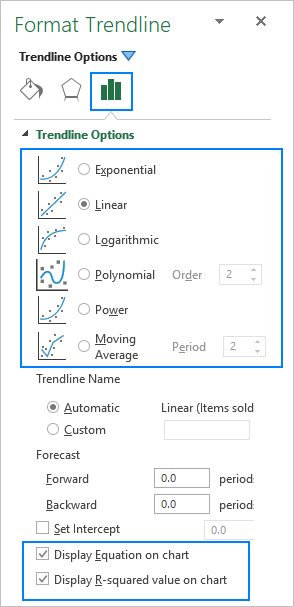
Isod, fe welwch ddisgrifiad byr o bob math o linell duedd gydag enghreifftiau siart.

Llinell duedd linellol

Y llinell duedd llinol sydd orau i fod. a ddefnyddir gyda setiau data llinol pan fydd y pwyntiau data mewn siart yn ymdebygu i linell syth. Yn nodweddiadol, mae tueddiad llinellol yn disgrifio codiad neu gwymp parhausdros amser.

Er enghraifft, mae'r duedd linellol ganlynol yn dangos cynnydd cyson mewn gwerthiant dros 6 mis. Ac mae gwerth R2 o 0.9855 yn dangos cydweddiad eithaf da o'r gwerthoedd tueddiad amcangyfrifedig i'r data gwirioneddol.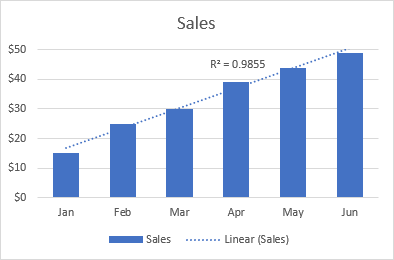

Tueddlin esbonyddol

Llinell grom yw'r duedd esbonyddol sy'n dangos codiad neu ostyngiad mewn gwerthoedd data ar gyfradd gynyddol, felly mae'r llinell fel arfer yn fwy crwm ar un ochr. Defnyddir y math hwn o dueddiad yn aml mewn gwyddorau, er enghraifft i ddelweddu twf poblogaeth ddynol neu leihad mewn poblogaethau bywyd gwyllt.

Sylwer na ellir creu tueddiad esbonyddol ar gyfer data sy'n cynnwys seroau neu werthoedd negyddol.

Enghraifft dda o gromlin esbonyddol yw'r dirywiad yn holl boblogaeth y teigrod gwyllt ar y ddaear.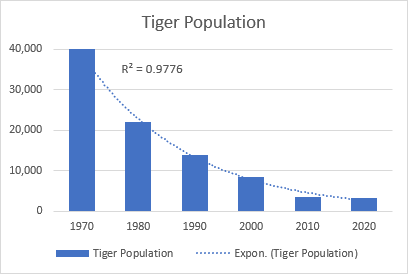

Llinell duedd logarithmig

Yn gyffredinol, defnyddir y llinell ffit orau logarithmig i blotio data sy'n cynyddu neu'n gostwng yn gyflym ac yna'n gwastatáu. Gall gynnwys gwerthoedd cadarnhaol a negyddol.

Gallai enghraifft o dueddiad logarithmig fod yn gyfradd chwyddiant, sy'n mynd yn uwch i ddechrau ond yn sefydlogi ymhen ychydig.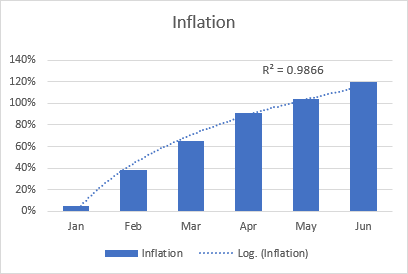

Tueddlin polynomaidd

Mae'r dueddlin gromliniol polynomaidd yn gweithio'n dda ar gyfer setiau data mawr gyda gwerthoedd osgiliadol sydd â mwy nag un codiad a chwymp.

Yn gyffredinol, mae polynomial yn cael ei ddosbarthu gan y gradd yr esboniwr mwyaf. Gall graddau'r duedd polynomaiddcael ei bennu hefyd gan nifer y troadau ar graff. Yn nodweddiadol, mae gan linell duedd polynomaidd cwadratig un tro (bryn neu ddyffryn), mae gan polynomial ciwbig 1 neu 2 dro, ac mae gan polynomial chwartig hyd at 3 tro.

Wrth ychwanegu llinell duedd polynomaidd mewn siart Excel, rydych yn nodi'r radd drwy deipio'r rhif cyfatebol yn y blwch Gorchymyn ar y cwarel Fformat Trendline , sef 2 yn ddiofyn: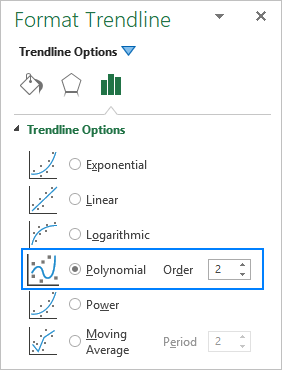

Er enghraifft, y duedd polynomaidd cwadratig yn amlwg ar y graff canlynol sy'n dangos y berthynas rhwng yr elw a nifer y blynyddoedd y mae'r cynnyrch wedi bod ar y farchnad: cynnydd yn y dechrau, brig yn y canol a disgyn yn agos at y diwedd.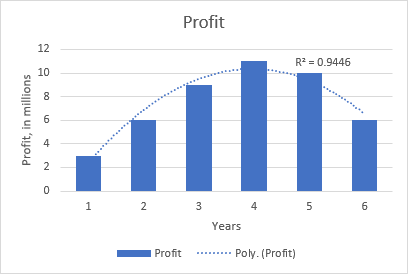

Llinell duedd pŵer

Mae'r llinell duedd pŵer yn debyg iawn i'r gromlin esbonyddol, dim ond arc mwy cymesur sydd ganddi. Fe'i defnyddir yn gyffredin i blotio mesuriadau sy'n cynyddu ar gyfradd benodol.

Ni ellir ychwanegu llinell duedd pŵer at siart Excel sy'n cynnwys gwerthoedd sero neu negatif.

Fel enghraifft, gadewch i ni luniadu a llinell duedd pŵer i ddelweddu'r gyfradd adwaith cemegol. Sylwch ar werth sgwar R o 0.9918, sy'n golygu bod ein llinell duedd yn cyd-fynd â'r data bron yn berffaith.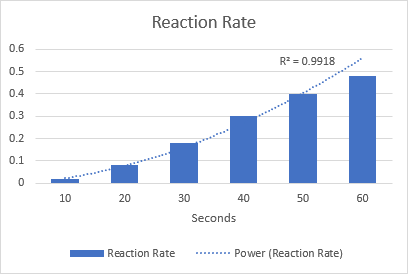

Llinell duedd gyfartalog symudol

Pan fydd y pwyntiau data yn eich siart yn mynd yn fwy ac yn isel, gall llinell duedd gyfartalog symudol lyfnhau'r amrywiadau eithafol mewn gwerthoedd data i ddangos patrwm yn gliriach. Ar gyfer hyn, mae Excel yn cyfrifo'rcyfartaledd symudol y nifer o gyfnodau a nodir gennych (2 yn ddiofyn) ac yn rhoi'r gwerthoedd cyfartalog hynny fel pwyntiau yn y llinell. Po uchaf yw'r gwerth Cyfnod , y llyfnaf yw'r llinell.

Enghraifft ymarferol dda yw defnyddio'r duedd cyfartaledd symudol i ddatgelu amrywiadau mewn pris stoc a fyddai fel arall yn anodd i'w gweld.

Am ragor o wybodaeth, gweler: Sut i ychwanegu llinell duedd gyfartalog symudol at siart Excel.

Haliadau a fformiwlâu tueddlinau Excel

Mae'r adran hon yn disgrifio'r hafaliadau y mae Excel yn eu defnyddio ar gyfer gwahanol fathau o dueddiadau. Nid oes yn rhaid i chi adeiladu'r fformiwlâu hyn â llaw, dim ond dweud wrth Excel i ddangos yr hafaliad trendline mewn siart.

Hefyd, byddwn yn trafod y fformiwla i ddarganfod goledd llinell duedd a chyfernodau eraill. Mae'r fformiwlâu yn cymryd bod gennych 2 set o newidynnau: newidyn annibynnol x a newidyn dibynnol y . Yn eich taflenni gwaith, gallwch ddefnyddio'r fformiwlâu hyn i gael y gwerthoedd y a ragfynegir ar gyfer unrhyw werthoedd penodol o x .

Er cysondeb, byddwn yn defnyddio'r un data gosod gyda gwerthoedd ychydig yn amrywio ar gyfer yr holl enghreifftiau. Fodd bynnag, cofiwch mai dim ond at ddibenion arddangos y mae hyn. Yn eich taflenni gwaith go iawn, dylech ddewis y math o linell duedd sy'n cyfateb i'ch math o ddata.

Nodyn pwysig! Dim ond gyda siartiau gwasgariad XY y dylid defnyddio'r fformiwlâu tueddiad oherwydd hyn yn unigplotiau siart y ddwy echelin x ac y fel gwerthoedd rhifol. Am ragor o wybodaeth, gweler Pam y gall hafaliad tueddiad Excel fod yn anghywir.

Haliad tueddiad llinellol a fformiwlâu

Mae'r hafaliad tueddiadau llinol yn defnyddio'r dulliau sgwariau lleiaf i chwilio am y llethr a rhyng-gipio cyfernodau fel:

y = bx + a

Ble:

• b yw'r llethr o linell duedd.
• a yw'r rhyngdoriad y- , sef y gwerth cymedrig disgwyliedig o y pan mae pob x yn hafal i 0. Ar siart, dyma'r pwynt lle mae'r llinell duedd yn croesi'r echel y .

Ar gyfer atchweliad llinol, mae Microsoft Excel yn darparu swyddogaethau arbennig i gael y cyfernodau llethr a rhyngdoriad.

Cledd y llinell duedd

b: =SLOPE(y,x)

Y-intercept

a: =INTERCEPT(y,x)

Gan dybio mai'r ystod x yw B2:B13 a'r amrediad y yw C2:C13, mae'r fformiwlâu bywyd go iawn yn mynd fel a ganlyn:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Gellir cyflawni'r un canlyniadau drwy ddefnyddio'r ffwythiant LINEST fel fformiwla arae . Ar gyfer hyn, dewiswch 2 gell gyfagos yn yr un rhes, rhowch y fformiwla a gwasgwch Ctrl + Shift + Enter i'w chwblhau:

=LINEST(C2:C13,B2:B13)

Fel y dangosir yn y sgrin isod, mae'r llethr a'r rhyngdoriad mae'r cyfernodau a ddychwelir gan y fformiwlâu yn cyd-fynd yn berffaith â'r cyfernodau yn yr hafaliad tueddiad llinellol a ddangosir yn y siart, dim ond yr olaf sy'n cael eu talgrynnu i 4 lle degol: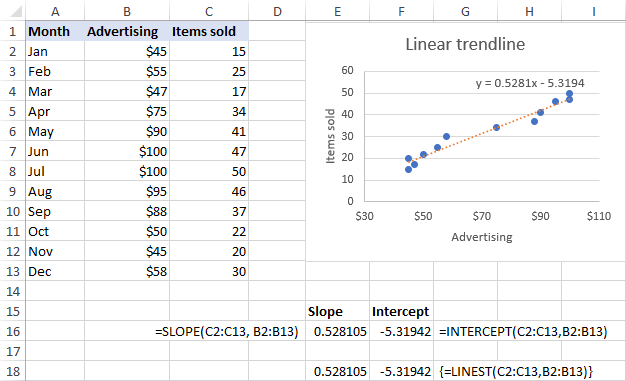

Haliad tueddiad esbonyddol a fformiwlâu

Ar gyfer y duedd esbonyddol, mae Excel yn defnyddio'r hafaliad canlynol:

y = aebx

Ble a a b Cyfnodau cyfrifedig yw ac e yw'r cysonyn mathemategol e (sylfaen y logarithm naturiol).

Gellir cyfrifo'r cyfernodau trwy ddefnyddio'r fformiwlâu generig hyn:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2)) <3

b: =INDEX(LINEST(LN(y), x), 1)

Ar gyfer ein set ddata sampl, mae'r fformiwlâu yn cymryd y siâp canlynol:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Hafaliad tueddiad logarithmig a fformiwlâu

Dyma'r hafaliad tueddiad logarithmig yn Excel:

y = a*ln(x)+b

Lle a a b yn gysonion a ln yw'r ffwythiant logarithm naturiol.

I gael y cysonion, defnyddiwch y fformiwlâu generig hyn, sydd ond yn wahanol yn y ddadl olaf:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Ar gyfer ein set ddata sampl, rydym yn defnyddio'r rhai hyn:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Hafaliad tueddiadau polynomaidd a fformiwlâu

I gyfrifo'r duedd aml-linell, mae Excel yn defnyddio'r hafaliad hwn:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Lle b ₁ … b ₆ a a yn gysonion.

Yn dibynnu ar raddau eich tueddiad polynomaidd, defnyddiwch un o'r setiau canlynol o fformiwlâu i gael y cysonion.

Tueddlin polynomaidd cwadratic (2il drefn)

Haliad: y = b ₂ x2+ b ₁ x + a<3

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Ciwbig (3ydd gorchymyn) llinell duedd aml-liw

Hafaliad: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Gellir adeiladu'r fformiwlâu ar gyfer llinellau tueddiadau polynomaidd gradd uwch drwy ddefnyddio'r un patrwm.

Ar gyfer ein set ddata, y gyfres o linellau tueddiadau polynomaidd 2il orchymyn yn well, felly rydym yn defnyddio'r fformiwlâu hyn:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)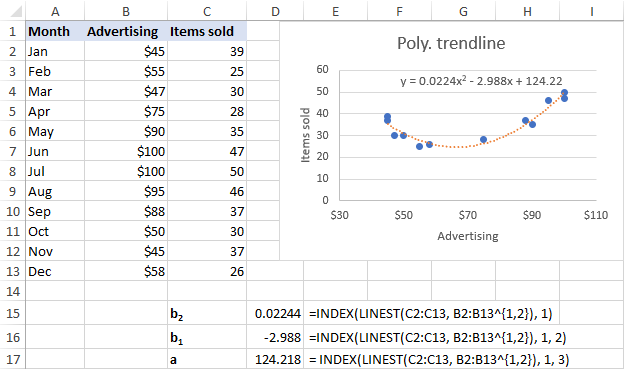

Haliad tueddiad pŵer a fformiwlâu

Tynnir llinell duedd pŵer yn Excel yn seiliedig ar yr hafaliad syml hwn:

y = axb

Ble a a <1 Mae>b yn gysonion, y gellir eu cyfrifo gyda'r fformiwlâu hyn:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

Yn ein hachos ni, mae'r fformiwlâu canlynol yn gweithio'n dda :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Mae hafaliad trendline Excel yn anghywir - rhesymau a chyfyngiadau

Os ydych chi'n meddwl bod Excel wedi tynnu llinell duedd yn anghywir neu os yw'r fformiwla dueddlin a ddangosir yn eich siart yn anghywir, efallai y bydd y ddau bwynt canlynol yn colli rhai golau ar y sefyllfa.

Mae hafaliad trendline Excel yn gywir mewn siartiau gwasgariad yn unig

Dylid defnyddio fformiwlâu tueddlin Excel gyda graffiau XY (gwasgariad) yn unig oherwydd dim ond yn y siart hwn teipiwch y ddwy echelin-y ac echelin-x yn cael eu plotio fel gwerthoedd rhifol.

Mewn siartiau llinell, graffiau colofn a bar, mae gwerthoedd rhifol yn cael eu plotio ar yr echelin-y yn unig. Cynrychiolir yr echelin-x gan gyfres linol (1, 2,3,…) ni waeth a yw'r labeli echelin yn rhifau neu'n destun. Pan fyddwch chi'n gwneud llinell duedd yn y siartiau hyn, mae Excel yn defnyddio'r gwerthoedd-x tybiedig hynny yn y fformiwla trendline.

Mae'r niferoedd wedi'u talgrynnu yn hafaliad trendline Excel

I feddiannu llai o le yn y siart, mae Excel yn dangos ychydig iawn o ddigidau arwyddocaol mewn hafaliad tueddiad. Yn braf o ran dyluniad, mae'n lleihau cywirdeb y fformiwla'n sylweddol pan fyddwch chi'n cyflenwi gwerthoedd x yn yr hafaliad â llaw.

Atgyweiriad hawdd yw dangos mwy o leoedd degol yn yr hafaliad. Fel arall, gallwch gyfrifo'r cyfernodau trwy ddefnyddio fformiwla sy'n cyfateb i'ch math o linell duedd, a fformatio'r celloedd fformiwla fel eu bod yn dangos nifer digonol o leoedd degol. Ar gyfer hyn, cliciwch ar y botwm Cynyddu Degol ar y tab Cartref yn y grŵp Rhif .

Dyna sut y gallwch chi wneud gwahanol fathau o linell duedd yn Excel a chael eu hafaliadau. Diolch am ddarllen a gobeithio y gwelwn ni chi ar ein blog wythnos nesaf! 3>