Dans ce tutoriel, vous trouverez la description détaillée de toutes les options de ligne de tendance disponibles dans Excel et quand les utiliser. Vous apprendrez également comment afficher une équation de ligne de tendance dans un graphique et trouver la pente de la ligne de tendance.

Il est très facile d'ajouter une ligne de tendance dans Excel. Le seul véritable défi est de choisir le type de ligne de tendance qui correspond le mieux au type de données que vous analysez. Dans ce tutoriel, vous trouverez la description détaillée de toutes les options de ligne de tendance disponibles dans Excel et quand les utiliser. Si vous cherchez comment insérer une ligne de tendance dans un graphique Excel, veuillez consulter le tutoriel ci-dessus.

Types de lignes de tendance Excel

Lorsque vous ajoutez une ligne de tendance dans Excel, vous avez le choix entre 6 options différentes. En outre, Microsoft Excel permet d'afficher l'équation de la ligne de tendance et la valeur R au carré dans un graphique :

• Équation de la ligne de tendance est une formule qui permet de trouver la ligne qui correspond le mieux aux points de données.
• Valeur R-carré mesure la fiabilité de la ligne de tendance - plus R2 est proche de 1, mieux la ligne de tendance s'adapte aux données.

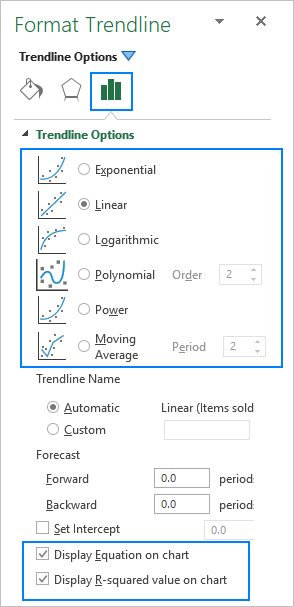
Vous trouverez ci-dessous une brève description de chaque type de ligne de tendance avec des exemples de graphiques.

Ligne de tendance linéaire

La ligne de tendance linéaire est à utiliser avec des ensembles de données linéaires lorsque les points de données d'un graphique ressemblent à une ligne droite. En général, une ligne de tendance linéaire décrit une hausse ou une baisse continue dans le temps.

Par exemple, la ligne de tendance linéaire suivante montre une augmentation régulière des ventes sur 6 mois. Et la valeur R2 de 0,9855 indique une assez bonne adéquation des valeurs estimées de la ligne de tendance aux données réelles.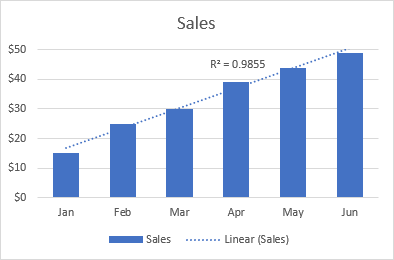

Ligne de tendance exponentielle

La ligne de tendance exponentielle est une ligne courbe qui illustre une augmentation ou une diminution des valeurs des données à un rythme croissant, c'est pourquoi la ligne est généralement plus incurvée d'un côté. Ce type de ligne de tendance est souvent utilisé dans les sciences, par exemple pour visualiser la croissance de la population humaine ou le déclin des populations sauvages.

Veuillez noter qu'une ligne de tendance exponentielle ne peut pas être créée pour les données qui contiennent des zéros ou des valeurs négatives.

Un bon exemple de courbe exponentielle est la diminution de la population totale de tigres sauvages sur la planète.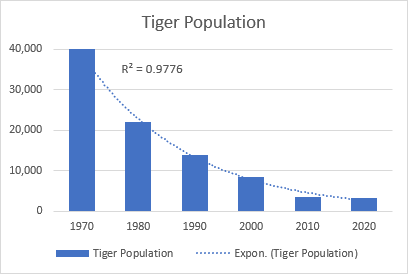

Ligne de tendance logarithmique

La droite logarithmique de meilleure adéquation est généralement utilisée pour tracer des données qui augmentent ou diminuent rapidement, puis se stabilisent. Elle peut inclure des valeurs positives et négatives.

Un exemple de ligne de tendance logarithmique peut être le taux d'inflation, qui augmente d'abord mais se stabilise ensuite.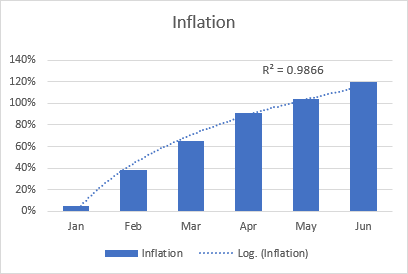

Ligne de tendance polynomiale

La ligne de tendance curviligne polynomiale fonctionne bien pour les grands ensembles de données avec des valeurs oscillantes qui ont plus d'une montée et d'une descente.

En général, un polynôme est classé en fonction du degré du plus grand exposant. Le degré de la ligne de tendance d'un polynôme peut également être déterminé par le nombre de courbes sur un graphique. Typiquement, une ligne de tendance d'un polynôme quadratique a une courbe (colline ou vallée), un polynôme cubique a 1 ou 2 courbes, et un polynôme quartique a jusqu'à 3 courbes.

Lorsque vous ajoutez une ligne de tendance polynomiale dans un graphique Excel, vous spécifiez le degré en tapant le nombre correspondant dans le champ Commandez sur le Format de la ligne de tendance qui est de 2 par défaut :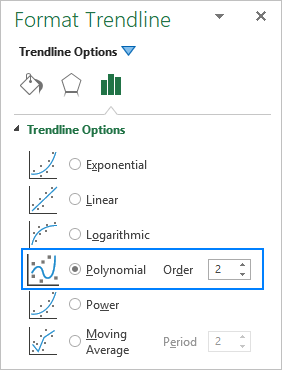

Par exemple, la tendance polynomiale quadratique est évidente sur le graphique suivant qui montre la relation entre le bénéfice et le nombre d'années pendant lesquelles le produit a été sur le marché : hausse au début, pic au milieu et baisse vers la fin.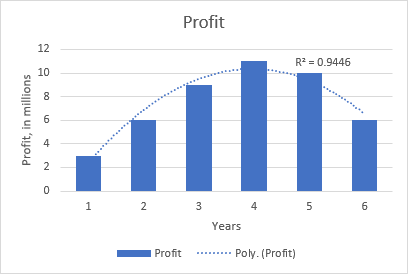

Ligne de tendance de puissance

La ligne de tendance de la puissance est très similaire à la courbe exponentielle, sauf qu'elle a un arc plus symétrique. Elle est couramment utilisée pour tracer des mesures qui augmentent à un certain rythme.

Une ligne de tendance de puissance ne peut pas être ajoutée à un graphique Excel qui contient des valeurs nulles ou négatives.

À titre d'exemple, dessinons une ligne de tendance pour visualiser le taux de réaction chimique. Notez la valeur R-carré de 0,9918, ce qui signifie que notre ligne de tendance s'adapte presque parfaitement aux données.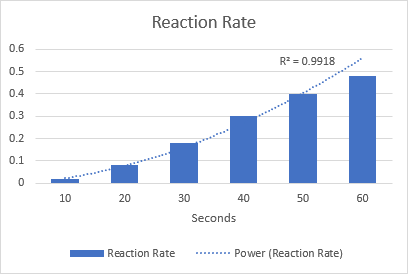

Ligne de tendance de la moyenne mobile

Lorsque les points de données de votre graphique ont beaucoup de hauts et de bas, une ligne de tendance de la moyenne mobile peut lisser les fluctuations extrêmes des valeurs de données pour montrer un modèle plus clairement. Pour cela, Excel calcule la moyenne mobile du nombre de périodes que vous spécifiez (2 par défaut) et place ces valeurs moyennes comme points dans la ligne. Période Plus la valeur est élevée, plus la ligne est lisse.

Un bon exemple pratique est l'utilisation de la ligne de tendance de la moyenne mobile pour révéler les fluctuations du cours d'une action qui seraient autrement difficiles à observer.

Pour plus d'informations, veuillez consulter : Comment ajouter une ligne de tendance de moyenne mobile à un graphique Excel.

Équations et formules Excel pour les lignes de tendance

Cette section décrit les équations qu'Excel utilise pour différents types de lignes de tendance. Vous n'avez pas à construire ces formules manuellement, il suffit de demander à Excel d'afficher l'équation de ligne de tendance dans un graphique.

Nous aborderons également la formule permettant de trouver la pente d'une ligne de tendance et d'autres coefficients. Les formules supposent que vous disposez de deux ensembles de variables : variable indépendante x et variable dépendante y Dans vos feuilles de calcul, vous pouvez utiliser ces formules pour obtenir les valeurs prédites. y pour toute valeur donnée de x .

Pour des raisons de cohérence, nous utiliserons le même ensemble de données avec des valeurs légèrement différentes pour tous les exemples. Cependant, n'oubliez pas qu'il s'agit uniquement d'une démonstration. Dans vos feuilles de travail réelles, vous devez choisir le type de ligne de tendance correspondant à votre type de données.

Remarque importante : les formules de ligne de tendance ne doivent être utilisées qu'avec Graphiques en nuage de points XY parce que seul ce graphique trace les deux x et y Pour plus d'informations, veuillez consulter la section Pourquoi l'équation de la ligne de tendance d'Excel peut être erronée.

Équation et formules de la ligne de tendance linéaire

L'équation de la ligne de tendance linéaire utilise les méthodes des moindres carrés pour rechercher le pente et intercepter des coefficients tels que :

Où :

• b est le pente d'une ligne de tendance.
• a est le Intersection des ordonnées qui est la valeur moyenne attendue de y lorsque tous les x sont égales à 0. Sur un graphique, c'est le point où la ligne de tendance croise la ligne de base. y axe.

Pour la régression linéaire, Microsoft Excel fournit des fonctions spéciales pour obtenir les coefficients de pente et d'interception.

Pente de la ligne de tendance

b : =SLOPE(y,x)

Intersection des Y

a : =INTERCEPT(y,x)

En supposant que le x est B2:B13 et la y est C2:C13, les formules de la vie réelle sont les suivantes :

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Les mêmes résultats peuvent être obtenus en utilisant la fonction LINEST en tant que formule matricielle Pour cela, sélectionnez 2 cellules adjacentes dans la même ligne, entrez la formule et appuyez sur Ctrl + Shift + Enter pour la compléter :

=LINEST(C2:C13,B2:B13)

Comme le montre la capture d'écran ci-dessous, les coefficients de pente et d'interception renvoyés par les formules sont parfaitement conformes aux coefficients de l'équation de la ligne de tendance linéaire affichée dans le graphique, sauf que ces derniers sont arrondis à 4 décimales :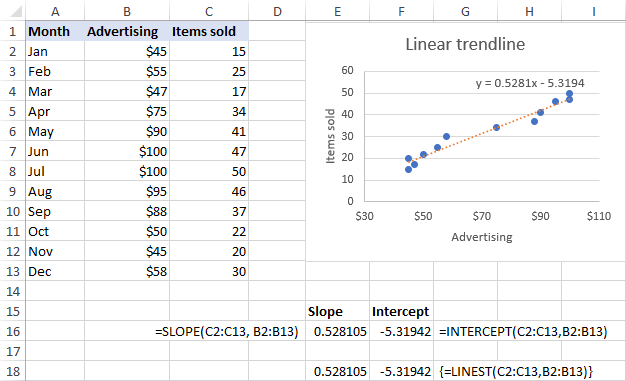

Équation et formules de la ligne de tendance exponentielle

Pour la ligne de tendance exponentielle, Excel utilise l'équation suivante :

Où a et b sont des coefficients calculés et e est la constante mathématique e (la base du logarithme naturel).

Les coefficients peuvent être calculés à l'aide de ces formules génériques :

a : =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b : =INDEX(LINEST(LN(y), x), 1)

Pour notre échantillon de données, les formules prennent la forme suivante :

a : =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b : =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Équation et formules de la ligne de tendance logarithmique

Voici l'équation de la ligne de tendance logarithmique dans Excel :

Où a et b sont des constantes et ln est la fonction du logarithme naturel.

Pour obtenir les constantes, utilisez ces formules génériques, qui ne diffèrent que par le dernier argument :

a : =INDEX(LINEST(y, LN(x)), 1)

b : =INDEX(LINEST(y, LN(x)), 1, 2)

Pour notre échantillon de données, nous utilisons ceux-là :

a : =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b : =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Équation et formules de la ligne de tendance polynomiale

Pour calculer la ligne de tendance polynomiale, Excel utilise cette équation :

Où b ₁ ... b ₆ et a sont des constantes.

Selon le degré de votre ligne de tendance polynomiale, utilisez l'un des ensembles de formules suivants pour obtenir les constantes.

Ligne de tendance polynomiale quadratique (2e ordre)

Équation : y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a : =INDEX(LINEST(y, x^{1,2}), 1, 3)

Ligne de tendance polynomiale cubique (3e ordre)

Équation : y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a : =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Les formules pour les lignes de tendance polynomiales de degré supérieur peuvent être construites en utilisant le même modèle.

Pour notre ensemble de données, la ligne de tendance polynomiale d'ordre 2 est plus adaptée, nous utilisons donc ces formules :

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)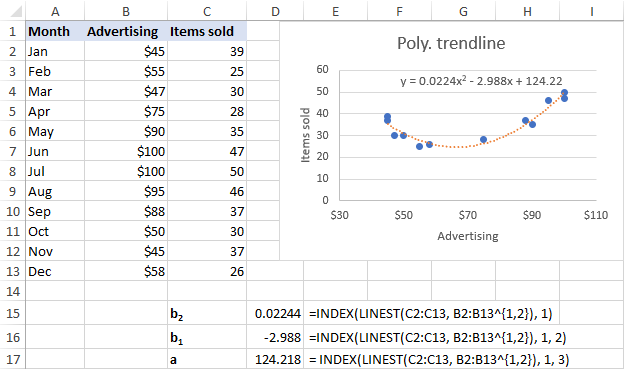

Équation et formules de la ligne de tendance de puissance

Une ligne de tendance dans Excel est dessinée sur la base de cette simple équation :

Où a et b sont des constantes, qui peuvent être calculées à l'aide de ces formules :

a : =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2)))

b : =INDEX(LINEST(LN(y), LN(x),,), 1)

Dans notre cas, les formules suivantes fonctionnent à merveille :

a : =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2)))

b : =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

L'équation de la ligne de tendance d'Excel est erronée - raisons et solutions

Si vous pensez qu'Excel a dessiné une ligne de tendance de manière incorrecte ou que la formule de la ligne de tendance affichée dans votre graphique est erronée, les deux points suivants peuvent vous éclairer sur la situation.

L'équation de la ligne de tendance d'Excel est correcte uniquement dans les diagrammes de dispersion.

Les formules Excel de lignes de tendance ne doivent être utilisées qu'avec des graphiques XY (en nuage de points) car, dans ce type de graphique, l'axe des y et l'axe des x sont tous deux tracés sous forme de valeurs numériques.

Dans les graphiques linéaires, les graphiques à colonnes et les graphiques à barres, les valeurs numériques sont tracées uniquement sur l'axe des y. L'axe des x est représenté par une série linéaire (1, 2, 3,...), que les étiquettes des axes soient des chiffres ou du texte. Lorsque vous créez une ligne de tendance dans ces graphiques, Excel utilise ces valeurs x supposées dans la formule de la ligne de tendance.

Les chiffres sont arrondis dans l'équation des courbes de tendance d'Excel.

Pour occuper moins d'espace dans le graphique, Excel affiche très peu de chiffres significatifs dans une équation de ligne de tendance. Agréable en termes de conception, cela réduit considérablement la précision de la formule lorsque vous fournissez manuellement les valeurs x dans l'équation.

Une solution simple consiste à afficher plus de décimales dans l'équation. Vous pouvez également calculer les coefficients en utilisant une formule correspondant à votre type de ligne de tendance et formater les cellules de la formule de manière à ce qu'elles affichent un nombre suffisant de décimales. Pour cela, il suffit de cliquer sur le bouton Augmenter la décimale sur le bouton Accueil dans l'onglet Numéro groupe.

C'est ainsi que vous pouvez créer différents types de lignes de tendance dans Excel et obtenir leurs équations. Je vous remercie de votre lecture et j'espère vous voir sur notre blog la semaine prochaine !