En ĉi tiu lernilo, vi trovos la detalan priskribon de ĉiuj tendencaj elektoj disponeblaj en Excel kaj kiam uzi ilin. Vi ankaŭ lernos kiel montri tendenclinian ekvacion en diagramo kaj trovi la deklivon de tendenclinio.

Estas tre facile aldoni tendenclinion en Excel. La sola vera defio estas elekti la tendencan tipon, kiu plej bone respondas al la tipo de datumoj, kiujn vi analizas. En ĉi tiu lernilo, vi trovos la detalan priskribon de ĉiuj tendencaj elektoj disponeblaj en Excel kaj kiam uzi ilin. Se vi serĉas kiel enmeti tendencon en Excel-diagramo, bonvolu kontroli la ĉi-supran ligitan lernilon.

Excel-tendencaj tipoj

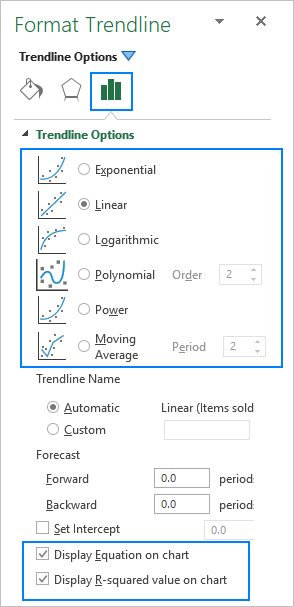
Kiam aldonos tendenclinion en Excel. , vi havas 6 malsamajn eblojn por elekti. Aldone, Microsoft Excel permesas montri tendencan ekvacion kaj R-kvadratan valoron en diagramo:

• Tendlinia ekvacio estas formulo, kiu trovas linion, kiu plej bone konvenas al la datumaj punktoj.
• R-kvadrata valoro mezuras la tendencan fidindecon - ju pli R2 estas al 1, des pli bone la tendenclinio konvenas al la datumoj.

Malsupre, vi trovos mallongan priskribon de ĉiu tendenca tipo kun diagramekzemploj.

Linia tendenca

La linia tendenca linio estas plej bone esti uzata kun liniaj datumserioj kiam la datenpunktoj en diagramo similas rektan linion. Tipe, linia tendenca linio priskribas daŭran pliiĝon aŭ falonkun la tempo.

Ekzemple, la sekva lineara tendenco montras konstantan pliiĝon de vendoj dum 6 monatoj. Kaj la R2-valoro de 0.9855 indikas sufiĉe bonan taŭgecon de la taksitaj tendencaj valoroj al la realaj datumoj.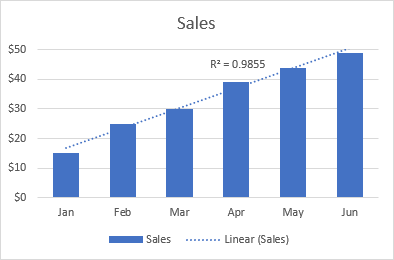

Eksponenta tendenclinio

La eksponenta tendenclinio estas kurba linio, kiu ilustras pliiĝon aŭ falon de datenvaloroj kun pliiĝanta rapideco, tial la linio estas kutime pli kurba ĉe unu flanko. Ĉi tiu tendenclinio estas ofte uzata en sciencoj, ekzemple por bildigi homan loĝantarkreskon aŭ malkreskon en sovaĝaj populacioj.

Bonvolu noti, ke eksponenta tendenca linio ne povas esti kreita por datumoj kiuj enhavas nulojn aŭ negativajn valorojn.

Bona ekzemplo de eksponenta kurbo estas la kadukiĝo de la tuta sovaĝa tigropopulacio sur la tero.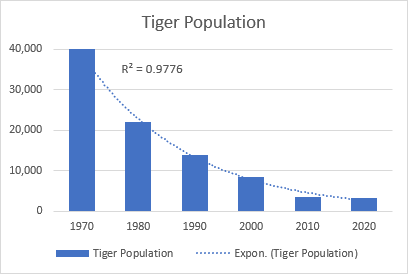

Logaritma tendenclinio

La logaritma plej taŭga linio estas ĝenerale uzata por bildigi datumojn, kiuj rapide pliiĝas aŭ malpliiĝas kaj poste ebeniĝas. Ĝi povas inkluzivi kaj pozitivajn kaj negativajn valorojn.

Ekzemplo de logaritma tendenco povas esti inflacia indico, kiu unue pliiĝas sed post iom da tempo stabiligas.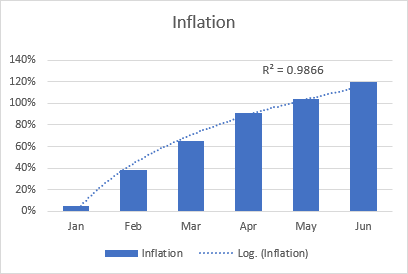

Polinoma tendenclinio

La polinoma kurblinia tendenclinio funkcias bone por grandaj datumaroj kun oscilaj valoroj kiuj havas pli ol unu altiĝon kaj falon.

Ĝenerale, polinomo estas klasifikita per la grado de la plej granda eksponento. La grado de la polinoma tendenclinio povasankaŭ estu determinita per la nombro da kurboj sur grafeo. Tipe, kvadrata polinoma tendenclinio havas unu kurbiĝon (monteto aŭ valo), kuba polinomo havas 1 aŭ 2 kurbojn, kaj kvarta polinomo havas ĝis 3 kurbojn.

Aldonante polinoman tendenclinion en Excel-diagramo, vi specifigas la gradon tajpante la respondan nombron en la skatolo Ordo sur la panelo Format Tendenco , kiu estas 2 defaŭlte: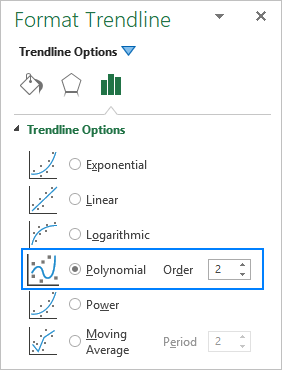

Ekzemple, la kvadrata polinoma tendenco evidentiĝas sur la sekva grafikaĵo, kiu montras la rilaton inter la profito kaj la nombro da jaroj, kiujn la produkto estis sur la merkato: pliiĝo komence, pinto en la mezo kaj malaltiĝo proksime de la fino.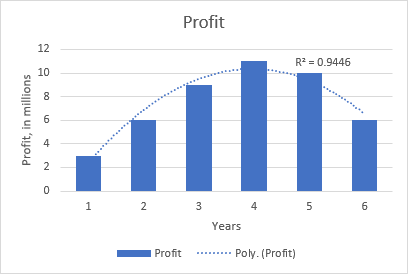

Potenca tendenco

La potenca tendenca linio estas tre simila al la eksponenta kurbo, nur ĝi havas pli simetrian arkon. Ĝi estas kutime uzata por bildigi mezurojn, kiuj pliiĝas je certa rapideco.

Potenca tendenclinio ne povas esti aldonita al Excel-diagramo, kiu enhavas nul aŭ negativajn valorojn.

Ekzemple, ni desegnu potenca tendenco por bildigi la kemian reakcian rapidecon. Notu la R-kvadratan valoron de 0.9918, kio signifas, ke nia tendenco konvenas al la datumoj preskaŭ perfekte.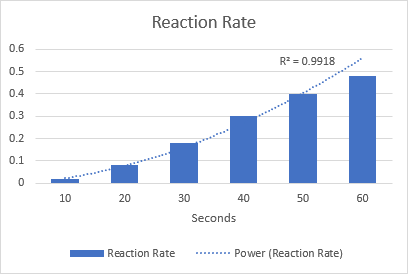

Moviĝanta averaĝa tendenco

Kiam la datumpunktoj en via diagramo havas multajn altiĝojn kaj malsupreniĝojn, moviĝanta averaĝa tendenco povas glatigi la ekstremajn fluktuojn en datumvaloroj por montri ŝablonon pli klare. Por ĉi tio, Excel kalkulas lamovanta mezumo de la nombro da periodoj kiujn vi specifas (2 defaŭlte) kaj metas tiujn averaĝajn valorojn kiel punktojn en la linio. Ju pli alta la Periodo valoro, des pli glata la linio.

Bona praktika ekzemplo estas uzi la moviĝantan averaĝan tendencan linion por malkaŝi fluktuojn en akcia prezo, kiujn alie estus malfacile observi.

Por pliaj informoj, bonvolu vidi: Kiel aldoni moviĝantan averaĝan tendencon al Excel-diagramo.

Ekvacioj kaj formuloj de Excel-tendenco

Ĉi tiu sekcio priskribas la ekvaciojn kiujn Excel uzas. por malsamaj tendencaj tipoj. Vi ne devas konstrui ĉi tiujn formulojn permane, simple diru al Excel montri la tendencan ekvacion en diagramo.

Ankaŭ ni diskutos la formulon por trovi la deklivon de tendenclinio kaj aliajn koeficientojn. La formuloj supozas, ke vi havas 2 arojn de variabloj: sendependa variablo x kaj dependa variablo y . En viaj laborfolioj, vi povas uzi ĉi tiujn formulojn por akiri la antaŭviditajn y valorojn por iuj donitaj valoroj de x .

Por konsistenco, ni uzos la samajn datumojn. aro kun iomete ŝanĝiĝantaj valoroj por ĉiuj ekzemploj. Tamen bonvolu memori, ke ĝi estas nur por pruvaj celoj. En viaj veraj laborfolioj, vi devus elekti la tendencan tipon respondan al via datumtipo.

Grava noto! La tendencliniaj formuloj devas esti uzataj nur kun XY disaj diagramoj ĉar nur ĉi tiodiagramo reprezentas ambaŭ aksojn x kaj y kiel nombrajn valorojn. Por pliaj informoj, bonvolu vidi Kial Excel-tendenclinia ekvacio eble estas malĝusta.

Linia tendenclinia ekvacio kaj formuloj

La linia tendenclinia ekvacio uzas la metodojn de malplej kvadrataj por serĉi la deklivon kaj interkapto koeficientoj tia ke:

y = bx + a

Kie:

• b estas la deklivo de tendenclinio.
• a estas la y-interkapto , kiu estas la atendata mezvaloro de y kiam ĉiuj x variabloj estas egalaj al 0. Sur diagramo, ĝi estas la punkto kie la tendenclinio transiras la y akson.

Por lineara regreso, Microsoft Excel disponigas specialajn funkciojn por akiri la deklivo kaj interkaptokoeficientoj.

Deklivo de tendenclinio

b: =SLOPE(y,x)

Y-interkapto

a: =INTERCEPT(y,x)

Supozante, ke la x intervalo estas B2:B13 kaj la y intervalo estas C2:C13, la realaj formuloj iras jene:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

La samaj rezultoj povas esti atingitaj uzante la LINEST-funkcion kiel tabelformulo . Por tio, elektu 2 apudajn ĉelojn en la sama vico, enigu la formulon kaj premu Ctrl + Shift + Enter por kompletigi ĝin:

=LINEST(C2:C13,B2:B13)

Kiel montrite en la ekrankopio sube, la deklivo kaj interkapto. koeficientoj redonitaj de la formuloj estas perfekte konformaj al la koeficientoj en la lineara tendenclinia ekvacio montrita en la diagramo, nur ĉi tiuj lastaj estas rondigitaj al 4 dekumaj lokoj: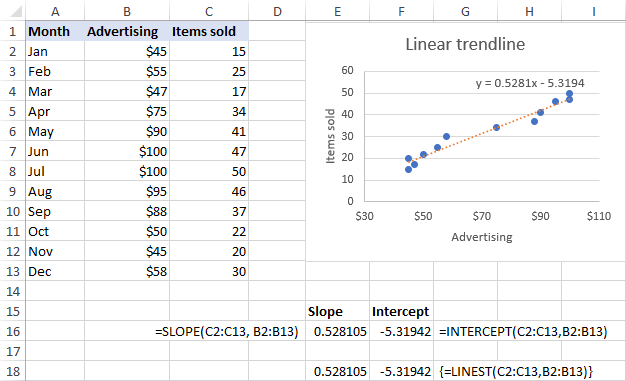

Ekvacio kaj formuloj de eksponenta tendenca linio

Por la eksponenta tendenca linio, Excel uzas la sekvan ekvacion:

y = aebx

Kie a kaj b estas kalkulitaj koeficientoj kaj e estas la matematika konstanto e (la bazo de la natura logaritmo).

La koeficientoj povas esti kalkulitaj uzante ĉi tiujn ĝeneralajn formulojn:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Por nia ekzempla datumaro, la formuloj prenas la jenan formon:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logaritma tendenclinia ekvacio kaj formuloj

Jen la logaritma tendenclinia ekvacio en Excel:

y = a*ln(x)+b

Kie a kaj b estas konstantoj kaj ln estas la natura logaritma funkcio.

Por akiri la konstantojn, uzu ĉi tiujn ĝeneralajn formulojn, kiuj diferencas nur en la lasta argumento:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Por nia ekzempla datumaro, ni uzas ĉi tiujn:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polinoma tendenclinio ekvacio kaj formuloj

Por ellabori la polinoman tendenclinion, Excel uzas ĉi tiun ekvacion:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Kie b ₁ … b ₆ kaj a estas konstantoj.

Dependi de la grado de via polinoma tendenca linio, uzu unu el la sekvaj aroj de formuloj. por ricevi la konstantojn.

Kvadratika (dua ordo) polinoma tendenca linio

Ekvacio: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kuba (3-a ordo) polinoma tendenca linio

Ekvacio: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

La formuloj por pli altaj gradaj polinomaj tendenclinioj povas esti konstruitaj uzante la saman ŝablonon.

Por nia datumaro, la 2-a orda polinomaj tendenclinioj. pli bone, do ni uzas ĉi tiujn formulojn:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)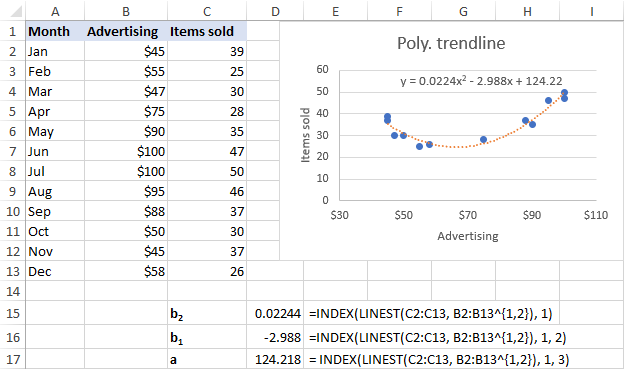

Potenca tendenca ekvacio kaj formuloj

Potenca tendenclinio en Excel estas desegnita surbaze de ĉi tiu simpla ekvacio:

y = axb

Kie a kaj b estas konstantoj, kiuj povas esti kalkulitaj per ĉi tiuj formuloj:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

En nia kazo, la jenaj formuloj funkcias tre bone. :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Ekvacio de Excel-tendenco estas malĝusta - kialoj kaj korektoj

Se vi pensas, ke Excel desegnis tendencan malĝuste aŭ la tendenclinia formulo montrita en via diagramo estas malĝusta, la sekvaj du punktoj povas forĵeti kelkajn lumo pri la situacio.

Ekvacio de Excel-tendenco estas ĝusta nur en disvastigaj diagramoj

Excel-tendencaj formuloj devas esti uzataj nur kun XY (disvastigaj) grafikaĵoj ĉar nur en ĉi tiu diagramo tajpu ambaŭ la y-akson. kaj x-akso estas bildigitaj kiel nombraj valoroj.

En liniodiagramoj, kolumnaj kaj strekgrafikoj, nombraj valoroj estas grafikataj nur sur la y-akso. La x-akso estas reprezentita per lineara serio (1, 2,3,...) sendepende de ĉu la aksaj etikedoj estas nombroj aŭ teksto. Kiam vi faras tendencan linion en ĉi tiuj diagramoj, Excel uzas tiujn supozitajn x-valorojn en la tendenclinia formulo.

Nombroj estas rondigitaj en Excel-tendenca ekvacio

Por okupi malpli da spaco en la diagramo, Excel montras. tre malmultaj signifaj ciferoj en tendenclinia ekvacio. Bela laŭ dezajno, ĝi signife reduktas la precizecon de la formulo kiam vi mane liveras x-valorojn en la ekvacio.

Facila solvo estas montri pli da decimalaj lokoj en la ekvacio. Alternative, vi povas kalkuli la koeficientojn uzante formulon respondan al via tendenca tipo, kaj formi la formulĉelojn tiel ke ili montru sufiĉan nombron da decimalaj lokoj. Por tio, simple alklaku la butonon Multigi Decimal sur la langeto Hejmo en la grupo Nombro .

Tiel vi povas fari malsamajn tendencspecojn. en Excel kaj akiri iliajn ekvaciojn. Mi dankas vin pro legado kaj esperas vidi vin en nia blogo venontsemajne!

3>