ในบทช่วยสอนนี้ คุณจะพบคำอธิบายโดยละเอียดของตัวเลือกเส้นแนวโน้มทั้งหมดที่มีใน Excel และเวลาที่จะใช้ คุณจะได้เรียนรู้วิธีแสดงสมการเส้นแนวโน้มในแผนภูมิและค้นหาความชันของเส้นแนวโน้ม

การเพิ่มเส้นแนวโน้มใน Excel เป็นเรื่องง่ายมาก ความท้าทายเพียงอย่างเดียวคือการเลือกประเภทเส้นแนวโน้มที่สอดคล้องกับประเภทของข้อมูลที่คุณกำลังวิเคราะห์มากที่สุด ในบทช่วยสอนนี้ คุณจะพบคำอธิบายโดยละเอียดของตัวเลือกเส้นแนวโน้มทั้งหมดที่มีใน Excel และเวลาที่จะใช้ หากคุณกำลังมองหาวิธีแทรกเส้นแนวโน้มในแผนภูมิ Excel โปรดดูบทช่วยสอนตามลิงก์ด้านบน

ประเภทเส้นแนวโน้มของ Excel

เมื่อเพิ่มเส้นแนวโน้มใน Excel คุณมี 6 ตัวเลือกที่แตกต่างกันให้เลือก นอกจากนี้ Microsoft Excel ยังอนุญาตให้แสดงสมการเส้นแนวโน้มและค่า R-squared ในแผนภูมิ:

• สมการเส้นแนวโน้ม เป็นสูตรที่ค้นหาเส้นที่เหมาะกับจุดข้อมูลมากที่สุด
• ค่า R-squared วัดความน่าเชื่อถือของเส้นแนวโน้ม - ยิ่ง R2 เข้าใกล้ 1 แสดงว่าเส้นแนวโน้มเหมาะกับข้อมูลมากขึ้น

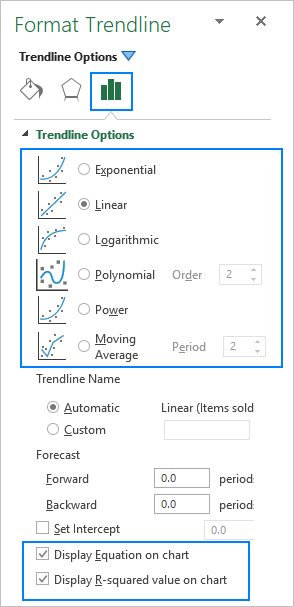
ด้านล่าง คุณจะพบคำอธิบายสั้น ๆ ของเส้นแนวโน้มแต่ละประเภทพร้อมตัวอย่างแผนภูมิ

เส้นแนวโน้มแบบเส้นตรง

เส้นแนวโน้มแบบเส้นเหมาะที่สุด ใช้กับชุดข้อมูลเชิงเส้นเมื่อจุดข้อมูลในแผนภูมิมีลักษณะเป็นเส้นตรง โดยทั่วไป เส้นแนวโน้มเชิงเส้นจะอธิบายถึงการเพิ่มขึ้นหรือลดลงอย่างต่อเนื่องเมื่อเวลาผ่านไป

ตัวอย่างเช่น เส้นแนวโน้มเชิงเส้นต่อไปนี้แสดงยอดขายที่เพิ่มขึ้นอย่างต่อเนื่องในช่วง 6 เดือน และค่า R2 ที่ 0.9855 บ่งชี้ว่าค่าเส้นแนวโน้มที่ประมาณไว้เหมาะสมกับข้อมูลจริงค่อนข้างดี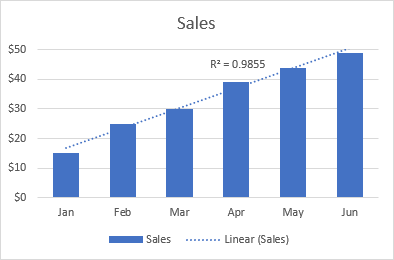

เส้นแนวโน้มแบบเอ็กซ์โพเนนเชียล

เส้นแนวโน้มแบบเอ็กซ์โพเนนเชียลคือเส้นโค้งที่แสดงการเพิ่มขึ้นหรือลดลงของค่าข้อมูลในอัตราที่เพิ่มขึ้น ดังนั้นเส้นมักจะโค้งมากขึ้นที่ด้านใดด้านหนึ่ง เส้นแนวโน้มประเภทนี้มักใช้ในด้านวิทยาศาสตร์ เช่น เพื่อแสดงภาพการเติบโตของประชากรมนุษย์หรือการลดลงของประชากรสัตว์ป่า

โปรดทราบว่าไม่สามารถสร้างเส้นแนวโน้มแบบเอ็กซ์โปเนนเชียลสำหรับข้อมูลที่มีค่าศูนย์หรือค่าลบได้

ตัวอย่างที่ดีของเส้นโค้งเลขชี้กำลังคือการลดลงของประชากรเสือโคร่งทั้งหมดบนโลก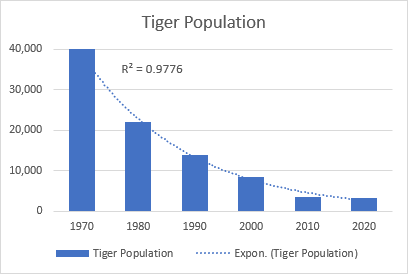

เส้นแนวโน้มลอการิทึม

เส้นแนวโน้มลอการิทึมเหมาะสมที่สุดโดยทั่วไปจะใช้เพื่อลงจุดข้อมูลที่เพิ่มขึ้นหรือลดลงอย่างรวดเร็ว จากนั้นจึงลดระดับลง ซึ่งอาจมีทั้งค่าบวกและค่าลบ

ตัวอย่างของเส้นแนวโน้มแบบลอการิทึมอาจเป็นอัตราเงินเฟ้อ ซึ่งในขั้นแรกจะสูงขึ้น แต่หลังจากนั้นระยะหนึ่งจะคงที่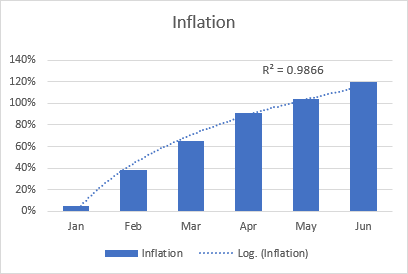

เส้นแนวโน้มพหุนาม

เส้นแนวโน้มโค้งพหุนามทำงานได้ดีสำหรับชุดข้อมูลขนาดใหญ่ที่มีค่าการแกว่งที่มีการขึ้นและลงมากกว่าหนึ่งค่า

โดยทั่วไป พหุนามจะถูกจำแนกตาม ระดับของเลขชี้กำลังที่ใหญ่ที่สุด ระดับของเส้นแนวโน้มพหุนามสามารถยังถูกกำหนดโดยจำนวนของการโค้งบนกราฟ โดยทั่วไป เส้นแนวโน้มพหุนามกำลังสองจะมีหนึ่งโค้ง (เนินหรือหุบเขา) พหุนามลูกบาศก์มี 1 หรือ 2 โค้ง และพหุนามควอตมีมากถึง 3 โค้ง

เมื่อเพิ่มเส้นแนวโน้มพหุนามในแผนภูมิ Excel คุณระบุระดับโดยพิมพ์ตัวเลขที่เกี่ยวข้องในช่อง ลำดับ ในบานหน้าต่าง จัดรูปแบบเส้นแนวโน้ม ซึ่งเป็น 2 ตามค่าเริ่มต้น: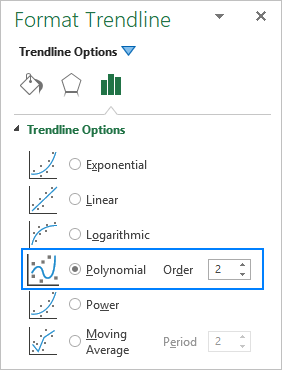

ตัวอย่างเช่น แนวโน้มพหุนามกำลังสอง แสดงให้เห็นได้จากกราฟต่อไปนี้ที่แสดงความสัมพันธ์ระหว่างผลกำไรและจำนวนปีที่ผลิตภัณฑ์อยู่ในตลาด: เพิ่มขึ้นในช่วงเริ่มต้น สูงสุดในช่วงกลาง และลดลงในช่วงใกล้สิ้นสุด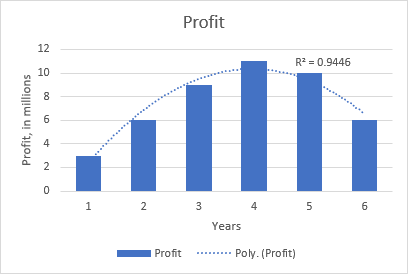

เส้นแนวโน้มกำลัง

เส้นแนวโน้มกำลังคล้ายกับเส้นโค้งเอ็กซ์โปเนนเชียลมาก เพียงแต่มีส่วนโค้งที่สมมาตรมากกว่า โดยทั่วไปจะใช้เพื่อพล็อตการวัดที่เพิ่มขึ้นในอัตราที่แน่นอน

ไม่สามารถเพิ่มเส้นแนวโน้มกำลังลงในแผนภูมิ Excel ที่มีค่าศูนย์หรือค่าลบได้

ตามตัวอย่าง ลองวาด เส้นแนวโน้มกำลังเพื่อให้เห็นภาพอัตราการเกิดปฏิกิริยาเคมี สังเกตค่า R-squared ที่ 0.9918 ซึ่งหมายความว่าเส้นแนวโน้มของเราเหมาะสมกับข้อมูลเกือบจะสมบูรณ์แบบ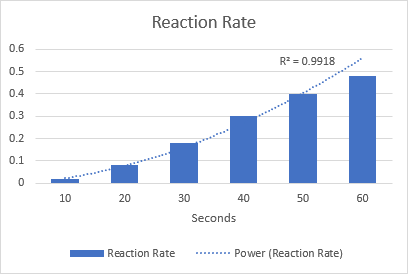

เส้นแนวโน้มค่าเฉลี่ยเคลื่อนที่

เมื่อจุดข้อมูลในแผนภูมิของคุณมีการขึ้นและลงจำนวนมาก เส้นแนวโน้มค่าเฉลี่ยเคลื่อนที่สามารถทำให้ค่าข้อมูลผันผวนมากราบรื่นเพื่อแสดงรูปแบบที่ชัดเจนยิ่งขึ้น สำหรับสิ่งนี้ Excel จะคำนวณค่าเฉลี่ยเคลื่อนที่ของจำนวนงวดที่คุณระบุ (2 โดยค่าเริ่มต้น) และนำค่าเฉลี่ยเหล่านั้นเป็นจุดในบรรทัด ยิ่งค่า ระยะเวลา สูง เส้นยิ่งราบรื่น

ตัวอย่างที่ใช้งานได้จริงคือการใช้เส้นแนวโน้มค่าเฉลี่ยเคลื่อนที่เพื่อเปิดเผยความผันผวนของราคาหุ้นที่มิฉะนั้นจะสังเกตได้ยาก

สำหรับข้อมูลเพิ่มเติม โปรดดู: วิธีเพิ่มเส้นแนวโน้มค่าเฉลี่ยเคลื่อนที่ในแผนภูมิ Excel

สมการและสูตรเส้นแนวโน้มของ Excel

ส่วนนี้อธิบายสมการที่ Excel ใช้ สำหรับเส้นแนวโน้มประเภทต่างๆ คุณไม่จำเป็นต้องสร้างสูตรเหล่านี้ด้วยตนเอง เพียงบอกให้ Excel แสดงสมการเส้นแนวโน้มในแผนภูมิ

นอกจากนี้ เราจะหารือเกี่ยวกับสูตรเพื่อหาความชันของเส้นแนวโน้มและค่าสัมประสิทธิ์อื่นๆ สูตรจะถือว่าคุณมีตัวแปร 2 ชุด: ตัวแปรอิสระ x และ ตัวแปรตาม y ในเวิร์กชีตของคุณ คุณสามารถใช้สูตรเหล่านี้เพื่อรับค่า y ที่คาดการณ์ไว้สำหรับค่าใดๆ ที่กำหนดเป็น x

เพื่อความสอดคล้อง เราจะใช้ข้อมูลเดียวกัน กำหนดด้วยค่าที่แตกต่างกันเล็กน้อยสำหรับตัวอย่างทั้งหมด อย่างไรก็ตาม โปรดทราบว่ามันใช้เพื่อการสาธิตเท่านั้น ในเวิร์กชีตจริงของคุณ คุณควรเลือกประเภทเส้นแนวโน้มที่สอดคล้องกับประเภทข้อมูลของคุณ

หมายเหตุสำคัญ! สูตรเส้นแนวโน้มควรใช้กับ แผนภูมิกระจาย XY เท่านั้น เนื่องจากเป็นสูตรนี้เท่านั้นแผนภูมิแปลงทั้งแกน x และ y เป็นค่าตัวเลข สำหรับข้อมูลเพิ่มเติม โปรดดูที่เหตุใดสมการเส้นแนวโน้มของ Excel อาจผิด

สมการเส้นแนวโน้มเชิงเส้นและสูตร

สมการเส้นแนวโน้มเชิงเส้นใช้วิธีกำลังสองน้อยที่สุดเพื่อค้นหา ความชัน และ ค่าสัมประสิทธิ์การสกัดกั้น เช่น:

y = bx + a

โดยที่:

• b คือ ความชัน ของเส้นแนวโน้ม
• a คือ y-intercept ซึ่งเป็นค่าเฉลี่ยที่คาดหวังของ y เมื่อ x<ทั้งหมด 2> ตัวแปรมีค่าเท่ากับ 0 บนแผนภูมิ จุดนี้คือจุดที่เส้นแนวโน้มตัดผ่านแกน y

สำหรับการถดถอยเชิงเส้น Microsoft Excel มีฟังก์ชันพิเศษเพื่อให้ได้ ค่าสัมประสิทธิ์ความชันและจุดตัด

ความชันของเส้นแนวโน้ม

b: =SLOPE(y,x)

จุดตัดแกน Y

a: =INTERCEPT(y,x)

สมมติว่าช่วง x คือ B2:B13 และช่วง y คือ C2:C13 สูตรในชีวิตจริงจะเป็นดังนี้:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

ผลลัพธ์เดียวกันสามารถทำได้โดยใช้ฟังก์ชัน LINEST เป็น สูตรอาร์เรย์ สำหรับสิ่งนี้ ให้เลือก 2 เซลล์ที่อยู่ติดกันในแถวเดียวกัน ป้อนสูตรแล้วกด Ctrl + Shift + Enter เพื่อทำให้เสร็จ:

=LINEST(C2:C13,B2:B13)

ดังที่แสดงในภาพหน้าจอด้านล่าง ความชันและจุดตัด ค่าสัมประสิทธิ์ที่ส่งกลับโดยสูตรนั้นสอดคล้องกับค่าสัมประสิทธิ์ในสมการเส้นแนวโน้มเชิงเส้นที่แสดงในแผนภูมิ เฉพาะค่าหลังเท่านั้นที่ปัดเศษเป็นทศนิยม 4 ตำแหน่ง: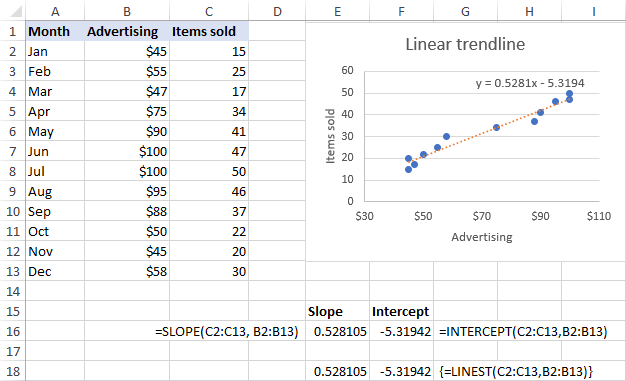

สมการและสูตรเส้นแนวโน้มเลขชี้กำลัง

สำหรับเส้นแนวโน้มเลขชี้กำลัง Excel ใช้สมการต่อไปนี้:

y = aebx

โดยที่ a และ b คือค่าสัมประสิทธิ์ที่คำนวณได้ และ e คือค่าคงที่ทางคณิตศาสตร์ e (ฐานของลอการิทึมธรรมชาติ)

ค่าสัมประสิทธิ์สามารถคำนวณได้โดยใช้สูตรทั่วไปเหล่านี้:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

สำหรับชุดข้อมูลตัวอย่างของเรา สูตรจะมีรูปแบบดังต่อไปนี้:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

สมการเส้นแนวโน้มลอการิทึมและสูตร

นี่คือสมการเส้นแนวโน้มลอการิทึมใน Excel:

y = a*ln(x)+b

โดยที่ a และ b เป็นค่าคงที่ และ ln เป็นฟังก์ชันลอการิทึมธรรมชาติ

หากต้องการรับค่าคงที่ ให้ใช้สูตรทั่วไปเหล่านี้ ซึ่งแตกต่างในอาร์กิวเมนต์สุดท้ายเท่านั้น:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

สำหรับชุดข้อมูลตัวอย่างของเรา เราใช้สิ่งเหล่านี้:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

สมการและสูตรของเส้นแนวโน้มพหุนาม

หากต้องการหาเส้นแนวโน้มพหุนาม Excel จะใช้สมการนี้:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

โดยที่ b ₁ … b ₆ และ a เป็นค่าคงที่

ขึ้นอยู่กับระดับของเส้นแนวโน้มพหุนามของคุณ ใช้หนึ่งในชุดของสูตรต่อไปนี้ เพื่อรับค่าคงที่

เส้นแนวโน้มพหุนามกำลังสอง (ลำดับที่ 2)

สมการ: y = b ₂ x2+ b ₁ x + a<3

ข ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

ข ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

ก: =INDEX(LINEST(y, x^{1,2}), 1, 3)

ลูกบาศก์ (อันดับ 3) เส้นแนวโน้มพหุนาม

สมการ: y = b ₃ x3 + b ₂ x2+ b ₁ x + ก

ข ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

ข ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

ข ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

สูตรสำหรับเส้นแนวโน้มพหุนามระดับสูงกว่าสามารถสร้างได้โดยใช้รูปแบบเดียวกัน

สำหรับชุดข้อมูลของเรา ชุดเส้นแนวโน้มพหุนามลำดับที่ 2 ดีกว่า เราจึงใช้สูตรเหล่านี้:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)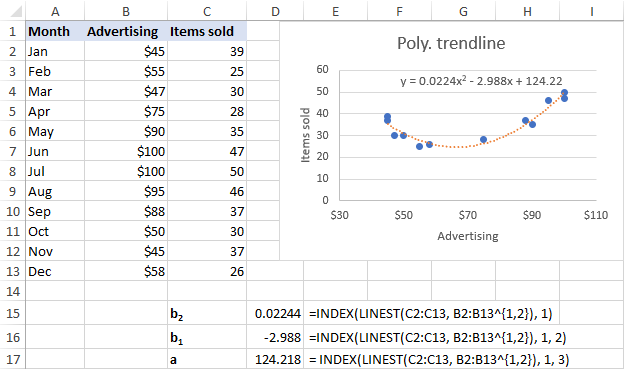

สมการและสูตรของเส้นแนวโน้มยกกำลัง

เส้นแนวโน้มยกกำลังใน Excel วาดตามสมการง่ายๆ นี้:

y = axb

โดยที่ a และ b เป็นค่าคงที่ ซึ่งสามารถคำนวณได้ด้วยสูตรเหล่านี้:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

ในกรณีของเรา สูตรต่อไปนี้ใช้ได้ผล :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

สมการเส้นแนวโน้มของ Excel ไม่ถูกต้อง - เหตุผลและการแก้ไข

หากคุณคิดว่า Excel วาดเส้นแนวโน้มไม่ถูกต้อง หรือสูตรเส้นแนวโน้มที่แสดงในแผนภูมิของคุณไม่ถูกต้อง จุดสองจุดต่อไปนี้อาจทำให้สูญเสียไปบ้าง สถานการณ์ไม่ชัดเจน

สมการเส้นแนวโน้มของ Excel ถูกต้องเฉพาะในแผนภูมิกระจาย

ควรใช้สูตรเส้นแนวโน้มของ Excel กับกราฟ XY (กระจาย) เท่านั้น เนื่องจากในแผนภูมิประเภทนี้มีทั้งแกน y และแกน x จะถูกลงจุดเป็นค่าตัวเลข

ในแผนภูมิเส้น คอลัมน์และกราฟแท่ง ค่าตัวเลขจะถูกลงจุดบนแกน y เท่านั้น แกน x แทนด้วยอนุกรมเชิงเส้น (1, 2,3,…) ไม่ว่าป้ายชื่อแกนจะเป็นตัวเลขหรือข้อความ เมื่อคุณสร้างเส้นแนวโน้มในแผนภูมิเหล่านี้ Excel จะใช้ค่า x สมมติเหล่านั้นในสูตรเส้นแนวโน้ม

ตัวเลขจะถูกปัดเศษในสมการเส้นแนวโน้มของ Excel

หากต้องการใช้พื้นที่น้อยลงในแผนภูมิ Excel จะแสดง มีเลขนัยสำคัญน้อยมากในสมการเส้นแนวโน้ม ดีในแง่ของการออกแบบ มันลดความแม่นยำของสูตรลงอย่างมากเมื่อคุณใส่ค่า x ในสมการด้วยตนเอง

วิธีแก้ปัญหาง่ายๆ คือการแสดงตำแหน่งทศนิยมมากขึ้นในสมการ อีกทางหนึ่ง คุณสามารถคำนวณค่าสัมประสิทธิ์โดยใช้สูตรที่สอดคล้องกับประเภทเส้นแนวโน้มของคุณ และจัดรูปแบบเซลล์สูตรเพื่อให้แสดงทศนิยมในจำนวนที่เพียงพอ สำหรับสิ่งนี้ เพียงคลิกปุ่ม เพิ่มทศนิยม บนแท็บ หน้าแรก ในกลุ่ม จำนวน

นั่นคือวิธีสร้างเส้นแนวโน้มประเภทต่างๆ ใน Excel และรับสมการของพวกเขา ฉันขอขอบคุณที่อ่านและหวังว่าจะได้พบคุณในบล็อกของเราในสัปดาห์หน้า!