বিষয়বস্তুৰ তালিকা
এই টিউটোৰিয়েলত, আপুনি Excel ত উপলব্ধ সকলো ট্ৰেণ্ডলাইন বিকল্পৰ বিশদ বিৱৰণ আৰু কেতিয়া ব্যৱহাৰ কৰিব লাগে। আপুনি এটা চাৰ্টত এটা ট্ৰেণ্ডলাইন সমীকৰণ কেনেকৈ প্ৰদৰ্শন কৰিব লাগে আৰু ট্ৰেণ্ডলাইনৰ ঢাল বিচাৰিব লাগে সেইটোও শিকিব।
এক্সেলত এটা ট্ৰেণ্ডলাইন যোগ কৰাটো অতি সহজ। একমাত্ৰ প্ৰকৃত প্ৰত্যাহ্বানটো হ'ল আপুনি বিশ্লেষণ কৰা তথ্যৰ ধৰণৰ সৈতে সৰ্বোত্তমভাৱে মিল থকা ট্ৰেণ্ডলাইন ধৰণ বাছনি কৰা। এই টিউটোৰিয়েলত আপুনি এক্সেলত উপলব্ধ সকলো ট্ৰেণ্ডলাইন বিকল্প আৰু কেতিয়া ব্যৱহাৰ কৰিব লাগে তাৰ বিশদ বিৱৰণ পাব। যদি আপুনি এক্সেল চাৰ্টত ট্ৰেণ্ডলাইন কেনেকৈ সন্নিবিষ্ট কৰিব বিচাৰিছে, অনুগ্ৰহ কৰি ওপৰত লিংক কৰা টিউটোৰিয়েলটো চাওক।
এক্সেল ট্ৰেণ্ডলাইনৰ ধৰণ
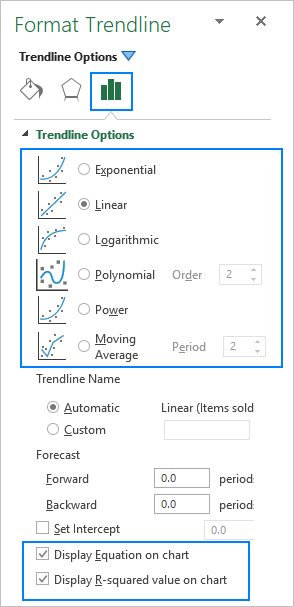
এক্সেলত ট্ৰেণ্ডলাইন যোগ কৰাৰ সময়ত , আপোনাৰ হাতত বাছনি কৰিবলৈ ৬টা ভিন্ন বিকল্প আছে। ইয়াৰ উপৰিও, মাইক্ৰ'ছফ্ট এক্সেলে এটা চাৰ্টত এটা ট্ৰেণ্ডলাইন সমীকৰণ আৰু R-বৰ্গ মান প্ৰদৰ্শন কৰাৰ অনুমতি দিয়ে:
- ট্ৰেণ্ডলাইন সমীকৰণ হৈছে এটা সূত্ৰ যিয়ে তথ্য বিন্দুসমূহৰ সৈতে সৰ্বোত্তমভাৱে মিল থকা এটা ৰেখা বিচাৰি পায়।
- R-বৰ্গ মান য়ে ট্ৰেণ্ডলাইনৰ নিৰ্ভৰযোগ্যতা জুখিব পাৰে - R2 যিমানেই 1 ৰ ওচৰত থাকে, ট্ৰেণ্ডলাইন সিমানেই তথ্যৰ সৈতে ভালদৰে মিলিব।
তলত, আপুনি চাৰ্টৰ উদাহৰণৰ সৈতে প্ৰতিটো ট্ৰেণ্ডলাইন ধৰণৰ চমু বিৱৰণ পাব।
ৰৈখিক ট্ৰেণ্ডলাইন
ৰৈখিক ট্ৰেণ্ডলাইন হোৱাটোৱেই উত্তম ৰৈখিক তথ্যৰ সমষ্টিৰ সৈতে ব্যৱহাৰ কৰা হয় যেতিয়া এটা চাৰ্টৰ তথ্য বিন্দুসমূহ এটা সৰলৰেখাৰ সৈতে মিল খায়। সাধাৰণতে ৰৈখিক ট্ৰেণ্ডলাইনে অবিৰত উত্থান বা পতনৰ বৰ্ণনা কৰেসময়ৰ লগে লগে।
উদাহৰণস্বৰূপে, তলৰ ৰৈখিক ট্ৰেণ্ডলাইনে ৬ মাহৰ ভিতৰত বিক্ৰীৰ ক্ৰমাগত বৃদ্ধি দেখুৱাইছে। আৰু 0.9855 ৰ R2 মানটোৱে আনুমানিক ট্ৰেণ্ডলাইন মানসমূহৰ প্ৰকৃত তথ্যৰ সৈতে যথেষ্ট ভাল ফিট হোৱাৰ ইংগিত দিয়ে। 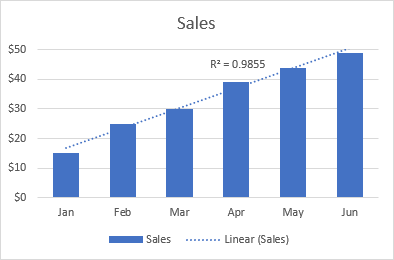
ঘাতীয় ট্ৰেণ্ডলাইন
ঘাতীয় ট্ৰেণ্ডলাইন হৈছে এটা বক্ৰ ৰেখা যিয়ে তথ্যৰ মান বৃদ্ধি বা হ্ৰাস বৃদ্ধি বা হ্ৰাসৰ হাৰত দেখুৱায়, সেয়েহে ৰেখাডাল সাধাৰণতে এটা ফালে অধিক বক্ৰ। এই ট্ৰেণ্ডলাইন ধৰণটো বিজ্ঞানত প্ৰায়ে ব্যৱহাৰ কৰা হয়, উদাহৰণস্বৰূপে বন্যপ্ৰাণীৰ জনসংখ্যাৰ বৃদ্ধি বা হ্ৰাসৰ কল্পনা কৰিবলৈ।
অনুগ্ৰহ কৰি মন কৰক যে শূন্য বা ঋণাত্মক মান থকা তথ্যৰ বাবে এটা ঘাতীয় ট্ৰেণ্ডলাইন সৃষ্টি কৰিব নোৱাৰি।
ঘাতীয় বক্ৰৰ এটা ভাল উদাহৰণ হ’ল পৃথিৱীৰ সমগ্ৰ বন্য বাঘৰ জনসংখ্যাৰ ক্ষয়। 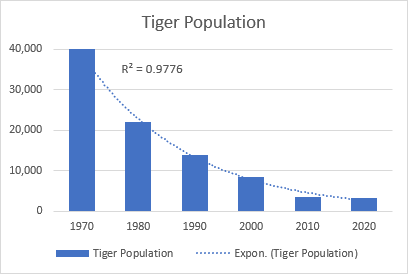
লগাৰিদমিক ট্ৰেণ্ডলাইন
লগাৰিদমিক বেষ্ট-ফিট লাইনক সাধাৰণতে তথ্য প্লট কৰিবলৈ ব্যৱহাৰ কৰা হয় যি দ্ৰুতভাৱে বৃদ্ধি বা হ্ৰাস হয় আৰু তাৰ পিছত লেভেল অফ হয়। ইয়াত ধনাত্মক আৰু ঋণাত্মক দুয়োটা মান অন্তৰ্ভুক্ত হ’ব পাৰে।
লগাৰিদমিক ট্ৰেণ্ডলাইনৰ উদাহৰণ হ’ব পাৰে মুদ্ৰাস্ফীতিৰ হাৰ, যিটো প্ৰথমে বৃদ্ধি পাইছে কিন্তু কিছু সময়ৰ পিছত সুস্থিৰ হৈ পৰিছে। 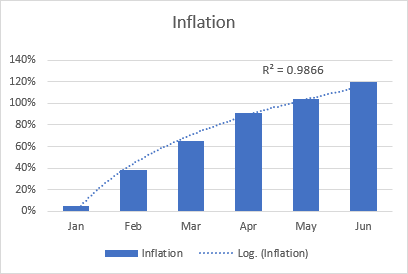
বহুপদ ট্ৰেণ্ডলাইন
বহুপদ বক্ৰৰেখাৰ ট্ৰেণ্ডলাইনে এটাতকৈ অধিক উত্থান আৰু পতন থকা দোলনীয় মান থকা বৃহৎ তথ্যৰ সমষ্টিৰ বাবে ভাল কাম কৰে।
সাধাৰণতে, বহুপদক এই দ্বাৰা শ্ৰেণীভুক্ত কৰা হয় বৃহত্তম ঘাতৰ ডিগ্ৰী। বহুপদ ট্ৰেণ্ডলাইনৰ ডিগ্ৰীয়ে কৰিব পাৰেগ্ৰাফত থকা বেণ্ডৰ সংখ্যাৰ দ্বাৰাও নিৰ্ণয় কৰা হ’ব। সাধাৰণতে, এটা দ্বিঘাত বহুপদ ট্ৰেণ্ডলাইনৰ এটা বেণ্ড (পাহাৰ বা উপত্যকা), এটা ঘন বহুপদত ১ বা ২ টা বেণ্ড থাকে, আৰু এটা চতুৰ্থাংশ বহুপদৰ ৩ টালৈকে বেণ্ড থাকে।
এটা এক্সেল চাৰ্টত এটা বহুপদ ট্ৰেণ্ডলাইন যোগ কৰাৰ সময়ত, আপুনি ডিগ্ৰী ধাৰ্য্য কৰে ফৰ্মেট ট্ৰেণ্ডলাইন পেনত ক্ৰম বাকচত সংশ্লিষ্ট সংখ্যা টাইপ কৰি, যি অবিকল্পিতভাৱে 2: 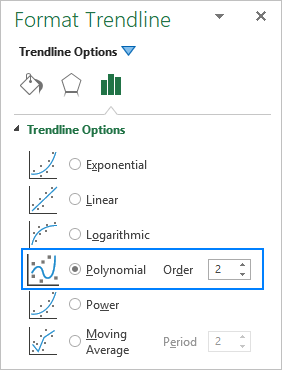
উদাহৰণস্বৰূপে, দ্বিঘাত বহুপদ ট্ৰেণ্ড তলৰ গ্ৰাফটোত স্পষ্ট হৈ পৰে যিয়ে লাভ আৰু পণ্যটো বজাৰত থকা বছৰৰ সংখ্যাৰ মাজৰ সম্পৰ্ক দেখুৱাইছে: আৰম্ভণিতে বৃদ্ধি, মাজত শিখৰ আৰু শেষৰ ওচৰত পতন। 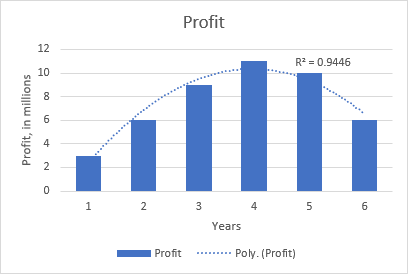
শক্তিৰ ধাৰাৰেখা
শক্তিৰ ধাৰা ৰেখা ঘাত বক্ৰৰ সৈতে বহুত মিল আছে, কেৱল ইয়াৰ অধিক প্ৰতিসম চাপ থাকে। ইয়াক সাধাৰণতে এটা নিৰ্দিষ্ট হাৰত বৃদ্ধি পোৱা জোখ-মাখ প্লট কৰিবলৈ ব্যৱহাৰ কৰা হয়।
শূন্য বা ঋণাত্মক মান থকা এক্সেল চাৰ্টত এটা শক্তি ট্ৰেণ্ডলাইন যোগ কৰিব নোৱাৰি।
উদাহৰণ হিচাপে, a আঁকক ৰাসায়নিক বিক্ৰিয়াৰ হাৰ কল্পনা কৰিবলৈ শক্তিৰ ট্ৰেণ্ডলাইন। মন কৰক R-squared মান 0.9918, অৰ্থাৎ আমাৰ ট্ৰেণ্ডলাইনে তথ্যৰ সৈতে প্ৰায় নিখুঁতভাৱে মিলি যায়। 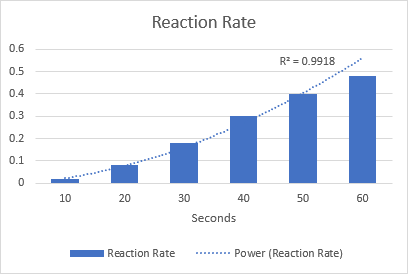
মুভিং এভাৰেজ ট্ৰেণ্ডলাইন
যেতিয়া আপোনাৰ চাৰ্টৰ ডাটা পইণ্টসমূহত বহুত উত্থান-পতন থাকে, এটা মুভিং এভাৰেজ ট্ৰেণ্ডলাইনে ডাটা মানসমূহৰ চৰম উঠা-নমাক মসৃণ কৰিব পাৰে যাতে এটা আৰ্হি অধিক স্পষ্টভাৱে দেখুৱাব পাৰে। ইয়াৰ বাবে এক্সেলে গণনা কৰেআপুনি ধাৰ্য্য কৰা সময়ৰ সংখ্যাৰ চলন্ত গড় (2 অবিকল্পিতভাৱে) আৰু সেই গড় মানসমূহক শাৰীত বিন্দু হিচাপে ৰাখে। পিৰিয়ড মান যিমানেই বেছি হ'ব সিমানেই ৰেখাডাল মসৃণ হ'ব।
এটা ভাল ব্যৱহাৰিক উদাহৰণ হ'ল ষ্টকৰ মূল্যৰ উঠা-নমা উন্মোচন কৰিবলৈ চলন্ত গড় ট্ৰেণ্ডলাইন ব্যৱহাৰ কৰা যিটো অন্যথা পৰ্যবেক্ষণ কৰাটো কঠিন হ'ব। 
অধিক তথ্যৰ বাবে, অনুগ্ৰহ কৰি চাওক: এটা এক্সেল চাৰ্টত এটা চলন্ত গড় ট্ৰেণ্ডলাইন কেনেকৈ যোগ কৰিব পাৰি।
এক্সেল ট্ৰেণ্ডলাইন সমীকৰণ আৰু সূত্ৰসমূহ
এই অংশত এক্সেলে ব্যৱহাৰ কৰা সমীকৰণসমূহৰ বিষয়ে বৰ্ণনা কৰা হৈছে বিভিন্ন ট্ৰেণ্ডলাইন ধৰণৰ বাবে। আপুনি এই সূত্ৰসমূহ নিজেই নিৰ্মাণ কৰিব নালাগে, কেৱল এক্সেলক ট্ৰেণ্ডলাইন সমীকৰণটো এটা চাৰ্টত প্ৰদৰ্শন কৰিবলৈ কওক।
আৰু, আমি এটা ট্ৰেণ্ডলাইনৰ ঢাল আৰু অন্যান্য সহগসমূহ বিচাৰি উলিয়াবলৈ সূত্ৰটোৰ বিষয়ে আলোচনা কৰিম। সূত্ৰসমূহে ধৰি লৈছে যে আপোনাৰ ২টা চলকসমূহৰ গোট আছে: স্বাধীন চলক x আৰু নিৰ্ভৰশীল চলক y । আপোনাৰ কাৰ্য্যপত্ৰিকাসমূহত, আপুনি এই সূত্ৰসমূহ ব্যৱহাৰ কৰিব পাৰে x ৰ যিকোনো প্ৰদত্ত মানসমূহৰ বাবে ভৱিষ্যদ্বাণী কৰা y মানসমূহ পাবলৈ।
সামঞ্জস্যতাৰ বাবে, আমি একে তথ্য ব্যৱহাৰ কৰিম সকলো উদাহৰণৰ বাবে সামান্য ভিন্ন মানসমূহৰ সৈতে সংহতি কৰক। অৱশ্যে মনত ৰাখিব যে ই কেৱল প্ৰদৰ্শনৰ উদ্দেশ্যেহে। আপোনাৰ প্ৰকৃত কাৰ্য্যপত্ৰিকাসমূহত, আপুনি আপোনাৰ তথ্যৰ ধৰণৰ সৈতে সংগতি ৰাখি ট্ৰেণ্ডলাইন ধৰণ নিৰ্ব্বাচন কৰিব লাগে।
গুৰুত্বপূৰ্ণ টোকা! ট্ৰেণ্ডলাইন সূত্ৰসমূহ কেৱল XY স্কেটাৰ চাৰ্ট ৰ সৈতে ব্যৱহাৰ কৰিব লাগে কাৰণ কেৱল এইটোৱেইচাৰ্টে x আৰু y দুয়োটা অক্ষক সংখ্যাগত মান হিচাপে প্লট কৰে। অধিক তথ্যৰ বাবে, অনুগ্ৰহ কৰি চাওক কিয় এক্সেল ট্ৰেণ্ডলাইন সমীকৰণ ভুল হ'ব পাৰে।
ৰৈখিক ট্ৰেণ্ডলাইন সমীকৰণ আৰু সূত্ৰসমূহ
ৰৈখিক ট্ৰেণ্ডলাইন সমীকৰণে ঢাল বিচাৰিবলৈ নূন্যতম বৰ্গ পদ্ধতি ব্যৱহাৰ কৰে আৰু আটক সহগসমূহ এনেদৰে যে:
y = bx + aয'ত:
- b হৈছে ঢাল
- a হৈছে y-intercept , যিটো হৈছে y ৰ প্ৰত্যাশিত গড় মান যেতিয়া সকলো x চলকসমূহ 0 ৰ সমান। এটা চাৰ্টত, ই সেই বিন্দু য'ত ট্ৰেণ্ডলাইনে y অক্ষ অতিক্ৰম কৰে।
ৰৈখিক ৰিগ্ৰেছনৰ বাবে, মাইক্ৰ'ছফ্ট এক্সেলে লাভ কৰিবলৈ বিশেষ ফাংচন প্ৰদান কৰে ঢাল আৰু ইন্টাৰচেপ্ট সহগ।
ট্ৰেণ্ডলাইনৰ ঢাল
b: =SLOPE(y,x)
Y-ইণ্টাৰচেপ্ট
a: =INTERCEPT(y,x)
x পৰিসীমা B2:B13 আৰু y পৰিসীমা C2:C13 বুলি ধৰি ল'লে, বাস্তৱ জীৱনৰ সূত্ৰসমূহ তলত দিয়া ধৰণে যায়:
=SLOPE(C2:C13, B2:B13)
=INTERCEPT(C2:C13,B2:B13)
LINEST ফাংচনক এৰে সূত্ৰ হিচাপে ব্যৱহাৰ কৰি একে ফলাফল লাভ কৰিব পাৰি। ইয়াৰ বাবে, একে শাৰীত ২টা কাষৰ ঘৰ নিৰ্ব্বাচন কৰক, সূত্ৰটো সুমুৱাওক আৰু ইয়াক সম্পূৰ্ণ কৰিবলৈ Ctrl + Shift + Enter টিপক:
=LINEST(C2:C13,B2:B13)
তলৰ স্ক্ৰীণশ্বটত দেখুওৱাৰ দৰে, ঢাল আৰু ইন্টাৰচেপ্ট সূত্ৰসমূহে ঘূৰাই দিয়া সহগসমূহ চাৰ্টত প্ৰদৰ্শিত ৰৈখিক ট্ৰেণ্ডলাইন সমীকৰণৰ সহগসমূহৰ সৈতে নিখুঁতভাৱে মিল থাকে, কেৱল পিছৰবোৰক ৪টা দশমিক স্থানলৈ ঘূৰণীয়া কৰা হয়: 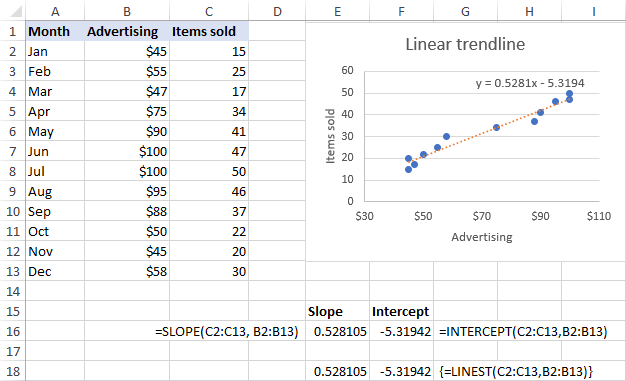
ঘাতীয় ট্ৰেণ্ডলাইন সমীকৰণ আৰু সূত্ৰ
ঘাতীয় ট্ৰেণ্ডলাইনৰ বাবে এক্সেলে তলত দিয়া সমীকৰণটো ব্যৱহাৰ কৰে:
y = aebxয'ত a আৰু b গণনা কৰা সহগ আৰু e হৈছে গাণিতিক ধ্ৰুৱক e (প্ৰাকৃতিক লগাৰিদমৰ ভিত্তি)।
এই সাধাৰণ সূত্ৰসমূহ ব্যৱহাৰ কৰি সহগসমূহ গণনা কৰিব পাৰি:
a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))
b: =INDEX(LINEST(LN(y), x), 1)
আমাৰ নমুনা তথ্যৰ গোটৰ বাবে সূত্ৰসমূহে তলত দিয়া আকৃতি লয়:
a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))
b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1) 
লগাৰিদমিক ট্ৰেণ্ডলাইন সমীকৰণ আৰু সূত্ৰসমূহ
ইয়াত এক্সেলত লগাৰিদমিক ট্ৰেণ্ডলাইন সমীকৰণটো আছে:
y = a*ln(x)+bয'ত a আৰু b ধ্ৰুৱক আৰু ln হৈছে প্ৰাকৃতিক লগাৰিদম ফলন।
ধ্ৰুৱকসমূহ পাবলৈ, এই সাধাৰণ সূত্ৰসমূহ ব্যৱহাৰ কৰক, যিবোৰ কেৱল শেষৰ যুক্তিত পৃথক:
a: =INDEX(LINEST(y, LN(x)), 1)
b: =INDEX(LINEST(y, LN(x)), 1, 2)
আমাৰ নমুনা ডাটা ছেটৰ বাবে আমি এইবোৰ ব্যৱহাৰ কৰো:
a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)
b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2) 
বহুপদ ট্ৰেণ্ডলাইন সমীকৰণ আৰু সূত্ৰ
বহুপদ ট্ৰেণ্ডলাইন কাম কৰিবলৈ এক্সেলে এই সমীকৰণটো ব্যৱহাৰ কৰে:
y = b 6 x6 + ... + b 2 x2 + b 1 x + aয'ত b 1 ... b 6 আৰু a ধ্ৰুৱক।
আপোনাৰ বহুপদ ট্ৰেণ্ডলাইনৰ ডিগ্ৰীৰ ওপৰত নিৰ্ভৰ কৰি, নিম্নলিখিত সূত্ৰৰ এটা গোট ব্যৱহাৰ কৰক ধ্ৰুৱকসমূহ পাবলৈ।
দ্বিঘাত (দ্বিতীয় ক্ৰমৰ) বহুপদ ট্ৰেণ্ডলাইন
সমীকৰণ: y = b 2 x2+ b 1 x + a
b 2 : =INDEX(LINEST(y, x^{1,2}), 1)
b 1 : =INDEX(LINEST(y, x^{1,2}), 1, 2)
ক:৯১৯২
ঘন (তৃতীয় ক্ৰমৰ) বহুপদ ধাৰাৰেখা
সমীকৰণ: y = b 3 x3 + b 2 x2+ b 1 x + a
b 3 : =INDEX(LINEST(y, x^{1,2,3}), 1)
b 2 : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)
b 1 : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)
a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)
উচ্চ ডিগ্ৰী বহুপদ ট্ৰেণ্ডলাইনৰ বাবে সূত্ৰসমূহ একেটা আৰ্হি ব্যৱহাৰ কৰি নিৰ্মাণ কৰিব পাৰি।
আমাৰ ডাটা ছেটৰ বাবে, ২য় ক্ৰমৰ বহুপদ ট্ৰেণ্ডলাইন চুইট ভাল, গতিকে আমি এই সূত্ৰবোৰ ব্যৱহাৰ কৰিছো:
b 2 : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)
b 1 : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)
a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3) 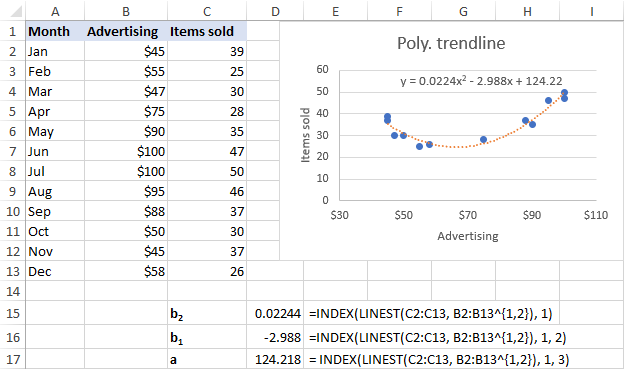
শক্তিৰ ট্ৰেণ্ডলাইন সমীকৰণ আৰু সূত্ৰসমূহ
এই সৰল সমীকৰণৰ ওপৰত ভিত্তি কৰি এক্সেলত এটা শক্তি ট্ৰেণ্ডলাইন অংকন কৰা হয়:
y = axbয'ত a আৰু b ধ্ৰুৱক, যিবোৰ এই সূত্ৰবোৰৰ সহায়ত গণনা কৰিব পাৰি:
a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))
b: =INDEX(LINEST(LN(y), LN(x),,), 1)
আমাৰ ক্ষেত্ৰত তলত দিয়া সূত্ৰবোৰে এটা ট্ৰিট কাম কৰে :
a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))
b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1) 
এক্সেল ট্ৰেণ্ডলাইন সমীকৰণ ভুল - কাৰণ আৰু সমাধান
যদি আপুনি ভাৱে যে এক্সেলে ভুলকৈ ট্ৰেণ্ডলাইন অংকন কৰিছে বা আপোনাৰ চাৰ্টত প্ৰদৰ্শিত ট্ৰেণ্ডলাইন সূত্ৰ ভুল, নিম্নলিখিত দুটা পইণ্টে কিছুমান শ্বেড কৰিব পাৰে
এক্সেল ট্ৰেণ্ডলাইন সমীকৰণ কেৱল স্কেটাৰ চাৰ্টত শুদ্ধ
এক্সেল ট্ৰেণ্ডলাইন সূত্ৰ কেৱল XY (স্কেটাৰ) গ্ৰাফৰ সৈতেহে ব্যৱহাৰ কৰিব লাগে কাৰণ কেৱল এই চাৰ্টতহে y-অক্ষ দুয়োটা টাইপ কৰিব লাগে আৰু x-অক্ষক সংখ্যাগত মান হিচাপে প্লট কৰা হয়।
লাইন চাৰ্ট, স্তম্ভ আৰু বাৰ গ্ৰাফত, সংখ্যাগত মানসমূহ কেৱল y-অক্ষত প্লট কৰা হয়। x-অক্ষক এটা ৰৈখিক শৃংখলা (1, 2, 2) দ্বাৰা প্ৰতিনিধিত্ব কৰা হয়।৩,...) অক্ষৰ লেবেলবোৰ সংখ্যা বা লিখনী হওক বা নহওক। যেতিয়া আপুনি এই চাৰ্টসমূহত এটা ট্ৰেণ্ডলাইন বনায়, এক্সেলে ট্ৰেণ্ডলাইন সূত্ৰত সেই ধাৰণা কৰা x-মানসমূহ ব্যৱহাৰ কৰে।
সংখ্যাসমূহক এক্সেল ট্ৰেণ্ডলাইন সমীকৰণত ঘূৰণীয়া কৰা হয়
চাৰ্টত কম স্থান দখল কৰিবলৈ, এক্সেলে প্ৰদৰ্শন কৰে ট্ৰেণ্ডলাইন সমীকৰণত অতি কম উল্লেখযোগ্য সংখ্যা। ডিজাইনৰ ক্ষেত্ৰত ভাল, ই সূত্ৰৰ সঠিকতা বহু পৰিমাণে হ্ৰাস কৰে যেতিয়া আপুনি সমীকৰণত x মানসমূহ হস্তচালিতভাৱে যোগান ধৰে।
এটা সহজ সমাধান হ'ল সমীকৰণটোত অধিক দশমিক স্থান দেখুওৱা। বিকল্পভাৱে, আপুনি আপোনাৰ ট্ৰেণ্ডলাইন ধৰণৰ সৈতে সংগতি ৰাখি এটা সূত্ৰ ব্যৱহাৰ কৰি সহগসমূহ গণনা কৰিব পাৰে, আৰু সূত্ৰ কোষসমূহ ফৰ্মেট কৰিব পাৰে যাতে সিহঁতে পৰ্যাপ্ত সংখ্যক দশমিক স্থান দেখুৱায়। ইয়াৰ বাবে, কেৱল সংখ্যা গোটত ঘৰ টেবত দশমিক বৃদ্ধি বুটাম ক্লিক কৰক।
তেনেকৈয়ে আপুনি বিভিন্ন ট্ৰেণ্ডলাইন ধৰণ বনাব পাৰে এক্সেলত যোগ কৰক আৰু তেওঁলোকৰ সমীকৰণসমূহ লাভ কৰক। পঢ়াৰ বাবে ধন্যবাদ আৰু অহা সপ্তাহত আমাৰ ব্লগত লগ পাম বুলি আশা কৰিলোঁ!
<৩><৩>
