In questa esercitazione troverete una descrizione dettagliata di tutte le opzioni di trendline disponibili in Excel e di quando utilizzarle. Imparerete anche a visualizzare l'equazione di una trendline in un grafico e a trovare la pendenza della trendline.

È molto facile aggiungere una linea di tendenza in Excel. L'unica vera sfida è scegliere il tipo di linea di tendenza che meglio corrisponde al tipo di dati che si sta analizzando. In questo tutorial, troverete la descrizione dettagliata di tutte le opzioni di linea di tendenza disponibili in Excel e quando utilizzarle. Se state cercando come inserire una linea di tendenza in un grafico di Excel, consultate il tutorial collegato sopra.

Tipi di linee di tendenza di Excel

Quando si aggiunge una linea di tendenza in Excel, si possono scegliere 6 diverse opzioni. Inoltre, Microsoft Excel consente di visualizzare l'equazione della linea di tendenza e il valore R-squared in un grafico:

• Equazione della linea di tendenza è una formula che individua la retta che meglio si adatta ai punti dei dati.
• Valore R-quadro misura l'affidabilità della linea di tendenza: quanto più R2 è vicino a 1, tanto meglio la linea di tendenza si adatta ai dati.

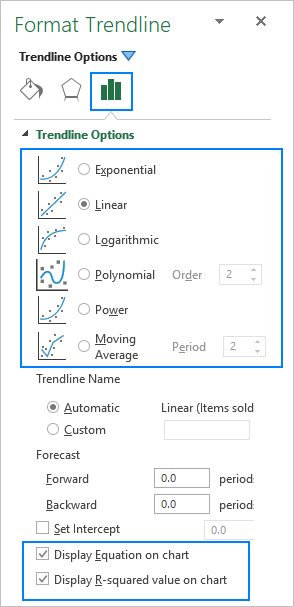
Di seguito troverete una breve descrizione di ciascun tipo di trendline con esempi di grafici.

Linea di tendenza lineare

La linea di tendenza lineare si utilizza al meglio con le serie di dati lineari quando i punti dei dati in un grafico assomigliano a una linea retta. In genere, una linea di tendenza lineare descrive un aumento o una diminuzione continua nel tempo.

Ad esempio, la seguente linea di tendenza lineare mostra un aumento costante delle vendite nell'arco di 6 mesi e il valore R2 di 0,9855 indica un buon adattamento dei valori stimati della linea di tendenza ai dati reali.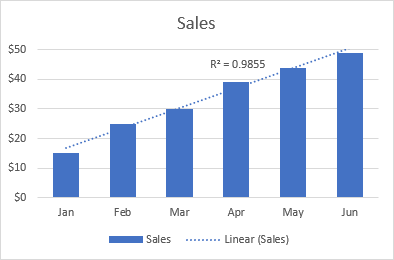

Linea di tendenza esponenziale

La linea di tendenza esponenziale è una linea curva che illustra l'aumento o la diminuzione dei valori dei dati a un ritmo crescente, quindi la linea è solitamente più curva su un lato. Questo tipo di linea di tendenza è spesso utilizzato nelle scienze, ad esempio per visualizzare la crescita della popolazione umana o il declino delle popolazioni di animali selvatici.

Si noti che non è possibile creare una linea di tendenza esponenziale per i dati che contengono zeri o valori negativi.

Un buon esempio di curva esponenziale è il declino dell'intera popolazione di tigri selvatiche sulla terra.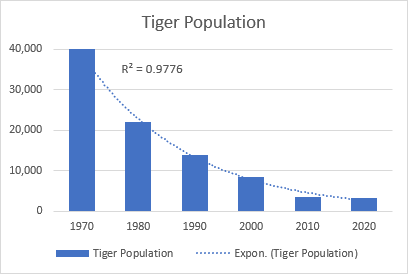

Linea di tendenza logaritmica

La linea logaritmica di miglior adattamento viene generalmente utilizzata per tracciare dati che aumentano o diminuiscono rapidamente e poi si stabilizzano. Può includere sia valori positivi che negativi.

Un esempio di linea di tendenza logaritmica può essere il tasso di inflazione, che all'inizio aumenta ma dopo un po' si stabilizza.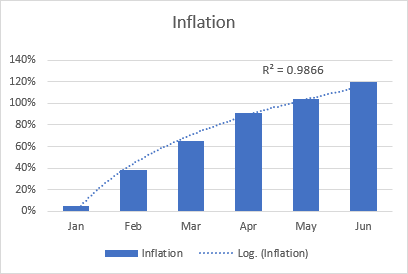

Linea di tendenza polinomiale

La linea di tendenza polinomiale curvilinea funziona bene per grandi insiemi di dati con valori oscillanti che presentano più di un aumento e una diminuzione.

In generale, un polinomio viene classificato in base al grado dell'esponente maggiore. Il grado della linea di tendenza polinomiale può essere determinato anche dal numero di curve presenti nel grafico. In genere, una linea di tendenza polinomiale quadratica presenta una sola curva (collina o valle), una polinomiale cubica ha 1 o 2 curve e una polinomiale quartica ha fino a 3 curve.

Quando si aggiunge una linea di tendenza polinomiale in un grafico di Excel, si specifica il grado digitando il numero corrispondente nel campo Ordine sulla casella Formato Linea di tendenza che per impostazione predefinita è 2: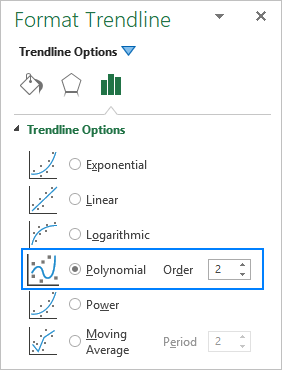

Ad esempio, l'andamento polinomiale quadratico è evidente nel seguente grafico che mostra la relazione tra il profitto e il numero di anni di presenza del prodotto sul mercato: aumento all'inizio, picco a metà e calo verso la fine.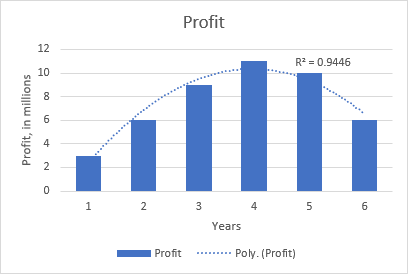

Linea di tendenza della potenza

La linea di tendenza della potenza è molto simile alla curva esponenziale, solo che ha un arco più simmetrico. Viene comunemente utilizzata per tracciare misure che aumentano a una certa velocità.

Non è possibile aggiungere una power trendline a un grafico Excel che contiene valori zero o negativi.

A titolo di esempio, tracciamo una linea di tendenza di potenza per visualizzare il tasso di reazione chimica. Si noti il valore R-squared di 0,9918, che significa che la nostra linea di tendenza si adatta quasi perfettamente ai dati.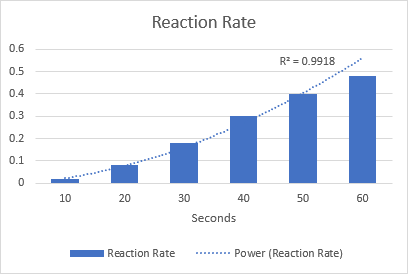

Linea di tendenza della media mobile

Quando i punti dei dati nel grafico presentano molti alti e bassi, una linea di tendenza a media mobile può attenuare le fluttuazioni estreme dei valori dei dati per mostrare più chiaramente un modello. A tal fine, Excel calcola la media mobile del numero di periodi specificato (2 per impostazione predefinita) e inserisce questi valori medi come punti nella linea. Più alto è il valore della media mobile, più alto è il valore della media mobile. Periodo più il valore è alto, più la linea è liscia.

Un buon esempio pratico è l'utilizzo della linea di tendenza della media mobile per rivelare le fluttuazioni del prezzo di un'azione che altrimenti sarebbero difficili da osservare.

Per ulteriori informazioni, consultare: Come aggiungere una linea di tendenza della media mobile a un grafico Excel.

Equazioni e formule per le linee di tendenza in Excel

Questa sezione descrive le equazioni utilizzate da Excel per i diversi tipi di linee di tendenza. Non è necessario costruire queste formule manualmente, ma è sufficiente indicare a Excel di visualizzare l'equazione della linea di tendenza in un grafico.

Inoltre, discuteremo la formula per trovare la pendenza di una linea di tendenza e altri coefficienti. Le formule presuppongono l'esistenza di due serie di variabili: variabile indipendente x e variabile dipendente y Nei fogli di lavoro, è possibile utilizzare queste formule per ottenere le previsioni. y per qualsiasi valore di x .

Per coerenza, utilizzeremo lo stesso set di dati con valori leggermente diversi per tutti gli esempi. Tuttavia, tenete presente che è solo a scopo dimostrativo. Nei vostri fogli di lavoro reali, dovrete scegliere il tipo di linea di tendenza corrispondente al vostro tipo di dati.

Nota importante: le formule delle linee di tendenza devono essere utilizzate solo con Grafici a dispersione XY perché solo questo grafico traccia entrambi x e y Per ulteriori informazioni, vedere Perché l'equazione delle linee di tendenza di Excel potrebbe essere sbagliata.

Equazione e formule della linea di tendenza lineare

L'equazione della linea di tendenza lineare utilizza i metodi dei minimi quadrati per ricercare il valore di pendenza e intercettazione coefficienti tali che:

Dove:

• b è il pendenza di una linea di tendenza.
• a è il Intercetta y , che è il valore medio atteso di y quando tutti x sono uguali a 0. Su un grafico, è il punto in cui la linea di tendenza incrocia la linea di tendenza. y asse.

Per la regressione lineare, Microsoft Excel fornisce funzioni speciali per ottenere i coefficienti di pendenza e di intercetta.

Pendenza della linea di tendenza

b: =SLOPE(y,x)

Intercetta Y

a: =INTERCETTA(y,x)

Supponendo che il x è B2:B13 e l'intervallo y L'intervallo è C2:C13, le formule reali sono le seguenti:

=PENDENZA(C2:C13, B2:B13)

=INTERCETTA(C2:C13,B2:B13)

Gli stessi risultati possono essere ottenuti utilizzando la funzione LINEST come un'applicazione formula dell'array Per questo, selezionare 2 celle adiacenti nella stessa riga, inserire la formula e premere Ctrl + Maiusc + Invio per completarla:

=LINEST(C2:C13,B2:B13)

Come mostrato nella schermata sottostante, i coefficienti di pendenza e intercetta restituiti dalle formule sono perfettamente in linea con i coefficienti dell'equazione della linea di tendenza lineare visualizzata nel grafico, solo che questi ultimi sono arrotondati a 4 cifre decimali: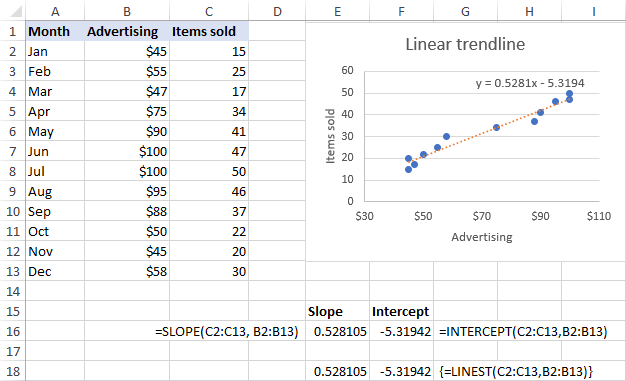

Equazione e formule della linea di tendenza esponenziale

Per la linea di tendenza esponenziale, Excel utilizza la seguente equazione:

Dove a e b sono i coefficienti calcolati ed e è la costante matematica e (la base del logaritmo naturale).

I coefficienti possono essere calcolati utilizzando queste formule generiche:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Per il nostro set di dati campione, le formule assumono la forma seguente:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDICE(LINEST(LN(C2:C13), B2:B13), 1)

Equazione e formule della linea di tendenza logaritmica

Ecco l'equazione della linea di tendenza logaritmica in Excel:

Dove a e b sono costanti e ln è la funzione del logaritmo naturale.

Per ottenere le costanti, utilizzare queste formule generiche, che differiscono solo per l'ultimo argomento:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Per il nostro set di dati campione, utilizziamo questi:

a: =INDICE(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDICE(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Equazione e formule della linea di tendenza polinomiale

Per elaborare la linea di tendenza polinomiale, Excel utilizza questa equazione:

Dove b ₁ ... b ₆ e a sono costanti.

A seconda del grado della linea di tendenza polinomiale, utilizzare una delle seguenti serie di formule per ottenere le costanti.

Linea di tendenza polinomiale quadratica (2° ordine)

Equazione: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Linea di tendenza polinomiale cubica (3° ordine)

Equazione: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Le formule per le linee di tendenza polinomiali di grado superiore possono essere costruite utilizzando lo stesso schema.

Per il nostro set di dati, la linea di tendenza polinomiale del 2° ordine si adatta meglio, quindi utilizziamo queste formule:

b ₂ : =INDICE(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDICE(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDICE(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)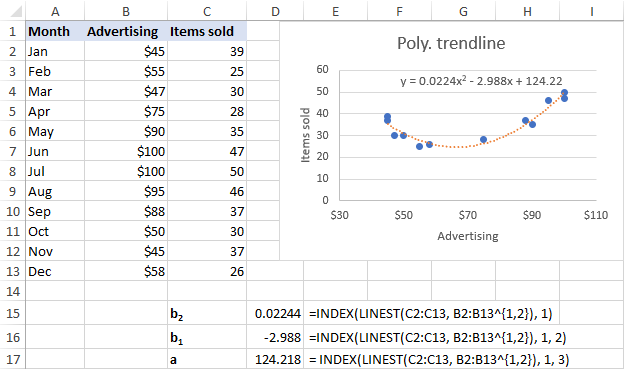

Equazione e formule della linea di tendenza di potenza

Una power trendline in Excel viene tracciata sulla base di questa semplice equazione:

Dove a e b sono costanti che possono essere calcolate con queste formule:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),), 1)

Nel nostro caso, le seguenti formule funzionano a meraviglia:

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDICE(LINEST(LN(C2:C13), LN(B2:B13),), 1)

L'equazione della linea di tendenza di Excel è sbagliata: motivi e soluzioni

Se pensate che Excel abbia disegnato una linea di tendenza in modo errato o che la formula della linea di tendenza visualizzata nel grafico sia sbagliata, i due punti seguenti possono chiarire la situazione.

L'equazione della linea di tendenza di Excel è corretta solo nei grafici a dispersione

Le formule per le linee di tendenza di Excel devono essere utilizzate solo con i grafici XY (a dispersione) perché solo in questo tipo di grafico sia l'asse y che l'asse x sono tracciati come valori numerici.

Nei grafici a linee, a colonne e a barre, i valori numerici sono tracciati solo sull'asse delle ordinate. L'asse delle ascisse è rappresentato da una serie lineare (1, 2, 3,...) indipendentemente dal fatto che le etichette dell'asse siano numeri o testo. Quando si crea una linea di tendenza in questi grafici, Excel utilizza i valori delle ascisse presunti nella formula della linea di tendenza.

I numeri sono arrotondati nell'equazione delle linee di tendenza di Excel.

Per occupare meno spazio nel grafico, Excel visualizza un numero molto ridotto di cifre significative in un'equazione della linea di tendenza. Sebbene sia piacevole in termini di design, riduce significativamente l'accuratezza della formula quando si forniscono manualmente i valori di x nell'equazione.

In alternativa, è possibile calcolare i coefficienti utilizzando una formula corrispondente al tipo di linea di tendenza e formattando le celle della formula in modo che mostrino un numero sufficiente di cifre decimali. A tal fine, è sufficiente fare clic sul tasto Aumenta Decimale sul pulsante Casa nella scheda Numero gruppo.

Ecco come è possibile creare diversi tipi di linee di tendenza in Excel e ottenere le relative equazioni. Vi ringrazio per la lettura e spero di vedervi sul nostro blog la prossima settimana!