I denne vejledning finder du en detaljeret beskrivelse af alle de trendlinjemuligheder, der er tilgængelige i Excel, og hvornår de skal bruges. Du lærer også, hvordan du viser en trendlinjeligning i et diagram og finder trendlinjens hældning.

Det er meget nemt at tilføje en trendlinje i Excel. Den eneste virkelige udfordring er at vælge den trendlinjetype, der bedst svarer til den type data, du analyserer. I denne vejledning finder du en detaljeret beskrivelse af alle de trendlinjemuligheder, der er tilgængelige i Excel, og hvornår du skal bruge dem. Hvis du leder efter, hvordan du indsætter en trendlinje i et Excel-diagram, kan du tjekke den ovenfor linkede vejledning.

Excel trendlinjetyper

Når du tilføjer en trendlinje i Excel, har du 6 forskellige muligheder at vælge imellem. Microsoft Excel gør det desuden muligt at vise en trendlinjeligning og R-kvadrat-værdi i et diagram:

• Ligning for tendenslinje er en formel, der finder en linje, der passer bedst til datapunkterne.
• R-kvadrat-værdi måler trendlinjens pålidelighed - jo tættere R2 er på 1, jo bedre passer trendlinjen til dataene.

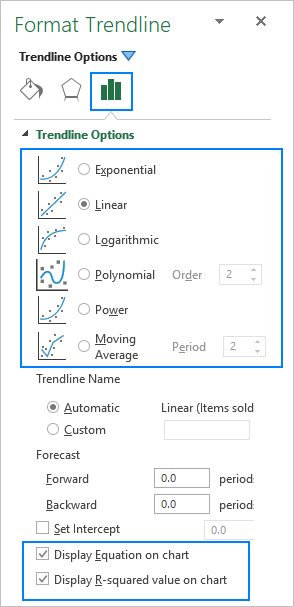
Nedenfor finder du en kort beskrivelse af hver enkelt trendlinjetype med diagrameksempler.

Lineær tendenslinje

Den lineære trendlinje er bedst egnet til brug med lineære datasæt, når datapunkterne i et diagram ligner en lige linje. En lineær trendlinje beskriver typisk en kontinuerlig stigning eller et kontinuerligt fald over tid.

Den følgende lineære trendlinje viser f.eks. en konstant stigning i salget i løbet af 6 måneder, og R2-værdien på 0,9855 viser en ret god overensstemmelse mellem de estimerede trendlinjerværdier og de faktiske data.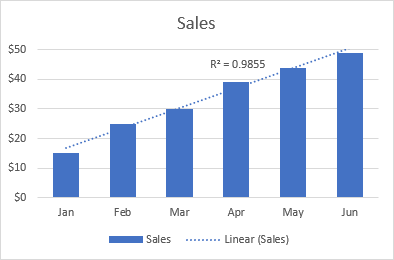

Eksponentiel trendlinje

Den eksponentielle trendlinje er en buet linje, der illustrerer en stigning eller et fald i dataværdierne med stigende hastighed, og derfor er linjen normalt mere buet på den ene side. Denne trendlinjetype bruges ofte inden for videnskaben, f.eks. til at visualisere en menneskelig befolkningstilvækst eller et fald i vildtbestande.

Bemærk, at der ikke kan oprettes en eksponentiel trendlinje for data, der indeholder nuller eller negative værdier.

Et godt eksempel på en eksponentiel kurve er nedgangen i hele den vilde tigerbestand på jorden.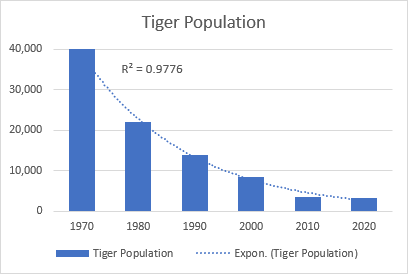

Logaritmisk trendlinje

Den logaritmiske linje med den bedste tilpasning bruges generelt til at plotte data, der hurtigt stiger eller falder og derefter falder i niveau. Den kan indeholde både positive og negative værdier.

Et eksempel på en logaritmisk trendlinje kan være en inflationstakt, som først stiger, men som efter et stykke tid stabiliserer sig.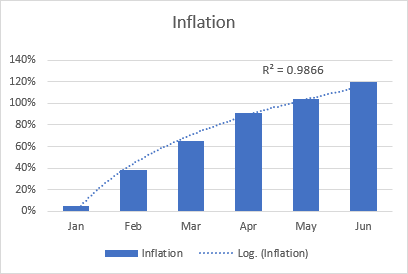

Polynomial trendlinje

Den polynomiale kurvilineære trendlinje fungerer godt til store datasæt med svingende værdier, der har mere end én stigning og ét fald.

Generelt klassificeres et polynomium efter graden af den største eksponent. Graden af den polynomiske trendlinje kan også bestemmes ud fra antallet af bøjninger på en graf. Typisk har en kvadratisk polynomisk trendlinje én bøjning (bakke eller dal), et kubisk polynomium har 1 eller 2 bøjninger, og et kvartisk polynomium har op til 3 bøjninger.

Når du tilføjer en polynomial trendlinje i et Excel-diagram, skal du angive graden ved at skrive det tilsvarende tal i feltet Bestil feltet på den Format Trendline rude, som som er 2 som standard: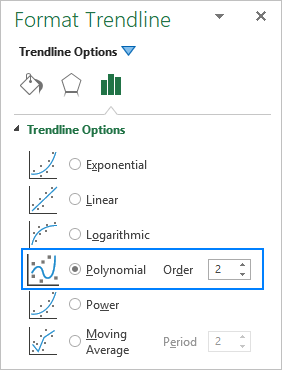

Den kvadratiske polynomiale tendens er f.eks. tydelig i følgende graf, der viser forholdet mellem fortjenesten og antallet af år, produktet har været på markedet: stigning i begyndelsen, top i midten og fald mod slutningen.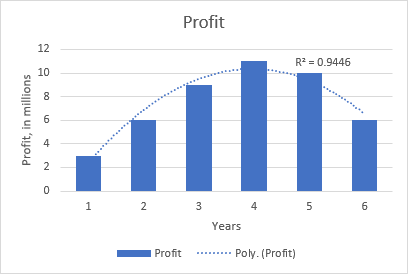

Power trendline

Effekt-trendlinjen ligner meget den eksponentielle kurve, men den har en mere symmetrisk bue. Den bruges ofte til at plotte målinger, der stiger med en vis hastighed.

Der kan ikke tilføjes en power trendline til et Excel-diagram, der indeholder nul eller negative værdier.

Lad os som eksempel tegne en power trendline for at visualisere den kemiske reaktionshastighed. Bemærk R-squared-værdien på 0,9918, hvilket betyder, at vores trendline passer næsten perfekt til dataene.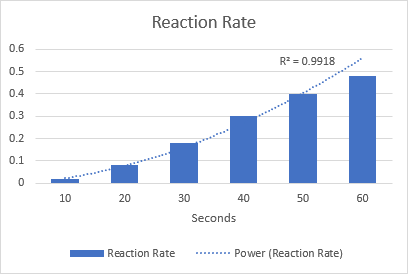

Glidende gennemsnitlig trendlinje

Når datapunkterne i dit diagram har mange op- og nedture, kan en trendlinje med et glidende gennemsnit udjævne de ekstreme udsving i dataværdierne for at vise et mønster mere tydeligt. Excel beregner det glidende gennemsnit af det antal perioder, du angiver (som standard 2), og placerer disse gennemsnitsværdier som punkter i linjen. Jo højere den Periode værdien, jo mere glat er linjen.

Et godt praktisk eksempel er at bruge den glidende gennemsnitstrendlinje til at afsløre udsving i en aktiekurs, som ellers ville være svære at observere.

Du kan finde flere oplysninger i: Sådan tilføjer du en trendlinje for glidende gennemsnit til et Excel-diagram.

Excel-ligninger og formler for trendlinjer

I dette afsnit beskrives de ligninger, som Excel bruger til forskellige trendlinjetyper. Du behøver ikke at opbygge disse formler manuelt, men skal blot bede Excel om at vise trendlinjeligningen i et diagram.

Vi vil også diskutere formlen til at finde hældningen af en tendenslinje og andre koefficienter. Formlerne forudsætter, at du har 2 sæt variabler: uafhængig variabel x og afhængige variabel y I dine regneark kan du bruge disse formler til at få den forudsagte y værdier for enhver given værdi af x .

Af hensyn til konsistensen vil vi bruge det samme datasæt med lidt varierende værdier i alle eksemplerne. Husk dog, at det kun er til demonstrationsformål. I dine rigtige regneark skal du vælge den trendlinjetype, der svarer til din datatype.

Vigtig bemærkning! Trendline-formlerne bør kun bruges med XY-spredningsdiagrammer fordi kun dette diagram viser både x og y akser som numeriske værdier. Du kan finde flere oplysninger i Hvorfor Excel-tendenslinjeligningen måske er forkert.

Ligning og formler for lineær trendlinje

Den lineære trendlinjeligning anvender de mindste kvadraters metoder til at finde den hældning og intercept koefficienter således, at:

Hvor:

• b er den hældning af en trendlinje.
• a er den y-intercept , som er den forventede middelværdi af y når alle x variabler er lig med 0. På et diagram er det det punkt, hvor trendlinjen krydser den y akse.

Til lineær regression indeholder Microsoft Excel særlige funktioner til at få koefficienterne for hældning og skæringspunkt.

Hældning af tendenslinje

b: =SLOPE(y,x)

Y-intercept

a: =INTERCEPT(y,x)

Hvis man antager, at x er B2:B13 og y er C2:C13, og de virkelige formler er som følger:

=HÆLDNING(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

De samme resultater kan opnås ved at bruge LINEST-funktionen som en array-formel Vælg derfor 2 tilstødende celler i samme række, indtast formlen og tryk på Ctrl + Shift + Enter for at fuldføre den:

=LINEST(C2:C13,B2:B13)

Som det fremgår af skærmbilledet nedenfor, er de koefficienter for hældning og intercept, der returneres af formlerne, helt i overensstemmelse med koefficienterne i den lineære trendlinjeligning, der vises i diagrammet, men sidstnævnte er afrundet til 4 decimaler: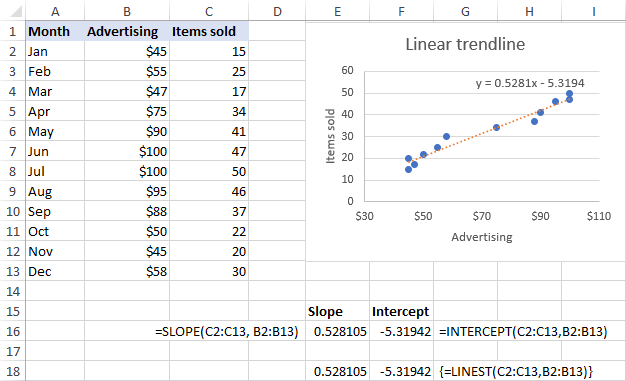

Ligning og formler for eksponentiel trendlinje

For den eksponentielle trendlinje bruger Excel følgende ligning:

Hvor a og b er beregnede koefficienter, og e er den matematiske konstant e (basen for den naturlige logaritme).

Koefficienterne kan beregnes ved hjælp af disse generiske formler:

a: =EXP(INDEX(LINEST(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

For vores datasæt i eksemplet har formlerne følgende formularer:

a: =EXP(INDEX(LINEST(LINEST(LN(C2:C13), B2:B13), 1, 2)))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logaritmisk trendlinje ligning og formler

Her er ligningen for den logaritmiske trendlinje i Excel:

Hvor a og b er konstanter og ln er den naturlige logaritmefunktion.

For at få konstanterne kan du bruge disse generiske formler, som kun adskiller sig fra hinanden ved det sidste argument:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Vi bruger disse til vores datasæt i stikprøven:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polynomial trendlinje ligning og formler

Excel bruger denne ligning til at beregne den polynomiale trendlinje:

Hvor b ₁ ... b ₆ og a er konstanter.

Afhængigt af graden af din polynomiale trendlinje skal du bruge et af følgende sæt formler til at beregne konstanterne.

Quadratisk (2. orden) polynomiel trendlinje

Ligning: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2})), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kubisk (3. orden) polynomiel trendlinje

Ligning: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3})), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3})), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Formlerne for polynomiske trendlinjer af højere grad kan opbygges ved hjælp af samme mønster.

For vores datasæt passer den polynomiale trendlinje af 2. orden bedre, så vi bruger disse formler:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)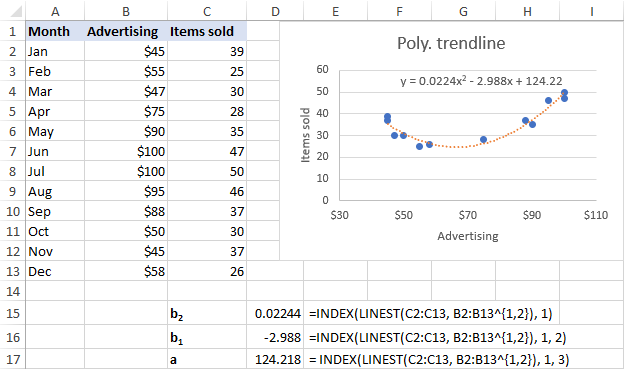

Power trendline ligning og formler

En power trendline i Excel tegnes ud fra denne enkle ligning:

Hvor a og b er konstanter, som kan beregnes med disse formler:

a: =EXP(INDEX(LINEST(LINEST(LN(y), LN(x),,,), 1, 2)))

b: =INDEX(LINEST(LN(y), LN(x),,,), 1)

I vores tilfælde fungerer følgende formler godt:

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,,), 1, 2)))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,,), 1)

Excel trendline-ligningen er forkert - årsager og rettelser

Hvis du mener, at Excel har tegnet en trendlinje forkert, eller hvis den trendlinjeformel, der vises i dit diagram, er forkert, kan de følgende to punkter kaste lidt lys over situationen.

Excel-ligningen for trendlinje er kun korrekt i spredningsdiagrammer

Excel-formler for trendlinjer bør kun bruges med XY-grafer (spredningsgrafer), fordi det kun er i denne diagramtype, at både y-aksen og x-aksen er plottet som numeriske værdier.

I linjediagrammer, kolonne- og søjlediagrammer er numeriske værdier kun plottet på y-aksen. x-aksen repræsenteres af en lineær serie (1, 2, 3,...), uanset om akseetiketterne er tal eller tekst. Når du laver en tendenslinje i disse diagrammer, bruger Excel disse antagne x-værdier i tendenslinjeformlen.

Tallene er afrundede i Excel-ligningen for trendlinjer

For at optage mindre plads i diagrammet viser Excel meget få betydende cifre i en trendlinjeligning. Det er et flot design, men det reducerer formlens nøjagtighed betydeligt, når du manuelt angiver x-værdier i ligningen.

En nem løsning er at vise flere decimaler i ligningen. Alternativt kan du beregne koefficienterne ved at bruge en formel, der svarer til din trendlinjetype, og formatere formelcellerne, så de viser et tilstrækkeligt antal decimaler. Klik på Forøgelse af decimaltal på knappen på Hjem i fanen i Nummer gruppe.

Sådan kan du lave forskellige trendlinjetyper i Excel og få deres ligninger. Jeg takker for læsningen og håber at se dig på vores blog i næste uge!