Neste titorial, atoparás a descrición detallada de todas as opcións de liña de tendencia dispoñibles en Excel e cando usalas. Tamén aprenderá a mostrar unha ecuación de liña de tendencia nun gráfico e atopar a pendente da liña de tendencia.

É moi sinxelo engadir unha liña de tendencia en Excel. O único reto real é escoller o tipo de liña de tendencia que mellor se corresponda co tipo de datos que está a analizar. Neste tutorial, atoparás a descrición detallada de todas as opcións de liña de tendencia dispoñibles en Excel e cando usalas. Se estás a buscar como inserir unha liña de tendencia nun gráfico de Excel, consulta o tutorial da ligazón anterior.

Tipos de liñas de tendencia de Excel

Ao engadir unha liña de tendencia en Excel , tes 6 opcións diferentes para escoller. Ademais, Microsoft Excel permite mostrar unha ecuación da liña de tendencia e un valor R-cadrado nun gráfico:

• A ecuación da liña de tendencia é unha fórmula que atopa a liña que mellor se axuste aos puntos de datos.
• O valor de R cadrado mide a fiabilidade da liña de tendencia: canto máis preto estea R2 a 1, mellor se axusta a liña de tendencia aos datos.

A continuación, atoparás unha breve descrición de cada tipo de liña de tendencia con exemplos de gráficos.

Liña de tendencia lineal

A liña de tendencia lineal é mellor ser úsase con conxuntos de datos lineais cando os puntos de datos dun gráfico semellan unha liña recta. Normalmente, unha liña de tendencia lineal describe un aumento ou caída continuaao longo do tempo.

Por exemplo, a seguinte liña de tendencia lineal mostra un aumento constante das vendas durante 6 meses. E o valor R2 de 0,9855 indica un axuste bastante bo dos valores da liña de tendencia estimada aos datos reais.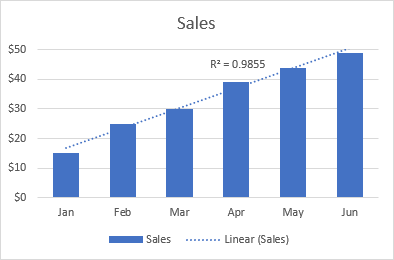

Liña de tendencia exponencial

A liña de tendencia exponencial é unha liña curva que ilustra un aumento ou descenso dos valores dos datos a un ritmo crecente, polo que a liña adoita ser máis curva nun lado. Este tipo de liña de tendencia utilízase a miúdo nas ciencias, por exemplo, para visualizar un crecemento da poboación humana ou un descenso das poboacións de animais salvaxes.

Ten en conta que non se pode crear unha liña de tendencia exponencial para datos que conteñan ceros ou valores negativos.

Un bo exemplo de curva exponencial é a decadencia de toda a poboación de tigres salvaxes da Terra.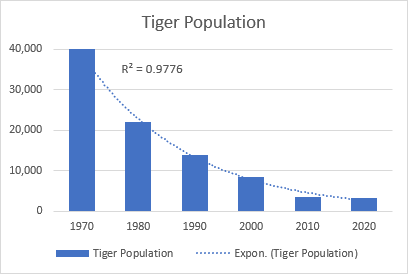

Liña de tendencia logarítmica

A liña de mellor axuste logarítmica úsase xeralmente para trazar datos que aumentan ou diminúen rapidamente e que despois se nivelan. Pode incluír tanto valores positivos como negativos.

Un exemplo de liña de tendencia logarítmica pode ser unha taxa de inflación, que primeiro é cada vez máis alta pero despois dun tempo se estabiliza.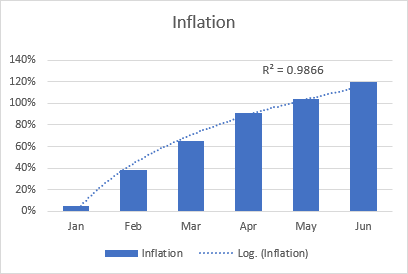

Liña de tendencia polinómica

A liña de tendencia curvilínea polinómica funciona ben para conxuntos de datos grandes con valores oscilantes que teñen máis dunha subida e unha baixada.

Xeralmente, un polinomio clasifícase polo grao do maior expoñente. O grao da liña de tendencia polinómica podetamén se determina polo número de curvas dunha gráfica. Normalmente, unha liña de tendencia polinómica cuadrática ten unha curva (outro ou val), un polinomio cúbico ten 1 ou 2 curvas e un polinomio cuártico ten ata 3 curvas.

Ao engadir unha liña de tendencia polinómica nun gráfico de Excel, especifica o grao escribindo o número correspondente na caixa Orden do panel Formato de liña de tendencia , que é 2 por defecto: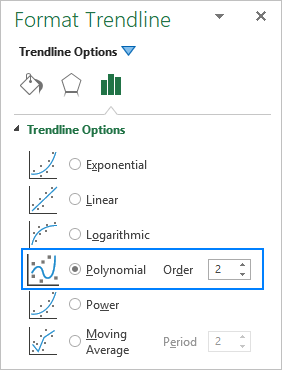

Por exemplo, a tendencia polinómica cuadrática é evidente no seguinte gráfico que amosa a relación entre o beneficio e o número de anos que leva o produto no mercado: suba ao principio, pico no medio e baixa preto do final.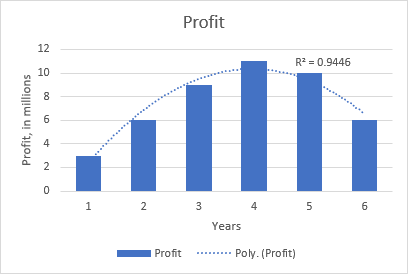

Liña de tendencia de potencia

A liña de tendencia de potencia é moi semellante á curva exponencial, só que ten un arco máis simétrico. Úsase habitualmente para trazar medidas que aumentan a un ritmo determinado.

Non se pode engadir unha liña de tendencia de potencia a un gráfico de Excel que conteña valores cero ou negativos.

A modo de exemplo, debuxemos un liña de tendencia de potencia para visualizar a velocidade da reacción química. Teña en conta o valor R-cadrado de 0,9918, o que significa que a nosa liña de tendencia encaixa case perfectamente cos datos.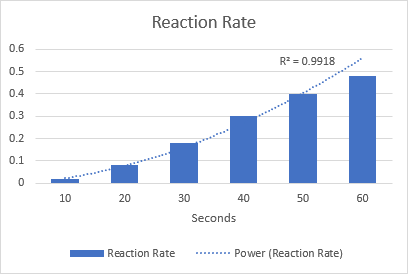

Liña de tendencia media móbil

Cando os puntos de datos do teu gráfico teñen moitos altibaixos, unha liña de tendencia media móbil pode suavizar as flutuacións extremas dos valores dos datos para mostrar un patrón con máis claridade. Para iso, Excel calcula omedia móbil do número de períodos que especifique (2 por defecto) e pon eses valores medios como puntos na liña. Canto maior sexa o valor do Período , máis suave será a liña.

Un bo exemplo práctico é o uso da liña de tendencia da media móbil para revelar as flutuacións do prezo das accións que, doutro xeito, serían difíciles de observar.

Para obter máis información, consulte: Como engadir unha liña de tendencia media móbil a un gráfico de Excel.

Ecuacións e fórmulas de liña de tendencia de Excel

Esta sección describe as ecuacións que utiliza Excel. para diferentes tipos de liñas de tendencia. Non tes que construír estas fórmulas manualmente, simplemente indica a Excel que mostre a ecuación da liña de tendencia nun gráfico.

Ademais, comentaremos a fórmula para atopar a pendente dunha liña de tendencia e outros coeficientes. As fórmulas supoñen que tes 2 conxuntos de variables: variable independente x e variable dependente y . Nas túas follas de traballo, podes usar estas fórmulas para obter os valores previstos de y para calquera valor dado de x .

Para a coherencia, utilizaremos os mesmos datos conxunto con valores lixeiramente variables para todos os exemplos. Non obstante, ten en conta que só é para fins de demostración. Nas túas follas de traballo reais, debes escoller o tipo de liña de tendencia correspondente ao teu tipo de datos.

Nota importante! As fórmulas de liña de tendencia só deben usarse con gráficos de dispersión XY porque só istoo gráfico representa os eixes x e y como valores numéricos. Para obter máis información, consulte Por que a ecuación da liña de tendencia de Excel pode ser incorrecta.

Ecuación da liña de tendencia lineal e fórmulas

A ecuación da liña de tendencia lineal usa os métodos de mínimos cadrados para buscar a pendente e intersección coeficientes tales que:

y = bx + a

Onde:

• b é a pendente dunha liña de tendencia.
• a é a intersección en y , que é o valor medio esperado de y cando todo x as variables son iguais a 0. Nun gráfico, é o punto onde a liña de tendencia cruza o eixe y .

Para a regresión lineal, Microsoft Excel ofrece funcións especiais para obter o pendente e coeficientes de intersección.

Pendente da liña de tendencia

b: =SLOPE(y,x)

Intercepto en Y

a: =INTERCEPT(y,x)

Asumindo que o intervalo x é B2:B13 e o intervalo y é C2:C13, as fórmulas da vida real son as seguintes:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

Os mesmos resultados pódense conseguir empregando a función LINEST como fórmula matricial . Para iso, seleccione 2 celas adxacentes na mesma fila, introduza a fórmula e prema Ctrl + Maiús + Intro para completala:

=LINEST(C2:C13,B2:B13)

Como se mostra na captura de pantalla a continuación, a pendente e a interceptación os coeficientes devoltos polas fórmulas están perfectamente en liña cos coeficientes da ecuación da liña de tendencia lineal mostrada no gráfico, só estes últimos se redondean a 4 decimais: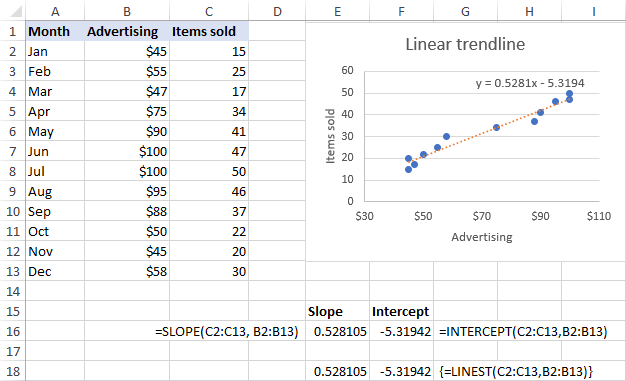

Ecuación e fórmulas da liña de tendencia exponencial

Para a liña de tendencia exponencial, Excel usa a seguinte ecuación:

y = aebx

Onde a e b son coeficientes calculados e e é a constante matemática e (a base do logaritmo natural).

Os coeficientes pódense calcular utilizando estas fórmulas xenéricas:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

Para o noso conxunto de datos de mostra, as fórmulas adoptan a seguinte forma:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Ecuación e fórmulas da liña de tendencia logarítmica

Aquí está a ecuación da liña de tendencia logarítmica en Excel:

y = a*ln(x)+b

Onde a e b son constantes e ln é a función de logaritmo natural.

Para obter as constantes, use estas fórmulas xenéricas, que só difiren no último argumento:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

Para o noso conxunto de datos de mostra, utilizamos estes:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Ecuación da liña de tendencia polinómica e fórmulas

Para calcular a liña de tendencia polinómica, Excel usa esta ecuación:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Onde b ₁ … b ₆ e a son constantes.

Dependendo do grao da túa liña de tendencia polinómica, utiliza un dos seguintes conxuntos de fórmulas para obter as constantes.

Liña de tendencia polinómica cuadrática (2ª orde)

Ecuación: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Liña de tendencia polinómica cúbica (tercera orde)

Ecuación: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

As fórmulas para as liñas de tendencia polinómicas de grao superior pódense construír utilizando o mesmo patrón.

Para o noso conxunto de datos, os conxuntos de liñas de tendencia polinómicas de 2ª orde mellor, polo que estamos a usar estas fórmulas:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)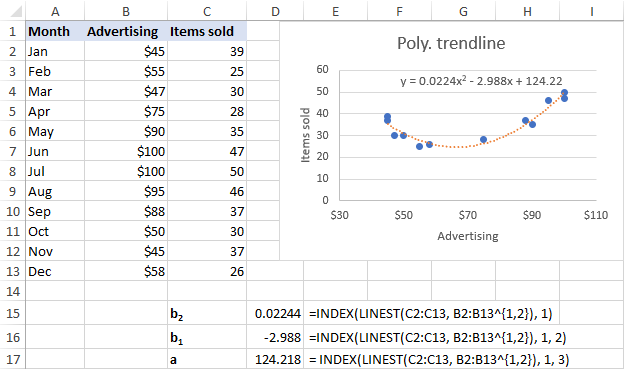

Ecuación e fórmulas da liña de tendencia de potencia

Unha liña de tendencia de potencia en Excel debúxase a partir desta ecuación sinxela:

y = axb

Onde a e b son constantes, que se poden calcular con estas fórmulas:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

No noso caso, as seguintes fórmulas funcionan moi ben :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

A ecuación da liña de tendencia de Excel é incorrecta: razóns e solucións

Se pensas que Excel debuxou unha liña de tendencia incorrectamente ou a fórmula da liña de tendencia que aparece no gráfico é incorrecta, os dous puntos seguintes poden perder algo luz sobre a situación.

A ecuación de liña de tendencia de Excel só é correcta nos gráficos de dispersión

As fórmulas de liña de tendencia de Excel só deben usarse con gráficos XY (dispersión), porque só neste gráfico escribe tanto o eixe y e os eixes x trazan como valores numéricos.

Nos gráficos de liñas, columnas e de barras, os valores numéricos só se representan no eixe y. O eixe x está representado por unha serie lineal (1, 2,3,...) independentemente de que as etiquetas dos eixes sexan números ou texto. Cando crea unha liña de tendencia nestes gráficos, Excel utiliza os valores x asumidos na fórmula da liña de tendencia.

Os números arredondanse na ecuación da liña de tendencia de Excel

Para ocupar menos espazo no gráfico, Excel mostra moi poucos díxitos significativos nunha ecuación de liña de tendencia. Agradable en termos de deseño, reduce significativamente a precisión da fórmula cando forneces manualmente os valores x na ecuación.

Unha solución sinxela é mostrar máis cifras decimais na ecuación. Alternativamente, pode calcular os coeficientes utilizando unha fórmula correspondente ao seu tipo de liña de tendencia e formatar as celas da fórmula para que mostren un número suficiente de decimais. Para iso, só tes que facer clic no botón Aumentar decimal da pestana Inicio do grupo Número .

Así podes crear diferentes tipos de liñas de tendencia. en Excel e obtén as súas ecuacións. Grazas por ler e espero verte no noso blog a vindeira semana!