I denne opplæringen finner du den detaljerte beskrivelsen av alle trendlinjealternativene som er tilgjengelige i Excel og når du skal bruke dem. Du vil også lære hvordan du viser en trendlinjeligning i et diagram og finner hellingen til trendlinjen.

Det er veldig enkelt å legge til en trendlinje i Excel. Den eneste virkelige utfordringen er å velge den trendlinjetypen som best samsvarer med typen data du analyserer. I denne opplæringen finner du den detaljerte beskrivelsen av alle trendlinjealternativene som er tilgjengelige i Excel og når du skal bruke dem. Hvis du leter etter hvordan du setter inn en trendlinje i et Excel-diagram, vennligst sjekk den lenkede opplæringen ovenfor.

Excel-trendlinjetyper

Når du legger til en trendlinje i Excel , har du 6 forskjellige alternativer å velge mellom. I tillegg tillater Microsoft Excel å vise en trendlinjeligning og R-kvadratverdi i et diagram:

• Trendlinjeligning er en formel som finner en linje som passer best til datapunktene.
• R-kvadratverdi måler trendlinjens pålitelighet - jo nærmere R2 er 1, jo bedre passer trendlinjen til dataene.

Nedenfor finner du en kort beskrivelse av hver trendlinjetype med diagrameksempler.

Lineær trendlinje

Den lineære trendlinjen er best å være brukes med lineære datasett når datapunktene i et diagram ligner en rett linje. Vanligvis beskriver en lineær trendlinje en kontinuerlig stigning eller fallover tid.

For eksempel viser følgende lineære trendlinje en jevn økning i salget over 6 måneder. Og R2-verdien på 0,9855 indikerer en ganske god tilpasning av de estimerte trendlinjeverdiene til de faktiske dataene.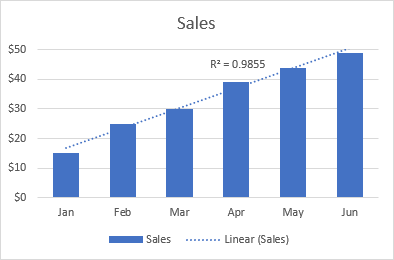

Eksponentiell trendlinje

Den eksponentielle trendlinjen er en buet linje som illustrerer en økning eller fall i dataverdier med økende hastighet, derfor er linjen vanligvis mer buet på den ene siden. Denne trendlinjetypen brukes ofte i vitenskaper, for eksempel for å visualisere en menneskelig populasjonsvekst eller nedgang i dyrelivspopulasjoner.

Vær oppmerksom på at en eksponentiell trendlinje ikke kan opprettes for data som inneholder nuller eller negative verdier.

Et godt eksempel på en eksponentiell kurve er forfallet i hele den ville tigerbestanden på jorden.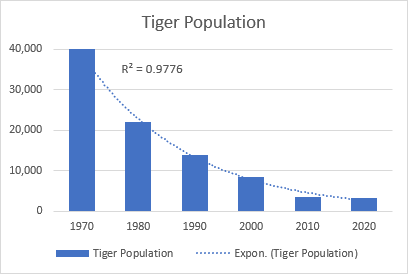

Logaritmisk trendlinje

Den logaritmiske best-fit-linjen brukes vanligvis til å plotte data som raskt øker eller reduseres og deretter flater ut. Den kan inkludere både positive og negative verdier.

Et eksempel på en logaritmisk trendlinje kan være en inflasjonsrate, som først blir høyere, men etter en stund stabiliserer seg.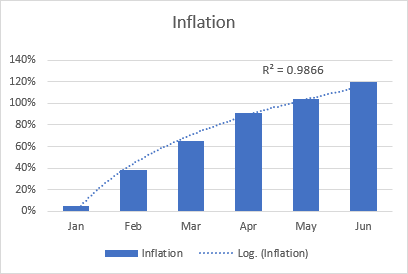

Polynomtrendlinje

Den polynomkurvilineære trendlinjen fungerer godt for store datasett med oscillerende verdier som har mer enn én stigning og fall.

Generelt er et polynom klassifisert etter grad av den største eksponenten. Graden av polynomens trendlinje kanogså bestemmes av antall bøyninger på en graf. Vanligvis har en kvadratisk polynomtrendlinje én bøyning (bakke eller dal), et kubisk polynom har 1 eller 2 bøyninger, og et kvartspolynom har opptil 3 bøyninger.

Når du legger til en polynomtrendlinje i et Excel-diagram, du spesifiserer graden ved å skrive inn det tilsvarende tallet i boksen Ordre i ruten Format trendlinje , som er 2 som standard: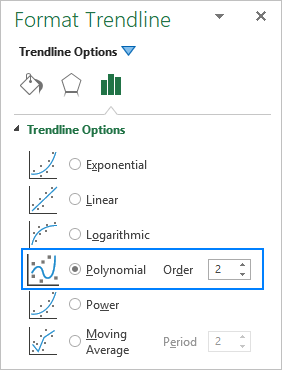

For eksempel den kvadratiske polynomtrenden er tydelig på følgende graf som viser forholdet mellom fortjenesten og antall år produktet har vært på markedet: stigning i begynnelsen, topp i midten og fall mot slutten.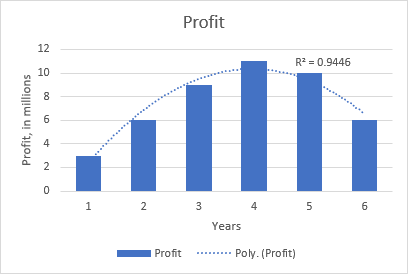

Power trendline

Potentrendlinjen er veldig lik den eksponentielle kurven, bare den har en mer symmetrisk bue. Det brukes ofte til å plotte målinger som øker med en viss hastighet.

En effekttrendlinje kan ikke legges til et Excel-diagram som inneholder null eller negative verdier.

La oss som et eksempel tegne en strømtrendlinje for å visualisere den kjemiske reaksjonshastigheten. Legg merke til R-kvadratverdien på 0,9918, som betyr at trendlinjen vår passer til dataene nesten perfekt.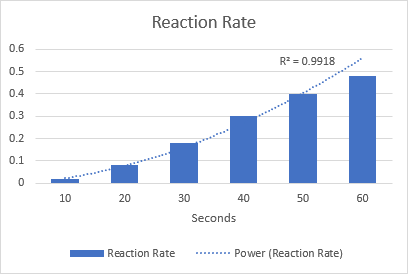

Bevegende gjennomsnittlig trendlinje

Når datapunktene i diagrammet ditt har mange opp- og nedturer, kan en glidende gjennomsnittstrendlinje jevne ut de ekstreme svingningene i dataverdiene for å vise et mønster tydeligere. For dette beregner Excelglidende gjennomsnitt av antall perioder du angir (2 som standard) og setter disse gjennomsnittsverdiene som punkter på linjen. Jo høyere Periode -verdi, desto jevnere er linjen.

Et godt praktisk eksempel er å bruke trendlinjen for glidende gjennomsnitt for å avsløre svingninger i en aksjekurs som ellers ville vært vanskelig å observere.

For mer informasjon, se: Slik legger du til en glidende gjennomsnittstrendlinje til et Excel-diagram.

Excel-trendlinjeligninger og formler

Denne delen beskriver ligningene som Excel bruker for ulike trendlinjetyper. Du trenger ikke å bygge disse formlene manuelt, bare be Excel om å vise trendlinjeligningen i et diagram.

Vi vil også diskutere formelen for å finne helningen til en trendlinje og andre koeffisienter. Formlene forutsetter at du har 2 sett med variabler: uavhengig variabel x og avhengig variabel y . I regnearkene dine kan du bruke disse formlene for å få de anslåtte y -verdiene for alle gitte verdier på x .

For konsistens vil vi bruke de samme dataene satt med litt varierende verdier for alle eksemplene. Vær imidlertid oppmerksom på at det kun er for demonstrasjonsformål. I de virkelige regnearkene dine bør du velge trendlinjetypen som tilsvarer datatypen din.

Viktig merknad! Trendlinjeformlene skal bare brukes med XY-spredningsdiagrammer fordi kun dettediagram plotter både x og y akser som numeriske verdier. For mer informasjon, se Hvorfor Excel-trendlinjeligningen kan være feil.

Lineær trendlinjeligning og formler

Den lineære trendlinjeligningen bruker minste kvadraters metode for å søke hellingen og skjæringspunkt koeffisienter slik at:

y = bx + a

Hvor:

• b er hellingen av en trendlinje.
• a er y-skjæringspunktet , som er den forventede gjennomsnittsverdien av y når alle x -variabler er lik 0. På et diagram er det punktet der trendlinjen krysser y -aksen.

For lineær regresjon tilbyr Microsoft Excel spesielle funksjoner for å få helning og skjæringskoeffisienter.

Helning av trendlinje

b: =SLOPE(y,x)

Y-skjæringspunkt

a: =INTERCEPT(y,x)

Forutsatt at x -området er B2:B13 og y -området er C2:C13, ser de virkelige formlene ut som følger:

=SLOPE(C2:C13, B2:B13)

=INTERCEPT(C2:C13,B2:B13)

De samme resultatene kan oppnås ved å bruke LINJE-funksjonen som en matriseformel . For dette, velg 2 tilstøtende celler i samme rad, skriv inn formelen og trykk Ctrl + Shift + Enter for å fullføre den:

=LINEST(C2:C13,B2:B13)

Som vist på skjermbildet nedenfor, stigningen og avskjæringen koeffisienter returnert av formlene er perfekt i tråd med koeffisientene i den lineære trendlinjeligningen som vises i diagrammet, bare sistnevnte er avrundet til 4 desimaler: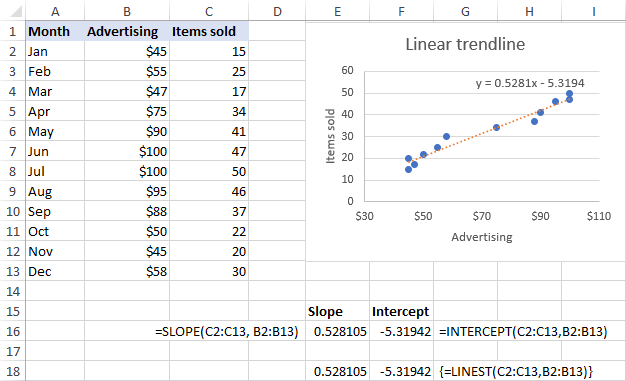

Eksponentiell trendlinjeligning og formler

For den eksponentielle trendlinjen bruker Excel følgende ligning:

y = aebx

Hvor a og b er beregnede koeffisienter og e er den matematiske konstanten e (grunnlaget for den naturlige logaritmen).

Koeffisientene kan beregnes ved å bruke disse generiske formlene:

a: =EXP(INDEX(LINEST(LN(y), x), 1, 2))

b: =INDEX(LINEST(LN(y), x), 1)

For eksempeldatasettet vårt har formlene følgende form:

a: =EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), B2:B13), 1)

Logaritmisk trendlinjeligning og formler

Her er den logaritmiske trendlinjeligningen i Excel:

y = a*ln(x)+b

Hvor a og b er konstanter og ln er den naturlige logaritmefunksjonen.

For å få konstantene, bruk disse generiske formlene, som bare er forskjellige i det siste argumentet:

a: =INDEX(LINEST(y, LN(x)), 1)

b: =INDEX(LINEST(y, LN(x)), 1, 2)

For eksempeldatasettet vårt bruker vi disse:

a: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1)

b: =INDEX(LINEST(C2:C13, LN(B2:B13)), 1, 2)

Polynomtrendlinjeligning og formler

For å regne ut polynomtrendlinjen bruker Excel denne ligningen:

y = b ₆ x6 + … + b ₂ x2 + b ₁ x + a

Hvor b ₁ ... b ₆ og a er konstanter.

Avhengig av graden av polynomtrendlinjen din, bruk ett av følgende sett med formler for å få konstantene.

Kvadratisk (2. orden) polynomtrendlinje

Ligning: y = b ₂ x2+ b ₁ x + a

b ₂ : =INDEX(LINEST(y, x^{1,2}), 1)

b ₁ : =INDEX(LINEST(y, x^{1,2}), 1, 2)

a: =INDEX(LINEST(y, x^{1,2}), 1, 3)

Kubisk (3. orden) polynomtrendlinje

Ligning: y = b ₃ x3 + b ₂ x2+ b ₁ x + a

b ₃ : =INDEX(LINEST(y, x^{1,2,3}), 1)

b ₂ : =INDEX(LINEST(y, x^{1,2,3}), 1, 2)

b ₁ : =INDEX(LINEST(y, x^{1,2,3}), 1, 3)

a: =INDEX(LINEST(y, x^{1,2,3}), 1, 4)

Formlene for polynomtrendlinjer med høyere grad kan bygges ved å bruke det samme mønsteret.

For vårt datasett, 2. ordens polynomtrendlinjesuiter bedre, så vi bruker disse formlene:

b ₂ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)

b ₁ : =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)

a: =INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)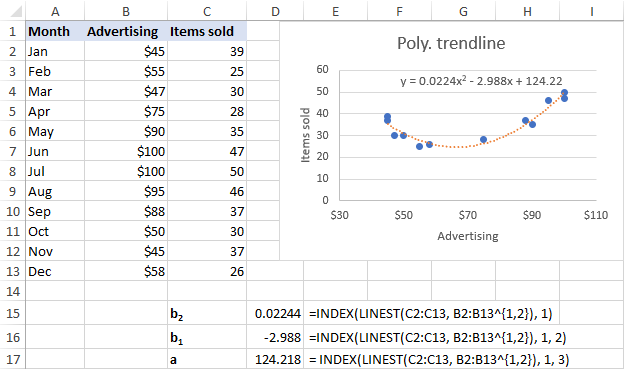

Power trendlinjeligning og formler

En potenstrendlinje i Excel tegnes basert på denne enkle ligningen:

y = axb

Hvor a og b er konstanter, som kan beregnes med disse formlene:

a: =EXP(INDEX(LINEST(LN(y), LN(x),,), 1, 2))

b: =INDEX(LINEST(LN(y), LN(x),,), 1)

I vårt tilfelle fungerer følgende formler en godbit :

a: =EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1, 2))

b: =INDEX(LINEST(LN(C2:C13), LN(B2:B13),,), 1)

Excel-trendlinjeligningen er feil - årsaker og rettinger

Hvis du tror at Excel har tegnet en trendlinje feil eller trendlinjeformelen som vises i diagrammet ditt er feil, kan de følgende to punktene miste noe lys på situasjonen.

Excel-trendlinjeligningen er bare riktig i spredningsdiagrammer

Excel-trendlinjeformler bør kun brukes med XY (sprednings)-grafer fordi bare i dette diagrammet skriver du både y-aksen og x-aksen er plottet som numeriske verdier.

I linjediagrammer, kolonne- og søylediagrammer er numeriske verdier kun plottet på y-aksen. X-aksen er representert av en lineær serie (1, 2,3,...) uavhengig av om akseetikettene er tall eller tekst. Når du lager en trendlinje i disse diagrammene, bruker Excel de antatte x-verdiene i trendlinjeformelen.

Tall er avrundet i Excel-trendlinjeligningen

For å oppta mindre plass i diagrammet, viser Excel svært få signifikante sifre i en trendlinjeligning. Fint designmessig, det reduserer formelens nøyaktighet betraktelig når du manuelt oppgir x-verdier i ligningen.

En enkel løsning er å vise flere desimaler i ligningen. Alternativt kan du beregne koeffisientene ved å bruke en formel som tilsvarer trendlinjetypen din, og formatere formelcellene slik at de viser et tilstrekkelig antall desimaler. For dette klikker du bare på Øk desimal -knappen på Hjem -fanen i Tall -gruppen.

Slik kan du lage forskjellige trendlinjetyper i Excel og få ligningene deres. Jeg takker for at du leser og håper å se deg på bloggen vår neste uke!