টিউটোৰিয়েলত যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ কি, আৰু এক্সেলত কেনেকৈ এটা স্পষ্ট আৰু সহজে বুজিব পৰা CAGR সূত্ৰ বনাব পাৰি সেই বিষয়ে ব্যাখ্যা কৰা হৈছে।

আমাৰ পূৰ্বৰ এটা প্ৰবন্ধত, আমি চক্রবৃদ্ধি সুতৰ শক্তি আৰু ইয়াক এক্সেলত কেনেকৈ গণনা কৰিব লাগে উন্মোচন কৰিলোঁ। আজি আমি আৰু এখোজ আগুৱাই যাম আৰু যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ (CAGR) গণনা কৰাৰ বিভিন্ন উপায় অন্বেষণ কৰিম।

সৰল ভাষাত ক'বলৈ গ'লে, CAGR এ এটা নিৰ্দিষ্ট সময়ৰ ভিতৰত বিনিয়োগৰ ৰিটাৰ্ণ জুখিব। কঠোৰভাৱে ক'বলৈ গ'লে ই কোনো একাউণ্টিং শব্দ নহয়, কিন্তু ইয়াক প্ৰায়ে বিত্তীয় বিশ্লেষক, বিনিয়োগ পৰিচালক আৰু ব্যৱসায়ৰ মালিকসকলে তেওঁলোকৰ ব্যৱসায় কেনেকৈ বিকশিত হৈছে সেইটো জানিবলৈ বা প্ৰতিযোগী কোম্পানীসমূহৰ ৰাজহ বৃদ্ধিৰ তুলনা কৰিবলৈ ব্যৱহাৰ কৰে।

এই টিউটোৰিয়েলত আমি... গণিতত গভীৰভাৱে খন্দা নহ'ব, আৰু এক্সেলত এটা ফলপ্ৰসূ CAGR সূত্ৰ কেনেকৈ লিখিব লাগে তাৰ ওপৰত গুৰুত্ব দিব যিয়ে ৩টা প্ৰাথমিক ইনপুট মানৰ ওপৰত ভিত্তি কৰি যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ গণনা কৰাৰ অনুমতি দিয়ে: বিনিয়োগৰ আৰম্ভণিৰ মূল্য, শেষ মূল্য, আৰু সময়ৰ সময়সীমা।

যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ কি?

যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ (চমুকৈ CAGR) হৈছে এটা বিত্তীয় শব্দ যিয়ে বিনিয়োগৰ গড় বাৰ্ষিক বৃদ্ধিৰ হাৰ জুখিব এটা নিৰ্দিষ্ট সময়ৰ ভিতৰত।

CAGR যুক্তি ভালদৰে বুজিবলৈ, তলৰ উদাহৰণটো চাওঁ আহক। ধৰি লওক, আপুনি আপোনাৰ কোম্পানীটোৰ বিত্তীয় প্ৰতিবেদনত তলৰ সংখ্যাবোৰ দেখিছে:

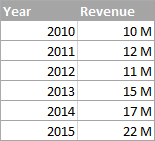
বছৰৰ পিছত বছৰ ধৰি বৃদ্ধিৰ হিচাপ কৰাটো কোনো ডাঙৰ কথা নহয়তলৰ স্ক্ৰীণশ্বটত দেখুওৱাৰ দৰে নিয়মীয়া শতাংশ বৃদ্ধিৰ সূত্ৰ ব্যৱহাৰ কৰি হাৰ:

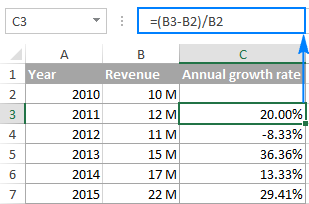
কিন্তু ৫ বছৰৰ ভিতৰত বৃদ্ধিৰ হাৰ দেখুওৱা এটা সংখ্যা কেনেকৈ পাব? ইয়াক গণনা কৰাৰ দুটা উপায় আছে - গড় আৰু যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ। তলত দিয়া কাৰণসমূহৰ বাবে যৌগিক বৃদ্ধিৰ হাৰ এটা উন্নত পৰিমাপ:

• গড় বাৰ্ষিক বৃদ্ধিৰ হাৰ (AAGR) হৈছে বৃদ্ধিৰ হাৰৰ শৃংখলাৰ গাণিতিক গড়, আৰু সেয়াই এটা সাধাৰণ AVERAGE সূত্ৰ ব্যৱহাৰ কৰি সহজে গণনা কৰিব পাৰি। কিন্তু ই যৌগিক প্ৰভাৱক সম্পূৰ্ণৰূপে আওকাণ কৰে আৰু সেয়েহে বিনিয়োগৰ বৃদ্ধি অতিৰিক্তভাৱে অনুমান কৰিব পাৰি।
• যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ (CAGR) হৈছে এটা জ্যামিতিক গড় যিয়ে এটাৰ বাবে লাভৰ হাৰক প্ৰতিনিধিত্ব কৰে বিনিয়োগ যেন প্ৰতি বছৰে স্থিৰ হাৰত বৃদ্ধি পাইছে। অৰ্থাৎ, CAGR হৈছে এটা "মসৃণ" বৃদ্ধিৰ হাৰ যিটো যদি বছৰি যৌগিক কৰা হয়, তেন্তে আপোনাৰ বিনিয়োগে নিৰ্দিষ্ট সময়ৰ ভিতৰত যিখিনি লাভ কৰিছে তাৰ সমতুল্য হ'ব।

CAGR সূত্ৰ

ব্যৱসায়, বিত্ত আৰু বিনিয়োগ বিশ্লেষণত ব্যৱহৃত জেনেৰিক CAGR সূত্ৰটো হ’ল:

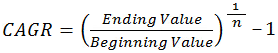
ক’ত:

• BV - বিনিয়োগৰ আৰম্ভণিৰ মূল্য
• EV - বিনিয়োগৰ শেষ মূল্য
• n - সময়ৰ সংখ্যা (যেনে বছৰ, ত্ৰিমাসিক, মাহ, দিন আদি)

তলত দেখুওৱাৰ দৰে স্ক্ৰীণশ্বট, গড় আৰু CAGR সূত্ৰই বিভিন্ন ফলাফল দিয়ে:

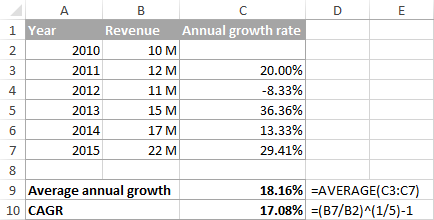
বস্তুবোৰ সহজ কৰিবলৈবুজিবলৈ, তলৰ ছবিখনে দেখুৱাইছে যে কেনেকৈ CAGR গণনা কৰা হয় BV, EV, আৰু n ৰ ক্ষেত্ৰত বিভিন্ন সময়ৰ বাবে:

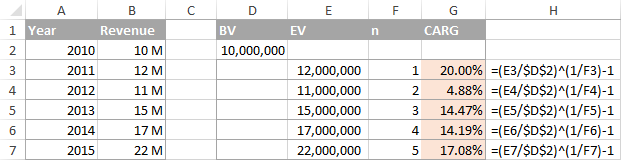
এক্সেলত CAGR কেনেকৈ গণনা কৰিব পাৰি

এতিয়া যেতিয়া আপোনাৰ Compound Annual Growth Rate কি তাৰ এটা মৌলিক ধাৰণা আছে, তেতিয়া চাওঁ আহক আপুনি ইয়াক আপোনাৰ Excel ৱৰ্কশ্বীটত কেনেকৈ গণনা কৰিব পাৰে। সামগ্ৰিকভাৱে CAGR ৰ বাবে এটা Excel সূত্ৰ সৃষ্টি কৰাৰ ৪টা উপায় আছে।

সূত্ৰ ১: Excel ত CAGR কেলকুলেটৰ সৃষ্টি কৰাৰ প্ৰত্যক্ষ উপায়

আলোচনা কৰা জেনেৰিক CAGR সূত্ৰটো জনা ওপৰত, Excel ত এটা CAGR কেলকুলেটৰ সৃষ্টি কৰাটো মিনিটৰ কথা, যদিও চেকেণ্ড নহয়। আপোনাৰ কাৰ্য্যপত্ৰিকাত নিম্নলিখিত মানসমূহ ধাৰ্য্য কৰক:

• BV - বিনিয়োগৰ আৰম্ভণিৰ মূল্য
• EV - বিনিয়োগৰ শেষ মূল্য
• n - সময়ৰ সংখ্যা

আৰু তাৰ পিছত, এটা খালী কোষত CAGR সূত্ৰটো দিয়ক:

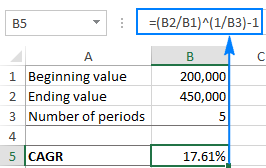
এই উদাহৰণত, BV B1 কোষত, EV B2 ত, আৰু n B3 ত। গতিকে, আমি B5 ত তলত দিয়া সূত্ৰটো দিওঁ:

=(B2/B1)^(1/B3)-1

যদি আপোনাৰ সকলো বিনিয়োগৰ মূল্য কোনো এটা স্তম্ভত তালিকাভুক্ত কৰা হৈছে, তেন্তে আপুনি এটা ডিগ্ৰী যোগ কৰিব পাৰে আপোনাৰ CAGR সূত্ৰলৈ নমনীয়তা আৰু ইয়াক স্বয়ংক্ৰিয়ভাৱে সময়ৰ সংখ্যা গণনা কৰিবলৈ দিয়ক।

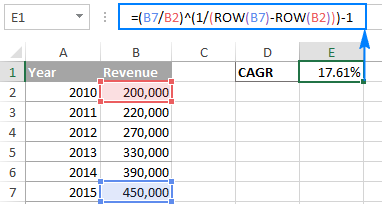
আমাৰ নমুনা কাৰ্য্যপত্ৰিকাত CAGR গণনা কৰিবলৈ সূত্ৰটো হ'ল:

=(B7/B2)^(1/(ROW(B7)-ROW(B2)))-1

<৩><০> টিপচ্। যদি আউটপুট মান এটা দশমিক সংখ্যা হিচাপে প্ৰদৰ্শিত হয়, প্ৰয়োগ কৰকসূত্ৰ কোষলৈ শতাংশ বিন্যাস।

CAGR সূত্ৰ 2: RRI ফাংচন

এক্সেলত যৌগিক বাৰ্ষিক বৃদ্ধিৰ হাৰ গণনা কৰাৰ আটাইতকৈ সহজ উপায় হ'ল RRI ফাংচন ব্যৱহাৰ কৰা, যিটো এটা নিৰ্দিষ্টতকৈ ঋণ বা বিনিয়োগৰ সমতুল্য সুতৰ হাৰ ঘূৰাই দিবলৈ ডিজাইন কৰা হৈছে বৰ্তমানৰ মূল্য, ভৱিষ্যতৰ মূল্য আৰু মুঠ সময়ৰ সংখ্যাৰ ওপৰত ভিত্তি কৰি সময়সীমা:

য'ত:

• Nper হৈছে মুঠ সময়ৰ সংখ্যা।
• Pv হৈছে বিনিয়োগৰ বৰ্তমান মূল্য।
• Fv হৈছে বিনিয়োগৰ ভৱিষ্যত মূল্য।

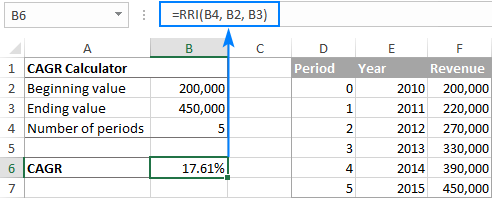
B4 ত nper , B2 ত pv আৰু B3 ত fv ৰ সৈতে, সূত্ৰটোৱে এই ৰূপ লয়:

=RRI(B4, B2, B3)

CAGR সূত্ৰ 3: POWER ফাংচন

এক্সেলত CAGR গণনা কৰাৰ আন এটা দ্ৰুত আৰু পোনপটীয়া উপায় হ'ল POWER ফাংচন ব্যৱহাৰ কৰা যিয়ে এটা সংখ্যাৰ ফলাফল ঘূৰাই দিয়ে POWER ফাংচনৰ বাক্যবিন্যাস নিম্নলিখিত:

য'ত সংখ্যা হৈছে ভিত্তি সংখ্যা, আৰু power হৈছে ভিত্তি সংখ্যা বৃদ্ধি কৰিবলৈ ঘাত to.

POWER ফাংচনৰ ওপৰত ভিত্তি কৰি এটা Excel CAGR কেলকুলেটৰ বনাবলৈ, যুক্তিসমূহ এইদৰে সংজ্ঞায়িত কৰক:

• সংখ্যা - শেষ মান (EV) / আৰম্ভণি মান (BV)
• শক্তি - 1/পিৰিয়ডৰ সংখ্যা (n)

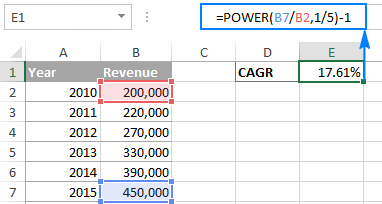
আৰু ইয়াত আমাৰ POWERful CAGR সূত্ৰটো কাৰ্য্যত আছে:

=POWER(B7/B2,1/5)-1

প্ৰথম উদাহৰণৰ দৰে, আপুনি পাৰেআপোনাৰ বাবে পিৰিয়ডৰ সংখ্যা গণনা কৰিবলৈ ROW ফাংচন আছে:

=POWER(B7/B2,1/(ROW(B7)-ROW(B2)))-1

CAGR সূত্ৰ 4: RATE ফাংচন

এক্সেলত CAGR গণনা কৰাৰ বাবে আৰু এটা পদ্ধতি হৈছে RATE ব্যৱহাৰ কৰা ফাংচন যিয়ে এটা বাৰ্ষিকীৰ প্ৰতিটো সময়ৰ সুতৰ হাৰ ঘূৰাই দিয়ে।

প্ৰথম দৃষ্টিত, RATE ফাংচনৰ বাক্যবিন্যাস a দেখা যায় কিন্তু আপুনি এবাৰ যুক্তিসমূহ বুজি পালে, আপুনি Excel ত CAGR গণনা কৰিবলৈ এই ধৰণে ভাল পাব পাৰে।

• Nper - বাৰ্ষিকীৰ বাবে মুঠ পেমেণ্টৰ সংখ্যা, অৰ্থাৎ সংখ্যা ঋণ বা বিনিয়োগ পৰিশোধ কৰিবলগীয়া সময়ৰ। প্ৰয়োজনীয়।
• Pmt - প্ৰতিটো সময়ছোৱাত কৰা ধনৰ পৰিমাণ। যদি বাদ দিয়া হয়, fv যুক্তিটো যোগান ধৰিব লাগিব।
• Pv - বিনিয়োগৰ বৰ্তমান মূল্য। প্ৰয়োজনীয়।
• Fv - nper পেমেণ্টৰ শেষত বিনিয়োগৰ ভৱিষ্যত মূল্য। যদি বাদ দিয়া হয়, সূত্ৰটোৱে অবিকল্পিত মান 0 লয়।
• ধৰণ - এটা বৈকল্পিক মান যি পেমেন্ট কেতিয়া দিব লাগে তাক সূচায়:
  • 0 (অবিকল্পিত) - পেমেন্টসমূহ সময়সীমাৰ শেষত পৰিশোধ কৰিব লাগিব।
  • 1 - সময়সীমাৰ আৰম্ভণিতে ধন পৰিশোধ কৰিব লাগিব।
• আনুমানিক - কিহৰ বাবে আপোনাৰ অনুমান হাৰ হ'ব পাৰে। যদি বাদ দিয়া হয়, তেন্তে ইয়াক ১০% বুলি ধৰা হয়।

RATE ফাংচনক এটা CAGR গণনা সূত্ৰলৈ ৰূপান্তৰিত কৰিবলৈ, আপুনি 1st (nper), 3rd (pv) আৰু 4th (fv) যোগান ধৰিব লাগিব। এই ধৰণে যুক্তিসমূহ:

মই আপোনাক সোঁৱৰাই দিম যে:

• BV হৈছে... বিনিয়োগৰ আৰম্ভণিৰ মূল্য
• EV হৈছে বিনিয়োগৰ শেষ মূল্য
• n হৈছে সময়ৰ সংখ্যা

টোকা। আৰম্ভণি মান (BV) এটা ঋণাত্মক সংখ্যা হিচাপে ধাৰ্য্য কৰাটো নিশ্চিত কৰক, অন্যথা আপোনাৰ CAGR সূত্ৰই এটা #NUM ঘূৰাই দিব! আঁসোৱাহ.

এই উদাহৰণত যৌগিক বৃদ্ধিৰ হাৰ গণনা কৰিবলৈ, সূত্ৰটো হ'ল:

=RATE(5,,-B2,B7)

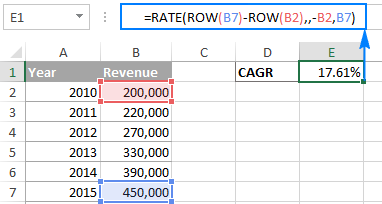
নিজকে পিৰিয়ডৰ সংখ্যা নিজে গণনা কৰাৰ কষ্টৰ পৰা ৰক্ষা কৰিবলৈ, আপুনি ROW পাব পাৰে ফাংচনে আপোনাৰ বাবে ইয়াক গণনা কৰক:

=RATE(ROW(B7)-ROW(B2),,-B2,B7)

CAGR সূত্ৰ 5: IRR ফাংচন

এক্সেলত IRR ফাংচনে ৰ আভ্যন্তৰীণ হাৰ ঘূৰাই দিয়ে নিয়মীয়া সময়ৰ ব্যৱধানত (অৰ্থাৎ দিন, মাহ, ত্ৰিমাসিক, বছৰ আদি) ঘটা নগদ ধনৰ প্ৰবাহৰ শৃংখলাৰ বাবে ৰিটাৰ্ণ। ইয়াৰ তলত দিয়া বাক্যবিন্যাস আছে:

ক'ত:

• মান - নগদ ধনৰ প্ৰবাহক প্ৰতিনিধিত্ব কৰা সংখ্যাৰ এটা পৰিসৰ। পৰিসীমাত অন্ততঃ এটা ঋণাত্মক আৰু অন্ততঃ এটা ধনাত্মক মান থাকিব লাগিব।
• [অনুমান] - এটা বৈকল্পিক যুক্তি যি আপোনাৰ অনুমানক প্ৰতিনিধিত্ব কৰে যে ৰিটাৰ্ণৰ হাৰ কিমান হ'ব পাৰে। যদি বাদ দিয়া হয়, অবিকল্পিত মান 10% লোৱা হয়।

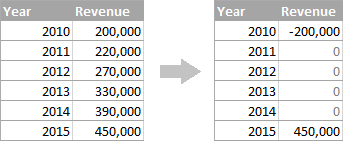
যিহেতু Excel IRR ফাংচনটো যৌগিক বৃদ্ধিৰ হাৰ গণনাৰ বাবে সঠিকভাৱে ডিজাইন কৰা হোৱা নাই, আপুনি মূল তথ্যক এইদৰে পুনৰ আকৃতি দিব লাগিব:

• বিনিয়োগৰ আৰম্ভণিৰ মূল্য ক হিচাপে প্ৰৱেশ কৰিব লাগেঋণাত্মক সংখ্যা।
• বিনিয়োগৰ শেষ মূল্য এটা ধনাত্মক সংখ্যা।
• সকলো মধ্যৱৰ্তী মান শূন্য।

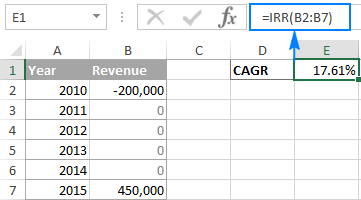
এবাৰ আপোনাৰ উৎস তথ্য পুনৰ সংগঠিত কৰা হৈছে, আপুনি এই সৰল সূত্ৰৰ সৈতে CAGR গণনা কৰিব পাৰে:

=IRR(B2:B7)

য'ত B2 হৈছে আৰম্ভণিৰ মান আৰু B7 হৈছে বিনিয়োগৰ শেষ মূল্য:

বাৰু, এইদৰেই আপুনি Excel ত CAGR গণনা কৰিব পাৰে। যদি আপুনি উদাহৰণসমূহ নিবিড়ভাৱে অনুসৰণ কৰি আহিছে, তেন্তে আপুনি হয়তো লক্ষ্য কৰিছে যে সকলো ৪টা সূত্ৰই একে ফলাফল দিয়ে - ১৭.৬১%। সূত্ৰসমূহ ভালদৰে বুজিবলৈ আৰু সম্ভৱতঃ বিপৰীত অভিযন্তা কৰিবলৈ, আপুনি তলৰ নমুনা কাৰ্য্যপত্ৰিকাখন ডাউনলোড কৰিবলৈ আদৰণি জনোৱা হৈছে। মই আপোনাক পঢ়াৰ বাবে ধন্যবাদ জনাইছো আৰু অহা সপ্তাহত আমাৰ ব্লগত আপোনাক লগ পাম বুলি আশা কৰিছো!

ডাউনল'ডৰ বাবে অনুশীলন কাৰ্য্যপুস্তিকা

CAGR গণনা সূত্ৰ (.xlsx ফাইল)