Þegar þú greinir töluleg gögn gætirðu oft verið að leita að einhverri leið til að fá „venjulegt“ gildi. Í þessu skyni er hægt að nota svokallaða mælingar á miðlægri tilhneigingu sem tákna eitt gildi sem auðkennir miðlæga stöðu innan gagnasafns eða, tæknilegra, miðju eða miðju í tölfræðilegri dreifingu. Stundum eru þær einnig flokkaðar sem yfirlitstölfræði.

Þrír helstu mælikvarðar á miðlæga tilhneigingu eru Meðaltal , Miðgildi og Mode . Þeir eru allir fullgildir mælikvarðar á miðlæga staðsetningu, en hver gefur mismunandi vísbendingu um dæmigert gildi og við mismunandi aðstæður er réttara að nota suma mælikvarða en aðra.

Hvernig á að reikna meðaltal. í Excel

Reiknað meðaltal , einnig nefnt meðaltal , er líklega mælikvarðinn sem þú þekkir best. Meðaltalið er reiknað með því að leggja saman hóp talna og deila síðan summu með fjölda þeirra talna.

Til dæmis, til að reikna meðaltal talna {1, 2, 2, 3, 4, 6 }, leggurðu þau saman og deilir svo summunni með 6, sem gefur 3: (1+2+2+3+4+6)/6=3.

Í Microsoft Excel getur meðaltalið er reiknað með því að nota eina af eftirfarandi föllum:

• AVERAGE- skilar meðaltali af tölum.
• AVERAGEA - skilar meðaltali hólfs með hvaða gögnum sem er (tölur, Boolean og textagildi) ).
• AVERAGEIF - finnur meðaltal af tölum út frá aeinni viðmiðun.
• AVERAGEIFS - finnur meðaltal af tölum byggt á mörgum forsendum.

Fylgdu tenglum hér að ofan fyrir ítarlegar leiðbeiningar. Til að fá hugmyndafræðilega hugmynd um hvernig þessar aðgerðir virka skaltu íhuga eftirfarandi dæmi.

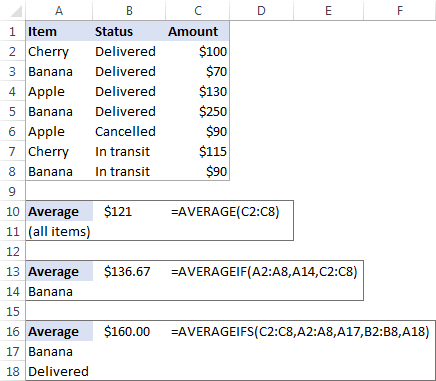
Í söluskýrslu (vinsamlegast sjáðu skjámyndina hér að neðan), að því gefnu að þú viljir fá meðaltal gilda í hólfum C2:C8. Til þess skaltu nota þessa einföldu formúlu:

=AVERAGE(C2:C8)

Til að fá meðaltal af aðeins "Banana" sölu skaltu nota AVERAGEIF formúlu:

=AVERAGEIF(A2:A8, "Banana", C2:C8)

Til að reikna meðaltalið út frá 2 skilyrðum, td meðaltali „Banana“ sölu með stöðunni „Afhent“, notaðu AVERAGEIFS:

=AVERAGEIFS(C2:C8,A2:A8, "Banana", B2:B8, "Delivered")

Þú getur líka slegið inn skilyrði þín í aðskildum hólfum , og vísaðu í þær frumur í formúlunum þínum, svona:

Hvernig á að finna miðgildi í Excel

Miðgildi er miðgildi í hópi talna, sem raðað er í hækkandi eða lækkandi röð, þ.e.a.s. helmingur talna er stærri en miðgildi og helmingur tölur minni en miðgildi. Til dæmis er miðgildi gagnasafnsins {1, 2, 2, 3, 4, 6, 9} 3.

Þetta virkar fínt þegar það eru odd fjölda gilda í hópnum. En hvað ef þú ert með jafnan fjölda gilda? Í þessu tilviki er miðgildið reiknað meðaltal (meðaltal) miðgildanna tveggja. Til dæmis er miðgildi {1, 2, 2, 3, 4, 6} 2,5. Til að reikna það út tekur þú 3. og 4. gildií gagnasafninu og meðaltal þeirra til að fá miðgildi upp á 2,5.

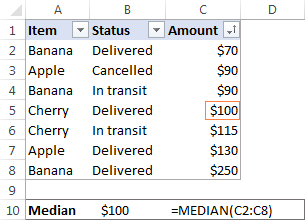
Í Microsoft Excel er miðgildi reiknað með því að nota MEDIAN fallið. Til dæmis, til að fá miðgildi allra upphæða í söluskýrslu okkar, notaðu þessa formúlu:

=MEDIAN(C2:C8)

Til að gera dæmið meira lýsandi hef ég raðað tölunum í dálki C í hækkandi röð (þó það sé í raun ekki nauðsynlegt til að Excel miðgildisformúlan virki):

Öfugt við meðaltalið býður Microsoft Excel ekki upp á neina sérstaka aðgerð til að reikna miðgildi með einum eða fleiri skilyrði. Hins vegar geturðu "hermt eftir" virkni MEDIANIF og MEDIANIFS með því að nota samsetningu tveggja eða fleiri aðgerða eins og sýnt er í þessum dæmum:

• MEDIAN IF formúla (með einu skilyrði)
• MEDIAN IFS formúla (með mörgum forsendum)

Hvernig á að reikna ham í Excel

Hámi er algengasta gildið í gagnasafninu. Þó að meðaltal og miðgildi krefjist útreikninga, er hægt að finna stillingargildi einfaldlega með því að telja hversu oft hvert gildi kemur fyrir.

Til dæmis, háttur gildisafnsins {1, 2, 2, 3 , 4, 6} er 2. Í Microsoft Excel er hægt að reikna út ham með því að nota fallið með sama nafni, MODE fallið. Fyrir sýnishornsgagnasettið okkar er formúlan svona:

=MODE(C2:C8)

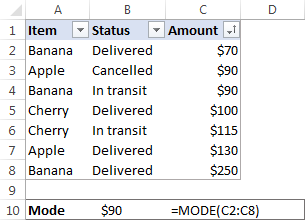
Í aðstæðum þegar það eru tvær eða fleiri stillingar í gagnasettinu þínu, Excel MODE virkamun skila lægsta stillingunni .

Meðaltal vs miðgildi: hvor er betri?

Almennt er enginn "besti" mælikvarði á miðlæga tilhneigingu. Hvaða mælikvarði á að nota fer aðallega eftir því hvers konar gögnum þú ert að vinna með sem og skilningi þínum á „dýpíska gildinu“ sem þú ert að reyna að áætla.

Fyrir samhverfa dreifingu (í hvaða gildi koma fyrir á reglulegri tíðni), eru meðaltal, miðgildi og háttur eins. Fyrir skekkta dreifingu (þar sem lítið er um mjög há eða lág gildi) geta þrír mælikvarðar á miðlæga tilhneigingu verið mismunandi.

Þar sem meðaltalið er er fyrir miklum áhrifum af skekktum gögnum og frávikum (óvenjuleg gildi sem eru verulega frábrugðin restinni af gögnunum), miðgildi er ákjósanlegur mælikvarði á miðlæga tilhneigingu fyrir ósamhverfa dreifingu .

Til dæmis er almennt viðurkennt að miðgildið sé betra en meðaltalið til að reikna út venjuleg laun . Hvers vegna? Besta leiðin til að skilja þetta væri út frá dæmi. Vinsamlega skoðaðu nokkur dæmi um laun fyrir algeng störf:

• Rafmagnari - $20/klst.
• Hjúkrunarfræðingur - $26/klst.
• Lögreglumaður - $47/klst.
• Sölustjóri - $54/klst.
• Framleiðsluverkfræðingur - $63/klst.

Nú skulum við reikna meðaltalið (meðaltal): Tölum saman ofangreindar tölur og deilum með 5: (20+26+47+54+63)/5=42. Þannig að meðallaun eru $42/klst. TheMiðgildi launa er $47/klst. og það er lögreglumaðurinn sem fær þau (1/2 laun eru lægri og 1/2 hærri). Jæja, í þessu tiltekna tilviki gefa meðaltalið og miðgildið svipaðar tölur.

En við skulum sjá hvað gerist ef við lengjum launalistann með því að taka með fræga manneskju sem þénar til dæmis um 30 milljónir dollara á ári, sem er u.þ.b. $14.500/klst. Núna verða meðallaun $2.451,67/klst., laun sem enginn fær! Aftur á móti breytist miðgildið ekki marktækt af þessu eina útlægi, það er $50,50/klst. er ekki svo sterk fyrir áhrifum af óeðlilegum launum.

Svona reiknarðu meðaltal, miðgildi og ham í Excel. Ég þakka þér fyrir lesturinn og vonast til að sjá þig á blogginu okkar í næstu viku!