När du analyserar numeriska data kan du ofta leta efter ett sätt att få fram det "typiska" värdet. För detta ändamål kan du använda den så kallade mått på central tendens som representerar ett enda värde som identifierar den centrala positionen i en datamängd eller, mer tekniskt sett, mitten eller centrum i en statistisk fördelning. Ibland klassificeras de också som sammanfattande statistik.

De tre viktigaste måtten på central tendens är Medelvärde , Median och Läge De är alla giltiga mått på centralorten, men alla ger en annan indikation på ett typiskt värde, och under olika omständigheter är vissa mått lämpligare att använda än andra.

Hur man beräknar medelvärdet i Excel

Aritmetiskt medelvärde , även kallad genomsnittligt Medelvärdet beräknas genom att summera en grupp tal och sedan dividera summan med antalet tal.

För att beräkna medelvärdet av talen {1, 2, 2, 2, 3, 4, 6} adderar du dem och delar sedan summan med 6, vilket ger 3: (1+2+2+2+3+3+4+6)/6=3.

I Microsoft Excel kan medelvärdet beräknas med hjälp av en av följande funktioner:

• AVERAGE - returnerar ett genomsnitt av siffror.
• AVERAGEA - returnerar ett genomsnitt av celler med valfri data (siffror, booleska värden och textvärden).
• AVERAGEIF - hittar ett medelvärde av siffror baserat på ett enda kriterium.
• AVERAGEIFS - hittar ett genomsnitt av siffror baserat på flera kriterier.

För de ingående handledningarna följer du länkarna ovan. För att få en konceptuell uppfattning om hur dessa funktioner fungerar kan du ta följande exempel.

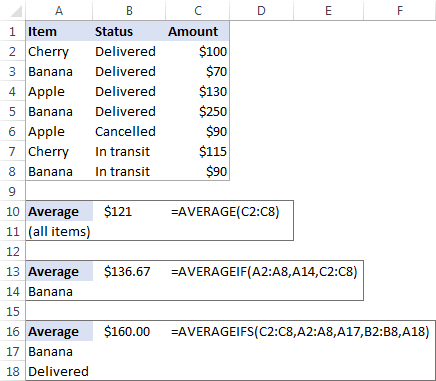
I en försäljningsrapport (se skärmbilden nedan) antar vi att du vill få fram medelvärdet av värdena i cellerna C2:C8. Använd den här enkla formeln för detta:

=GENOMSNITT(C2:C8)

Om du vill få fram ett genomsnitt av endast försäljningen av "Banana" använder du formeln AVERAGEIF:

=AVERAGEIF(A2:A8, "Banana", C2:C8)

Om du vill beräkna medelvärdet baserat på 2 villkor, till exempel medelvärdet av försäljningen av "Banana" med status "Levererad", använder du AVERAGEIFS:

=AVERAGEIFS(C2:C8,A2:A8, "Banana", B2:B8, "Delivered")

Du kan också skriva in villkoren i separata celler och hänvisa till dessa celler i formlerna, så här:

Hur man hittar medianen i Excel

Median är det mittersta värdet i en grupp av siffror som är ordnade i stigande eller fallande ordning, dvs. hälften av siffrorna är större än medianen och hälften av siffrorna är mindre än medianen. Exempelvis är medianen för datamängden {1, 2, 2, 3, 4, 6, 9} 3.

Detta fungerar bra när det finns ett udda antal värden i gruppen. Men vad händer om du har ett även I det här fallet är medianen det aritmetiska medelvärdet av de två mittersta värdena. Medianen för {1, 2, 2, 3, 4, 6} är t.ex. 2,5. För att beräkna medianen tar man det tredje och fjärde värdet i datamängden och beräknar medelvärdet av dem för att få fram en median på 2,5.

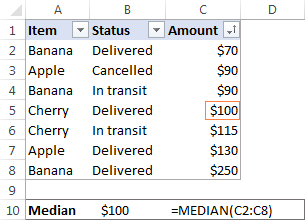
I Microsoft Excel beräknas medianen med hjälp av funktionen MEDIAN. Om du till exempel vill få fram medianen för alla belopp i vår försäljningsrapport använder du den här formeln:

=MEDIAN(C2:C8)

För att göra exemplet mer illustrativt har jag sorterat siffrorna i kolumn C i stigande ordning (även om det egentligen inte krävs för att Excel-formeln Median ska fungera):

I motsats till genomsnittet har Microsoft Excel ingen särskild funktion för att beräkna medianen med ett eller flera villkor. Du kan dock "efterlikna" funktionerna i MEDIANIF och MEDIANIFS genom att använda en kombination av två eller flera funktioner som visas i dessa exempel:

• Formeln MEDIAN IF (med ett villkor)
• Formeln MEDIAN IFS (med flera kriterier)

Hur man beräknar läge i Excel

Läge är det mest frekvent förekommande värdet i datasetet. Medan medelvärdet och medianen kräver vissa beräkningar, kan ett modalvärde hittas helt enkelt genom att räkna hur många gånger varje värde förekommer.

Till exempel är modus för mängden värden {1, 2, 2, 3, 4, 6} 2. I Microsoft Excel kan du beräkna ett modus med hjälp av funktionen med samma namn, MODE-funktionen. För vårt datamaterial ser formeln ut på följande sätt:

=MODE(C2:C8)

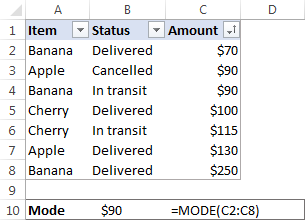
I situationer där det finns två eller flera lägen i din datamängd, kommer Excel MODE-funktionen att återge den lägsta läge .

Medelvärde vs. median: vilket är bäst?

I allmänhet finns det inget "bästa" mått på central tendens. Vilket mått du ska använda beror främst på vilken typ av data du arbetar med och hur du förstår det "typiska värdet" som du försöker uppskatta.

För en symmetrisk fördelning (där värdena uppträder med regelbundna frekvenser) är medelvärdet, medianen och läget desamma. För en snedställd distribution (där det finns ett fåtal extremt höga eller låga värden) kan de tre måtten på central tendens vara olika.

Eftersom medelvärdet påverkas kraftigt av snedställda data och outliers (icke-typiska värden som skiljer sig avsevärt från resten av data), Median är det föredragna måttet på central tendens för en asymmetrisk fördelning .

Det är till exempel allmänt accepterat att medianen är bättre än medelvärdet för att beräkna en typisk lön . Varför? Det bästa sättet att förstå detta är med hjälp av ett exempel. Ta en titt på några exempel på löner för vanliga jobb:

• Elektriker - 20 dollar/timme
• Sjuksköterska - 26 dollar/timme
• Polis - 47 dollar/timme
• Försäljningschef - 54 dollar/timme
• Tillverkningsingenjör - 63 dollar/timme

Låt oss nu beräkna genomsnittet (medelvärdet): addera ovanstående siffror och dela med 5: (20+26+47+54+63)/5=42. Så den genomsnittliga lönen är 42 dollar/timme. Medianlönen är 47 dollar/timme, och det är polisen som tjänar den (1/2 av lönerna är lägre och 1/2 av lönerna är högre). I det här fallet ger medelvärdet och medianen liknande siffror.

Men låt oss se vad som händer om vi utökar listan över löner med en kändis som tjänar till exempel 30 miljoner dollar per år, vilket motsvarar ungefär 14 500 dollar i timmen. Nu blir genomsnittslönen 2 451,67 dollar i timmen, en lön som ingen tjänar! Medianen däremot förändras inte nämnvärt av denna enda utbrytare, den är 50,50 dollar i timmen.

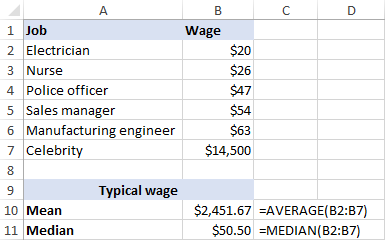
Medianen ger en bättre bild av vad människor vanligtvis tjänar eftersom den inte påverkas så starkt av onormala löner.

Så här räknar du ut medelvärde, median och läge i Excel. Tack för att du läste och hoppas att vi ses på vår blogg nästa vecka!