Når du analyserer numeriske data, kan du ofte søge efter en måde at få den "typiske" værdi på. Til dette formål kan du bruge den såkaldte mål for central tendens der repræsenterer en enkelt værdi, som identificerer den centrale position i et datasæt eller, mere teknisk, midten eller centrum i en statistisk fordeling. Nogle gange klassificeres de også som summariske statistikker.

De tre vigtigste mål for den centrale tendens er Gennemsnitlig , Median og Tilstand De er alle gyldige mål for central beliggenhed, men de giver hver især en anden indikation af en typisk værdi, og under forskellige omstændigheder er nogle mål mere hensigtsmæssige at anvende end andre.

Sådan beregnes gennemsnit i Excel

Aritmetisk gennemsnit , også kaldet gennemsnit Gennemsnittet beregnes ved at lægge en gruppe af tal sammen og derefter dividere summen med antallet af disse tal.

For at beregne gennemsnittet af tallene {1, 2, 2, 2, 3, 4, 6} skal man f.eks. lægge dem sammen og derefter dividere summen med 6, hvilket giver 3: (1+2+2+2+3+3+4+6)/6=3.

I Microsoft Excel kan gennemsnittet beregnes ved at bruge en af følgende funktioner:

• AVERAGE - returnerer et gennemsnit af tal.
• AVERAGEA - returnerer et gennemsnit af celler med alle data (tal, boolske værdier og tekstværdier).
• AVERAGEIF - finder et gennemsnit af tal baseret på et enkelt kriterium.
• AVERAGEIFS - finder et gennemsnit af tal baseret på flere kriterier.

Følg ovenstående links for at få uddybende vejledninger. For at få en idé om, hvordan disse funktioner fungerer, kan du se på følgende eksempel.

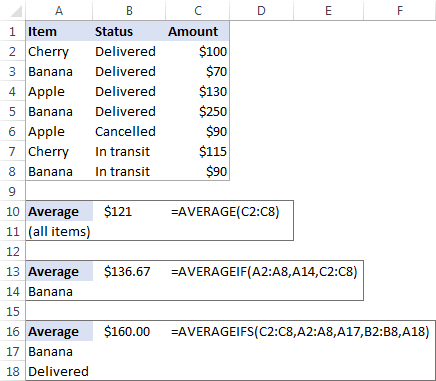
Hvis du i en salgsrapport (se skærmbilledet nedenfor) ønsker at få gennemsnittet af værdierne i cellerne C2:C8, skal du bruge denne enkle formel:

=GENNEMSNIT(C2:C8)

For at få gennemsnittet af kun "Banana"-salget skal du bruge en AVERAGEIF-formel:

=AVERAGEIF(A2:A8, "Banana", C2:C8)

Hvis du vil beregne gennemsnittet baseret på 2 betingelser, f.eks. gennemsnittet af salg af "Bananer" med status "Leveret", skal du bruge AVERAGEIFS:

=AVERAGEIFS(C2:C8,A2:A8, "Banana", B2:B8, "Delivered")

Du kan også indtaste dine betingelser i separate celler og henvise til disse celler i dine formler, f.eks. på denne måde:

Sådan finder du medianen i Excel

Median er den midterste værdi i en gruppe af tal, som er arrangeret i stigende eller faldende rækkefølge, dvs. halvdelen af tallene er større end medianen og halvdelen af tallene er mindre end medianen. F.eks. er medianen for datasættet {1, 2, 2, 3, 4, 6, 9} 3.

Dette fungerer fint, når der er et ulige antal værdier i gruppen. Men hvad nu, hvis du har et selv I dette tilfælde er medianen det aritmetiske gennemsnit af de to midterste værdier. F.eks. er medianen for {1, 2, 2, 3, 4, 6} 2,5. For at beregne den tager man den tredje og fjerde værdi i datasættet og beregner gennemsnittet af dem for at få en median på 2,5.

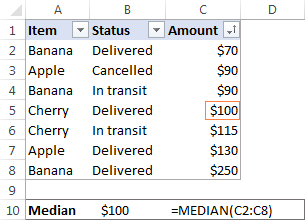
I Microsoft Excel beregnes en median ved hjælp af funktionen MEDIAN. For eksempel skal du bruge denne formel for at få medianen af alle beløb i vores salgsrapport:

=MEDIAN(C2:C8)

For at gøre eksemplet mere illustrativt har jeg sorteret tallene i kolonne C i stigende rækkefølge (selv om det faktisk ikke er nødvendigt for at Excel-formlen Median skal fungere):

I modsætning til gennemsnit har Microsoft Excel ikke nogen særlig funktion til at beregne medianen med en eller flere betingelser. Du kan dog "efterligne" funktionaliteten af MEDIANIF og MEDIANIFS ved at bruge en kombination af to eller flere funktioner som vist i disse eksempler:

• MEDIAN IF-formel (med én betingelse)
• MEDIAN IFS-formel (med flere kriterier)

Sådan beregnes tilstand i Excel

Tilstand er den hyppigst forekommende værdi i datasættet. Mens middelværdien og medianen kræver nogle beregninger, kan man finde en modusværdi ved blot at tælle antallet af gange, hver værdi forekommer.

For eksempel er modus for værdimængden {1, 2, 2, 2, 3, 4, 6} 2. I Microsoft Excel kan du beregne en modus ved at bruge funktionen af samme navn, MODE-funktionen. For vores eksempeldatasæt lyder formlen således:

=MODE(C2:C8)

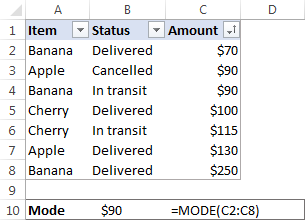
I situationer, hvor der er to eller flere tilstande i dit datasæt, vil Excel MODE-funktionen returnere den laveste tilstand .

Middelværdi vs. median: hvad er bedst?

Generelt er der ikke noget "bedste" mål for central tendens. Hvilket mål du skal bruge afhænger mest af den type data, du arbejder med, og af din forståelse af den "typiske værdi", du forsøger at estimere.

For en symmetrisk fordeling (hvor værdierne forekommer med regelmæssige frekvenser) er middelværdi, median og modus den samme. For en skæv distribution (hvor der er et lille antal ekstremt høje eller lave værdier), kan de tre mål for central tendens være forskellige.

Da middelværdien påvirkes kraftigt af skæve data og outliers (ikke-typiske værdier, der er signifikant forskellige fra resten af dataene), median er det foretrukne mål for den centrale tendens for en asymmetrisk fordeling .

Det er f.eks. almindeligt accepteret, at medianen er bedre end gennemsnittet til beregning af en typisk løn Den bedste måde at forstå dette på er ved hjælp af et eksempel. Se venligst nogle eksempler på lønninger for almindelige job:

• Elektriker - $20/time
• Sygeplejerske - $26/time
• Politibetjent - $47/time
• Salgschef - $54/time
• Produktionsingeniør - $63/time

Lad os nu beregne gennemsnittet (middelværdien): læg ovenstående tal sammen og divider med 5: (20+26+47+54+63)/5=42. Gennemsnitslønnen er altså 42 $/time. Medianlønnen er 47 $/time, og det er politibetjenten, der tjener den (1/2 løn er lavere, og 1/2 er højere). I dette tilfælde giver middelværdien og medianen samme tal.

Men lad os se, hvad der sker, hvis vi udvider listen over lønninger ved at inkludere en berømthed, der tjener f.eks. omkring 30 millioner dollars om året, hvilket svarer til ca. 14.500 dollars i timen. Nu bliver gennemsnitslønnen 2.451,67 dollars i timen, en løn, som ingen tjener! I modsætning hertil ændres medianen ikke væsentligt af denne ene outlier, den er 50,50 dollars i timen.

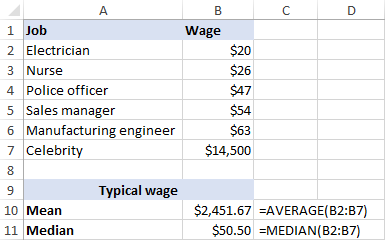
Enig, medianen giver et bedre billede af, hvad folk typisk tjener, fordi den ikke er så stærkt påvirket af unormale lønninger.

Sådan beregner du middelværdi, median og mode i Excel. Tak for din læsning og håber at se dig på vores blog i næste uge!