সংখ্যাগত তথ্য বিশ্লেষণ কৰাৰ সময়ত, আপুনি প্ৰায়ে "সাধাৰণ" মান পোৱাৰ কোনো উপায় বিচাৰিব পাৰে। ইয়াৰ বাবে, আপুনি তথাকথিত কেন্দ্ৰীয় প্ৰৱণতাৰ পৰিমাপসমূহ ব্যৱহাৰ কৰিব পাৰে যি এটা তথ্য গোটৰ ভিতৰত কেন্দ্ৰীয় অৱস্থান চিনাক্ত কৰা এটা মানক প্ৰতিনিধিত্ব কৰে বা, অধিক কাৰিকৰীভাৱে, এটা পৰিসংখ্যাগত বিতৰণত মধ্যম বা কেন্দ্ৰ। কেতিয়াবা, ইয়াক সাৰাংশ পৰিসংখ্যা হিচাপেও শ্ৰেণীভুক্ত কৰা হয়।

কেন্দ্ৰীয় প্ৰৱণতাৰ তিনিটা মূল পৰিমাপ হ'ল গড় , মধ্য আৰু ম'ড । এই সকলোবোৰ কেন্দ্ৰীয় অৱস্থানৰ বৈধ পৰিমাপ, কিন্তু প্ৰত্যেকেই এটা সাধাৰণ মানৰ বেলেগ বেলেগ ইংগিত দিয়ে, আৰু বিভিন্ন পৰিস্থিতিত কিছুমান পৰিমাপ আনতকৈ ব্যৱহাৰ কৰাটো অধিক উপযুক্ত।

গড় কেনেকৈ গণনা কৰিব লাগে Excel

ত গাণিতিক গড় , যাক গড় বুলিও কোৱা হয়, সম্ভৱতঃ আপুনি আটাইতকৈ পৰিচিত পৰিমাপ। গড় গণনা কৰা হয় সংখ্যাৰ এটা গোট যোগ কৰি আৰু তাৰ পিছত যোগফলটোক সেই সংখ্যাবোৰৰ গণনাৰে ভাগ কৰি।

উদাহৰণস্বৰূপে, সংখ্যাৰ গড় গণনা কৰিবলৈ {1, 2, 2, 3, 4, 6 }, আপুনি সেইবোৰ যোগ কৰে, আৰু তাৰ পিছত যোগফলটোক 6 ৰে ভাগ কৰে, যাৰ ফলত 3 পোৱা যায়: (1+2+2+3+4+6)/6=3।

মাইক্ৰ'ছফ্ট এক্সেলত, গড় হ'ব পাৰে নিম্নলিখিত ফাংচনসমূহৰ এটা ব্যৱহাৰ কৰি গণনা কৰা হ'ব:

• AVERAGE- সংখ্যাৰ গড় ঘূৰাই দিয়ে।
• AVERAGEA - যিকোনো তথ্যৰ সৈতে ঘৰৰ গড় ঘূৰাই দিয়ে (সংখ্যা, বুলিয়ান আৰু লিখনী মান ).
• AVERAGEIF - a ৰ ওপৰত ভিত্তি কৰি সংখ্যাৰ গড় বিচাৰি পায়একক মাপকাঠী।
• AVERAGEIFS - একাধিক মাপকাঠীৰ ওপৰত ভিত্তি কৰি সংখ্যাৰ গড় বিচাৰি পায়।

গভীৰ টিউটোৰিয়েলৰ বাবে, অনুগ্ৰহ কৰি ওপৰৰ লিংকসমূহ অনুসৰণ কৰক। এই ফলনসমূহে কেনেকৈ কাম কৰে তাৰ এটা ধাৰণাগত ধাৰণা পাবলৈ, নিম্নলিখিত উদাহৰণটো বিবেচনা কৰক।

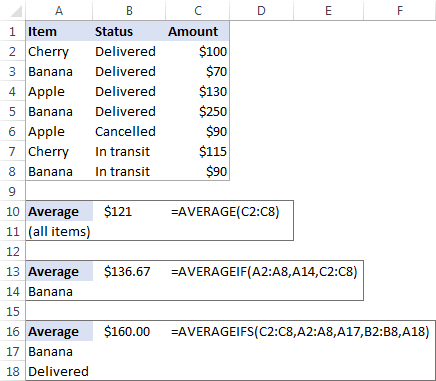
এটা বিক্ৰী প্ৰতিবেদনত (অনুগ্ৰহ কৰি তলৰ পৰ্দাশ্বট চাওক), ধৰি লওক আপুনি C2:C8 কোষসমূহত মানসমূহৰ গড় পাব বিচাৰে। ইয়াৰ বাবে এই সহজ সূত্ৰটো ব্যৱহাৰ কৰক:

=AVERAGE(C2:C8)

কেৱল "কল" বিক্ৰীৰ গড় পাবলৈ, এটা AVERAGEIF সূত্ৰ ব্যৱহাৰ কৰক:

=AVERAGEIF(A2:A8, "Banana", C2:C8)

২টা চৰ্তৰ ওপৰত ভিত্তি কৰি গড় গণনা কৰিবলৈ, ধৰক, "ডেলিভাৰড" অৱস্থাৰ সৈতে "কল" বিক্ৰীৰ গড়, AVERAGEIFS ব্যৱহাৰ কৰক:

=AVERAGEIFS(C2:C8,A2:A8, "Banana", B2:B8, "Delivered")

আপুনি আপোনাৰ চৰ্তসমূহ পৃথক কোষতও প্ৰৱেশ কৰিব পাৰে , আৰু আপোনাৰ সূত্ৰসমূহত থকা সেই কোষসমূহৰ উল্লেখ কৰক, এইদৰে:

এক্সেলত মধ্যমা কেনেকৈ বিচাৰিব

মধ্যম হৈছে মধ্যম মান সংখ্যাৰ এটা গোটত, যিবোৰ আৰোহী বা অৱনমিত ক্ৰমত সজোৱা হয়, অৰ্থাৎ আধা সংখ্যা মধ্যমাতকৈ ডাঙৰ আৰু আধা সংখ্যা মধ্যমাতকৈ কম। উদাহৰণস্বৰূপে, ডাটা ছেট {1, 2, 2, 3, 4, 6, 9} ৰ মধ্যমা 3।

এইটোৱে ভালদৰে কাম কৰে যেতিয়া এটা অদ্ভুত থাকে গোটত মানৰ সংখ্যা। কিন্তু যদি আপোনাৰ সম সংখ্যক মান থাকে তেন্তে কি হ’ব? এই ক্ষেত্ৰত মধ্যমা হ’ল মধ্যম মান দুটাৰ গাণিতিক গড় (গড়)। উদাহৰণস্বৰূপে, {১, ২, ২, ৩, ৪, ৬} ৰ মধ্যমা ২.৫। ইয়াক গণনা কৰিবলৈ আপুনি ৩য় আৰু ৪ৰ্থ মান লয়ডাটা ছেটত আৰু গড় হিচাপে ২.৫ ৰ মধ্যমা লাভ কৰিব পাৰি।

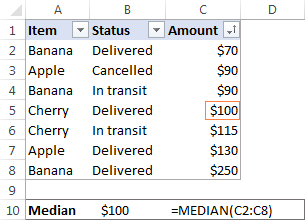
মাইক্ৰ'ছফ্ট এক্সেলত, MEDIAN ফাংচন ব্যৱহাৰ কৰি এটা মধ্যমা গণনা কৰা হয়। উদাহৰণস্বৰূপে, আমাৰ বিক্ৰী প্ৰতিবেদনত সকলো পৰিমাণৰ মধ্যমা পাবলৈ এই সূত্ৰটো ব্যৱহাৰ কৰক:

=MEDIAN(C2:C8)

উদাহৰণটো অধিক চিত্ৰকল্প কৰিবলৈ, মই C স্তম্ভত থকা সংখ্যাবোৰ আৰোহী ৰূপত সজাইছো ক্ৰম (যদিও এক্সেল মিডিয়ান সূত্ৰই কাম কৰিবলৈ প্ৰকৃততে ইয়াৰ প্ৰয়োজন নাই):

গড়ৰ বিপৰীতে, মাইক্ৰ'ছফ্ট এক্সেলে এটাৰ সৈতে মিডিয়ান গণনা কৰিবলৈ কোনো বিশেষ ফাংচন প্ৰদান নকৰে বা অধিক চৰ্ত। কিন্তু, আপুনি এই উদাহৰণসমূহত দেখুওৱাৰ দৰে দুটা বা অধিক ফলনৰ সংমিশ্ৰণ ব্যৱহাৰ কৰি MEDIANIF আৰু MEDIANIFS ৰ কাৰ্য্যকৰীতা "অনুকৰণ" কৰিব পাৰে:

• MEDIAN IF সূত্ৰ (এটা চৰ্তৰ সৈতে)
• MEDIAN IFS সূত্ৰ (একাধিক মাপকাঠীৰ সৈতে)

এক্সেলত মোড কেনেকৈ গণনা কৰিব

ম'ড হৈছে ডাটাছেটত সঘনাই দেখা দিয়া মান। গড় আৰু মধ্যমৰ বাবে কিছুমান গণনাৰ প্ৰয়োজন হ'লেও, এটা ধৰণ মান কেৱল প্ৰতিটো মান কিমানবাৰ ঘটে গণনা কৰি বিচাৰি পাব পাৰি।

উদাহৰণস্বৰূপে, মানসমূহৰ গোটৰ ধৰণ {1, 2, 2, 3 , 4, 6} হৈছে 2. মাইক্ৰ'ছফ্ট এক্সেলত, আপুনি একে নামৰ ফাংচন, MODE ফাংচন ব্যৱহাৰ কৰি এটা মোড গণনা কৰিব পাৰে। আমাৰ নমুনা ডাটা ছেটৰ বাবে, সূত্ৰটো তলত দিয়া ধৰণে যায়:

=MODE(C2:C8)

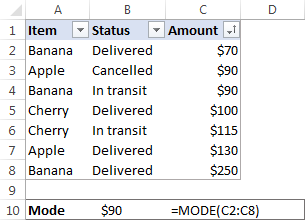
যেতিয়া আপোনাৰ ডাটা ছেটত দুটা বা তাতকৈ অধিক মোড থাকে, এক্সেল MODE ফাংচন সৰ্বনিম্ন ধৰণ ঘূৰাই দিব।

গড় বনাম মধ্যমা: কোনটো ভাল?

সাধাৰণতে, কেন্দ্ৰীয় প্ৰৱণতাৰ কোনো "শ্ৰেষ্ঠ" পৰিমাপ নাই। কোনটো পৰিমাপ ব্যৱহাৰ কৰিব লাগে সেইটো বেছিভাগেই আপুনি কাম কৰা তথ্যৰ ধৰণৰ ওপৰত নিৰ্ভৰ কৰে আৰু লগতে আপুনি অনুমান কৰিবলৈ চেষ্টা কৰা "সাধাৰণ মান"ৰ বিষয়ে আপোনাৰ বুজাবুজিৰ ওপৰত নিৰ্ভৰ কৰে।

এটা প্ৰতিসম বিতৰণৰ বাবে (in নিয়মিত কম্পাঙ্কত কোনবোৰ মান ঘটে), গড়, মধ্যমা আৰু ধৰণ একে। তিৰ্যক বিতৰণ ৰ বাবে (য'ত অতি উচ্চ বা কম মান কম সংখ্যক থাকে), কেন্দ্ৰীয় প্ৰৱণতাৰ তিনিটা পৰিমাপ বেলেগ হ'ব পাৰে।

যিহেতু গড় তিৰ্যক তথ্য আৰু আউটলাইয়াৰৰ দ্বাৰা বহু পৰিমাণে প্ৰভাৱিত হয় (অসাধাৰণ মান যি বাকী তথ্যৰ পৰা যথেষ্ট পৃথক), মধ্য হৈছে অসম বিতৰণ ৰ বাবে কেন্দ্ৰীয় প্ৰৱণতাৰ পছন্দৰ পৰিমাপ।

উদাহৰণস্বৰূপে, সাধাৰণতে মানি লোৱা হয় যে সাধাৰণ দৰমহা গণনাৰ বাবে গড়তকৈ মধ্যমা ভাল। কিয়? এই কথা বুজিবলৈ আটাইতকৈ উত্তম উপায় হ’ব এটা উদাহৰণৰ পৰা। অনুগ্ৰহ কৰি সাধাৰণ চাকৰিৰ বাবে কেইটামান নমুনা দৰমহা চাওক:

• ইলেক্ট্ৰিচিয়ান - $20/ঘণ্টা
• নাৰ্ছ - $26/ঘণ্টা
• পুলিচ বিষয়া - $47/ঘণ্টা
• বিক্ৰী পৰিচালক - $54/ঘণ্টা
• উৎপাদন অভিযন্তা - $63/ঘণ্টা

এতিয়া, গড় (গড়) গণনা কৰা যাওক: ওপৰৰ সংখ্যাবোৰ যোগ কৰি ভাগ কৰক ৫ ৰ দ্বাৰা: (২০+২৬+৪৭+৫৪+৬৩)/৫=৪২। গতিকে, গড় মজুৰি ৪২ ডলাৰ/ঘণ্টা। দ্য...মধ্যম মজুৰি ৪৭ ডলাৰ/ঘণ্টা, আৰু ইয়াক আৰক্ষী বিষয়াই উপাৰ্জন কৰে (১/২ মজুৰি কম, আৰু ১/২ বেছি)। বাৰু, এই বিশেষ ক্ষেত্ৰত গড় আৰু মধ্যমাই একে সংখ্যা দিয়ে।

কিন্তু চাওঁ আহক যদি আমি মজুৰিৰ তালিকাখন বৃদ্ধি কৰি এনে এজন চেলিব্ৰিটিক অন্তৰ্ভুক্ত কৰি বৃদ্ধি কৰোঁ যিয়ে, ধৰক, প্ৰায় ৩ কোটি ডলাৰ/বছৰ উপাৰ্জন কৰে, যিটো মোটামুটিভাৱে ১৪,৫০০ ডলাৰ/ঘণ্টা। এতিয়া গড় মজুৰি হয় ২,৪৫১.৬৭ ডলাৰ/ঘণ্টা, যিটো মজুৰি কোনেও উপাৰ্জন নকৰে! ইয়াৰ বিপৰীতে এই এটা আউটলাইয়াৰৰ দ্বাৰা মধ্যমা বিশেষ পৰিৱৰ্তন নহয়, ই $50.50/ঘণ্টা।

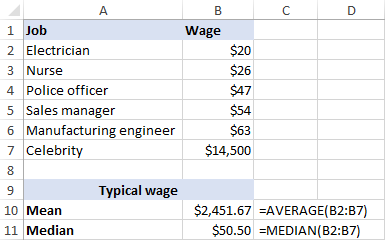
একমত, মধ্যমাটোৱে মানুহে সাধাৰণতে কি উপাৰ্জন কৰে তাৰ এটা ভাল ধাৰণা দিয়ে কাৰণ ই অস্বাভাৱিক দৰমহাৰ দ্বাৰা ইমান শক্তিশালীভাৱে প্ৰভাৱিত নহয়।

আপুনি Excel ত গড়, মধ্যমা আৰু ধৰণ গণনা কৰে। পঢ়াৰ বাবে ধন্যবাদ আৰু অহা সপ্তাহত আমাৰ ব্লগত লগ পাম বুলি আশা কৰিলোঁ!