เมื่อวิเคราะห์ข้อมูลตัวเลข คุณมักจะมองหาวิธีรับค่า "ทั่วไป" เพื่อจุดประสงค์นี้ คุณสามารถใช้สิ่งที่เรียกว่า มาตรวัดแนวโน้มเข้าสู่ส่วนกลาง ซึ่งแสดงถึงค่าเดียวที่ระบุตำแหน่งศูนย์กลางภายในชุดข้อมูล หรือในทางเทคนิคกว่านั้น ค่ากึ่งกลางหรือกึ่งกลางในการแจกแจงทางสถิติ บางครั้ง พวกเขายังถูกจัดประเภทเป็นสถิติสรุปอีกด้วย

การวัดแนวโน้มเข้าสู่ส่วนกลางหลักสามประการ ได้แก่ ค่าเฉลี่ย , ค่ามัธยฐาน และ โหมด ทั้งหมดนี้เป็นการวัดที่ถูกต้องของตำแหน่งศูนย์กลาง แต่แต่ละค่าบ่งชี้ค่าทั่วไปที่แตกต่างกัน และภายใต้สถานการณ์ที่แตกต่างกัน การวัดบางอย่างก็เหมาะสมกว่าที่จะใช้มากกว่าค่าอื่นๆ

วิธีคำนวณค่าเฉลี่ย ใน Excel

ค่าเฉลี่ยเลขคณิต หรือที่เรียกว่า ค่าเฉลี่ย น่าจะเป็นหน่วยวัดที่คุณคุ้นเคยมากที่สุด ค่าเฉลี่ยคำนวณโดยการบวกกลุ่มของตัวเลขแล้วหารผลรวมด้วยจำนวนตัวเลขเหล่านั้น

ตัวอย่างเช่น ในการคำนวณค่าเฉลี่ยของตัวเลข {1, 2, 2, 3, 4, 6 } คุณบวกกันแล้วหารผลรวมด้วย 6 ซึ่งได้ 3: (1+2+2+3+4+6)/6=3

ใน Microsoft Excel ค่าเฉลี่ยสามารถ คำนวณโดยใช้หนึ่งในฟังก์ชันต่อไปนี้:

• AVERAGE- ส่งกลับค่าเฉลี่ยของตัวเลข
• AVERAGEA - ส่งกลับค่าเฉลี่ยของเซลล์พร้อมข้อมูลใดๆ (ตัวเลข ค่าบูลีน และข้อความ ).
• AVERAGEIF - หาค่าเฉลี่ยของตัวเลขตาม aเกณฑ์เดียว
• AVERAGEIFS - ค้นหาค่าเฉลี่ยของตัวเลขตามเกณฑ์หลายเกณฑ์

สำหรับบทช่วยสอนเชิงลึก โปรดไปที่ลิงก์ด้านบน หากต้องการทราบแนวคิดเกี่ยวกับวิธีการทำงานของฟังก์ชันเหล่านี้ ให้พิจารณาตัวอย่างต่อไปนี้

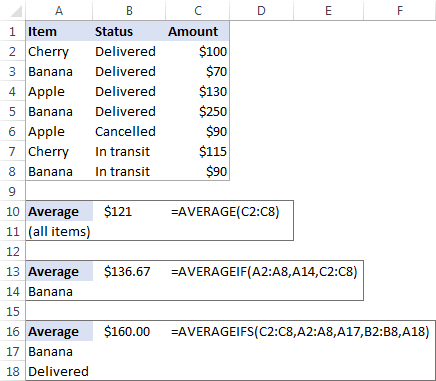
ในรายงานการขาย (โปรดดูภาพหน้าจอด้านล่าง) สมมติว่าคุณต้องการรับค่าเฉลี่ยของค่าในเซลล์ C2:C8 สำหรับสิ่งนี้ ใช้สูตรง่ายๆ นี้:

=AVERAGE(C2:C8)

หากต้องการหาค่าเฉลี่ยของยอดขาย "กล้วย" เท่านั้น ให้ใช้สูตร AVERAGEIF:

=AVERAGEIF(A2:A8, "Banana", C2:C8)

หากต้องการคำนวณค่าเฉลี่ยตามเงื่อนไข 2 ข้อ เช่น ค่าเฉลี่ยของยอดขาย "กล้วย" ที่มีสถานะ "ส่งแล้ว" ให้ใช้ AVERAGEIFS:

=AVERAGEIFS(C2:C8,A2:A8, "Banana", B2:B8, "Delivered")

คุณยังสามารถป้อนเงื่อนไขของคุณในเซลล์ที่แยกจากกัน และอ้างอิงเซลล์เหล่านั้นในสูตรของคุณ เช่น

วิธีหาค่ามัธยฐานใน Excel

ค่ามัธยฐาน คือค่ากลาง ในกลุ่มของตัวเลขซึ่งเรียงจากน้อยไปมากหรือมากไปน้อย เช่น ครึ่งหนึ่งของตัวเลขมากกว่าค่ามัธยฐาน และครึ่งหนึ่งของตัวเลขน้อยกว่าค่ามัธยฐาน ตัวอย่างเช่น ค่ามัธยฐานของชุดข้อมูล {1, 2, 2, 3, 4, 6, 9} คือ 3

วิธีนี้ใช้ได้ดีเมื่อมีเลขคี่ จำนวนค่าในกลุ่ม แต่ถ้าคุณมีค่า เลขคู่ ล่ะ ในกรณีนี้ ค่ามัธยฐานคือค่าเฉลี่ยเลขคณิต (ค่าเฉลี่ย) ของค่ากลางสองค่า ตัวอย่างเช่น ค่ามัธยฐานของ {1, 2, 2, 3, 4, 6} คือ 2.5 ในการคำนวณ คุณต้องใช้ค่าที่ 3 และ 4ในชุดข้อมูลและหาค่าเฉลี่ยเพื่อให้ได้ค่ามัธยฐานเท่ากับ 2.5

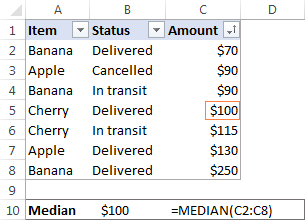
ใน Microsoft Excel ค่ามัธยฐานจะคำนวณโดยใช้ฟังก์ชัน MEDIAN ตัวอย่างเช่น หากต้องการทราบค่ามัธยฐานของจำนวนเงินทั้งหมดในรายงานการขายของเรา ให้ใช้สูตรนี้:

=MEDIAN(C2:C8)

เพื่อให้ตัวอย่างเห็นภาพมากขึ้น ฉันได้จัดเรียงตัวเลขในคอลัมน์ C จากน้อยไปหามาก ลำดับ (แม้ว่าจะไม่จำเป็นสำหรับสูตรค่ามัธยฐานของ Excel ในการทำงาน):

ตรงกันข้ามกับค่าเฉลี่ย Microsoft Excel ไม่มีฟังก์ชันพิเศษใดๆ ในการคำนวณค่ามัธยฐานด้วยค่ามัธยฐาน หรือเงื่อนไขอื่นๆ อย่างไรก็ตาม คุณสามารถ "จำลอง" การทำงานของ MEDIANIF และ MEDIANIFS ได้โดยใช้ฟังก์ชันตั้งแต่สองฟังก์ชันขึ้นไปตามที่แสดงในตัวอย่างต่อไปนี้:

• สูตร MEDIAN IF (โดยมีเงื่อนไขเดียว)
• สูตร MEDIAN IFS (มีหลายเกณฑ์)

วิธีการคำนวณโหมดใน Excel

โหมด คือค่าที่เกิดขึ้นบ่อยที่สุดในชุดข้อมูล ในขณะที่ค่าเฉลี่ยและค่ามัธยฐานจำเป็นต้องมีการคำนวณบางอย่าง ค่าโหมดสามารถหาได้ง่ายๆ โดยการนับจำนวนครั้งที่แต่ละค่าเกิดขึ้น

ตัวอย่างเช่น โหมดของชุดค่า {1, 2, 2, 3 , 4, 6} คือ 2 ใน Microsoft Excel คุณสามารถคำนวณโหมดได้โดยใช้ฟังก์ชันที่มีชื่อเดียวกัน นั่นคือฟังก์ชัน MODE สำหรับชุดข้อมูลตัวอย่างของเรา สูตรจะเป็นดังนี้:

=MODE(C2:C8)

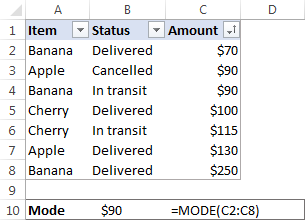
ในสถานการณ์ที่มีสองโหมดขึ้นไปในชุดข้อมูลของคุณ Excel ฟังก์ชันโหมดจะส่งคืน โหมดต่ำสุด .

ค่าเฉลี่ยเทียบกับค่ามัธยฐาน: แบบไหนดีกว่ากัน

โดยทั่วไปแล้ว ไม่มีการวัดแนวโน้มเข้าสู่ส่วนกลางที่ "ดีที่สุด" การวัดที่จะใช้ส่วนใหญ่ขึ้นอยู่กับประเภทของข้อมูลที่คุณกำลังทำงานด้วย เช่นเดียวกับความเข้าใจของคุณเกี่ยวกับ "ค่าทั่วไป" ที่คุณพยายามประมาณ

สำหรับ การกระจายแบบสมมาตร (ใน ค่าที่เกิดขึ้นที่ความถี่ปกติ) ค่าเฉลี่ย มัธยฐาน และฐานนิยมจะเหมือนกัน สำหรับการแจกแจง เบ้ (ซึ่งมีค่าสูงหรือต่ำมากจำนวนน้อย) การวัดแนวโน้มเข้าสู่ส่วนกลางทั้งสามแบบอาจแตกต่างกัน

เนื่องจากค่าเฉลี่ย ได้รับผลกระทบอย่างมากจากข้อมูลที่เบ้และค่าผิดปกติ (ค่าที่ไม่ใช่ค่าปกติซึ่งแตกต่างอย่างมากจากข้อมูลส่วนที่เหลือ) ค่ามัธยฐาน เป็นค่าวัดแนวโน้มเข้าสู่ส่วนกลางที่ต้องการสำหรับ การกระจายแบบอสมมาตร

ตัวอย่างเช่น เป็นที่ยอมรับโดยทั่วไปว่าค่ามัธยฐานดีกว่าค่าเฉลี่ยในการคำนวณ เงินเดือนทั่วไป ทำไม วิธีที่ดีที่สุดในการทำความเข้าใจสิ่งนี้คือจากตัวอย่าง โปรดดูตัวอย่างเงินเดือนบางส่วนสำหรับงานทั่วไป:

• ช่างไฟฟ้า - $20/ชั่วโมง
• พยาบาล - $26/ชั่วโมง
• เจ้าหน้าที่ตำรวจ - $47/ชั่วโมง
• ผู้จัดการฝ่ายขาย - $54/ชั่วโมง
• วิศวกรฝ่ายผลิต - $63/ชั่วโมง

ตอนนี้ มาคำนวณค่าเฉลี่ยกัน: บวกตัวเลขด้านบนแล้วหาร โดย 5: (20+26+47+54+63)/5=42 ดังนั้น ค่าจ้างเฉลี่ยคือ 42 เหรียญต่อชั่วโมง เดอะค่าจ้างเฉลี่ยอยู่ที่ 47 ดอลลาร์ต่อชั่วโมง และเจ้าหน้าที่ตำรวจเป็นผู้มีรายได้ (ค่าจ้าง 1/2 ต่ำกว่า และ 1/2 สูงกว่า) ในกรณีนี้ ค่าเฉลี่ยและค่ามัธยฐานให้ตัวเลขใกล้เคียงกัน

แต่มาดูกันว่าจะเกิดอะไรขึ้นหากเราขยายรายการค่าจ้างโดยรวมคนดังที่ทำรายได้ เช่น ประมาณ 30 ล้านเหรียญสหรัฐต่อปี ซึ่งก็คือประมาณ $14,500/ชม. ตอนนี้ค่าจ้างเฉลี่ยกลายเป็น 2,451.67 ดอลลาร์ต่อชั่วโมง ซึ่งเป็นค่าจ้างที่ไม่มีใครได้รับ! ในทางตรงกันข้าม ค่ามัธยฐานไม่ได้เปลี่ยนแปลงอย่างมีนัยสำคัญจากค่าผิดปกตินี้ แต่เป็น $50.50/ชั่วโมง

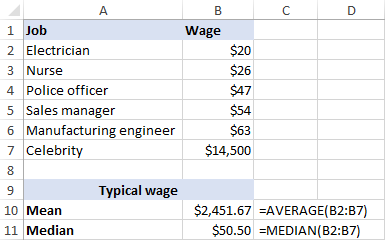
เห็นด้วย ค่ามัธยฐานให้แนวคิดที่ดีขึ้นเกี่ยวกับสิ่งที่ผู้คนมักได้รับเนื่องจากค่ามัธยฐาน ไม่ได้รับผลกระทบอย่างมากจากเงินเดือนที่ผิดปกติ

นี่คือวิธีที่คุณคำนวณค่าเฉลี่ย ค่ามัธยฐาน และโหมดใน Excel ฉันขอขอบคุณสำหรับการอ่านและหวังว่าจะได้พบคุณในบล็อกของเราในสัปดาห์หน้า!