संख्यात्मक डेटाचे विश्लेषण करताना, तुम्ही अनेकदा "नमुनेदार" मूल्य मिळविण्याचा काही मार्ग शोधत असाल. या उद्देशासाठी, तुम्ही तथाकथित केंद्रीय प्रवृत्तीचे उपाय वापरू शकता जे डेटा सेटमधील मध्यवर्ती स्थान किंवा अधिक तांत्रिकदृष्ट्या, सांख्यिकीय वितरणातील मध्य किंवा केंद्र ओळखणारे एकल मूल्य दर्शवतात. काहीवेळा, त्यांचे सारांश सांख्यिकी म्हणून वर्गीकरण देखील केले जाते.

मध्यवर्ती प्रवृत्तीचे तीन मुख्य उपाय आहेत मीन , मध्यम आणि मोड . ते सर्व मध्यवर्ती स्थानाचे वैध माप आहेत, परंतु प्रत्येक विशिष्ट मूल्याचे भिन्न संकेत देते आणि भिन्न परिस्थितींमध्ये काही उपाय इतरांपेक्षा वापरण्यास अधिक योग्य असतात.

मीनची गणना कशी करावी Excel मध्ये

अंकगणित मध्य , ज्याला सरासरी असेही संबोधले जाते, हे कदाचित तुम्हाला सर्वात परिचित असलेले माप आहे. संख्यांचा समूह जोडून आणि नंतर त्या संख्यांच्या मोजणीने बेरीज भागून सरासरीची गणना केली जाते.

उदाहरणार्थ, {1, 2, 2, 3, 4, 6 संख्यांची सरासरी काढण्यासाठी }, तुम्ही त्यांना जोडता, आणि नंतर बेरीज 6 ने विभाजित करा, ज्यामुळे 3 मिळते: (1+2+2+3+4+6)/6=3.

Microsoft Excel मध्ये, सरासरी खालीलपैकी एक फंक्शन वापरून गणना करा:

• AVERAGE- संख्यांची सरासरी मिळवते.
• AVERAGEA - कोणत्याही डेटासह सेलची सरासरी मिळवते (संख्या, बुलियन आणि मजकूर मूल्ये ).
• AVERAGEIF - a वर आधारित संख्यांची सरासरी शोधतेएकच निकष.
• AVERAGEIFS - एकाधिक निकषांवर आधारित संख्यांची सरासरी शोधते.

सखोल ट्यूटोरियलसाठी, कृपया वरील लिंक्सचे अनुसरण करा. ही फंक्शन्स कशी कार्य करतात याची वैचारिक कल्पना मिळविण्यासाठी, खालील उदाहरणाचा विचार करा.

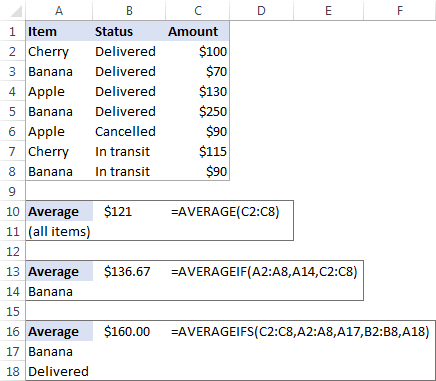
विक्री अहवालात (कृपया खाली स्क्रीनशॉट पहा), समजा तुम्हाला C2:C8 सेलमधील मूल्यांची सरासरी मिळवायची आहे. यासाठी, हा साधा फॉर्म्युला वापरा:

=AVERAGE(C2:C8)

फक्त "केळी" विक्रीची सरासरी मिळवण्यासाठी, AVERAGEIF सूत्र वापरा:

=AVERAGEIF(A2:A8, "Banana", C2:C8)

2 अटींवर आधारित सरासरी काढण्यासाठी, "वितरित" स्थितीसह "केळी" विक्रीची सरासरी काढण्यासाठी, AVERAGEIFS वापरा:

=AVERAGEIFS(C2:C8,A2:A8, "Banana", B2:B8, "Delivered")

तुम्ही तुमच्या अटी वेगळ्या सेलमध्ये देखील प्रविष्ट करू शकता. , आणि तुमच्या सूत्रांमध्ये त्या सेलचा संदर्भ द्या, जसे की:

एक्सेलमध्ये मध्यक कसे शोधायचे

मध्य हे मध्यम मूल्य आहे संख्यांच्या गटामध्ये, ज्या चढत्या किंवा उतरत्या क्रमाने मांडल्या जातात, म्हणजे अर्ध्या संख्या मध्यापेक्षा मोठ्या असतात आणि अर्ध्या संख्या मध्यकापेक्षा कमी असतात. उदाहरणार्थ, डेटा सेटचा मध्यक {1, 2, 2, 3, 4, 6, 9} आहे ​​3.

जेव्हा विषम असतात तेव्हा हे चांगले कार्य करते गटातील मूल्यांची संख्या. पण तुमच्याकडे मूल्यांची सम संख्या असल्यास काय? या प्रकरणात, मध्यक हा दोन मध्यम मूल्यांचा अंकगणितीय सरासरी (सरासरी) आहे. उदाहरणार्थ, {1, 2, 2, 3, 4, 6} चा मध्यक 2.5 आहे. त्याची गणना करण्यासाठी, तुम्ही 3री आणि 4 थी मूल्ये घ्याडेटा सेटमध्ये आणि 2.5 चा मध्यक मिळविण्यासाठी त्यांची सरासरी काढा.

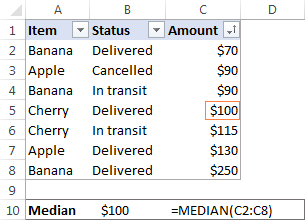
Microsoft Excel मध्ये, MEDIAN फंक्शन वापरून मेडियन काढला जातो. उदाहरणार्थ, आमच्या विक्री अहवालातील सर्व रकमेचा मध्य मिळवण्यासाठी, हे सूत्र वापरा:

=MEDIAN(C2:C8)

उदाहरणार्थ अधिक स्पष्टीकरण देण्यासाठी, मी स्तंभ C मधील संख्या चढत्या क्रमाने लावल्या आहेत. ऑर्डर (जरी प्रत्यक्षात एक्सेल मीडियन फॉर्म्युला कार्य करण्यासाठी आवश्यक नाही):

सरासरीच्या विरूद्ध, मायक्रोसॉफ्ट एक्सेल एकासह मध्यक मोजण्यासाठी कोणतेही विशेष कार्य प्रदान करत नाही किंवा अधिक अटी. तथापि, तुम्ही या उदाहरणांमध्ये दाखवल्याप्रमाणे दोन किंवा अधिक फंक्शन्सचे संयोजन वापरून MEDIANIF आणि MEDIANIFS च्या कार्यक्षमतेचे "अनुकरण" करू शकता:

• MEDIAN IF सूत्र (एका अटीसह)
• MEDIAN IFS फॉर्म्युला (एकाधिक निकषांसह)

एक्सेलमधील मोडची गणना कशी करायची

मोड हे डेटासेटमध्ये सर्वाधिक वारंवार आढळणारे मूल्य आहे. सरासरी आणि मध्यकाला काही गणना आवश्यक असताना, प्रत्येक मूल्य किती वेळा येते याची मोजणी करून मोड मूल्य शोधले जाऊ शकते.

उदाहरणार्थ, मूल्यांच्या सेटचा मोड {1, 2, 2, 3 , 4, 6} 2 आहे. मायक्रोसॉफ्ट एक्सेलमध्ये, तुम्ही त्याच नावाचे फंक्शन, MODE फंक्शन वापरून मोडची गणना करू शकता. आमच्या नमुना डेटा सेटसाठी, सूत्र खालीलप्रमाणे आहे:

=MODE(C2:C8)

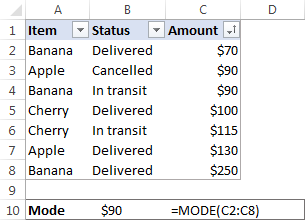
जेव्हा तुमच्या डेटा सेटमध्ये दोन किंवा अधिक मोड असतात अशा परिस्थितीत, Excel MODE कार्य सर्वोत्तम मोड परत करेल.

मध्य वि. मध्य: कोणते चांगले आहे?

सामान्यत:, मध्यवर्ती प्रवृत्तीचे कोणतेही "सर्वोत्तम" माप नाही. कोणते माप वापरायचे हे मुख्यतः तुम्ही काम करत असलेल्या डेटाच्या प्रकारावर तसेच तुम्ही अंदाज लावण्याचा प्रयत्न करत असलेल्या "नमुनेदार मूल्य" बद्दलच्या तुमच्या समजावर अवलंबून आहे.

सममितीय वितरणासाठी (मध्ये कोणती मूल्ये नियमित फ्रिक्वेन्सीवर आढळतात), मध्य, मध्य आणि मोड समान आहेत. तिरकस वितरण (जेथे अत्यंत उच्च किंवा कमी मूल्ये कमी आहेत) साठी, मध्यवर्ती प्रवृत्तीचे तीन उपाय भिन्न असू शकतात.

मध्य स्क्युड डेटा आणि आउटलियर्स (नॉन-टीपिकल मूल्ये जी उर्वरित डेटापेक्षा लक्षणीय भिन्न आहेत) द्वारे मोठ्या प्रमाणावर प्रभावित होतात, मध्य हे असममितीय वितरण साठी मध्यवर्ती प्रवृत्तीचे पसंतीचे माप आहे.

उदाहरणार्थ, हे सामान्यतः मान्य केले जाते की सामान्य पगार मोजण्यासाठी मध्यक सरासरीपेक्षा चांगला आहे. का? हे समजून घेण्याचा सर्वोत्तम मार्ग उदाहरणावरून असेल. कृपया सामान्य नोकऱ्यांसाठी काही नमुना पगार पहा:

• इलेक्ट्रिशियन - $20/तास
• नर्स - $26/तास
• पोलीस अधिकारी - $47/तास
• विक्री व्यवस्थापक - $54/तास
• उत्पादन अभियंता - $63/तास

आता, सरासरी काढूया (म्हणजे): वरील संख्या जोडा आणि विभाजित करा ५ द्वारे: (२०+२६+४७+५४+६३)/५=४२. तर, सरासरी वेतन $42/तास आहे. दसरासरी वेतन $47/तास आहे, आणि ते कमावणारे पोलिस अधिकारी आहेत (1/2 वेतन कमी आहे, आणि 1/2 जास्त आहेत). बरं, या विशिष्ट प्रकरणात मध्य आणि मध्यक समान संख्या देतात.

परंतु, अंदाजे $30 दशलक्ष/वर्ष कमावणार्‍या सेलिब्रिटीचा समावेश करून आपण वेतनाची यादी वाढवल्यास काय होते ते पाहू या. $14,500/तास. आता, सरासरी वेतन $2,451.67/तास झाले आहे, असे वेतन जे कोणीही कमावत नाही! याउलट, या एका आउटलायरद्वारे मध्यक लक्षणीयरित्या बदललेले नाही, ते $५०.५०/तास आहे.

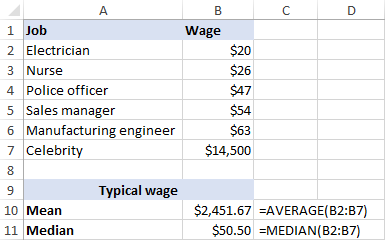
सहमत आहे, मध्यक लोक सामान्यतः काय कमावतात याची चांगली कल्पना देते कारण ते असामान्य पगाराचा इतका जोरदार परिणाम होत नाही.

तुम्ही एक्सेलमध्ये सरासरी, मध्य आणि मोड अशा प्रकारे मोजता. वाचल्याबद्दल मी तुमचा आभारी आहे आणि तुम्हाला पुढील आठवड्यात आमच्या ब्लॉगवर भेटण्याची आशा आहे!