Denne opplæringen forklarer syntaksen til Excel IRR-funksjonen og viser hvordan du bruker en IRR-formel for å beregne internrenten for en serie med årlige eller månedlige kontantstrømmer.

IRR i Excel er en av de økonomiske funksjonene for å beregne internrenten, som ofte brukes i kapitalbudsjettering for å bedømme forventet avkastning på investeringer.

IRR-funksjon i Excel

Excel IRR-funksjonen returnerer internrenten for en serie periodiske kontantstrømmer representert ved positive og negative tall.

I alle beregninger antas det implisitt at:

• Det er like tidsintervaller mellom alle kontantstrømmer.
• Alle kontantstrømmer skjer ved slutten av en periode .
• Fortjeneste generert av prosjekter reinvesteres til internrenten.

Funksjonen er tilgjengelig i alle versjoner av Excel for Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010 og Excel 2007.

Syntaksen til Exce l IRR-funksjonen er som følger:

Hvor:

• Verdier (påkrevd) – en matrise eller en referanse til en celleområde som representerer rekken av kontantstrømmer som du ønsker å finne internrenten for.
• Gjett (valgfritt) – din gjetning på hva internrenten kan være. Det skal angis som en prosentandel eller tilsvarende desimaltall. Hvisforventet, sjekk gjetteverdien – i tilfelle IRR-ligningen kan løses med flere rateverdier, returneres raten nærmest gjettet.

  

  Se også: Lag og formater tabeller i Outlook e-postmaler

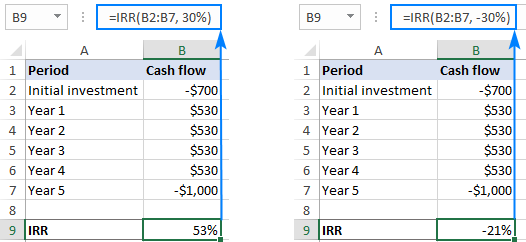
  Mulige løsninger:

  • Forutsatt at du vet hva slags avkastning du forventer fra en bestemt investering, bruk forventningen din som en gjetning.
  • Når du får mer enn én IRR for samme kontantstrøm, velger du en som er nærmest bedriftens kapitalkostnad som den "sanne" IRR.
  • Bruk MIRR-funksjonen for å unngå problemet med flere IRR.

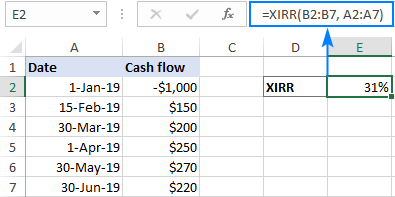
  Uregelmessige kontantstrømintervaller

  IRR-funksjonen i Excel er designet for å fungere med vanlige kontantstrømperioder som ukentlig, månedlig, kvartalsvis eller årlig. Hvis inn- og utstrømningene dine skjer med ulikt intervall, vil IRR fortsatt vurdere intervallene like og gi et feil resultat. I dette tilfellet, bruk XIRR-funksjonen i stedet for IRR.

  

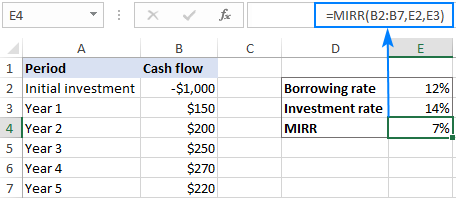
  Ulike låne- og reinvesteringssatser

  IRR-funksjonen innebærer at prosjektets inntjening (positive kontantstrømmer) ) reinvesteres kontinuerlig til internrenten. Men i det virkelige ordet er det ofte forskjellig hvor mye du låner penger og hvor mye du reinvesterer overskuddet. Heldigvis for oss har Microsoft Excel en spesiell funksjon for å ta seg av dette scenariet – MIRR-funksjonen.

  

  Slik gjør man IRR i Excel. For å se nærmere på eksemplene som er omtalt i detteveiledning, er du velkommen til å laste ned vår eksempelarbeidsbok til Bruke IRR-funksjonen i Excel. Jeg takker for at du leser og håper å se deg på bloggen vår neste uke!

  utelatt, brukes standardverdien på 0,1 (10 %).

For å beregne IRR for kontantstrømmer i B2:B5, bruker du for eksempel denne formelen:

=IRR(B2:B5)

For at resultatet skal vises riktig, sørg for at formatet Prosent er angitt for formelcellen (vanligvis gjør Excel dette automatisk).

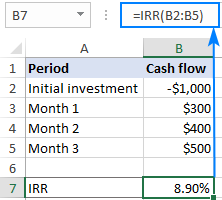
Som vist i skjermbildet ovenfor, gir vår Excel IRR-formel 8,9 %. Er denne prisen god eller dårlig? Vel, det avhenger av flere faktorer.

Generelt sammenlignes en beregnet internrente med et selskaps veide gjennomsnittlige kapitalkostnad eller hekksats . Hvis IRR er høyere enn hinderraten, anses prosjektet som en god investering; hvis lavere, bør prosjektet avvises.

I vårt eksempel, hvis det koster deg 7 % å låne penger, så er en IRR på ca. 9 % ganske bra. Men hvis kostnaden for midler er, for eksempel 12 %, så er IRR på 9 % ikke god nok.

I virkeligheten er det mange andre faktorer som påvirker en investeringsbeslutning, for eksempel netto nåverdi, absolutt returverdi osv. For mer informasjon, se IRR grunnleggende.

5 ting du bør vite om Excel IRR-funksjon

For å sikre at IRR-beregningen din i Excel er riktig utført, husk disse enkle fakta:

1. Argumentet verdier må inneholde minst én positiv verdi (som representerer inntekt) og én negativ verdi (som representererutlegg).
2. Kun tall i argumentet verdier blir behandlet; tekst, logiske verdier eller tomme celler ignoreres.
3. Kontantstrømmene trenger ikke nødvendigvis å være jevne, men de må skje med regelmessige intervaller , for eksempel månedlig, kvartalsvis eller årlig.
4. Fordi IRR i Excel tolker rekkefølgen av kontantstrømmer basert på rekkefølgen av verdier, bør verdiene være i kronologisk rekkefølge .
5. I de fleste situasjoner er gjett argument er egentlig ikke nødvendig. Imidlertid, hvis IRR-ligningen har mer enn én løsning, returneres raten nærmest gjetningen. Så formelen din gir et uventet resultat eller et #NUM! feil, prøv en annen gjetning.

Forstå IRR-formelen i Excel

Siden internrenten (IRR) er en diskonteringsrente som gjør netto nåverdi (NPV) av en gitt serie kontantstrømmer lik null, IRR-beregningen er avhengig av den tradisjonelle NPV-formelen:

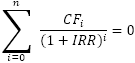
Hvor:

• CF - kontantstrøm
• i - periodenummer
• n - perioder totalt
• IRR - internrente

På grunn av en spesifikk karakter av denne formelen, er det ingen måte å beregne IRR på annet enn gjennom prøving og feiling. Microsoft Excel er også avhengig av denne teknikken, men utfører flere iterasjoner ekstremt raskt. Starter med gjetning (hvis levert) eller standard 10 %, går Excel IRR-funksjonen gjennomberegning til den finner resultatet nøyaktig innenfor 0,00001 %. Hvis et nøyaktig resultat ikke blir funnet etter 20 iterasjoner, vil #NUM! feilen returneres.

For å se hvordan det fungerer i praksis, la oss utføre denne IRR-beregningen på et eksempeldatasett. For det første vil vi prøve å gjette hva den interne avkastningen kan være (si 7%), og deretter regne ut netto nåverdi.

Forutsatt at B3 er kontantstrømmen og A3 er periodenummeret, følgende formel gir oss nåverdien (PV) av den fremtidige kontantstrømmen:

=B3/(1+7%)^A3

Deretter kopierer vi formelen ovenfor til andre celler og legger sammen alle nåverdiene, inkludert den initiale investering:

=SUM(C2:C5)

Og finn ut at ved 7 % får vi NPV på 37,90 USD:

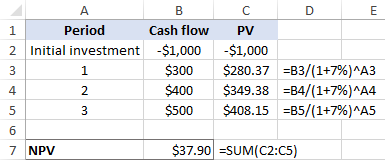
Tydeligvis er vår gjetning feil . La oss nå gjøre den samme beregningen basert på hastigheten beregnet av IRR-funksjonen (rundt 8,9%). Jepp, det fører til en null NPV:

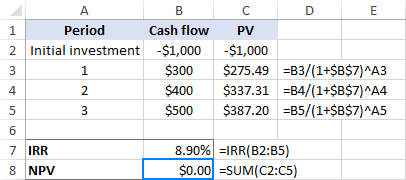
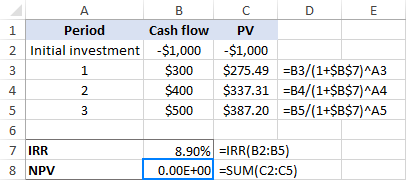
Tips. For å vise den nøyaktige NPV-verdien, velg å vise flere desimaler eller bruk Scientific-formatet. I dette eksemplet er NPV nøyaktig null, noe som er et svært sjeldent tilfelle!

Bruke IRR-funksjonen i Excel – formeleksempler

Nå som du vet det teoretiske grunnlaget av IRR-beregning i Excel, la oss lage et par formler for å se hvordan det fungerer i praksis.

Eksempel 1. Beregn IRR for månedlige kontantstrømmer

Forutsatt at du har drevet virksomhet i seks måneder og nå duønsker å finne ut avkastningen for kontantstrømmen din.

Å finne IRR i Excel er veldig enkelt:

1. Skriv inn startinvesteringen i en celle ( B2 i vårt tilfelle). Siden det er en utgående betaling, må den være et negativt tall.
2. Skriv inn de påfølgende kontantstrømmene i cellene under eller til høyre for den opprinnelige investeringen (B2:B8 i dette eksemplet ). Disse pengene har kommet inn gjennom salg, så vi legger inn disse som positive tall.

Nå er du klar til å beregne IRR for prosjektet:

=IRR(B2:B8)

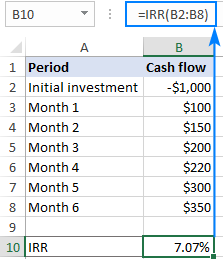
Merk. Ved månedlige kontantstrømmer gir IRR-funksjonen en månedlig avkastning. For å få en årlig avkastning for månedlig kontantstrøm kan du bruke XIRR-funksjonen.

Eksempel 2: Bruk gjetning i Excel IRR-formel

Du kan eventuelt angi en forventet internrente, for eksempel 10 prosent, i gjett -argumentet:

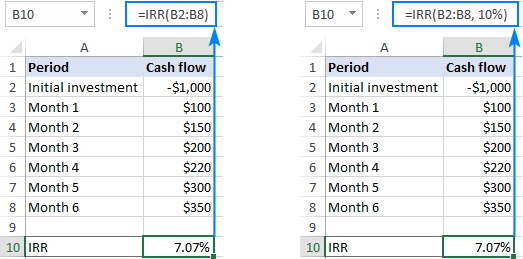
=IRR(B2:B8, 10%)

Som vist i skjermbildet nedenfor, har ikke vår gjetning noen innvirkning på resultatet. Men i noen tilfeller kan endring av gjetteverdien føre til at en IRR-formel returnerer en annen rate. For mer informasjon, se Flere IRR.

Eksempel 3. Finn IRR for å sammenligne investeringer

I kapitalbudsjettering brukes ofte IRR-verdier for å sammenligne investeringer og rangere prosjekter i forhold til potensiell lønnsomhet. Dette eksemplet demonstrerer teknikken i sinenkleste formen.

Forutsatt at du har tre investeringsalternativer og du bestemmer deg for hvilken du skal velge. Den rimelig anslåtte avkastningen på investeringene kan hjelpe deg med å ta en informert beslutning. For dette, skriv inn kontantstrømmen for hvert prosjekt i en egen kolonne, og beregn deretter internrenten for hvert prosjekt individuelt:

Formel for prosjekt 1:

=IRR(B2:B7)

Formel for prosjekt 2:

=IRR(C2:C7)

Formel for prosjekt 3:

=IRR(D2:D7)

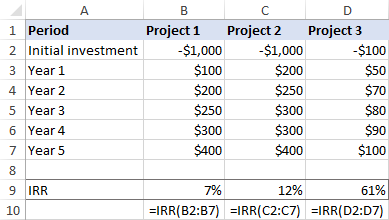
Gi at selskapets avkastningskrav er, for eksempel 9 %, prosjekt 1 bør avvises fordi dens IRR bare er 7 %.

De to andre investeringene er akseptable fordi begge kan generere en IRR høyere enn selskapets hinderrate. Hvilken ville du valgt?

Ved første øyekast ser prosjekt 3 mer foretrukket ut fordi det har den høyeste internrenten. Imidlertid er dens årlige kontantstrømmer mye lavere enn for prosjekt 2. I situasjoner der en liten investering har en svært høy avkastning, velger bedrifter ofte en investering med lavere prosentvis avkastning, men høyere absolutt (dollar) avkastningsverdi, som er prosjekt 2.

Konklusjonen er: investeringen med høyest internrente foretrekkes vanligvis, men for å få best mulig bruk av midlene dine bør du vurdere andre indikatorer også.

Eksempel 4 Beregn sammensatt årlig vekstrate (CAGR)

Selv om IRR-funksjonen i Excel erdesignet for å beregne den interne avkastningsraten, kan den også brukes til å beregne den sammensatte vekstraten. Du må bare omorganisere de opprinnelige dataene dine på denne måten:

• Behold den første verdien av den opprinnelige investeringen som et negativt tall og sluttverdien som et positivt tall.
• Bytt ut de midlertidige kontantstrømverdiene med nuller.

Når du er ferdig, skriv en vanlig IRR-formel, og den vil returnere CAGR:

=IRR(B2:B8)

For å være sikker på resultatet er riktig, kan du bekrefte det med den ofte brukte formelen for beregning av CAGR:

(end_value/start_value)^(1/antall perioder) -

Som vist i skjermbildet nedenfor, begge formlene gir samme resultat:

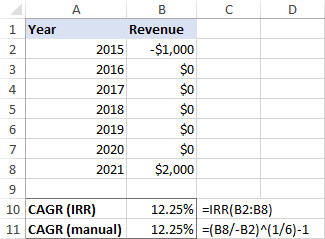
For mer informasjon, se Hvordan beregne CAGR i Excel.

IRR og NPV i Excel

Internrenten og netto nåverdi er to nært beslektede konsepter, og det er umulig å forstå IRR fullt ut uten å forstå NPV. Resultatet av IRR er ikke noe annet enn diskonteringsrenten som tilsvarer en null netto nåverdi.

Den vesentlige forskjellen er at NPV er et absolutt mål som reflekterer dollarbeløpet av verdi som kan oppnås eller tapes ved å foreta et prosjekt, mens IRR er den prosentvise avkastningen som forventes fra en investering.

På grunn av deres forskjellige natur kan IRR og NPV "konflikt" med hverandre - ett prosjekt kan ha en høyere NPVog den andre en høyere IRR. Når en slik konflikt oppstår, anbefaler finanseksperter å favorisere prosjektet med en høyere netto nåverdi.

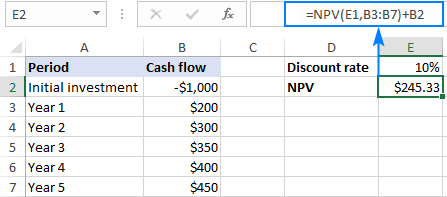
For bedre å forstå forholdet mellom IRR og NPV, vennligst vurder følgende eksempel. La oss si at du har et prosjekt som krever en initial investering på $1000 (celle B2) og en diskonteringsrente på 10 % (celle E1). Prosjektets levetid er fem år og forventet kontantstrøm for hvert år er oppført i celle B3:B7.

For å finne ut hvor mye de fremtidige kontantstrømmene er verdt nå, må vi beregne netto nåverdi av prosjektet. For dette, bruk NPV-funksjonen og trekk den opprinnelige investeringen fra den (fordi den opprinnelige investeringen er et negativt tall, brukes addisjonsoperasjonen):

=NPV(E1,B3:B7)+B2

En positiv netto nåverdi indikerer at prosjektet vårt kommer til å være lønnsomt:

Hvilken diskonteringsrente vil gjøre NPV lik null? Følgende IRR-formel gir svaret:

=IRR(B2:B7)

For å sjekke dette, ta NPV-formelen ovenfor og erstatt diskonteringsrenten (E1) med IRR (E4):

=NPV(E4,B3:B7)+B2

Eller du kan bygge inn IRR-funksjonen direkte i rate -argumentet til NPV:

=NPV(IRR(B2:B7),B3:B7)+B2

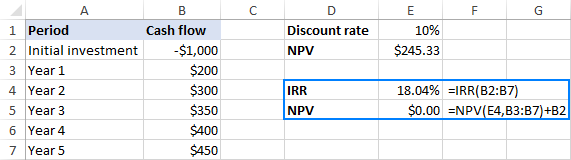
Skjermbildet ovenfor viser at NPV-verdien avrundet til 2 desimaler faktisk er lik null. Hvis du er nysgjerrig på å vite det nøyaktige tallet, sett Scientific-formatet til NPV-cellen eller velg å vise merdesimaler:

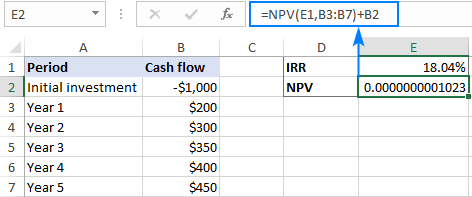
Som du kan se, er resultatet godt innenfor den deklarerte nøyaktigheten på 0,00001 prosent, og vi kan si at NPV faktisk er 0.

Tips. Hvis du ikke helt stoler på resultatet av IRR-beregningen i Excel, kan du alltid sjekke det ved å bruke NPV-funksjonen som vist ovenfor.

Excel IRR-funksjonen fungerer ikke

Hvis du har hatt problemer med IRR i Excel, kan følgende tips gi deg en pekepinn på hvordan du kan fikse det.

IRR-formelen returnerer #NUM ! feil

ET #NUM! feil kan returneres på grunn av disse årsakene:

• IRR-funksjonen finner ikke resultatet med opptil 0,000001 % nøyaktighet på 20. forsøk.
• De oppgitte verdiene -området inneholder ikke minst én negativ og minst én positiv kontantstrøm.

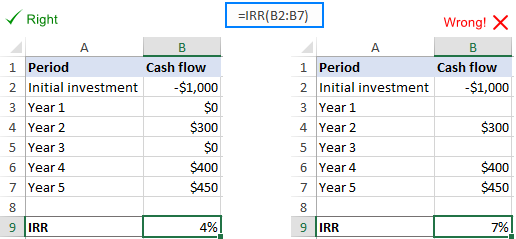
Blanke celler i verdimatrisen

I tilfelle ingen kontantstrøm oppstår i én eller flere perioder , kan du ende opp med tomme celler i området verdier . Og det er kilden til problemer fordi rader med tomme celler er utelatt fra Excel IRR-beregning. For å fikse dette, skriv bare inn nullverdier i alle tomme celler. Excel vil nå se de riktige tidsintervallene og beregne den interne avkastningen korrekt.

Flere IRR

I situasjoner når en kontantstrømserie endres fra negativ til positiv eller omvendt mer enn én gang, kan flere IRR-er bli funnet.

Hvis resultatet av formelen din er langt fra det du