Šioje pamokoje paaiškinama "Excel" funkcijos IRR sintaksė ir parodoma, kaip naudoti IRR formulę metinių arba mėnesinių pinigų srautų vidinei grąžos normai apskaičiuoti.

IRR programoje "Excel" yra viena iš finansinių funkcijų, skirtų vidinei grąžos normai apskaičiuoti, kuri dažnai naudojama sudarant kapitalo biudžetą, siekiant įvertinti numatomą investicijų grąžą.

IRR funkcija programoje "Excel

"Excel" IRR funkcija grąžina vidinę grąžos normą periodinių pinigų srautų, išreikštų teigiamais ir neigiamais skaičiais, serijai.

Visuose skaičiavimuose netiesiogiai daroma prielaida, kad:

• Yra vienodi laiko intervalai tarp visų pinigų srautų.
• Visi pinigų srautai atsiranda laikotarpio pabaiga .
• Projekto metu gautas pelnas yra reinvestuota pagal vidinę grąžos normą.

Ši funkcija yra visose "Office 365", "Excel 2019", "Excel 2019", "Excel 2016", "Excel 2013", "Excel 2010" ir "Excel 2007" versijose.

"Excel" IRR funkcijos sintaksė yra tokia:

Kur:

• Vertybės (privaloma) - masyvas arba nuoroda į langelių, vaizduojančių pinigų srautų, kuriems norite nustatyti vidinę grąžos normą, seriją, intervalą.
• Atspėkite (neprivaloma) - jūsų spėjimas, kokia galėtų būti vidinė grąžos norma. Ji turėtų būti nurodyta procentais arba atitinkamu dešimtainiuoju skaičiumi. Jei nepateikiama, naudojama numatytoji reikšmė 0,1 (10 %).

Pavyzdžiui, norėdami apskaičiuoti IRR pinigų srautams B2:B5, naudokite šią formulę:

=IRR(B2:B5)

Kad rezultatas būtų rodomas teisingai, įsitikinkite, kad Procentinė dalis nustatytas formulės ląstelės formatas (paprastai "Excel" tai daro automatiškai).

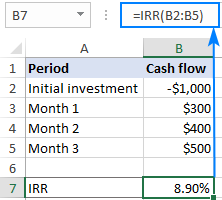
Kaip parodyta pirmiau pateiktoje ekrano nuotraukoje, mūsų "Excel" IRR formulė grąžina 8,9 %. Ar šis rodiklis yra geras, ar blogas? Na, tai priklauso nuo kelių veiksnių.

Paprastai apskaičiuota vidinė grąžos norma lyginama su įmonės vidutinė svertinė kapitalo kaina arba ribinė norma Jei IRR yra didesnė už ribinę normą, projektas laikomas gera investicija; jei mažesnė, projektas turėtų būti atmestas.

Mūsų pavyzdyje, jei pasiskolinti pinigų kainuoja 7 %, tuomet maždaug 9 % vidinė grąžos norma yra gana gera. Tačiau jei lėšų kaina yra, tarkime, 12 %, tuomet 9 % vidinė grąžos norma nėra pakankamai gera.

Iš tikrųjų yra daug kitų veiksnių, darančių įtaką investiciniam sprendimui, pavyzdžiui, grynoji dabartinė vertė, absoliučios grąžos vertė ir t. t. Daugiau informacijos rasite IRR pagrindai.

5 dalykai, kuriuos turėtumėte žinoti apie "Excel" IRR funkciją

Norėdami užtikrinti, kad IRR skaičiavimas "Excel" programoje būtų atliktas teisingai, prisiminkite šiuos paprastus faktus:

1. Svetainė reikšmės argumente turi būti bent vienas teigiamas vertė (rodanti pajamas) ir viena neigiamas vertę (kuri atspindi išlaidas).
2. Tik numeriai į reikšmės argumentas apdorojamas; tekstas, loginės reikšmės arba tušti langeliai ignoruojami.
3. Pinigų srautai nebūtinai turi būti tolygūs, tačiau jie turi atsirasti reguliarūs intervalai , pavyzdžiui, kas mėnesį, ketvirtį ar metus.
4. Kadangi "Excel" programa IRR interpretuoja pinigų srautų eiliškumą pagal verčių eiliškumą, vertės turėtų būti chronologine tvarka .
5. Daugeliu atvejų atspėti Tačiau jei IRR lygtis turi daugiau nei vieną sprendinį, grąžinama spėjimui artimiausia norma. Taigi, jei jūsų formulė duoda netikėtą rezultatą arba #NUM! klaidą, pabandykite kitą spėjimą.

IRR formulės supratimas programoje "Excel

Kadangi vidinė grąžos norma (IRR) yra diskonto norma, dėl kurios tam tikros pinigų srautų serijos grynoji dabartinė vertė (NPV) yra lygi nuliui, IRR skaičiavimas remiasi tradicine NPV formule:

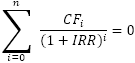
Kur:

• CF - pinigų srautas
• i - laikotarpio numeris
• n - iš viso laikotarpių
• IRR - vidinė grąžos norma

Dėl specifinės šios formulės prigimties nėra kito būdo apskaičiuoti IRR, kaip tik bandymų ir klaidų būdu. "Microsoft Excel" taip pat remiasi šiuo metodu, tačiau labai greitai atlieka kelias iteracijas. Pradėdama nuo spėjimo (jei pateiktas) arba numatytojo 10 %, "Excel" IRR funkcija atlieka skaičiavimus tol, kol nustato, kad rezultatas tikslus 0,00001 % tikslumu. Jei po 20 iteracijųtikslaus rezultato nerasta, grąžinama #NUM! klaida.

Kad pamatytume, kaip tai veikia praktiškai, atlikime šį vidinės grąžos normos skaičiavimą su pavyzdiniu duomenų rinkiniu. Pirmiausia pabandysime atspėti, kokia gali būti vidinė grąžos norma (tarkime, 7 %), ir tada apskaičiuosime grynąją dabartinę vertę.

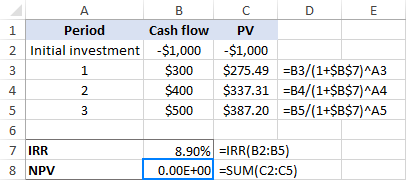
Darant prielaidą, kad B3 yra pinigų srautas, o A3 - laikotarpio numeris, pagal šią formulę gauname būsimo pinigų srauto dabartinę vertę (PV):

=B3/(1+7%)^A3

Tada nukopijuojame pirmiau pateiktą formulę į kitus langelius ir sudedame visas dabartines vertes, įskaitant pradinę investiciją:

=SUMA(C2:C5)

Ir sužinokite, kad, esant 7 %, gauname 37,90 USD grynąją dabartinę vertę:

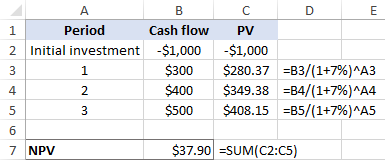
Akivaizdu, kad mūsų spėjimas yra klaidingas. Dabar atlikime tą patį skaičiavimą pagal IRR funkcijos apskaičiuotą normą (apie 8,9 %). Taip, ji iš tiesų duoda nulinę NPV:

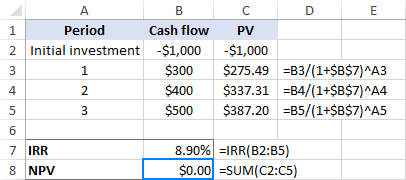
Patarimas. Norėdami parodyti tikslią grynosios grynosios vertės vertę, pasirinkite rodyti daugiau skaičių po kablelio arba taikyti mokslinį formatą. Šiame pavyzdyje grynoji grynoji grynoji vertė yra lygiai nulis, o tai labai retas atvejis!

IRR funkcijos naudojimas "Excel" programoje - formulės pavyzdžiai

Dabar, kai žinote teorinį IRR skaičiavimo "Excel" programoje pagrindą, sukurkime keletą formulių, kad pamatytumėte, kaip tai veikia praktiškai.

1 pavyzdys. Apskaičiuokite IRR mėnesiniams pinigų srautams

Tarkime, kad verslą vykdote šešis mėnesius ir dabar norite išsiaiškinti savo pinigų srautų grąžos normą.

Rasti IRR programoje "Excel" labai paprasta:

1. Įveskite pradinė investicija į tam tikrą langelį (mūsų atveju B2). Kadangi tai yra išeinantis mokėjimas, jis turi būti neigiamas skaičius.
2. Vėlesnius pinigų srautus įrašykite į langelius po pradine investicija arba į dešinę nuo jos (šiame pavyzdyje B2:B8). Šie pinigai buvo gaunami per pardavimus, todėl juos įrašome kaip teigiamas numeriai.

Dabar galite apskaičiuoti projekto IRR:

=IRR(B2:B8)

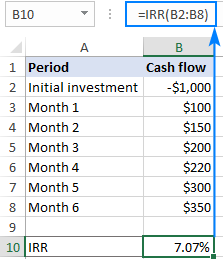
Pastaba. Jei pinigų srautai yra mėnesiniai, IRR funkcija duoda kas mėnesį Norint gauti metinę mėnesio pinigų srauto grąžos normą, galima naudoti XIRR funkciją.

2 pavyzdys: "Excel" IRR formulėje naudokite spėjimą

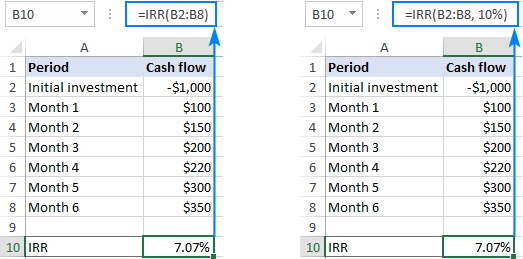
Pasirinktinai galite įrašyti tikėtiną vidinę grąžos normą, pvz., 10 proc. atspėti argumentas:

=IRR(B2:B8, 10%)

Kaip parodyta toliau pateiktoje ekrano nuotraukoje, mūsų spėjimas neturi jokios įtakos rezultatui. Tačiau kai kuriais atvejais, pakeitus spėjimo vertę, IRR formulė gali duoti kitokią normą. Daugiau informacijos rasite skyriuje Kelios IRR.

3 pavyzdys. Nustatykite IRR investicijoms palyginti

Sudarant kapitalo biudžetą, IRR vertės dažnai naudojamos investicijoms palyginti ir projektams reitinguoti pagal jų galimą pelningumą. Šiame pavyzdyje šis metodas demonstruojamas paprasčiausia forma.

Tarkime, kad turite tris investavimo galimybes ir sprendžiate, kurią iš jų pasirinkti. Pagrįstai prognozuojama investicijų grąža gali padėti jums priimti pagrįstą sprendimą. Tam į atskirą stulpelį įrašykite kiekvieno projekto pinigų srautus, o tada apskaičiuokite kiekvieno projekto vidinę grąžos normą atskirai:

1 projekto formulė:

=IRR(B2:B7)

Projekto formulė 2:

=IRR(C2:C7)

Projekto formulė 3:

=IRR(D2:D7)

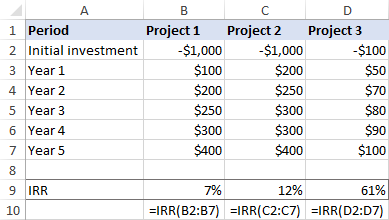
Atsižvelgiant į tai, kad įmonės reikalaujama grąžos norma yra, tarkime, 9 %, 1 projektas turėtų būti atmestas, nes jo vidinė grąžos norma yra tik 7 %.

Kitos dvi investicijos yra priimtinos, nes abi gali duoti didesnę vidinę grąžą nei įmonės ribinė norma. Kurią iš jų pasirinktumėte?

Iš pirmo žvilgsnio 3 projektas atrodo priimtinesnis, nes jo vidinė grąžos norma yra didžiausia. Tačiau jo metiniai pinigų srautai yra daug mažesni nei 2 projekto. Esant situacijai, kai nedidelės investicijos grąžos norma yra labai didelė, įmonės dažnai renkasi investiciją, kurios grąžos procentinė dalis yra mažesnė, bet absoliutinė (dolerio) grąžos vertė didesnė, t. y. 2 projektą.

Išvada tokia: paprastai pirmenybė teikiama didžiausią vidinę grąžos normą turinčioms investicijoms, tačiau, norėdami geriausiai panaudoti savo lėšas, turėtumėte įvertinti ir kitus rodiklius.

4 pavyzdys. Apskaičiuokite sudėtinę metinę augimo normą (CAGR)

Nors "Excel" funkcija IRR skirta vidinei grąžos normai apskaičiuoti, ją taip pat galima naudoti ir sudėtiniam augimo tempui apskaičiuoti. Jums tereikės taip pertvarkyti pradinius duomenis:

• Pirmąją pradinės investicijos vertę laikykite neigiamu skaičiumi, o galutinę vertę - teigiamu skaičiumi.
• Tarpines pinigų srautų vertes pakeiskite nuliais.

Kai tai bus padaryta, parašykite įprastą IRR formulę ir ji pateiks CAGR:

=IRR(B2:B8)

Norėdami įsitikinti, kad rezultatas teisingas, galite jį patikrinti pagal dažniausiai naudojamą CAGR apskaičiavimo formulę:

(galutinė_vertė/pradinė_vertė)^(1/laikotarpių skaičius) -

Kaip parodyta toliau pateiktoje ekrano kopijoje, abi formulės duoda tą patį rezultatą:

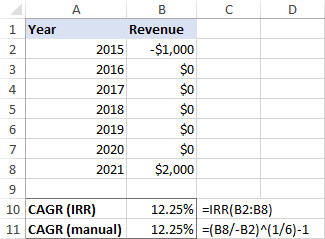
Daugiau informacijos rasite skyriuje Kaip apskaičiuoti CAGR programoje "Excel".

IRR ir NPV "Excel" programoje

Vidinė grąžos norma ir grynoji dabartinė vertė yra dvi glaudžiai susijusios sąvokos, todėl neįmanoma iki galo suprasti IRR nesuprantant NPV. IRR rezultatas yra ne kas kita, o diskonto norma, atitinkanti nulinę grynąją dabartinę vertę.

Esminis skirtumas yra tas, kad NPV yra absoliutus rodiklis, atspindintis vertės, kuri gali būti gauta arba prarasta įgyvendinant projektą, dydį doleriais, o IRR yra procentinė grąžos norma, kurios tikimasi iš investicijos.

Dėl savo skirtingo pobūdžio IRR ir NPV gali "prieštarauti" viena kitai - vieno projekto NPV gali būti didesnė, o kito - didesnė IRR. Kilus tokiam prieštaravimui, finansų ekspertai pataria pirmenybę teikti projektui, kurio grynoji dabartinė vertė yra didesnė.

Kad geriau suprastumėte IRR ir NPV ryšį, panagrinėkite toliau pateiktą pavyzdį. Tarkime, turite projektą, kuriam reikia 1 000 USD pradinių investicijų (B2 langelis) ir 10 % diskonto normos (E1 langelis). Projekto gyvavimo trukmė - penkeri metai, o laukiamos kiekvienų metų pinigų įplaukos nurodytos B3:B7 langeliuose.

Norėdami sužinoti, kiek dabar verti būsimi pinigų srautai, turime apskaičiuoti projekto grynąją dabartinę vertę. Tam naudokite NPV funkciją ir iš jos atimkite pradinę investiciją (kadangi pradinė investicija yra neigiamas skaičius, naudojamas sudėties veiksmas):

=NPV(E1,B3:B7)+B2

Teigiama grynoji dabartinė vertė rodo, kad mūsų projektas bus pelningas:

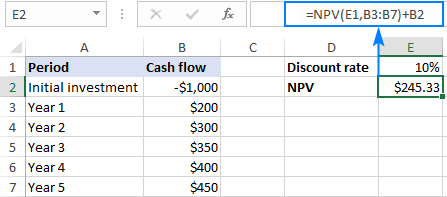
Kokia diskonto norma leis pasiekti, kad grynoji dabartinė vertė būtų lygi nuliui? Atsakymą pateikia ši IRR formulė:

=IRR(B2:B7)

Norėdami tai patikrinti, paimkite pirmiau pateiktą NPV formulę ir diskonto normą (E1) pakeiskite IRR (E4):

=NPV(E4,B3:B7)+B2

Arba IRR funkciją galite įterpti tiesiai į tarifas NPV argumentas:

=NPV(IRR(B2:B7),B3:B7)+B2

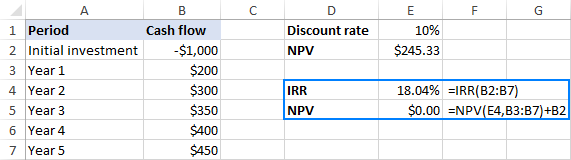
Pirmiau pateiktoje ekrano kopijoje matyti, kad NPV vertė, suapvalinta iki 2 ženklų po kablelio, iš tiesų lygi nuliui. Jei norite sužinoti tikslų skaičių, nustatykite NPV langeliui mokslinį formatą arba pasirinkite rodyti daugiau ženklų po kablelio:

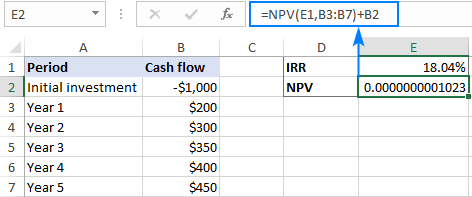
Kaip matote, rezultatas neviršija deklaruojamo 0,00001 proc. tikslumo, todėl galime teigti, kad NPV iš tikrųjų yra lygi 0.

Patarimas. Jei nevisiškai pasitikite "Excel" programos IRR skaičiavimo rezultatu, visada galite jį patikrinti naudodami NPV funkciją, kaip parodyta pirmiau.

Neveikia "Excel" IRR funkcija

Jei "Excel" programoje susidūrėte su tam tikra IRR problema, toliau pateikiami patarimai gali padėti ją išspręsti.

IRR formulė grąžina klaidą #NUM!

Dėl šių priežasčių gali būti grąžinama #NUM! klaida:

• IRR funkcija 20-ojo bandymo metu neranda rezultato iki 0,000001 % tikslumu.
• Pateiktas reikšmės diapazone nėra bent vieno neigiamo ir bent vieno teigiamo pinigų srauto.

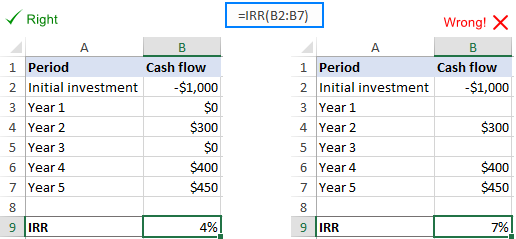
Tuščios reikšmių masyvo ląstelės

Jei vienu ar keliais laikotarpiais neatsiranda pinigų srautų, gali būti, kad liks tuščių langelių reikšmės intervalą. Ir tai yra problemų šaltinis, nes eilutės su tuščiais langeliukais neįtraukiamos į "Excel" vidinės grąžos normos skaičiavimus. Norėdami tai ištaisyti, tiesiog į visus tuščius langelius įrašykite nulines reikšmes. Dabar "Excel" matys teisingus laiko intervalus ir teisingai apskaičiuos vidinę grąžos normą.

Kelios vidinės grąžos normos

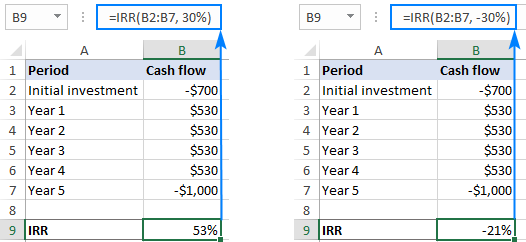
Kai pinigų srautų eilutė keičiasi iš neigiamos į teigiamą arba atvirkščiai daugiau nei vieną kartą, galima rasti daug IRR.

Jei formulės rezultatas toli gražu neatitinka jūsų lūkesčių, patikrinkite spėjamąją vertę - jei IRR lygtį galima išspręsti su keliomis normos vertėmis, grąžinama spėjamajai vertei artimiausia norma.

Galimi sprendimai:

• Darydami prielaidą, kad žinote, kokios grąžos tikitės iš tam tikros investicijos, remkitės savo lūkesčiais kaip spėjimu.
• Kai gaunate daugiau nei vieną IRR tam pačiam pinigų srautui, kaip tikrąją IRR pasirinkite tą, kuri yra arčiausiai įmonės kapitalo kainos.
• Naudokite MIRR funkciją, kad išvengtumėte kelių IRR problemos.

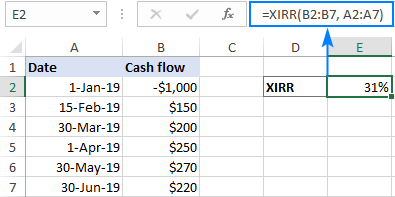
Nereguliarūs pinigų srautų intervalai

"Excel" funkcija IRR skirta dirbti su reguliariais pinigų srautų periodais, pavyzdžiui, savaitės, mėnesio, ketvirčio ar metų laikotarpiais. Jei įplaukos ir išplaukos vyksta nevienodais intervalais, IRR vis tiek laikys, kad intervalai yra vienodi, ir grąžins neteisingą rezultatą. Tokiu atveju vietoj IRR naudokite funkciją XIRR.

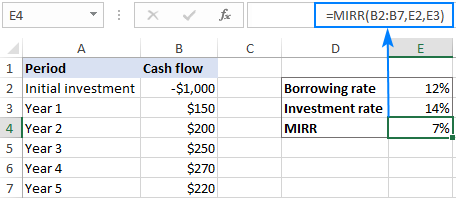
Skirtingos skolinimosi ir reinvestavimo normos

IRR funkcija reiškia, kad projekto pelnas (teigiami pinigų srautai) nuolat reinvestuojamas taikant vidinę grąžos normą. Tačiau realybėje norma, pagal kurią skolinatės pinigus, ir norma, pagal kurią reinvestuojate pelną, dažnai skiriasi. Mūsų laimei, "Microsoft Excel" turi specialią funkciją, kuri pasirūpina šiuo scenarijumi - MIRR funkciją.

Štai kaip atlikti IRR funkciją "Excel" programoje. Norėdami atidžiau susipažinti su šiame vadovėlyje aptartais pavyzdžiais, galite atsisiųsti mūsų pavyzdinį sąsiuvinį IRR funkcijos naudojimas "Excel" programoje. Dėkoju, kad perskaitėte, ir tikiuosi, kad kitą savaitę susitiksime mūsų tinklaraštyje!