Í þessari kennslu muntu læra hvernig á að nota Excel NPV fallið til að reikna út hreint núvirði fjárfestingar og hvernig á að forðast algengar villur þegar þú gerir NPV í Excel.

Núvirði eða Núvirði er kjarnaþáttur fjármálagreiningar sem gefur til kynna hvort verkefni muni skila arði eða ekki. Hvers vegna er hreint núvirði svona mikilvægt? Vegna þess að grundvallarfjárhagshugmyndin heldur því fram að peningar sem hugsanlega er hægt að fá í framtíðinni séu minna virði en sömu upphæð og þú átt núna. Hreint núvirði afföllum sjóðstreymi sem búist er við í framtíðinni aftur til nútímans til að sýna verðmæti þeirra í dag.

Microsoft Excel hefur sérstaka aðgerð til að reikna út NPV, en notkun þess getur verið erfið, sérstaklega fyrir fólk sem hefur litla reynslu í fjármálalíkönum. Tilgangur þessarar greinar er að sýna þér hvernig Excel NPV fallið virkar og benda á hugsanlegar gildrur þegar reiknað er út hreint núvirði röð sjóðstreymis í Excel.

Hvað er nettó. núvirði (NPV)?

Núvirði (NPV) er verðmæti röð sjóðstreymis yfir allan líftíma verkefnis núvirt til dagsins í dag.

Í einföldu máli má skilgreina NPV sem núvirði framtíðarsjóðstreymis að frádregnum upphafsfjárfestingarkostnaði:

NPV = PV framtíðarsjóðstreymis – Upphafsfjárfesting

Til að skilja beturtímabil sem hafa núll sjóðstreymi.

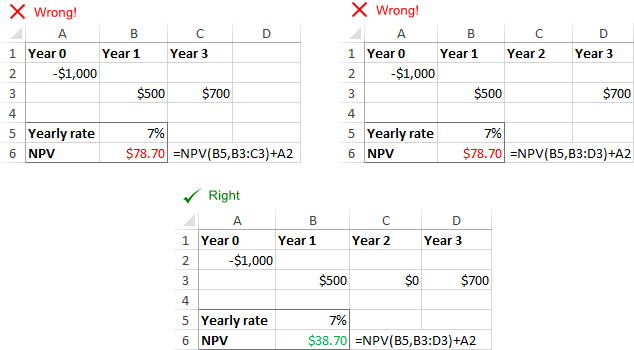
Afsláttarhlutfall samsvarar ekki raunverulegum tímabilum

Excel NPV aðgerðin getur ekki stillt uppgefið gengi að tilteknum tíma tíðni sjálfkrafa, til dæmis árlegt afvöxtunarhlutfall í mánaðarlegt sjóðstreymi. Það er á ábyrgð notanda að gefa upp viðeigandi gengi á tímabili .

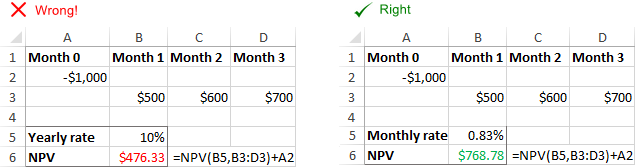
Rangt vaxtasnið

Afsláttur eða vextir verða að vera gefið upp sem hlutfall eða samsvarandi tugatala . Til dæmis er hægt að gefa 10 prósent hlutfallið sem 10% eða 0,1. Ef þú slærð inn hlutfallið sem númer 10 mun Excel meðhöndla það sem 1000% og NPV verður reiknað rangt.

Svona á að nota NPV í Excel til að finna netið. núvirði fjárfestingar. Til að skoða betur formúlurnar sem fjallað er um í þessari kennslu skaltu ekki hika við að hlaða niður sýnishorn af NPV reiknivélinni okkar fyrir Excel.

Þakka þér fyrir að lesa og vonumst til að sjá þig á blogginu okkar í næstu viku!

Fyrir eitt sjóðstreymi er núvirði (PV) reiknað með þessari formúlu:

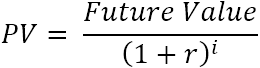
Hvar :

• r – afsláttur eða vextir
• i – sjóðstreymistímabilið

Til dæmis til að fá $110 (framtíðargildi) eftir 1 ár (i), hversu mikið ættir þú að fjárfesta í dag á bankareikningnum þínum sem býður upp á 10% ársvexti (r)? Ofangreind formúla gefur þetta svar:

$110/(1+10%)^1 = $100

Með öðrum orðum, $100 er núvirði $110 sem búist er við að berist í framtíðinni.

Hreint núvirði (NPV) leggur saman núvirði allra framtíðarsjóðstreymis til að koma því á einn stað í nútíðinni. Og vegna þess að hugmyndin um "nettó" er að sýna hversu arðbært verkefnið verður eftir að hafa tekið tillit til stofnfjárfestingar sem þarf til að fjármagna það, er upphæð upphaflegrar fjárfestingar dregin frá summu allra núvirðis:

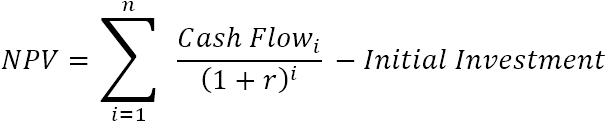
Hvar:

• r – afsláttur eða vextir
• n – fjöldi tímabila
• i – sjóðstreymistímabil

Vegna þess að öll tala sem er ekki núll, hækkuð upp í núllveldið, jafngildir 1, getum við tekið upphaflegu fjárfestinguna með í summan. Vinsamlegast athugaðu að í þessari þéttu útgáfu af NPV formúlunni, i=0, þ.e. upphafsfjárfesting er gerð á tímabilinu 0.

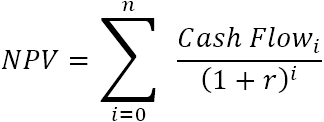
Til dæmis, til að finna NPV fyrir a röð sjóðstreymis (50, 60, 70) núvirtur með 10% og stofnkostnaði$100, þú getur notað þessa formúlu:

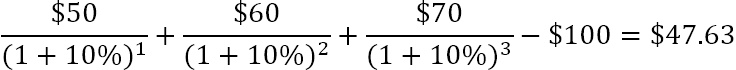
Eða

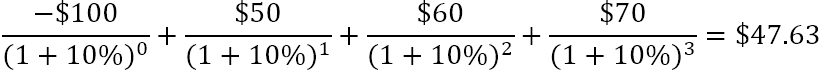
Hvernig hjálpar hreint núvirði við að meta fjárhagsstöðu hagkvæmni fyrirhugaðrar fjárfestingar? Gert er ráð fyrir að fjárfesting með jákvæða NPV sé arðbær og fjárfesting með neikvæðum NPV sé óarðbær. Þetta hugtak er grundvöllur Núvirðisreglunnar , sem segir að þú ættir aðeins að taka þátt í verkefnum með jákvætt nettó núvirði.

Excel NPV fall

The NPV fall í Excel skilar hreinu núvirði fjárfestingar byggt á afslætti eða vöxtum og röð framtíðarsjóðstreymis.

Setjafræði Excel NPV fallsins er sem hér segir:

Hvar:

• Vaxta (áskilið) - afsláttur eða vextir yfir eitt tímabil. Það verður að gefa upp sem prósentu eða samsvarandi aukastaf.
• Value1, [value2], … - tölugildi sem tákna röð af reglulegu sjóðstreymi. Value1 er áskilið, síðari gildi eru valfrjáls. Í nútímaútgáfum af Excel 2007 til 2019 er hægt að koma með allt að 254 gildisrök; í Excel 2003 og eldri – allt að 30 rök.

NPV aðgerðin er fáanleg í Excel 365 - 2000.

Ráð:

• Til að reikna út núvirði lífeyris, notaðu Excel PV fall.
• Til að áætla áætlaða arðsemi fjárfestingar skaltu gera IRR útreikning.

4 hlutir sem þúætti að vita um NPV virkni

Til að tryggja að NPV formúlan þín í Excel reikni rétt, vinsamlegast hafðu í huga þessar staðreyndir:

• Gildi verða að koma fram í lok hvers tímabils . Ef fyrsta sjóðstreymi (upphafleg fjárfesting) á sér stað í byrjun fyrsta tímabils , notaðu eina af þessum NPV formúlum.
• Gildi verður að gefa upp í tímaröð og jafnt í tíma .
• Notaðu neikvæð gildi til að tákna útstreymi (greitt útgreitt) og jákvæð gildi til að tákna innstreymi (móttekið reiðufé ).
• Aðeins tölugildi eru unnin. Tómar hólf, textaframsetning á tölum, rökrétt gildi og villugildi eru hunsuð.

Hvernig Excel NPV aðgerð virkar

Að nota NPV aðgerðina í Excel er svolítið erfiður vegna hvernig aðgerðin er útfærð. Sjálfgefið er að gert sé ráð fyrir að fjárfesting sé gerð einu tímabili fyrir virði1 dagsetningu. Af þessum sökum virkar NPV formúla í sinni hreinu mynd aðeins rétt ef þú gefur upp upphafsfjárfestingarkostnað eitt tímabil héðan í frá , ekki í dag!

Til að sýna þetta skulum við reikna út hreint núvirði handvirkt og með Excel NPV formúlu og berðu saman niðurstöðurnar.

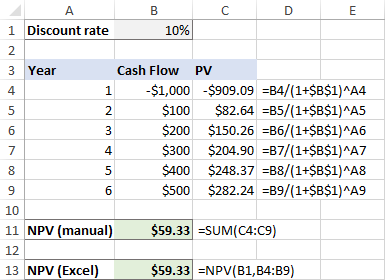
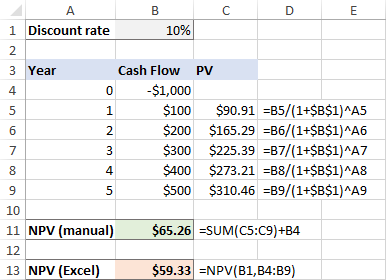
Segjum að þú sért með ávöxtunarkröfu í B1, röð sjóðstreymis í B4:B9 og tímabilsnúmer í A4:A9.

Gefðu upp ofangreindar tilvísanir í þessari almennu PV formúlu:

PV = framtíðvalue/(1+rate)^period

Og þú færð eftirfarandi jöfnu:

=B4/(1+$B$1)^A4

Þessi formúla fer í C4 og er síðan afrituð í reitina fyrir neðan. Vegna snjallrar notkunar á algildum og hlutfallslegum frumutilvísunum, lagar formúlan sig fullkomlega fyrir hverja röð eins og sýnt er á skjámyndinni hér að neðan.

Vinsamlegast athugaðu að við reiknum út núvirði upphafsfjárfestingarinnar líka frá upphaflegu fjárfestingarkostnaði er eftir 1 ár , svo það er líka afsláttur.

Eftir það leggjum við saman öll núgildin:

=SUM(C4:C9)

Og nú skulum við gerðu NPV með Excel fallinu:

=NPV(B1, B4:B9)

Eins og þú sérð passa niðurstöður beggja útreikninga nákvæmlega:

En hvað ef upphafskostnaður á sér stað í byrjun fyrsta tímabils , eins og venjulega?

Þar sem upphaflega fjárfestingin er gerð í dag gildir enginn afsláttur um hana og við bætum einfaldlega þessari upphæð við. að summan af núvirði framtíðarsjóðstreymis (þar sem það er neikvæð tala, er hún í raun dregin frá):

=SUM(C4:C9)+B4

Og í þessu tilviki gefa handvirki útreikningurinn og Excel NPV fallið ávöxtun mismunandi niðurstöður:

Þýðir þetta að við getum ekki treyst á NPV fyrir múla í Excel og þarf að reikna hreint núvirði handvirkt við þessar aðstæður? Auðvitað ekki! Þú þarft bara að fínstilla NPV fallið aðeins eins og útskýrt er í næsta kafla.

Hvernig á að reikna út NPV í Excel

Þegar upphafleg fjárfestinger gert í byrjun fyrsta tímabils , getum við farið með það sem sjóðstreymi í lok fyrra tímabils (þ.e. tímabil 0). Með það í huga eru tvær einfaldar leiðir til að finna NPV í Excel.

Excel NPV formúla 1

Slepptu stofnkostnaði utan gildissviðsins og dragðu hann frá niðurstöðu NPV fallsins . Þar sem upphafskostnaður er venjulega færður inn sem neikvæð tala , framkvæmir þú í raun samlagningaraðgerðina:

Í þessu tilviki skilar Excel NPV fallið bara núvirði ójafns sjóðstreymis. Vegna þess að við viljum "nettó" (þ.e. núvirði framtíðarsjóðstreymis að frádreginni upphaflegri fjárfestingu), drögum við frá upphafskostnað fyrir utan NPV fallið.

Excel NPV formúla 2

Ta með stofnkostnað á bilinu gilda og margfaldaðu niðurstöðuna með (1 + hlutfall).

Í þessu tilviki myndi Excel NPV fallið gefa þér niðurstöðuna frá tímabilinu -1 (eins og upphafleg fjárfesting hafi verið gerð eitt tímabil fyrir tímabilið 0), verðum við að margfalda úttak þess með (1 + r) til að færa NPV eitt tímabil fram í tímann (þ.e. frá i = -1 til i = 0). Vinsamlegast sjáðu samsetta mynd NPV formúlunnar.

Hvaða formúlu á að nota er spurning um persónulegt val þitt. Ég persónulega tel að sá fyrsti sé einfaldari og auðskiljanlegri.

NPV reiknivél í Excel

Nú skulum við sjá hvernig þú getur notað ofangreintformúlur á raunverulegum gögnum til að búa til þinn eigin NPV reiknivél í Excel.

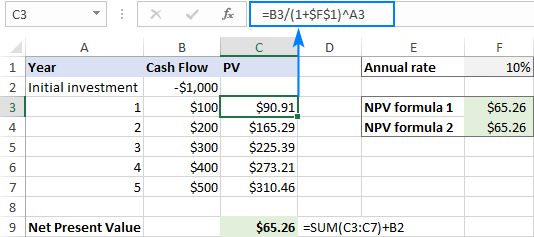
Svo sem þú ert með upphafskostnað í B2, röð framtíðarsjóðstreymis í B3:B7 og ávöxtunarkröfu í F1. Til að finna NPV skaltu nota eina af eftirfarandi formúlum:

NPV formúla 1:

=NPV(F1, B3:B7) + B2

Vinsamlegast athugaðu að fyrsta gildisfrumvarpið er reiðufé flæði á tímabili 1 (B3), stofnkostnaður (B2) er ekki innifalinn.

NPV Formúla 2:

=NPV(F1, B2:B7) * (1+F1)

Þessi formúla inniheldur upphafskostnaður (B2) á bilinu gilda.

Skjámyndin hér að neðan sýnir Excel NPV reiknivélina okkar í aðgerð:

Til að tryggja að Excel NPV okkar formúlur eru réttar, við skulum athuga niðurstöðuna með handvirkum útreikningum.

Í fyrsta lagi finnum við núvirði hvers sjóðstreymis með því að nota PV formúluna sem fjallað er um hér að ofan:

=B3/(1+$F$1)^A3

Næst skaltu leggja saman öll núgildin og draga frá stofnkostnaði við fjárfestingu:

=SUM(C3:C7)+B2

... og sjá að niðurstöður allra þriggja formúlanna eru algjörlega þær sömu.

Athugið. Í þessu dæmi erum við að fást við árlegt sjóðstreymi og ársvexti. Ef þú ætlar að finna fjórðungslega eða mánaðarlega NPV í Excel, vertu viss um að stilla afsláttarhlutfallið í samræmi við það eins og útskýrt er í þessu dæmi.

Mismunur á PV og NPV í Excel

Í fjármálum eru bæði PV og NPV notuð til að mæla núverandi virði framtíðarsjóðstreymis með því að núvirða framtíðarupphæðir. Enþau eru mismunandi á einn mikilvægan hátt:

• Núvirði (PV) - vísar til alls framtíðarinnstreymi sjóðs á tilteknu tímabili.
• Nettó nútíð gildi (NPV) – er mismunurinn á núvirði innstreymis peninga og núvirðis útstreymis peninga.

Með öðrum orðum, PV tekur aðeins til innstreymis peninga, á meðan NPV tekur einnig tillit til fyrir upphaflega fjárfestingu eða útgjöld, sem gerir það að nettótölu.

Í Microsoft Excel eru tveir grundvallarmunir á aðgerðunum:

• NPV-fallið getur reiknað ójafnt (breytilegt) sjóðstreymi. PV fallið krefst þess að sjóðstreymi sé stöðugt yfir allan líftíma fjárfestingar.
• Með NPV þarf sjóðstreymi að eiga sér stað í lok hvers tímabils. PV getur séð um sjóðstreymi sem á sér stað í lok og í upphafi tímabils.

Mismunur á NPV og XNPV í Excel

XNPV er enn ein fjármálaaðgerðin í Excel sem reiknar út hreint núvirði fjárfestingar. Aðalmunurinn á aðgerðunum er sem hér segir:

• NPV telur öll tímabil vera jöfn .
• XNPV gerir þér kleift að tilgreina dagsetningar sem samsvara hverju peningaflæði. Af þessum sökum er XNPV aðgerðin mun nákvæmari þegar tekist er á við röð sjóðstreymis með óreglulegu millibili .

Ólíkt NPV er Excel XNPV aðgerðin útfærð "venjulega " - fyrsta gildið samsvarar útstreyminu sem á sér stað klupphaf fjárfestingarinnar. Allt sjóðstreymi í röð er núvirt miðað við 365 daga ár.

Hvað varðar setningafræði, hefur XNPV fallið eitt viðbótarrök:

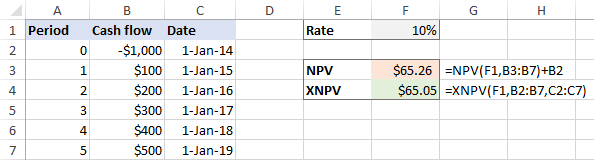
Sem dæmi , við skulum nota báðar aðgerðirnar á sama gagnasettinu, þar sem F1 er afvöxtunarhlutfallið, B2:B7 er sjóðstreymi og C2:C7 eru dagsetningar:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Ef sjóðstreyminu er dreift jafnt í gegnum fjárfestinguna skila NPV og XNPV föllin mjög nánum tölum:

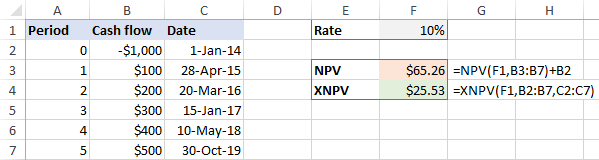
Í ef um er að ræða óreglulegt millibil er munur á niðurstöðum mjög marktækur:

Algengar villur við útreikning á NPV í Excel

Vegna þess að alveg sértæk útfærsla á NPV fallinu, margar villur eru gerðar við útreikning á hreinu núvirði í Excel. Einföld dæmin hér að neðan sýna dæmigerðustu villurnar og hvernig á að forðast þær.

Óreglulegt millibil

Excel NPV fallið gerir ráð fyrir að öll sjóðstreymistímabil séu jöfn . Ef þú gefur upp mismunandi millibili, td ár og ársfjórðunga eða mánuði, verður hreint núvirði rangt vegna ósamstæðra tímabila.

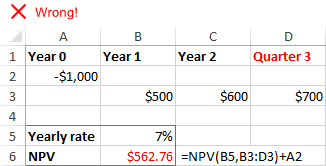
Tímabil eða sjóðstreymi vantar

NPV í Excel þekkir ekki sleppt punktum og hunsar tómar reiti. Til að reikna NPV rétt, vinsamlegast vertu viss um að gefa upp samfellda mánuði, ársfjórðunga eða ár og gefa upp núll gildi fyrir tíma