В този урок ще научите как да използвате функцията NPV на Excel за изчисляване на нетната настояща стойност на инвестиция и как да избягвате често срещани грешки при изчисляване на NPV в Excel.

Нетна настояща стойност или нетна настояща стойност е основен елемент на финансовия анализ, който показва дали даден проект ще бъде печеливш или не. Защо нетната настояща стойност е толкова важна? Защото основната финансова концепция гласи, че парите, които потенциално могат да бъдат получени в бъдеще, струват по-малко от същата сума пари, с която разполагате в момента. Нетната настояща стойност дисконтира паричните потоци, очаквани в бъдеще, обратно към настоящетода покажат днешната си стойност.

Microsoft Excel разполага със специална функция за изчисляване на NPV, но използването ѝ може да бъде трудно, особено за хора, които имат малък опит във финансовото моделиране. Целта на тази статия е да ви покаже как работи функцията NPV на Excel и да посочи възможните капани при изчисляване на нетната настояща стойност на поредица от парични потоци в Excel.

Какво представлява нетната настояща стойност (ННС)?

Нетна настояща стойност (NPV) е стойността на поредица от парични потоци през целия живот на проекта, дисконтирани към настоящето.

На прост език NPV може да се определи като настоящата стойност на бъдещите парични потоци, намалена с първоначалните инвестиционни разходи:

NPV = PV на бъдещите парични потоци - Първоначална инвестиция

За да разберем по-добре идеята, нека се задълбочим малко в математиката.

За един паричен поток настоящата стойност (PV) се изчислява по тази формула:

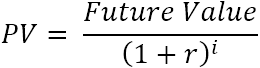
Къде:

• r - сконтов или лихвен процент
• i - периодът на паричния поток

Например, за да получите 110 USD (бъдеща стойност) след 1 година (i), колко трябва да инвестирате днес в банковата си сметка, която предлага 10% годишен лихвен процент (r)? Горната формула дава този отговор:

$110/(1+10%)^1 = $100

С други думи, 100 USD е настоящата стойност на 110 USD, които се очаква да бъдат получени в бъдеще.

Нетната настояща стойност (ННС) сумира настоящите стойности на всички бъдещи парични потоци, за да ги сведе до една точка в настоящето. И тъй като идеята на "нетната" стойност е да покаже колко печеливш ще бъде проектът, след като се отчете първоначалната капиталова инвестиция, необходима за финансирането му, сумата на първоначалната инвестиция се изважда от сумата на всички настоящи стойности:

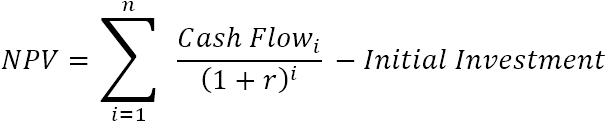
Къде:

• r - сконтов или лихвен процент
• n - броят на времевите периоди
• i - периодът на паричния поток

Тъй като всяко ненулево число, повдигнато до нулата, е равно на 1, можем да включим първоначалната инвестиция в сумата. Моля, обърнете внимание, че в тази компактна версия на формулата за NPV i=0, т.е. първоначалната инвестиция се прави в период 0.

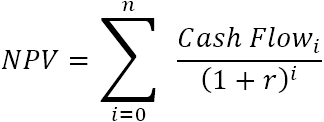
Например, за да намерите NPV за поредица от парични потоци (50, 60, 70), дисконтирани с 10% и първоначални разходи от 100 USD, можете да използвате тази формула:

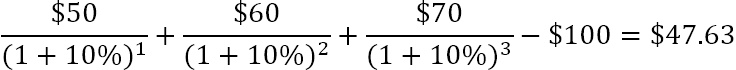
Или

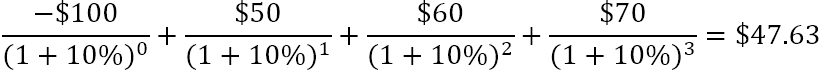
Как нетната настояща стойност помага при оценката на финансовата жизнеспособност на предложена инвестиция? Приема се, че инвестиция с положителна нетна настояща стойност ще бъде печеливша, а инвестиция с отрицателна нетна настояща стойност ще бъде непечеливша. Тази концепция е в основата на Правило за нетната настояща стойност , която гласи, че трябва да участвате само в проекти с положителна нетна настояща стойност.

Функция NPV на Excel

Функцията NPV в Excel връща нетната настояща стойност на дадена инвестиция въз основа на дисконтов или лихвен процент и поредица от бъдещи парични потоци.

Синтаксисът на функцията NPV на Excel е следният:

Къде:

• Оценка (задължително) - сконтовият или лихвеният процент за един период. Трябва да се посочи като процент или съответно десетично число.
• Стойност1, [стойност2], ... - числови стойности, представляващи поредица от редовни парични потоци. Стойност1 В съвременните версии на Excel от 2007 до 2019 г. могат да бъдат предоставени до 254 аргумента за стойности, а в Excel 2003 и по-старите - до 30 аргумента.

Функцията NPV е налична в Excel 365 - 2000.

Съвети:

• За да изчислите настоящата стойност на анюитета, използвайте функцията PV на Excel.
• За да оцените прогнозираната възвръщаемост на инвестицията, направете изчисление на вътрешната норма на възвръщаемост.

4 неща, които трябва да знаете за функцията NPV

За да сте сигурни, че формулата ви за NPV в Excel се изчислява правилно, имайте предвид тези факти:

• Стойностите трябва да се появяват в в края на всеки период Ако първият паричен поток (първоначалната инвестиция) възникне на начало на първия период , използвайте една от тези формули за NPV.
• Стойностите трябва да се предоставят в хронологичен ред и на равни интервали във времето .
• Използвайте отрицателен стойности за представяне на изходящите потоци (изплатени парични средства) и положителен стойности, които представляват входящи потоци (получени парични средства).
• Само цифрови стойности Празните клетки, текстовото представяне на числа, логическите стойности и стойностите за грешки се игнорират.

Как работи функцията NPV на Excel

Използването на функцията NPV в Excel е малко трудно поради начина, по който е реализирана функцията. По подразбиране се приема, че инвестицията е направена един период преди стойност1 Поради тази причина формулата за NPV в чист вид работи правилно само ако предоставите първоначалните инвестиционни разходи един период от сега , не и днес!

За да илюстрираме това, нека да изчислим нетната настояща стойност ръчно и с формулата NPV на Excel и да сравним резултатите.

Да речем, че имате дисконтов процент в Б1, поредица от парични потоци в Б4:Б9 и номера на периода в А4:А9.

Поставете горните препратки в тази обща формула за PV:

PV = бъдеща стойност/(1+ ставка)^период

И ще получите следното уравнение:

=B4/(1+$B$1)^A4

Тази формула отива в C4 и след това се копира в клетките по-долу. Благодарение на умелото използване на абсолютни и относителни препратки към клетките, формулата се настройва перфектно за всеки ред, както е показано на снимката по-долу.

Моля, обърнете внимание, че изчисляваме и настоящата стойност на първоначалната инвестиция, тъй като разходите за първоначалната инвестиция са след 1 година , така че той също е намален.

След това се сумират всички настоящи стойности:

=SUM(C4:C9)

А сега нека направим NPV с функцията на Excel:

=NPV(B1, B4:B9)

Както можете да видите, резултатите от двете изчисления съвпадат точно:

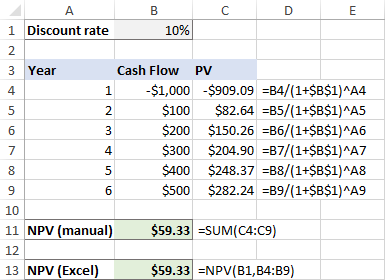
Но какво ще стане, ако първоначалните разходи се извършват в начало на първия период , както обикновено се случва?

Тъй като първоначалната инвестиция е направена днес, за нея не се прилага дисконтиране и ние просто прибавяме тази сума към сумата на настоящите стойности на бъдещите парични потоци (тъй като това е отрицателно число, то всъщност се изважда):

=SUM(C4:C9)+B4

И в този случай ръчното изчисление и функцията NPV на Excel дават различни резултати:

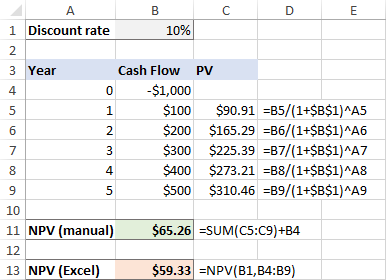
Означава ли това, че не можем да разчитаме на формулата NPV в Excel и трябва да изчислим ръчно нетната настояща стойност в тази ситуация? Разбира се, не! Просто ще трябва да коригирате малко функцията NPV, както е обяснено в следващия раздел.

Как да изчислим NPV в Excel

Когато първоначалната инвестиция е направена в начало на първия период , можем да го разглеждаме като паричен поток в края на предходния период (т.е. период 0). Имайки предвид това, има два прости начина за намиране на NPV в Excel.

Формула за NPV на Excel 1

Оставете първоначалните разходи извън диапазона от стойности и ги извадете от резултата на функцията NPV. Тъй като първоначалните разходи обикновено се въвеждат като отрицателно число , всъщност извършвате операцията събиране:

В този случай функцията NPV на Excel просто връща настоящата стойност на неравномерните парични потоци. Тъй като искаме "нетна" стойност (т.е. настоящата стойност на бъдещите парични потоци минус първоначалната инвестиция), изваждаме първоначалните разходи извън функцията NPV.

Формула за NPV на Excel 2

Включете първоначалните разходи в диапазона от стойности и умножете резултата по (1 + ставка).

В този случай функцията NPV на Excel би ви дала резултат за период -1 (все едно първоначалната инвестиция е направена един период преди период 0), трябва да умножим резултата ѝ по (1 + r), за да пренесем NPV напред във времето с един период (т.е. от i = -1 до i = 0). Моля, вижте компактната форма на формулата за NPV.

Коя формула да използвате, е въпрос на лично предпочитание. Аз лично смятам, че първата е по-проста и по-лесна за разбиране.

Калкулатор на NPV в Excel

Сега нека видим как можете да използвате горните формули върху реални данни, за да си направите собствен калкулатор на NPV в Excel.

Да предположим, че разполагате с първоначалните разходи в B2, поредица от бъдещи парични потоци в B3:B7 и изискваната норма на възвръщаемост в F1. За да намерите NPV, използвайте една от следните формули:

Формула за NPV 1:

=NPV(F1, B3:B7) + B2

Моля, обърнете внимание, че първият аргумент за стойността е паричният поток през период 1 (B3), като първоначалните разходи (B2) не са включени.

Формула за НПВ 2:

=NPV(F1, B2:B7) * (1+F1)

Тази формула включва първоначалните разходи (B2) в диапазона от стойности.

Снимката на екрана по-долу показва нашия калкулатор на NPV в Excel в действие:

За да се уверим, че формулите за NPV на Excel са правилни, нека проверим резултата с ръчни изчисления.

Първо, намираме настоящата стойност на всеки паричен поток, като използваме формулата PV, разгледана по-горе:

=B3/(1+$F$1)^A3

След това съберете всички настоящи стойности и извадете първоначалната цена на инвестицията:

=SUM(C3:C7)+B2

... и ще видите, че резултатите от трите формули са абсолютно еднакви.

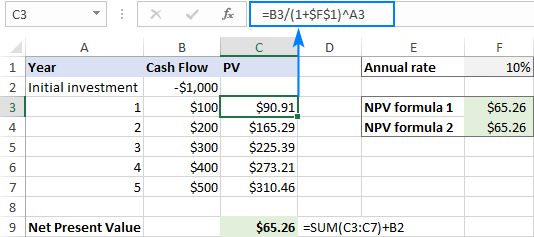
Забележка. В този пример става въпрос за годишни парични потоци и годишен лихвен процент. Ако трябва да намерите тримесечно или месечно NPV в Excel, не забравяйте да коригирате съответно нормата на дисконтиране, както е обяснено в този пример.

Разлика между PV и NPV в Excel

Във финансите както PV, така и NPV се използват за измерване на текущата стойност на бъдещите парични потоци чрез дисконтиране на бъдещите суми към настоящето. Но те се различават по един важен начин:

• Настояща стойност (PV) - отнася се за всички бъдещи парични постъпления през даден период.
• Нетна настояща стойност (NPV) - представлява разликата между настоящата стойност на входящите парични потоци и настоящата стойност на изходящите парични потоци.

С други думи, PV отчита само входящите парични потоци, докато NPV отчита и първоначалната инвестиция или разход, което я прави нетна величина.

В Microsoft Excel има две съществени разлики между функциите:

• Функцията NPV може да изчислява неравномерни (променливи) парични потоци. Функцията PV изисква паричните потоци да са постоянни през целия живот на инвестицията.
• При NPV паричните потоци трябва да възникват в края на всеки период. PV може да обработва парични потоци, които възникват в края и в началото на периода.

Разлика между NPV и XNPV в Excel

XNPV е още една финансова функция на Excel, която изчислява нетната настояща стойност на дадена инвестиция. Основната разлика между функциите е следната:

• NPV счита, че всички времеви периоди са равен .
• XNPV ви позволява да посочите дати, които съответстват на всеки паричен поток. Поради тази причина функцията XNPV е много по-прецизна, когато работи с поредица от парични потоци на неравномерни интервали .

За разлика от NPV, функцията XNPV на Excel е реализирана "нормално" - първата стойност съответства на изходящия поток, който възниква в началото на инвестицията. Всички следващи парични потоци се дисконтират на базата на 365-дневна година.

По отношение на синтаксиса функцията XNPV има един допълнителен аргумент:

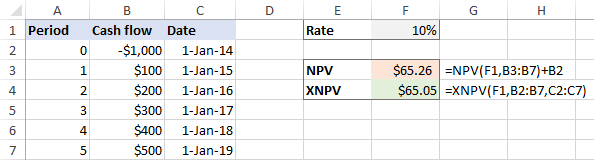
Като пример нека използваме и двете функции за един и същ набор от данни, където F1 е дисконтовият процент, B2:B7 са парични потоци, а C2:C7 са дати:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Ако паричните потоци са разпределени равномерно през инвестицията, функциите NPV и XNPV дават много близки стойности:

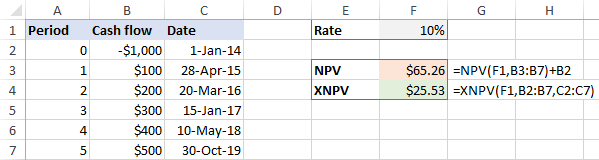
В случай на неравномерни интервали , разликата между резултатите е много съществена:

Често срещани грешки при изчисляване на NPV в Excel

Поради доста специфичната реализация на функцията NPV се допускат много грешки при изчисляване на нетната настояща стойност в Excel. Простите примери по-долу показват най-типичните грешки и как да ги избегнем.

Нередовни интервали

Функцията NPV на Excel приема, че всички периоди на парични потоци са равен Ако предоставите различни интервали, например години и тримесечия или месеци, нетната настояща стойност ще бъде невярна поради несъгласуваните периоди.

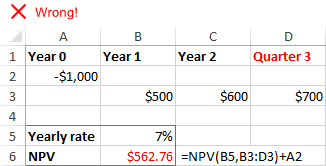
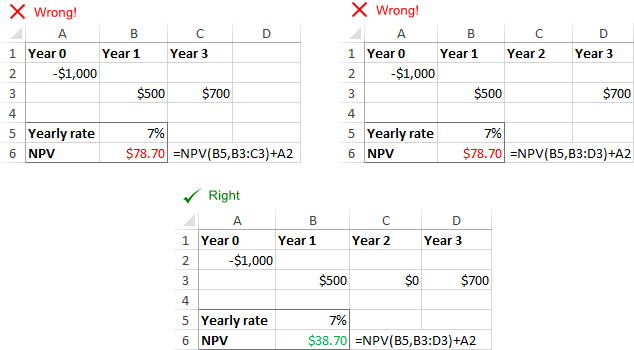
Липсващи периоди или парични потоци

NPV в Excel не разпознава пропуснати периоди и пренебрегва празни клетки. За да изчислите правилно NPV, моля, не забравяйте да предоставите последователни месеци, тримесечия или години и доставка нула стойности за периоди от време, които имат нулеви парични потоци.

Нормата на дисконтиране не съответства на действителните периоди от време

Функцията NPV на Excel не може автоматично да адаптира предоставената ставка към зададените времеви честоти, например годишна ставка за дисконтиране на месечни парични потоци. Отговорност на потребителя е да предостави подходяща ставка за период .

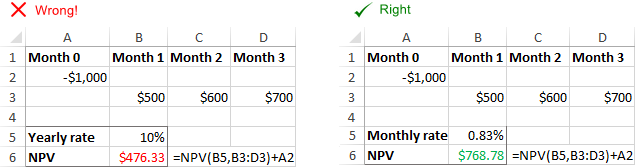
Неправилен формат на скоростта

Сконтовият или лихвеният процент трябва да бъде представен като процент или съответните десетично число . Например 10-процентната ставка може да бъде предоставена като 10% или 0,1. Ако въведете ставката като число 10, Excel ще я третира като 1000% и NPV ще бъде изчислена погрешно.

Ето как да използвате NPV в Excel, за да намерите нетната настояща стойност на дадена инвестиция. За да разгледате по-отблизо формулите, разгледани в този урок, моля, не се колебайте да изтеглите нашия примерен калкулатор за NPV за Excel.

Благодарим ви за четенето и се надяваме да се видим в нашия блог следващата седмица!