I denne vejledning lærer du, hvordan du bruger Excel NPV-funktionen til at beregne nettonutidsværdien af en investering, og hvordan du undgår almindelige fejl, når du laver NPV i Excel.

Nettonutidsværdi eller nuværende nettoværdi er et centralt element i den finansielle analyse, der viser, om et projekt vil være rentabelt eller ej. Hvorfor er nettonutidsværdien så vigtig? Fordi det grundlæggende finansielle koncept siger, at penge, der potentielt kan modtages i fremtiden, er mindre værd end det samme beløb, som du har lige nu. Nettonutidsværdien diskonterer de forventede pengestrømme i fremtiden tilbage til nutiden.for at vise, hvad de er værd i dag.

Microsoft Excel har en særlig funktion til beregning af NPV, men brugen af den kan være vanskelig, især for folk, der har lidt erfaring med finansiel modellering. Formålet med denne artikel er at vise dig, hvordan Excel NPV-funktionen fungerer, og påpege mulige faldgruber, når du beregner nettonutidsværdien af en række pengestrømme i Excel.

Hvad er nettonutidsværdi (NPV)?

Nettonutidsværdi (NPV) er værdien af en række pengestrømme i hele projektets levetid diskonteret til nutid.

I enkle vendinger kan NPV defineres som nutidsværdien af fremtidige pengestrømme minus de oprindelige investeringsomkostninger:

NPV = PV af fremtidige pengestrømme - Oprindelig investering

For at forstå idéen bedre, skal vi grave lidt dybere ned i matematikken.

For en enkelt pengestrøm beregnes nutidsværdien (PV) med denne formel:

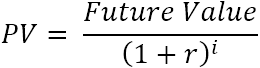
Hvor:

• r - diskontoen eller rentesatsen
• i - pengestrømsperioden

For eksempel, for at få 110 $ (fremtidig værdi) efter 1 år (i), hvor meget skal du så investere i dag på din bankkonto, som giver 10 % årlig rente (r)? Ovenstående formel giver dette svar:

$110/(1+10%)^1 = $100

Med andre ord er 100 USD nutidsværdien af 110 USD, som forventes at blive modtaget i fremtiden.

Nettonutidsværdien (NPV) lægger nutidsværdierne af alle fremtidige pengestrømme sammen for at bringe dem til et enkelt punkt i nutiden. Og da idéen med "netto" er at vise, hvor rentabelt projektet vil være efter at have taget højde for den indledende kapitalinvestering, der er nødvendig for at finansiere det, trækkes beløbet for den indledende investering fra summen af alle nutidsværdier:

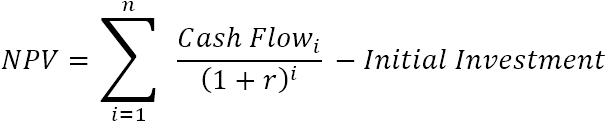
Hvor:

• r - diskontoen eller rentesatsen
• n - antallet af tidsperioder
• i - pengestrømsperioden

Da ethvert tal, der ikke er nul, og som er hævet til nul potens, er lig med 1, kan vi medregne den oprindelige investering i summen. Bemærk venligst, at i denne kompakte version af NPV-formlen er i=0, dvs. den oprindelige investering foretages i periode 0.

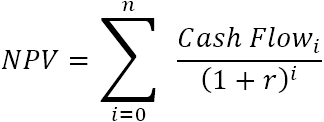
For eksempel kan du bruge denne formel til at finde NPV for en række pengestrømme (50, 60, 70) diskonteret med 10 % og en startpris på 100 $ for at finde NPV for en række pengestrømme (50, 60, 70):

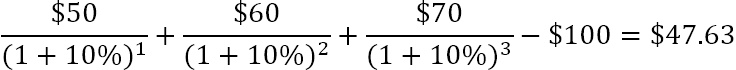
Eller

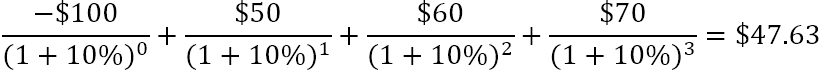
Hvordan hjælper nettonutidsværdien med at vurdere den finansielle levedygtighed af en foreslået investering? Det antages, at en investering med en positiv NPV vil være rentabel, og at en investering med en negativ NPV vil være urentabel. Dette begreb er grundlaget for den Reglen om nettonutidsværdi , som siger, at man kun bør engagere sig i projekter med en positiv nettonutidsværdi.

Excel NPV-funktion

NPV-funktionen i Excel returnerer nettonutidsværdien af en investering baseret på en diskonteringsrente eller rentesats og en række fremtidige pengestrømme.

Syntaksen for Excel NPV-funktionen er som følger:

Hvor:

• Vurder (påkrævet) - diskontoen eller rentesatsen for en periode. Den skal angives som en procentdel eller et tilsvarende decimaltal.
• Værdi1, [værdi2], ... - numeriske værdier, der repræsenterer en række regelmæssige pengestrømme. Værdi1 er påkrævet, efterfølgende værdier er valgfrie. I de moderne versioner af Excel 2007 til 2019 kan der angives op til 254 værdiargumenter; i Excel 2003 og ældre - op til 30 argumenter.

NPV-funktionen er tilgængelig i Excel 365 - 2000.

Tips:

• For at beregne nutidsværdien af en annuitetsrente skal du bruge Excel PV-funktionen.
• For at estimere et forventet investeringsafkast skal du foretage en IRR-beregning.

4 ting, du bør vide om NPV-funktionen

For at sikre, at din NPV-formel i Excel beregner korrekt, skal du huske på følgende fakta:

• Værdierne skal forekomme på den ved udgangen af hver periode Hvis den første pengestrøm (initialinvestering) sker på den begyndelsen af den første periode , bruge en af disse NPV-formler.
• Værdierne skal angives i kronologisk rækkefølge og med lige store tidsafstande .
• Brug negativ værdier til at repræsentere udbetalinger (udbetalte kontanter) og positiv værdier til at repræsentere indbetalinger (modtagne penge).
• Kun numeriske værdier Tomme celler, tekstrepræsentationer af tal, logiske værdier og fejlværdier ignoreres.

Sådan fungerer Excel NPV-funktionen

Det er lidt vanskeligt at bruge NPV-funktionen i Excel på grund af den måde, som funktionen er implementeret på. Som standard antages det, at en investering foretages en periode før den værdi1 Derfor fungerer en NPV-formel i sin rene form kun korrekt, hvis man angiver de oprindelige investeringsomkostninger en periode fra nu , ikke i dag!

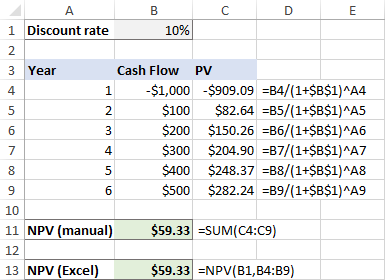
Lad os illustrere dette ved at beregne nettonutidsværdien manuelt og med en Excel NPV-formel og sammenligne resultaterne.

Lad os sige, at du har en diskonteringssats i B1, en række pengestrømme i B4:B9 og periodetal i A4:A9.

Angiv ovenstående referencer i denne generiske PV-formel:

PV = fremtidig værdi/(1+kurs)^periode

Og du får følgende ligning:

=B4/(1+$B$1)^A4

Denne formel går til C4 og kopieres derefter til nedenstående celler. På grund af den smarte brug af absolutte og relative cellehenvisninger tilpasses formlen perfekt til hver række, som vist i skærmbilledet nedenfor.

Bemærk venligst, at vi også beregner nutidsværdien af den oprindelige investering, da den oprindelige investeringsomkostning er efter 1 år , så den er også nedsat.

Derefter summerer vi alle de nuværende værdier:

=SUM(C4:C9)

Og nu skal vi lave NPV med Excel-funktionen:

=NPV(B1, B4:B9)

Som du kan se, stemmer resultaterne af begge beregninger nøjagtigt overens:

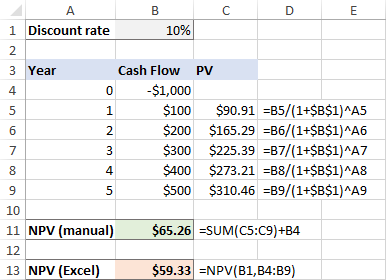
Men hvad nu, hvis den første udgift sker på den starten af den første periode , som den typisk gør?

Fordi den oprindelige investering foretages i dag, anvendes der ingen diskontering, og vi lægger simpelthen dette beløb til summen af nutidsværdierne af fremtidige pengestrømme (da det er et negativt tal, trækkes det faktisk fra):

=SUM(C4:C9)+B4

Og i dette tilfælde giver den manuelle beregning og Excel NPV-funktionen forskellige resultater:

Betyder det, at vi ikke kan stole på NPV-formlen i Excel og skal beregne nettonutidsværdien manuelt i denne situation? Selvfølgelig ikke! Du skal bare justere NPV-funktionen lidt, som forklaret i næste afsnit.

Sådan beregner du NPV i Excel

Når den oprindelige investering foretages på den starten af den første periode kan vi behandle den som en pengestrøm ved udgangen af den foregående periode (dvs. periode 0). Med dette i tankerne er der to enkle måder at finde NPV på i Excel.

Excel NPV-formel 1

Lad den oprindelige udgift ligge uden for værdiintervallet og træk den fra NPV-funktionens resultat. Da den oprindelige udgift typisk angives som en negativt tal , udfører du faktisk additionsoperationen:

I dette tilfælde returnerer Excel NPV-funktionen blot nutidsværdien af ujævne pengestrømme. Da vi ønsker "netto" (dvs. nutidsværdien af fremtidige pengestrømme minus den oprindelige investering), fratrækker vi de oprindelige omkostninger uden for NPV-funktionen.

Excel NPV-formel 2

Medtag de oprindelige omkostninger i værdiintervallet og multiplicer resultatet med (1 + sats).

I dette tilfælde ville Excel NPV-funktionen give dig resultatet fra periode -1 (som om den oprindelige investering blev foretaget en periode før periode 0), vi skal gange dens output med (1 + r) for at bringe NPV fremad en periode i tiden (dvs. fra i = -1 til i = 0). Se den kompakte form af NPV-formlen.

Hvilken formel du skal bruge, er et spørgsmål om din personlige præference. Personligt mener jeg, at den første er enklere og lettere at forstå.

NPV-beregner i Excel

Lad os nu se, hvordan du kan bruge ovenstående formler på rigtige data til at lave din egen NPV-beregner i Excel.

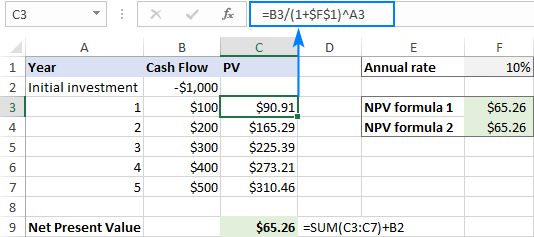
Antag, at du har den oprindelige udgift i B2, en række fremtidige pengestrømme i B3:B7 og den krævede afkastningsgrad i F1. For at finde NPV skal du bruge en af følgende formler:

NPV-formel 1:

=NPV(F1, B3:B7) + B2

Bemærk venligst, at det første værdiargument er pengestrømmen i periode 1 (B3), de oprindelige omkostninger (B2) er ikke medtaget.

NPV-formel 2:

=NPV(F1, B2:B7) * (1+F1)

Denne formel omfatter de oprindelige omkostninger (B2) i værdiintervallet.

Nedenstående skærmbillede viser vores Excel NPV-beregner i aktion:

For at sikre os, at vores Excel NPV-formler er korrekte, skal vi kontrollere resultatet med manuelle beregninger.

Først finder vi nutidsværdien af hver enkelt pengestrøm ved hjælp af den ovenfor beskrevne formel for PV:

=B3/(1+$F$1)^A3

Herefter skal du lægge alle nutidsværdierne sammen og trække de oprindelige investeringsomkostninger fra:

=SUM(C3:C7)+B2

... og se, at resultaterne af alle tre formler er fuldstændig ens.

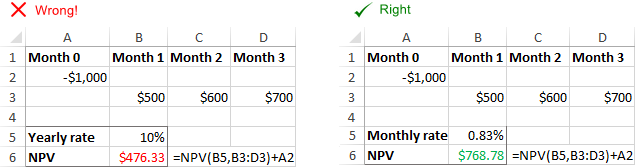
Bemærk. I dette eksempel er der tale om årlige pengestrømme og årlig rente. Hvis du skal finde kvartalsvis eller månedlig NPV i Excel, skal du sørge for at justere diskonteringssatsen i overensstemmelse hermed, som forklaret i dette eksempel.

Forskellen mellem PV og NPV i Excel

Inden for finanssektoren bruges både PV og NPV til at måle den aktuelle værdi af fremtidige pengestrømme ved at diskontere fremtidige beløb til nutiden, men de adskiller sig fra hinanden på en vigtig måde:

• Nutidsværdi (PV) - refererer til alle fremtidige pengestrømme i en given periode.
• Nettonutidsværdi (NPV) - er forskellen mellem nutidsværdien af indgående pengestrømme og nutidsværdien af udgående pengestrømme.

Med andre ord tager PV kun højde for pengestrømmene, mens NPV også tager højde for den oprindelige investering eller udgift, hvilket gør det til et nettotal.

I Microsoft Excel er der to væsentlige forskelle mellem funktionerne:

• NPV-funktionen kan beregne ujævne (variable) pengestrømme. PV-funktionen kræver, at pengestrømmene er konstante i hele investeringens levetid.
• Med NPV skal pengestrømmene ske i slutningen af hver periode. PV kan håndtere pengestrømme, der sker både i slutningen og i begyndelsen af en periode.

Forskellen mellem NPV og XNPV i Excel

XNPV er endnu en Excel-finansfunktion, der beregner nettonutidsværdien af en investering. Den primære forskel mellem funktionerne er følgende:

• NPV anser alle tidsperioder for at være lige .
• XNPV giver dig mulighed for at angive datoer, der svarer til hver enkelt pengestrøm. Derfor er XNPV-funktionen meget mere præcis, når der er tale om en serie af pengestrømme på uregelmæssige intervaller .

I modsætning til NPV er Excel XNPV-funktionen implementeret "normalt" - den første værdi svarer til den udstrømning, der sker i begyndelsen af investeringen. Alle efterfølgende pengestrømme diskonteres på grundlag af et år med 365 dage.

Med hensyn til syntaks har XNPV-funktionen et ekstra argument:

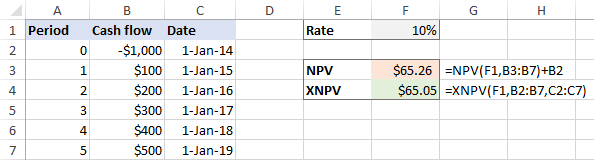
Lad os som eksempel bruge begge funktioner på det samme datasæt, hvor F1 er diskonteringssatsen, B2:B7 er pengestrømme og C2:C7 er datoer:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Hvis pengestrømmene er distribueret jævnt gennem investeringen, giver NPV- og XNPV-funktionerne meget tætte tal:

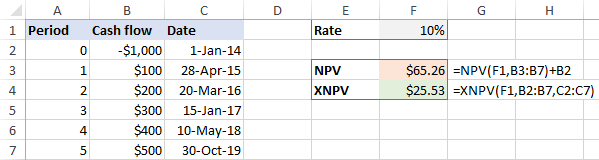
I tilfælde af uregelmæssige intervaller , er forskellen mellem resultaterne meget betydelig:

Almindelige fejl ved beregning af NPV i Excel

På grund af en ret specifik implementering af NPV-funktionen begås der mange fejl, når man beregner nettonutidsværdi i Excel. De enkle eksempler nedenfor viser de mest typiske fejl, og hvordan man undgår dem.

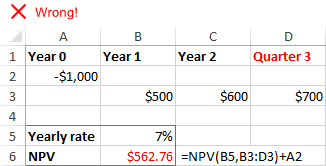
Uregelmæssige intervaller

Excel NPV-funktionen forudsætter, at alle pengestrømsperioder er lige Hvis du angiver forskellige intervaller, f.eks. år og kvartaler eller måneder, vil nettonutidsværdien være forkert på grund af usammenhængende tidsperioder.

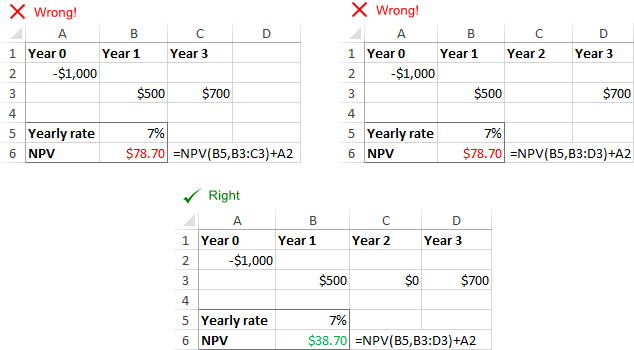
Manglende perioder eller pengestrømme

NPV i Excel genkender ikke udeladte perioder og ignorerer tomme celler. For at beregne NPV korrekt skal du sørge for at angive i træk måneder, kvartaler eller år og forsyning nul værdier for tidsperioder, der har nul pengestrømme.

Diskonteringssatsen svarer ikke til de faktiske tidsperioder

Excel NPV-funktionen kan ikke automatisk justere den leverede sats til de givne tidsfrekvenser, f.eks. årlig diskonteringssats til månedlige pengestrømme. Det er brugerens ansvar at angive en passende sats pr. periode .

Forkert satsformat

Diskontoen eller rentesatsen skal angives som en procentdel eller tilsvarende decimaltal F.eks. kan satsen på 10 % angives som 10 % eller 0,1. Hvis du indtaster satsen som tal 10, vil Excel behandle den som 1000 %, og NPV vil blive beregnet forkert.

Sådan bruger du NPV i Excel til at finde nettonutidsværdien af en investering. Hvis du vil se nærmere på formlerne i denne vejledning, er du velkommen til at downloade vores NPV-beregner til Excel for at se nærmere på dem.

Tak fordi du læste med, og vi håber at se dig på vores blog i næste uge!