Trong hướng dẫn này, bạn sẽ học cách sử dụng hàm NPV trong Excel để tính giá trị hiện tại ròng của một khoản đầu tư và cách tránh các lỗi thường gặp khi tính NPV trong Excel.

Giá trị hiện tại ròng hoặc giá trị hiện tại ròng là yếu tố cốt lõi của phân tích tài chính cho biết liệu một dự án có sinh lãi hay không. Tại sao giá trị hiện tại ròng lại quan trọng như vậy? Bởi vì khái niệm tài chính cơ bản cho rằng số tiền có thể nhận được trong tương lai có giá trị thấp hơn số tiền bạn có ngay bây giờ. Giá trị hiện tại ròng chiết khấu các dòng tiền dự kiến ​​trong tương lai về hiện tại để thể hiện giá trị hiện tại của chúng.

Microsoft Excel có một chức năng đặc biệt để tính NPV, nhưng việc sử dụng nó có thể phức tạp, đặc biệt đối với những người có ít kinh nghiệm trong mô hình tài chính. Mục đích của bài viết này là để cho bạn biết cách hoạt động của hàm NPV trong Excel và chỉ ra những cạm bẫy có thể xảy ra khi tính giá trị hiện tại ròng của một loạt dòng tiền trong Excel.

Ròng là gì giá trị hiện tại (NPV)?

Giá trị hiện tại ròng (NPV) là giá trị của một chuỗi các dòng tiền trong toàn bộ vòng đời của một dự án được chiết khấu về hiện tại.

Nói một cách đơn giản, NPV có thể được định nghĩa là giá trị hiện tại của dòng tiền trong tương lai trừ đi chi phí đầu tư ban đầu:

NPV = PV của dòng tiền trong tương lai – Đầu tư ban đầu

Để hiểu rõ hơn vềkhoảng thời gian có dòng tiền rỗng.

Tỷ lệ chiết khấu không tương ứng với khoảng thời gian thực tế

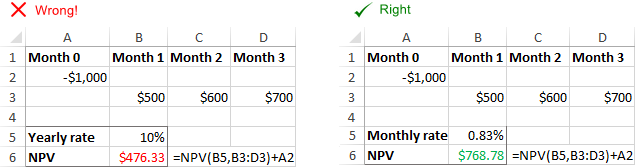
Hàm NPV của Excel không thể điều chỉnh tỷ lệ được cung cấp cho thời gian nhất định tần số tự động, ví dụ tỷ lệ chiết khấu hàng năm đối với dòng tiền hàng tháng. Người dùng có trách nhiệm cung cấp tỷ lệ thích hợp cho mỗi khoảng thời gian .

Định dạng tỷ lệ không chính xác

Mức chiết khấu hoặc lãi suất phải là được cung cấp dưới dạng tỷ lệ phần trăm hoặc số thập phân tương ứng. Ví dụ: tỷ lệ phần trăm 10 có thể được cung cấp dưới dạng 10% hoặc 0,1. Nếu bạn nhập tỷ lệ là số 10, Excel sẽ coi nó là 1000% và NPV sẽ bị tính sai.

Đó là cách sử dụng NPV trong Excel để tìm mạng giá trị hiện tại của một khoản đầu tư. Để xem kỹ hơn các công thức được thảo luận trong hướng dẫn này, vui lòng tải xuống công cụ tính NPV mẫu cho Excel của chúng tôi.

Cảm ơn bạn đã đọc và hy vọng được gặp bạn trên blog của chúng tôi vào tuần tới!

Đối với một dòng tiền duy nhất, giá trị hiện tại (PV) được tính theo công thức sau:

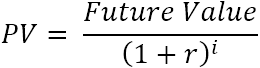
Ở đâu :

• r – chiết khấu hoặc lãi suất
• i – chu kỳ dòng tiền

Ví dụ: để nhận được $110 (giá trị tương lai) sau 1 năm (i), hôm nay bạn nên đầu tư bao nhiêu vào tài khoản ngân hàng đang có lãi suất 10%/năm (r)? Công thức trên đưa ra câu trả lời sau:

$110/(1+10%)^1 = $100

Nói cách khác, 100 đô la là giá trị hiện tại của 110 đô la dự kiến ​​sẽ nhận được trong tương lai.

Giá trị hiện tại ròng (NPV) cộng các giá trị hiện tại của tất cả các dòng tiền trong tương lai để đưa chúng về một điểm duy nhất trong hiện tại. Và bởi vì ý tưởng về "ròng" là cho thấy dự án sẽ sinh lời như thế nào sau khi hạch toán khoản đầu tư vốn ban đầu cần thiết để tài trợ cho dự án, số tiền đầu tư ban đầu được trừ vào tổng của tất cả các giá trị hiện tại:

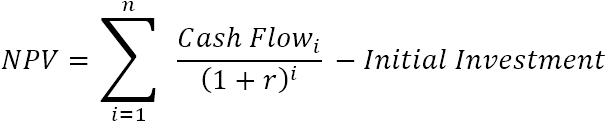
Trong đó:

• r – chiết khấu hoặc lãi suất
• n – số khoảng thời gian
• i – số lượng chu kỳ dòng tiền

Bởi vì bất kỳ số khác 0 nào được nâng lên lũy thừa 0 đều bằng 1, nên chúng ta có thể cộng khoản đầu tư ban đầu vào tổng. Xin lưu ý rằng trong phiên bản rút gọn này của công thức NPV, i=0, tức là khoản đầu tư ban đầu được thực hiện trong khoảng thời gian 0.

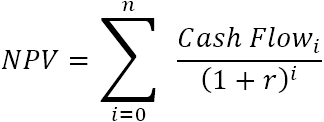
Ví dụ: để tìm NPV cho một dòng tiền (50, 60, 70) được chiết khấu 10% và chi phí ban đầu của$100, bạn có thể sử dụng công thức sau:

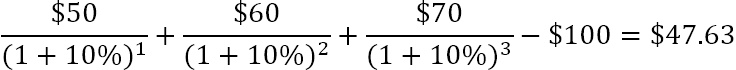
Hoặc

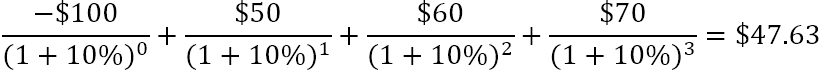
Giá trị hiện tại ròng giúp ích như thế nào trong việc đánh giá báo cáo tài chính tính khả thi của một khoản đầu tư được đề xuất? Giả định rằng một khoản đầu tư có NPV dương sẽ có lãi và một khoản đầu tư có NPV âm sẽ không có lãi. Khái niệm này là cơ sở của Quy tắc giá trị hiện tại ròng , quy tắc này nói rằng bạn chỉ nên tham gia vào các dự án có giá trị hiện tại ròng dương.

Hàm NPV trong Excel

Hàm Hàm NPV trong Excel trả về giá trị hiện tại ròng của một khoản đầu tư dựa trên chiết khấu hoặc lãi suất và một loạt các dòng tiền trong tương lai.

Cú pháp của hàm NPV trong Excel như sau:

Trong đó:

• Tỷ lệ (bắt buộc) - chiết khấu hoặc lãi suất trong một khoảng thời gian. Giá trị này phải được cung cấp dưới dạng phần trăm hoặc số thập phân tương ứng.
• Giá trị1, [giá trị2], … - giá trị số đại diện cho một chuỗi các dòng tiền thông thường. Giá trị1 là bắt buộc, các giá trị tiếp theo là tùy chọn. Trong các phiên bản hiện đại của Excel 2007 đến 2019, có thể cung cấp tối đa 254 đối số giá trị; trong Excel 2003 trở lên – lên tới 30 đối số.

Hàm NPV khả dụng trong Excel 365 - 2000.

Mẹo:

• Để tính toán giá trị hiện tại của niên kim, hãy sử dụng hàm PV trong Excel.
• Để ước tính lợi tức đầu tư dự kiến, hãy thực hiện phép tính IRR.

4 điều bạnnên biết về hàm NPV

Để đảm bảo rằng công thức NPV của bạn trong Excel tính toán chính xác, vui lòng lưu ý những điều sau:

• Các giá trị phải xuất hiện ở cuối mỗi kỳ . Nếu dòng tiền đầu tiên (khoản đầu tư ban đầu) xảy ra vào đầu kỳ đầu tiên , hãy sử dụng một trong các công thức NPV này.
• Các giá trị phải được cung cấp theo thứ tự thời gian và cách đều nhau về thời gian .
• Sử dụng các giá trị âm để biểu thị luồng chi (tiền đã chi) và giá trị dương để biểu thị luồng tiền vào (tiền nhận được ).
• Chỉ giá trị số được xử lý. Các ô trống, biểu thị văn bản của số, giá trị logic và giá trị lỗi bị bỏ qua.

Cách thức hoạt động của hàm NPV trong Excel

Việc sử dụng hàm NPV trong Excel hơi phức tạp vì cách chức năng được thực hiện. Theo mặc định, giả định rằng khoản đầu tư được thực hiện một khoảng thời gian trước ngày value1 . Vì lý do này, công thức NPV ở dạng thuần túy chỉ hoạt động đúng nếu bạn cung cấp chi phí đầu tư ban đầu trong một khoảng thời gian kể từ bây giờ , không phải hôm nay!

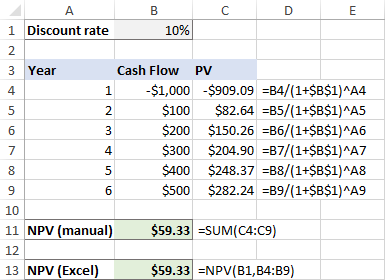
Để minh họa điều này, hãy tính giá trị hiện tại ròng theo cách thủ công và với công thức NPV của Excel, rồi so sánh kết quả.

Giả sử bạn có tỷ lệ chiết khấu trong B1, một chuỗi dòng tiền trong B4:B9 và số kỳ trong A4:A9.

Cung cấp các tham chiếu ở trên trong công thức PV chung này:

PV = tương laivalue/(1+rate)^period

Và bạn sẽ nhận được phương trình sau:

=B4/(1+$B$1)^A4

Công thức này chuyển đến C4 và sau đó được sao chép vào các ô bên dưới. Do sử dụng khéo léo các tham chiếu ô tuyệt đối và tương đối, công thức sẽ điều chỉnh hoàn hảo cho từng hàng như trong ảnh chụp màn hình bên dưới.

Xin lưu ý rằng chúng tôi cũng tính giá trị hiện tại của khoản đầu tư ban đầu vì chi phí đầu tư ban đầu là sau 1 năm , vì vậy nó cũng được chiết khấu.

Sau đó, chúng tôi tính tổng tất cả các giá trị hiện tại:

=SUM(C4:C9)

Và bây giờ, hãy làm NPV với hàm Excel:

=NPV(B1, B4:B9)

Như bạn có thể thấy, kết quả của cả hai phép tính khớp chính xác:

Nhưng sao nếu chi phí ban đầu xảy ra vào bắt đầu của giai đoạn đầu tiên , như thường xảy ra?

Bởi vì khoản đầu tư ban đầu được thực hiện ngay hôm nay, không áp dụng chiết khấu cho khoản đầu tư đó và chúng tôi chỉ cần thêm số tiền này thành tổng giá trị hiện tại của các dòng tiền trong tương lai (vì là số âm nên thực tế nó bị trừ):

=SUM(C4:C9)+B4

Và trong trường hợp này, tính toán thủ công và hàm NPV của Excel mang lại kết quả các kết quả khác nhau:

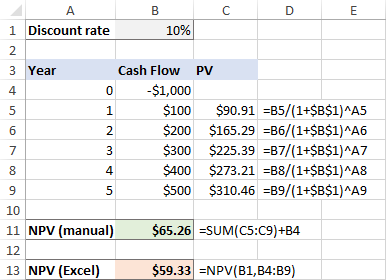
Điều này có nghĩa là chúng ta không thể dựa vào NPV để mula trong Excel và phải tính giá trị hiện tại ròng theo cách thủ công trong tình huống này? Dĩ nhiên là không! Bạn sẽ chỉ cần điều chỉnh hàm NPV một chút như được giải thích trong phần tiếp theo.

Cách tính NPV trong Excel

Khi đầu tư ban đầuđược thực hiện tại đầu kỳ đầu tiên , chúng ta có thể coi đó là dòng tiền vào cuối kỳ trước (tức là kỳ 0). Với ý nghĩ đó, có hai cách đơn giản để tìm NPV trong Excel.

Công thức NPV trong Excel 1

Không tính chi phí ban đầu trong phạm vi giá trị và trừ nó khỏi kết quả của hàm NPV . Vì kinh phí ban đầu thường được nhập dưới dạng số âm , nên bạn thực sự thực hiện thao tác cộng:

Trong trường hợp này, hàm NPV của Excel chỉ trả về giá trị hiện tại của các dòng tiền không đồng đều. Bởi vì chúng tôi muốn giá trị "ròng" (tức là giá trị hiện tại của dòng tiền trong tương lai trừ đi khoản đầu tư ban đầu), chúng tôi trừ đi chi phí ban đầu bên ngoài hàm NPV.

Công thức NPV Excel 2

Bao gồm chi phí ban đầu trong phạm vi giá trị và nhân kết quả với (1 + tỷ lệ).

Trong trường hợp này, hàm NPV của Excel sẽ cho bạn kết quả của giai đoạn -1 (như thể khoản đầu tư ban đầu được thực hiện trong một giai đoạn trước khoảng thời gian 0), chúng ta phải nhân sản lượng của nó với (1 + r) để đưa NPV về phía trước một khoảng thời gian (tức là từ i = -1 đến i = 0). Vui lòng xem dạng rút gọn của công thức NPV.

Việc sử dụng công thức nào là vấn đề sở thích cá nhân của bạn. Cá nhân tôi tin rằng cách đầu tiên đơn giản và dễ hiểu hơn.

Tính toán NPV trong Excel

Bây giờ hãy xem cách bạn có thể sử dụng cách trêncông thức trên dữ liệu thực để tạo máy tính NPV của riêng bạn trong Excel.

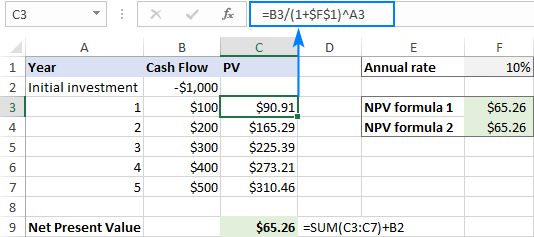
Giả sử bạn có chi phí ban đầu ở B2, một loạt các dòng tiền trong tương lai ở B3:B7 và tỷ lệ hoàn vốn bắt buộc ở F1. Để tìm NPV, hãy sử dụng một trong các công thức sau:

Công thức NPV 1:

=NPV(F1, B3:B7) + B2

Xin lưu ý rằng đối số giá trị đầu tiên là tiền mặt dòng chảy trong giai đoạn 1 (B3), chi phí ban đầu (B2) không được bao gồm.

NPV Công thức 2:

=NPV(F1, B2:B7) * (1+F1)

Công thức này bao gồm chi phí ban đầu (B2) trong phạm vi giá trị.

Ảnh chụp màn hình bên dưới hiển thị hoạt động của công cụ tính NPV trong Excel của chúng tôi:

Để đảm bảo NPV trong Excel của chúng tôi các công thức là chính xác, chúng ta hãy kiểm tra kết quả bằng các phép tính thủ công.

Đầu tiên, chúng ta tìm giá trị hiện tại của từng dòng tiền bằng cách sử dụng công thức PV đã thảo luận ở trên:

=B3/(1+$F$1)^A3

Tiếp theo, cộng tất cả các giá trị hiện tại và trừ đi chi phí đầu tư ban đầu:

=SUM(C3:C7)+B2

… và thấy rằng kết quả của cả ba công thức là hoàn toàn giống nhau.

Lưu ý. Trong ví dụ này, chúng ta đang xử lý dòng tiền hàng năm và lãi suất hàng năm. Nếu bạn muốn tìm NPV hàng quý hoặc hàng tháng trong Excel, hãy nhớ điều chỉnh tỷ lệ chiết khấu cho phù hợp như được giải thích trong ví dụ này.

Sự khác biệt giữa PV và NPV trong Excel

Trong tài chính, cả PV và NPV đều được sử dụng để đo lường giá trị hiện tại của dòng tiền trong tương lai bằng cách chiết khấu số tiền trong tương lai về hiện tại. Nhưng màchúng khác nhau ở một điểm quan trọng:

• Giá trị hiện tại (PV) - đề cập đến tất cả các dòng tiền vào trong tương lai trong một khoảng thời gian nhất định.
• Hiện tại ròng giá trị (NPV) – là chênh lệch giữa giá trị hiện tại của dòng tiền vào và giá trị hiện tại của dòng tiền ra.

Nói cách khác, PV chỉ hạch toán dòng tiền vào, còn NPV cũng hạch toán cho khoản đầu tư hoặc chi phí ban đầu, biến nó thành con số ròng.

Trong Microsoft Excel, có hai điểm khác biệt cơ bản giữa các hàm:

• Hàm NPV có thể tính toán (biến) không đồng đều dòng tiền. Chức năng PV yêu cầu dòng tiền không đổi trong suốt thời gian đầu tư.
• Với NPV, dòng tiền phải xuất hiện vào cuối mỗi kỳ. PV có thể xử lý các dòng tiền xảy ra vào cuối và đầu kỳ.

Sự khác biệt giữa NPV và XNPV trong Excel

XNPV là một hàm tài chính Excel khác dùng để tính toán giá trị hiện tại ròng của một khoản đầu tư. Sự khác biệt chính giữa các chức năng như sau:

• NPV coi tất cả các khoảng thời gian là bằng nhau .
• XNPV cho phép bạn chỉ định ngày tương ứng với từng khoảng thời gian dòng tiền. Vì lý do này, hàm XNPV chính xác hơn rất nhiều khi xử lý một loạt các dòng tiền ở các khoảng thời gian không đều đặn .

Không giống như NPV, hàm XNPV trong Excel được triển khai "bình thường " - giá trị đầu tiên tương ứng với dòng chảy ra xảy ra tạithời điểm bắt đầu đầu tư. Tất cả các dòng tiền liên tiếp được chiết khấu dựa trên một năm có 365 ngày.

Về mặt cú pháp, hàm XNPV có một đối số bổ sung:

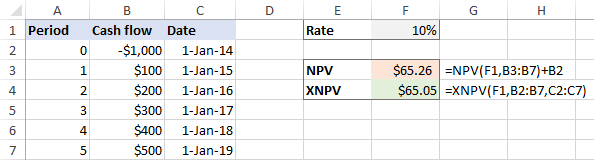
Ví dụ , hãy sử dụng cả hai hàm trên cùng một tập dữ liệu, trong đó F1 là tỷ lệ chiết khấu, B2:B7 là dòng tiền và C2:C7 là ngày:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Nếu dòng tiền được phân phối đồng đều thông qua khoản đầu tư, các hàm NPV và XNPV trả về các số liệu rất gần nhau:

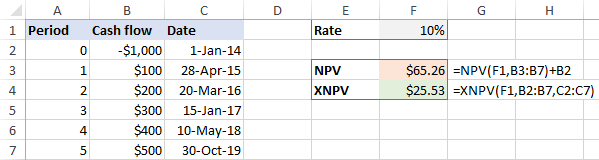
Trong trường hợp khoảng thời gian không đều , sự khác biệt giữa các kết quả là rất đáng kể:

Các lỗi thường gặp khi tính NPV trong Excel

Do cách thực hiện khá cụ thể của hàm NPV, nhiều lỗi xảy ra khi tính giá trị hiện tại ròng trong Excel. Các ví dụ đơn giản bên dưới minh họa các lỗi điển hình nhất và cách tránh chúng.

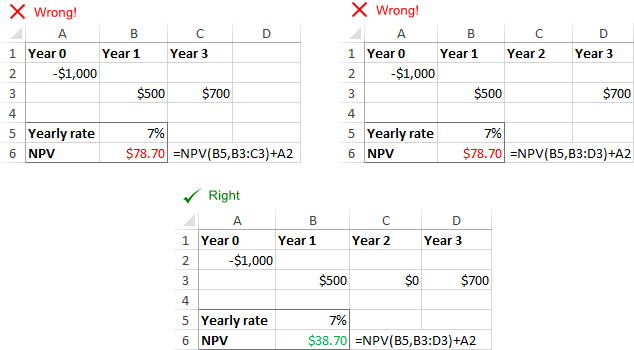
Khoảng thời gian không đều

Hàm NPV trong Excel giả định rằng tất cả các giai đoạn dòng tiền đều bằng nhau . Nếu bạn cung cấp các khoảng thời gian khác nhau, chẳng hạn như năm, quý hoặc tháng, giá trị hiện tại ròng sẽ không chính xác do các khoảng thời gian không nhất quán.

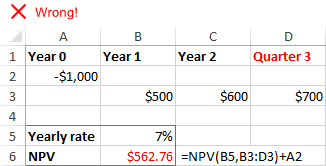
Thiếu các khoảng thời gian hoặc dòng tiền

NPV trong Excel không nhận ra các khoảng thời gian bị bỏ qua và bỏ qua các ô trống. Để tính toán NPV một cách chính xác, vui lòng đảm bảo cung cấp tháng, quý hoặc năm liên tiếp và cung cấp không giá trị cho thời gian