У овом водичу ћете научити како да користите Екцел НПВ функцију за израчунавање нето садашње вредности инвестиције и како да избегнете уобичајене грешке када радите НПВ у Екцел-у.

Нето садашња вредност или нето садашња вредност је кључни елемент финансијске анализе који показује да ли ће пројекат бити профитабилан или не. Зашто је нето садашња вредност толико важна? Зато што основни финансијски концепт сматра да новац који се потенцијално може примити у будућности вреди мање од исте количине новца коју тренутно имате. Нето садашња вредност дисконтује токове готовине који се очекују у будућности назад у садашњост да би показао њихову данашњу вредност.

Мицрософт Екцел има посебну функцију за израчунавање НПВ, али њена употреба може бити незгодна, посебно за људе који имају мало искуства у финансијском моделирању. Сврха овог чланка је да вам покаже како функционише Екцел НПВ функција и укаже на могуће замке приликом израчунавања нето садашње вредности низа новчаних токова у Екцел-у.

Шта је нето садашња вредност (НПВ)?

Нето садашња вредност (НПВ) је вредност низа новчаних токова током целог животног века пројекта дисконтована до садашњости.

Једноставно речено, НПВ се може дефинисати као садашња вредност будућих новчаних токова умањена за почетне трошкове улагања:

НПВ = ПВ будућих новчаних токова – почетна инвестиција

Да бисмо боље разумелипериоди који имају нулте токове готовине.

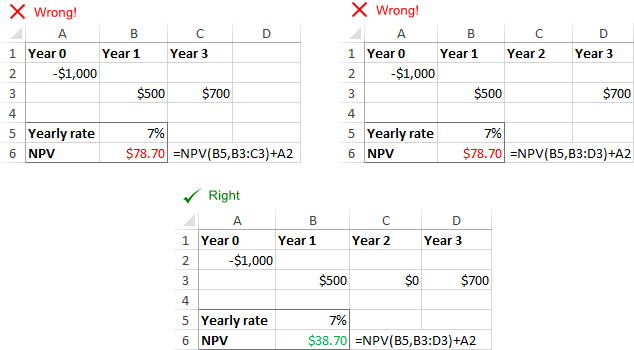
Стопа дисконтирања не одговара стварним временским периодима

Екцел функција НПВ не може да прилагоди испоручену стопу датом времену фреквенције аутоматски, на пример годишња дисконтована стопа на месечне токове готовине. Одговорност корисника је да обезбеди одговарајућу стопу по периоду .

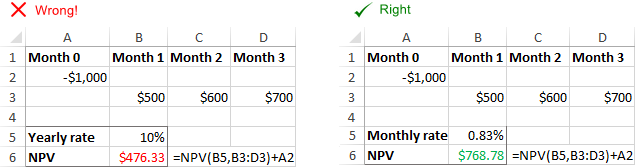
Нетачан формат стопе

Попуст или каматна стопа морају бити дато као проценат или одговарајући децимални број . На пример, стопа од 10 процената се може доставити као 10% или 0,1. Ако унесете стопу као број 10, Екцел ће је третирати као 1000%, а НПВ ће бити погрешно израчунат.

Тако се користи НПВ у Екцел-у да бисте пронашли нето садашња вредност инвестиције. Да бисте ближе погледали формуле о којима се говори у овом водичу, слободно преузмите наш пример калкулатора НПВ за Екцел.

Хвала вам на читању и надамо се да се видимо на нашем блогу следеће недеље!

За један новчани ток, садашња вредност (ПВ) се израчунава са овом формулом:

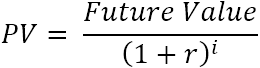
Где :

• р – дисконт или каматна стопа
• и – период тока готовине

На пример, да добијете 110 УСД (будућа вредност) након 1 године (и), колико бисте данас требали уложити на свој банковни рачун који нуди 10% годишње каматне стопе (р)? Горња формула даје овај одговор:

$110/(1+10%)^1 = $100

Другим речима, 100 долара је садашња вредност од 110 долара за које се очекује да ће бити примљени у будућности.

Нето садашња вредност (НПВ) сабира садашње вредности свих будућих новчаних токова како би их довео до једне тачке у садашњости. И пошто је идеја „нето“ да покаже колико ће пројекат бити профитабилан након што се урачунају почетна капитална улагања потребна за финансирање, износ почетне инвестиције се одузима од збира свих садашњих вредности:

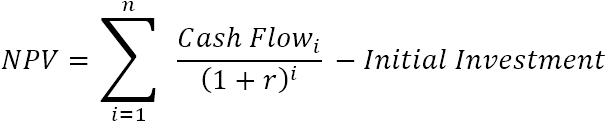
Где је:

• р – дисконтна или каматна стопа
• н – број временских периода
• и – период новчаног тока

Пошто је било који број различит од нуле подигнут на нулти степен једнак 1, можемо укључити почетно улагање у збир. Имајте на уму да је у овој компактној верзији формуле НПВ и=0, тј. почетно улагање се врши у периоду 0.

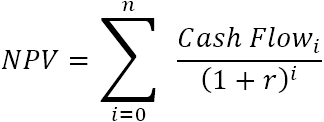
На пример, да бисте пронашли НПВ за серија новчаних токова (50, 60, 70) дисконтованих на 10% и почетни трошак100 долара, можете користити ову формулу:

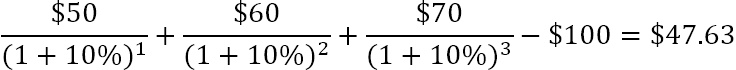
Или

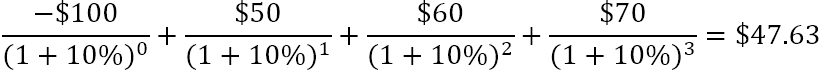
Како нето садашња вредност помаже у процени финансијског одрживост предложене инвестиције? Претпоставља се да ће инвестиција са позитивном НПВ бити профитабилна, а инвестиција са негативном НПВ бити непрофитабилна. Овај концепт је основа Правила нето садашње вредности , које каже да треба да се бавите само пројектима са позитивном нето садашњом вредношћу.

Екцел функција НПВ

Функција НПВ у Екцел-у враћа нето садашњу вредност инвестиције засновану на дисконтној или каматној стопи и низу будућих токова готовине.

Синтакса функције Екцел НПВ је следећа:

Где:

• Стопа (обавезно) - дисконт или каматна стопа током једног периода. Мора се навести као проценат или одговарајући децимални број.
• Вредност1, [вредност2], … - нумеричке вредности које представљају низ редовних новчаних токова. Вредност1 је обавезна, следеће вредности су опционе. У модерним верзијама програма Екцел 2007 до 2019, могу се доставити до 254 аргумента вредности; у програму Екцел 2003 и старијим – до 30 аргумената.

Функција НПВ је доступна у програму Екцел 365 - 2000.

Савети:

• За израчунавање садашњу вредност ануитета, користите Екцел ПВ функцију.
• Да бисте проценили пројектовани повраћај инвестиције, урадите прорачун ИРР-а.

4 ствари којетреба да знате о функцији НПВ

Да бисте осигурали да се ваша формула НПВ у Екцел-у правилно израчунава, имајте на уму ове чињенице:

• Вредности се морају појавити на крају сваког периода . Ако се први новчани ток (почетна инвестиција) догоди на почетку првог периода , користите једну од ових формула НПВ.
• Вредности морају бити наведене хронолошким редоследом и подједнако распоређене у времену .
• Користите негативне вредности за представљање одлива (готовина исплаћена) и позитивне вредности за представљање прилива (готовина примљена ).
• Обрађују се само нумеричке вредности . Празне ћелије, текстуални прикази бројева, логичких вредности и вредности грешака се занемарују.

Како функционише Екцел НПВ функција

Коришћење функције НПВ у Екцел-у је мало незгодно због начин на који се функција имплементира. Подразумевано, претпоставља се да је инвестиција извршена један период пре датума валуе1 . Из тог разлога, формула НПВ у свом чистом облику функционише исправно само ако наведете почетне трошкове улагања један период од сада , а не данас!

Да бисмо ово илустровали, хајде да израчунамо нето садашњу вредност ручно и помоћу Екцел формуле НПВ и упоредите резултате.

Рецимо, имате дисконтну стопу у Б1, низ токова готовине у Б4:Б9 и бројеве периода у А4:А9.

Наведите горе наведене референце у овој генеричкој ПВ формули:

ПВ = будућноствредност/(1+стопа)^период

И добићете следећу једначину:

=B4/(1+$B$1)^A4

Ова формула иде у Ц4 и затим се копира у ћелије испод. Због паметне употребе апсолутних и релативних референци ћелија, формула се савршено прилагођава за сваки ред као што је приказано на снимку екрана испод.

Имајте на уму да ми израчунавамо и садашњу вредност почетне инвестиције од почетне цене инвестиције је после 1 године , тако да је и снижено.

Након тога збројимо све садашње вредности:

=SUM(C4:C9)

А сада, хајде да урадите НПВ са Екцел функцијом:

=NPV(B1, B4:B9)

Као што видите, резултати оба прорачуна се тачно поклапају:

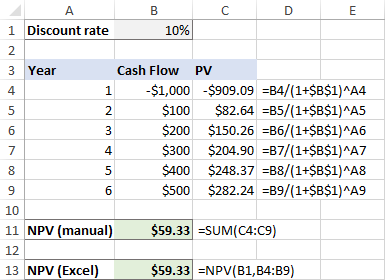
Али шта ако се почетни издатак деси на почетку првог периода , као што се обично дешава?

Пошто је почетна инвестиција направљена данас, на њу се не примењује никакав попуст, а ми једноставно додамо овај износ на збир садашњих вредности будућих новчаних токова (пошто је негативан број, заправо се одузима):

=SUM(C4:C9)+B4

И у овом случају, ручно израчунавање и Екцел НПВ функција приноса различити резултати:

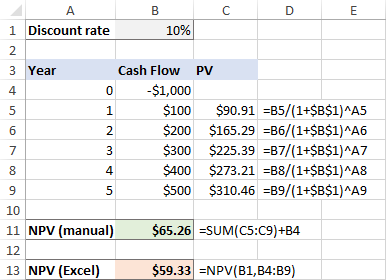
Да ли то значи да се не можемо ослонити на НПВ за мула у Екцел-у и морате ручно израчунати нето садашњу вредност у овој ситуацији? Наравно да не! Мораћете само мало да подесите НПВ функцију као што је објашњено у следећем одељку.

Како израчунати НПВ у Екцел-у

Када је почетна инвестицијаје направљен на почетку првог периода , можемо га третирати као новчани ток на крају претходног периода (тј. период 0). Имајући то на уму, постоје два једноставна начина да пронађете НПВ у Екцел-у.

Екцел НПВ формула 1

Оставите почетни трошак ван опсега вредности и одузмите га од резултата функције НПВ . Пошто се почетни издатак обично уноси као негативан број , ви заправо изводите операцију сабирања:

У овом случају, Екцел НПВ функција само враћа садашња вредност неуједначених новчаних токова. Пошто желимо „нето“ (тј. садашњу вредност будућих новчаних токова умањену за почетну инвестицију), одузимамо почетни трошак изван функције НПВ.

Екцел формула НПВ 2

Укључи почетну цену у опсегу вредности и помножите резултат са (1 + стопа).

У овом случају, Екцел НПВ функција би вам дала резултат од периода -1 (као да је почетна инвестиција извршена један период пре периода 0), морамо да помножимо његов излаз са (1 + р) да бисмо НПВ померили унапред за један временски период (тј. од и = -1 до и = 0). Молимо погледајте компактни облик формуле НПВ.

Коју формулу ћете користити је ствар ваших личних преференција. Лично верујем да је први једноставнији и лакши за разумевање.

калкулатор НПВ у Екцел-у

Сада да видимо како можете да користите горенаведеноформуле на стварним подацима да направите сопствени калкулатор НПВ у Екцел-у.

Претпоставимо да имате почетни издатак у Б2, низ будућих токова готовине у Б3:Б7 и потребну стопу поврата у Ф1. Да бисте пронашли НПВ, користите једну од следећих формула:

НПВ формула 1:

=NPV(F1, B3:B7) + B2

Имајте у виду да је први аргумент вредности готовина проток у периоду 1 (Б3), почетни трошак (Б2) није укључен.

НПВ Формула 2:

=NPV(F1, B2:B7) * (1+F1)

Ова формула укључује почетни трошак (Б2) у опсегу вредности.

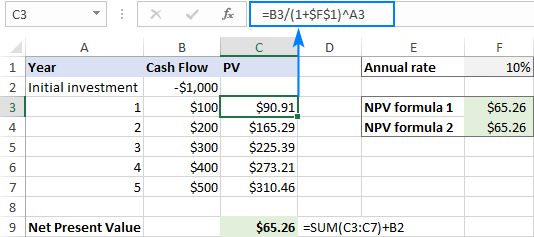
Снимак екрана испод приказује наш Екцел НПВ калкулатор у акцији:

Да бисмо били сигурни да је наш Екцел НПВ формуле су тачне, хајде да проверимо резултат ручним прорачунима.

Прво, налазимо садашњу вредност сваког новчаног тока користећи ПВ формулу о којој смо горе говорили:

=B3/(1+$F$1)^A3

Даље, саберите све садашње вредности и одузмите почетни трошак инвестиције:

=SUM(C3:C7)+B2

… и видите да су резултати све три формуле апсолутно исти.

Напомена. У овом примеру имамо посла са годишњим новчаним токовима и годишњом стопом. Ако желите да пронађете кварталну или месечну НПВ у Екцел-у, обавезно прилагодите дисконтну стопу у складу с тим како је објашњено у овом примеру.

Разлика између ПВ и НПВ у Екцел

У финансијама, и ПВ и НПВ се користе за мерење тренутне вредности будућих новчаних токова дисконтовањем будућих износа на садашње. Алиразликују се на један важан начин:

• Садашња вредност (ПВ) – односи се на све будуће приливе готовине у датом периоду.
• Нето садашња вредност (НПВ) – је разлика између садашње вредности прилива готовине и садашње вредности одлива готовине.

Другим речима, ПВ обрачунава само приливе готовине, док НПВ такође рачуна за почетну инвестицију или издатак, чинећи то нето цифром.

У Мицрософт Екцел-у постоје две суштинске разлике између функција:

• Функција НПВ може израчунати неуједначено (променљиво) готовински токови. Функција ПВ захтева да новчани токови буду константни током целог века улагања.
• Код НПВ, токови готовине морају да се јављају на крају сваког периода. ПВ може да управља новчаним токовима који се јављају на крају и на почетку периода.

Разлика између НПВ и КСНПВ у Екцел-у

КСНПВ је још једна Екцел финансијска функција која израчунава нето садашња вредност инвестиције. Основна разлика између функција је следећа:

• НПВ сматра да су сви временски периоди једнаки .
• КСНПВ вам омогућава да наведете датуме који одговарају сваком проток новца. Из тог разлога, КСНПВ функција је много прецизнија када се бави низом новчаних токова у неправилним интервалима .

За разлику од НПВ, Екцел КСНПВ функција се имплементира „нормално " - прва вредност одговара одливу који се јавља напочетак инвестиције. Сви узастопни токови готовине се дисконтују на основу године од 365 дана.

У смислу синтаксе, КСНПВ функција има један додатни аргумент:

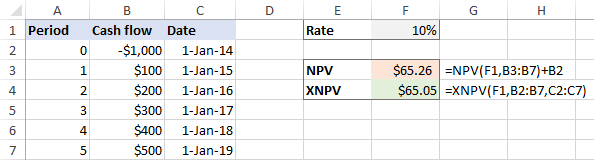
Као пример , хајде да користимо обе функције на истом скупу података, где је Ф1 дисконтна стопа, Б2:Б7 су токови готовине и Ц2:Ц7 су датуми:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Ако су токови готовине распоређени равномерно кроз инвестицију, функције НПВ и КСНПВ враћају веома блиске бројке:

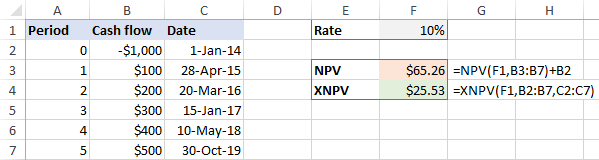
У у случају неправилних интервала , разлика између резултата је веома значајна:

Уобичајене грешке при израчунавању НПВ у Екцел-у

Због прилично специфична имплементација НПВ функције, праве се многе грешке приликом израчунавања нето садашње вредности у Екцел-у. Једноставни примери у наставку показују најчешће грешке и како их избећи.

Неправилни интервали

Екцел функција НПВ претпоставља да су сви периоди тока готовине једнаки . Ако наведете различите интервале, рецимо године и квартале или месеце, нето садашња вредност ће бити нетачна због некохерентних временских периода.

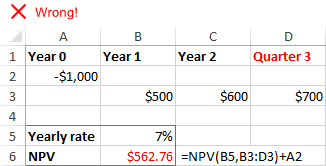
Недостају периоди или токови готовине

НПВ у Екцел-у не препознаје изостављене тачке и игнорише празне ћелије. Да бисте исправно израчунали НПВ, обавезно наведите узастопних месеци, квартала или година и наведите нула вредности за време