W tym tutorialu dowiesz się, jak używać funkcji NPV w Excelu, aby obliczyć wartość bieżącą netto inwestycji i jak uniknąć częstych błędów podczas wykonywania NPV w Excelu.

Wartość bieżąca netto lub wartość bieżąca netto jest podstawowym elementem analizy finansowej, który wskazuje, czy projekt będzie opłacalny, czy nie. Dlaczego wartość bieżąca netto jest tak ważna? Ponieważ podstawowa koncepcja finansowa mówi, że pieniądze, które potencjalnie można otrzymać w przyszłości, są warte mniej niż ta sama kwota pieniędzy, którą mamy teraz. Wartość bieżąca netto dyskontuje przepływy pieniężne oczekiwane w przyszłości z powrotem do teraźniejszościby pokazać swoją dzisiejszą wartość.

Microsoft Excel ma specjalną funkcję do obliczania NPV, ale jej użycie może być podstępne, zwłaszcza dla osób, które mają niewielkie doświadczenie w modelowaniu finansowym. Celem tego artykułu jest pokazanie, jak działa funkcja NPV w Excelu i wskazanie możliwych pułapek podczas obliczania wartości bieżącej netto serii przepływów pieniężnych w Excelu.

Co to jest wartość bieżąca netto (NPV)?

Wartość bieżąca netto (NPV) to wartość serii przepływów pieniężnych w całym okresie życia projektu zdyskontowana do dnia dzisiejszego.

W uproszczeniu NPV można zdefiniować jako wartość bieżącą przyszłych przepływów pieniężnych pomniejszoną o początkowy koszt inwestycji:

NPV = PV przyszłych przepływów pieniężnych - Inwestycja początkowa

Aby lepiej zrozumieć ten pomysł, zagłębmy się nieco w matematykę.

Dla pojedynczego przepływu pieniężnego wartość bieżącą (PV) oblicza się za pomocą tego wzoru:

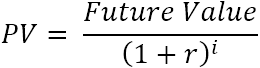
Gdzie:

• r - stopa dyskontowa lub procentowa
• i - okres przepływu środków pieniężnych

Na przykład, aby uzyskać 110 dolarów (wartość przyszła) po 1 roku (i), ile powinieneś zainwestować dzisiaj na koncie bankowym, które oferuje 10% roczną stopę procentową (r)? Powyższy wzór daje taką odpowiedź:

$110/(1+10%)^1 = $100

Innymi słowy, 100$ to wartość bieżąca 110$, które mają wpłynąć w przyszłości.

Wartość bieżąca netto (NPV) sumuje wartości bieżące wszystkich przyszłych przepływów pieniężnych, aby doprowadzić je do jednego punktu w teraźniejszości. A ponieważ ideą słowa "netto" jest pokazanie, jak opłacalny będzie projekt po uwzględnieniu początkowej inwestycji kapitałowej wymaganej do jego sfinansowania, kwota początkowej inwestycji jest odejmowana od sumy wszystkich wartości bieżących:

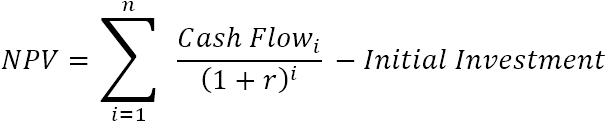
Gdzie:

• r - stopa dyskontowa lub procentowa
• n - liczba okresów czasu
• i - okres przepływu środków pieniężnych

Ponieważ każda niezerowa liczba podniesiona do potęgi zero równa się 1, możemy w tej sumie uwzględnić inwestycję początkową. Zauważmy, że w tej kompaktowej wersji wzoru NPV, i=0, czyli inwestycja początkowa jest dokonywana w okresie 0.

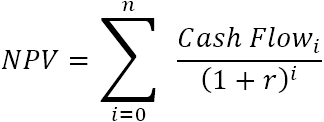
Na przykład, aby znaleźć NPV dla serii przepływów pieniężnych (50, 60, 70) zdyskontowanych przy 10% i koszcie początkowym 100$, można użyć tego wzoru:

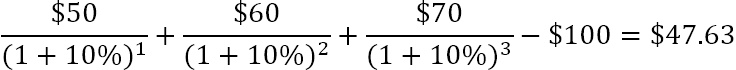
Lub

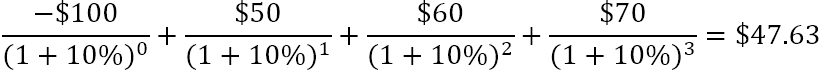
Jak wartość bieżąca netto pomaga w ocenie opłacalności finansowej proponowanej inwestycji? Przyjmuje się, że inwestycja o dodatniej NPV będzie opłacalna, a inwestycja o ujemnej NPV będzie nieopłacalna.Koncepcja ta jest podstawą Zasada wartości bieżącej netto , który mówi, że należy angażować się tylko w projekty o dodatniej wartości bieżącej netto.

Funkcja NPV w programie Excel

Funkcja NPV w programie Excel zwraca wartość bieżącą netto inwestycji na podstawie stopy dyskontowej lub procentowej oraz serii przyszłych przepływów pieniężnych.

Składnia funkcji NPV w Excelu jest następująca:

Gdzie:

• Stawka (wymagane) - stopa dyskontowa lub procentowa w jednym okresie. Musi być podana jako procent lub odpowiednia liczba dziesiętna.
• Wartość1, [wartość2], ... - wartości liczbowe reprezentujące serię regularnych przepływów pieniężnych. Wartość1 jest wymagana, kolejne wartości są opcjonalne. W nowoczesnych wersjach Excela od 2007 do 2019 można podać do 254 argumentów wartości; w Excelu 2003 i starszych - do 30 argumentów.

Funkcja NPV jest dostępna w programie Excel 365 - 2000.

Wskazówki:

• Aby obliczyć wartość bieżącą renty, należy użyć funkcji PV programu Excel.
• Aby oszacować przewidywany zwrot z inwestycji, wykonaj obliczenia IRR.

4 rzeczy, które powinieneś wiedzieć o funkcji NPV

Aby upewnić się, że Twoja formuła NPV w Excelu oblicza poprawnie, pamiętaj o tych faktach:

• Wartości muszą wystąpić w koniec każdego okresu Jeżeli pierwszy przepływ środków pieniężnych (inwestycja początkowa) następuje w momencie początek pierwszego okresu , użyj jednego z tych wzorów NPV.
• Wartości muszą być podane w porządek chronologiczny oraz równo rozłożone w czasie .
• Użyj negatywny wartości reprezentujące wypływy (wypłacone środki pieniężne) i pozytywny wartości reprezentujące wpływy (otrzymane środki pieniężne).
• Tylko wartości numeryczne Puste komórki, tekstowe reprezentacje liczb, wartości logiczne i wartości błędów są ignorowane.

Jak działa funkcja NPV w Excelu

Korzystanie z funkcji NPV w Excelu jest nieco kłopotliwe ze względu na sposób implementacji funkcji. Domyślnie zakłada się, że inwestycja jest dokonywana na jeden okres przed wartość1 Z tego powodu wzór NPV w czystej postaci działa poprawnie tylko wtedy, gdy podamy początkowy koszt inwestycji za jeden okres od teraz nie dzisiaj!

Aby to zilustrować, obliczmy wartość bieżącą netto ręcznie oraz za pomocą formuły NPV w Excelu i porównajmy wyniki.

Załóżmy, że masz stopę dyskontową w B1, serię przepływów pieniężnych w B4:B9 i numery okresów w A4:A9.

Dostarcz powyższe referencje w tej ogólnej formule PV:

PV = wartość przyszła/(1+stopa)^okres

I otrzymamy następujące równanie:

=B4/(1+$B$1)^A4

Ta formuła trafia do C4, a następnie jest kopiowana do poniższych komórek. Dzięki sprytnemu użyciu bezwzględnych i względnych odniesień do komórek formuła doskonale dostosowuje się do każdego wiersza, jak pokazano na poniższym zrzucie ekranu.

Proszę zauważyć, że obliczamy również wartość bieżącą inwestycji początkowej, ponieważ koszt inwestycji początkowej wynosi po 1 roku , więc jest to również dyskontowane.

Następnie sumujemy wszystkie obecne wartości:

=SUM(C4:C9)

A teraz zróbmy NPV za pomocą funkcji w Excelu:

=NPV(B1, B4:B9)

Jak widać, wyniki obu obliczeń dokładnie się zgadzają:

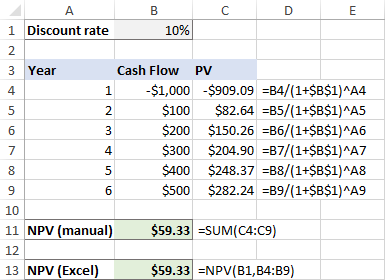
Ale co w sytuacji, gdy początkowy nakład pojawia się przy. początek pierwszego okresu jak to zwykle bywa?

Ponieważ inwestycja początkowa jest dokonywana dzisiaj, nie stosuje się do niej dyskontowania i po prostu dodajemy tę kwotę do sumy wartości bieżących przyszłych przepływów pieniężnych (ponieważ jest to liczba ujemna, jest ona w rzeczywistości odejmowana):

=SUM(C4:C9)+B4

I w tym przypadku ręczne obliczenia i funkcja NPV Excela dają różne wyniki:

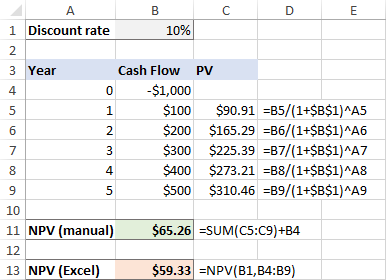
Czy to oznacza, że nie możemy polegać na formule NPV w Excelu i musimy w tej sytuacji obliczać wartość bieżącą netto ręcznie? Oczywiście, że nie! Trzeba będzie tylko nieco podrasować funkcję NPV, jak wyjaśniono w następnym rozdziale.

Jak obliczyć NPV w programie Excel

Gdy inwestycja początkowa jest realizowana na początek pierwszego okresu , możemy potraktować go jako przepływ pieniężny na koniec poprzedniego okresu (czyli okresu 0). Mając to na uwadze, istnieją dwa proste sposoby znalezienia NPV w Excelu.

Wzór NPV w Excelu 1

Pozostawienie kosztu początkowego poza zakresem wartości i odjęcie go od wyniku funkcji NPV.Ponieważ nakład początkowy jest zwykle wpisywany jako liczba ujemna , faktycznie wykonujesz operację dodawania:

W tym przypadku funkcja NPV Excela zwraca po prostu wartość bieżącą nierównych przepływów pieniężnych. Ponieważ chcemy "netto" (tj. wartość bieżącą przyszłych przepływów pieniężnych pomniejszoną o inwestycję początkową), odejmujemy koszt początkowy poza funkcją NPV.

Wzór NPV w Excelu 2

Uwzględnij koszt początkowy w zakresie wartości i pomnóż wynik przez (1 + stawka).

W tym przypadku funkcja NPV Excela podałaby wynik na okres -1 (tak jakby inwestycja początkowa została dokonana jeden okres przed okresem 0), musimy pomnożyć jej wynik przez (1 + r), aby przenieść NPV o jeden okres do przodu (czyli z i = -1 do i = 0). Proszę zobaczyć zwartą formę formuły NPV.

To, której formuły użyć, jest kwestią twoich osobistych preferencji. Osobiście uważam, że pierwsza jest prostsza i łatwiejsza do zrozumienia.

Kalkulator NPV w Excelu

Teraz zobaczmy, jak można użyć powyższych formuł na rzeczywistych danych, aby stworzyć własny kalkulator NPV w Excelu.

Załóżmy, że masz początkowy nakład w B2, serię przyszłych przepływów pieniężnych w B3:B7 oraz wymaganą stopę zwrotu w F1. Aby znaleźć NPV, użyj jednego z następujących wzorów:

Wzór NPV 1:

=NPV(F1, B3:B7) + B2

Proszę zauważyć, że pierwszym argumentem wartości jest przepływ pieniężny w okresie 1 (B3), koszt początkowy (B2) nie jest uwzględniony.

NPV Wzór 2:

=NPV(F1, B2:B7) * (1+F1)

Wzór ten uwzględnia w zakresie wartości koszt początkowy (B2).

Poniższy zrzut ekranu pokazuje nasz kalkulator NPV w Excelu w akcji:

Aby upewnić się, że nasze formuły NPV w Excelu są poprawne, sprawdźmy wynik za pomocą ręcznych obliczeń.

Najpierw znajdujemy wartość bieżącą każdego przepływu pieniężnego, korzystając z omówionego powyżej wzoru PV:

=B3/(1+$F$1)^A3

Następnie zsumuj wszystkie wartości bieżące i odejmij początkowy koszt inwestycji:

=SUM(C3:C7)+B2

... i zobaczyć, że wyniki wszystkich trzech formuł są absolutnie takie same.

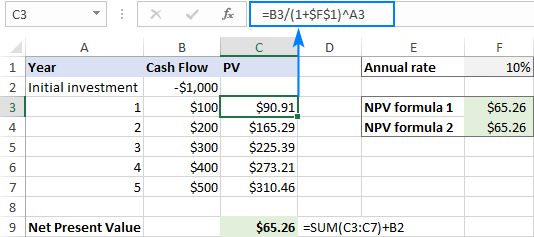
Uwaga. W tym przykładzie mamy do czynienia z rocznymi przepływami pieniężnymi i roczną stopą procentową. Jeśli mamy znaleźć kwartalnik lub miesięcznie NPV w Excelu, pamiętaj, aby odpowiednio dostosować stopę dyskontową, jak wyjaśniono w tym przykładzie.

Różnica między PV a NPV w Excelu

W finansach, zarówno PV jak i NPV są używane do pomiaru bieżącej wartości przyszłych przepływów pieniężnych poprzez dyskontowanie przyszłych kwot do teraźniejszości. Różnią się one jednak w jeden ważny sposób:

• Wartość bieżąca (PV) - odnosi się do wszystkich przyszłych wpływów pieniężnych w danym okresie.
• Wartość bieżąca netto (NPV) - jest różnicą pomiędzy wartością bieżącą wpływów pieniężnych a wartością bieżącą wypływów pieniężnych.

Innymi słowy, PV uwzględnia jedynie wpływy pieniężne, podczas gdy NPV uwzględnia również początkową inwestycję lub nakłady, co czyni ją wartością netto.

W programie Microsoft Excel istnieją dwie zasadnicze różnice między funkcjami:

• Funkcja NPV może obliczać nierównomierne (zmienne) przepływy pieniężne. Funkcja PV wymaga, aby przepływy pieniężne były stałe przez cały okres trwania inwestycji.
• W przypadku NPV przepływy pieniężne muszą wystąpić na koniec każdego okresu. PV może obsługiwać przepływy pieniężne, które występują na końcu i na początku okresu.

Różnica między NPV a XNPV w Excelu

XNPV to jeszcze jedna funkcja finansowa Excela, która oblicza wartość bieżącą netto inwestycji. Podstawowa różnica między tymi funkcjami jest następująca:

• NPV uznaje wszystkie okresy czasu za równe .
• XNPV pozwala na określenie dat, które odpowiadają każdemu przepływowi pieniężnemu. Z tego powodu funkcja XNPV jest o wiele bardziej precyzyjna, gdy mamy do czynienia z serią przepływów pieniężnych przy nieregularne odstępy .

W przeciwieństwie do NPV, funkcja XNPV w Excelu jest realizowana "normalnie" - pierwsza wartość odpowiada wypływowi, który występuje na początku inwestycji. Wszystkie kolejne przepływy pieniężne są dyskontowane w oparciu o rok 365-dniowy.

Pod względem składniowym funkcja XNPV ma jeden dodatkowy argument:

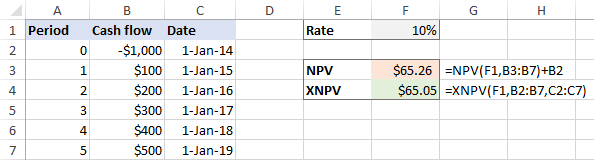
Jako przykład użyjmy obu funkcji na tym samym zestawie danych, gdzie F1 to stopa dyskontowa, B2:B7 to przepływy pieniężne, a C2:C7 to daty:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Jeżeli przepływy pieniężne są rozprowadzane równomiernie przez inwestycję, funkcje NPV i XNPV zwracają bardzo zbliżone wartości:

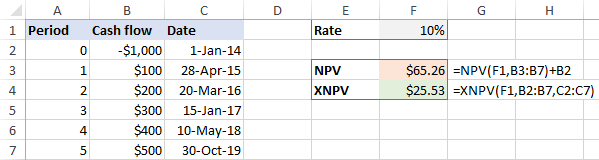
W przypadku nieregularne odstępy , różnica między wynikami jest bardzo znacząca:

Częste błędy przy obliczaniu NPV w Excelu

Ze względu na dość specyficzną implementację funkcji NPV, podczas obliczania wartości bieżącej netto w Excelu popełnianych jest wiele błędów. Poniższe proste przykłady pokazują najbardziej typowe błędy i jak ich unikać.

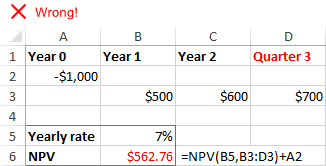
Nieregularne odstępy czasu

Funkcja NPV programu Excel zakłada, że wszystkie okresy przepływów pieniężnych są równe Jeśli podasz różne przedziały czasowe, powiedzmy lata i kwartały lub miesiące, wartość bieżąca netto będzie nieprawidłowa ze względu na niespójne okresy czasu.

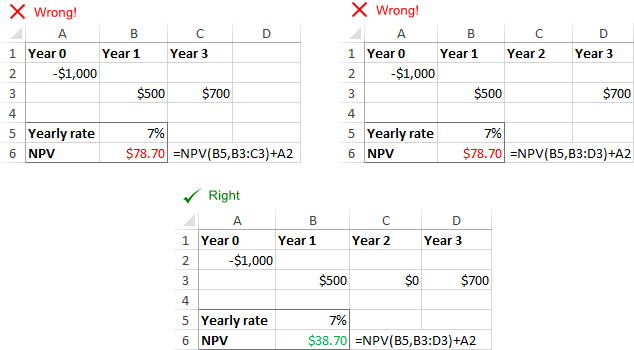
Brakujące okresy lub przepływy pieniężne

NPV w Excelu nie rozpoznaje pominiętych okresów i ignoruje puste komórki. Aby poprawnie obliczyć NPV, należy podać kolejny miesięcy, kwartałów lub lat oraz dostaw zero wartości dla okresów czasu, które mają zerowe przepływy pieniężne.

Stopa dyskontowa nie odpowiada rzeczywistym okresom czasu

Funkcja NPV programu Excel nie może automatycznie dopasować dostarczonej stopy do podanych częstotliwości czasowych, np. rocznej stopy dyskontowej do miesięcznych przepływów pieniężnych.Obowiązkiem użytkownika jest dostarczenie właściwa stawka za okres .

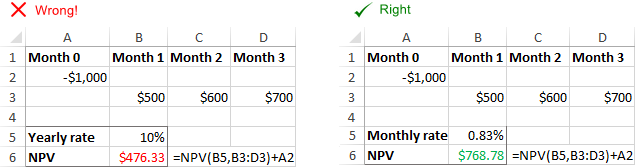
Nieprawidłowy format stawki

Dyskonto lub stopa procentowa musi być podana jako procent lub odpowiadający liczba dziesiętna . Na przykład stopa 10% może być dostarczona jako 10% lub 0,1. Jeśli wpiszesz stopę jako liczbę 10, Excel potraktuje ją jako 1000% i NPV zostanie obliczone źle.

Oto jak wykorzystać NPV w Excelu, aby znaleźć wartość bieżącą netto inwestycji. Aby przyjrzeć się bliżej formułom omawianym w tym tutorialu, zapraszamy do pobrania naszego przykładowego kalkulatora NPV dla Excela.

Dziękujemy za przeczytanie i mamy nadzieję, że zobaczymy się na naszym blogu za tydzień!