Ebben a bemutatóban megtanulhatja, hogyan használja az Excel NPV funkcióját egy befektetés nettó jelenértékének kiszámításához, és hogyan kerülheti el a gyakori hibákat, amikor az NPV-t Excelben végzi.

Nettó jelenérték vagy nettó jelenérték a pénzügyi elemzés egyik központi eleme, amely megmutatja, hogy egy projekt nyereséges lesz-e vagy sem. Miért olyan fontos a nettó jelenérték? Mert az alapvető pénzügyi koncepció szerint a jövőben potenciálisan megkapható pénz kevesebbet ér, mint ugyanannyi pénz, amivel most rendelkezünk. A nettó jelenérték a jövőben várható pénzáramlásokat visszadiszkontálja a jelenre.hogy megmutassák mai értéküket.

A Microsoft Excel rendelkezik egy speciális funkcióval az NPV kiszámítására, de használata trükkös lehet, különösen azok számára, akiknek kevés tapasztalatuk van a pénzügyi modellezésben. E cikk célja, hogy bemutassa, hogyan működik az Excel NPV funkciója, és rámutasson a lehetséges buktatókra, amikor egy pénzáramlási sorozat nettó jelenértékét számítja ki Excelben.

Mi a nettó jelenérték (NPV)?

Nettó jelenérték (NPV) a projekt teljes élettartama alatt a pénzáramlások sorozatának a jelenre diszkontált értéke.

Egyszerűen fogalmazva, az NPV a jövőbeli pénzáramlások jelenértékeként határozható meg, csökkentve a kezdeti beruházási költséggel:

NPV = a jövőbeli pénzáramlások PV-je - Kezdeti befektetés

Hogy jobban megértsük az ötletet, ássunk egy kicsit mélyebbre a matematikában.

Egyetlen pénzáram esetén a jelenértéket (PV) ezzel a képlettel számítják ki:

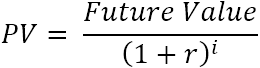
Hol:

• r - diszkont vagy kamatláb
• i - a pénzforgalmi időszak

Például ahhoz, hogy 1 év múlva 110 dollárhoz (jövőbeli érték) jusson (i), mennyit kellene ma befektetnie a 10%-os éves kamatlábat kínáló bankszámlájára (r)? A fenti képlet ezt a választ adja:

$110/(1+10%)^1 = $100

Más szóval, 100 dollár a jövőben várhatóan befolyó 110 dollár jelenértéke.

A nettó jelenérték (NPV) összeadja az összes jövőbeli pénzáramlás jelenértékét, hogy azokat egyetlen pontba hozza a jelenben. És mivel a "nettó" lényege, hogy megmutassa, mennyire lesz nyereséges a projekt a finanszírozásához szükséges kezdeti tőkebefektetés elszámolása után, a kezdeti befektetés összegét levonják az összes jelenérték összegéből:

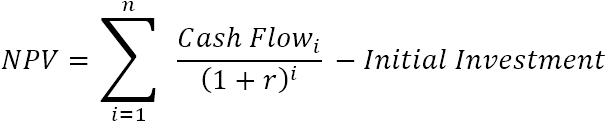
Hol:

• r - diszkont vagy kamatláb
• n - az időszakok száma
• i - a pénzforgalmi időszak

Mivel minden nullától eltérő, nullával hatványozott szám egyenlő 1-gyel, a kezdeti beruházást is beleszámíthatjuk az összegbe. Vegyük észre, hogy az NPV-képlet e kompakt változatában i=0, azaz a kezdeti beruházás a 0. időszakban történik.

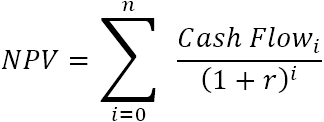
Például, ha egy 10%-kal diszkontált pénzáramlás-sorozat (50, 60, 70) és 100 dolláros kezdeti költség mellett szeretné megtalálni az NPV-t, akkor a következő képletet használhatja:

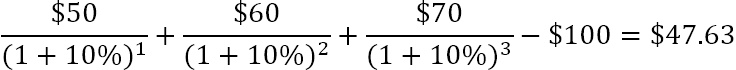
Vagy

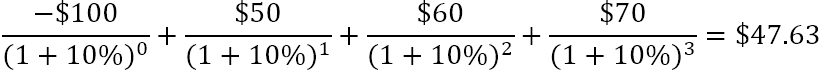
Hogyan segít a nettó jelenérték egy tervezett beruházás pénzügyi életképességének értékelésében? Feltételezzük, hogy egy pozitív NPV-vel rendelkező beruházás nyereséges, egy negatív NPV-vel rendelkező beruházás pedig veszteséges. Ez a koncepció az alapja a Nettó jelenérték szabály , amely szerint csak pozitív nettó jelenértékkel rendelkező projektekben szabad részt venni.

Excel NPV funkció

Az Excel NPV funkciója egy diszkont vagy kamatláb és egy sor jövőbeli pénzáramlás alapján adja meg egy befektetés nettó jelenértékét.

Az Excel NPV függvény szintaxisa a következő:

Hol:

• Rate (kötelező) - a diszkontráta vagy kamatláb egy időszakra vonatkozóan, amelyet százalékban vagy megfelelő tizedesjegyben kell megadni.
• Value1, [value2], ... - numerikus értékek, amelyek rendszeres pénzáramlások sorozatát képviselik. Érték1 kötelező, a további értékek opcionálisak. Az Excel 2007 és 2019 közötti modern verzióiban legfeljebb 254 értékargumentum adható meg; az Excel 2003 és régebbi verziókban legfeljebb 30 argumentum.

Az NPV funkció az Excel 365 - 2000 programban érhető el.

Tippek:

• A járadék jelenértékének kiszámításához használja az Excel PV funkcióját.
• A befektetés várható megtérülésének becsléséhez végezze el az IRR-számítást.

4 dolog, amit az NPV funkcióról tudni kell

Annak érdekében, hogy az Excelben az NPV-képletet helyesen számítsa ki, kérjük, tartsa szem előtt az alábbi tényeket:

• Az értékeknek a minden időszak végén Ha az első pénzáramlás (kezdeti befektetés) a az első időszak kezdete , használja az alábbi NPV-képletek egyikét.
• Az értékeket a időrendi sorrend és időben egyenlően elosztva .
• Használja a címet. negatív értékek a kiáramlások (kifizetett pénzeszközök) és pozitív értékek a beáramlásokat (kapott pénzeszközöket) képviselik.
• Csak számértékek Az üres cellákat, a számok szöveges megjelenítését, a logikai értékeket és a hibaértékeket figyelmen kívül hagyjuk.

Hogyan működik az Excel NPV funkció

Az NPV függvény használata az Excelben kissé trükkös a függvény megvalósításának módja miatt. Alapértelmezés szerint feltételezzük, hogy a beruházás egy periódussal a beruházás előtt egy periódussal történik. value1 Emiatt az NPV-képlet tiszta formában csak akkor működik megfelelően, ha a kezdeti beruházási költséget megadjuk. egy periódus mától számítva , ma nem!

Ennek illusztrálására számítsuk ki a nettó jelenértéket kézzel és egy Excel NPV képlettel, és hasonlítsuk össze az eredményeket.

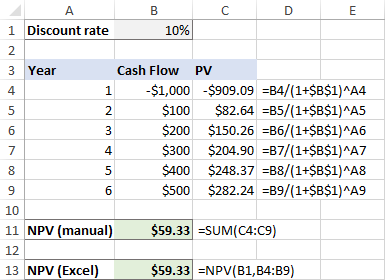
Tegyük fel, hogy B1-ben van egy diszkontráta, B4:B9-ben egy pénzáramlási sorozat, A4:A9-ben pedig időszakszámok.

Adja meg a fenti hivatkozásokat ebben az általános PV-képletben:

PV = jövőbeli érték/(1+kamatláb)^időszak

És a következő egyenletet kapjuk:

=B4/(1+$B$1)^A4

Ez a képlet a C4-be kerül, majd átmásolódik az alábbi cellákba. Az abszolút és relatív cellahivatkozások okos használatának köszönhetően a képlet tökéletesen igazodik minden sorhoz, ahogy az alábbi képernyőképen látható.

Kérjük, vegye figyelembe, hogy a kezdeti beruházás jelenértékét is kiszámítjuk, mivel a kezdeti beruházási költség 1 év után , így ez is kedvezményes.

Ezután összegezzük az összes jelenértéket:

=SUM(C4:C9)

Most pedig végezzük el az NPV-t az Excel függvény segítségével:

=NPV(B1, B4:B9)

Mint látható, mindkét számítás eredménye pontosan megegyezik:

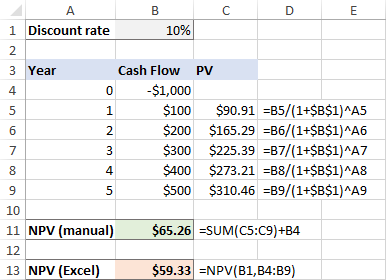
De mi van akkor, ha a kezdeti kiadás a az első időszak kezdete , ahogyan az jellemzően történik?

Mivel a kezdeti befektetés ma történik, nem kell diszkontálni, és ezt az összeget egyszerűen hozzáadjuk a jövőbeli pénzáramlások jelenértékének összegéhez (mivel ez egy negatív szám, valójában levonjuk):

=SUM(C4:C9)+B4

És ebben az esetben a kézi számítás és az Excel NPV funkciója eltérő eredményeket ad:

Ez azt jelenti, hogy nem támaszkodhatunk az Excelben található NPV képletre, és ebben a helyzetben kézzel kell kiszámítanunk a nettó jelenértéket? Természetesen nem! Csak egy kicsit meg kell csípnünk az NPV függvényt, ahogyan azt a következő részben elmagyarázzuk.

Hogyan számítsuk ki az NPV-t Excelben

Amikor a kezdeti beruházás a az első időszak kezdete , úgy kezelhetjük, mint az előző időszak végén (azaz a 0. időszakban) keletkezett pénzáramlást. Ezt szem előtt tartva két egyszerű módja van az NPV kiszámításának Excelben.

Excel NPV képlet 1

A kezdeti költséget hagyja ki az értéktartományból, és vonja ki az NPV függvény eredményéből. Mivel a kezdeti költséget jellemzően a negatív szám , ténylegesen elvégzi az összeadási műveletet:

Ebben az esetben az Excel NPV függvénye csak a páratlan pénzáramlások jelenértékét adja vissza. Mivel "nettó" értéket szeretnénk (azaz a jövőbeli pénzáramlások jelenértékét, csökkentve a kezdeti befektetéssel), az NPV függvényen kívül levonjuk a kezdeti költségeket.

Excel NPV képlet 2

Vegye be a kezdeti költséget az értéktartományba, és szorozza meg az eredményt (1 + ráta).

Ebben az esetben az Excel NPV függvénye a -1-es periódustól adná az eredményt (mintha a kezdeti beruházás egy periódussal a 0. periódus előtt történt volna), meg kell szoroznunk a kimenetét (1 + r) értékkel, hogy az NPV-t egy periódussal előrehozzuk (azaz i = -1-től i = 0-ig). Kérjük, tekintse meg az NPV-képlet kompakt formáját.

Az, hogy melyik képletet használod, személyes preferencia kérdése. Én személy szerint az elsőt tartom egyszerűbbnek és könnyebben érthetőnek.

NPV kalkulátor Excelben

Lássuk, hogyan használhatja a fenti képleteket valós adatokon, hogy saját NPV-kalkulátort készítsen az Excelben.

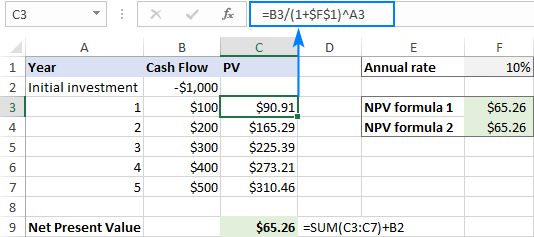
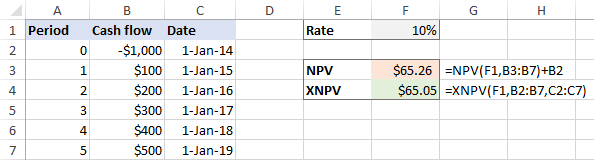
Tegyük fel, hogy a kezdeti kiadás B2-ben, a jövőbeli pénzáramlások sorozata B3:B7-ben és a szükséges megtérülési ráta F1-ben található. Az NPV kiszámításához használja az alábbi képletek egyikét:

NPV képlet 1:

=NPV(F1, B3:B7) + B2

Vegye észre, hogy az első értékargumentum az 1. időszak pénzforgalma (B3), a kezdeti költség (B2) nincs benne.

NPV képlet 2:

=NPV(F1, B2:B7) * (1+F1)

Ez a képlet tartalmazza a kezdeti költséget (B2) az értéktartományban.

Az alábbi képernyőkép az Excel NPV-kalkulátorunkat mutatja be működés közben:

Hogy megbizonyosodjunk arról, hogy az Excel NPV képleteink helyesek, ellenőrizzük az eredményt kézi számításokkal.

Először is, a fent tárgyalt PV képlet segítségével meghatározzuk az egyes pénzáramlások jelenértékét:

=B3/(1+$F$1)^A3

Ezután adjuk össze az összes jelenértéket, és vonjuk le a beruházás kezdeti költségét:

=SUM(C3:C7)+B2

... és láthatjuk, hogy mindhárom képlet eredménye teljesen megegyezik.

Megjegyzés: Ebben a példában éves cash flow-kkal és éves rátával foglalkozunk. Ha meg kell találni a negyedévente vagy havonta NPV-t az Excelben, győződjön meg róla, hogy a diszkontálási rátát ennek megfelelően módosította, ahogyan azt a példa elmagyarázza.

A PV és az NPV közötti különbség Excelben

A pénzügyekben mind a PV, mind az NPV a jövőbeli pénzáramlások jelenlegi értékének mérésére szolgál a jövőbeli összegek jelenre történő diszkontálásával. Egy fontos dologban azonban különböznek egymástól:

• Jelenérték (PV) - egy adott időszak összes jövőbeli pénzbevételére vonatkozik.
• Nettó jelenérték (NPV) - a pénzbevételek jelenértéke és a pénzkiáramlások jelenértéke közötti különbség.

Más szóval, a PV csak a pénzbeáramlásokat veszi figyelembe, míg az NPV a kezdeti beruházást vagy kiadást is figyelembe veszi, így nettó értéket kapunk.

A Microsoft Excelben két alapvető különbség van a funkciók között:

• Az NPV függvény képes kiszámítani az egyenlőtlen (változó) pénzáramlásokat. A PV függvény megköveteli, hogy a pénzáramlások a beruházás teljes élettartama alatt állandóak legyenek.
• Az NPV esetében a pénzáramlásoknak minden időszak végén kell bekövetkezniük. A PV képes kezelni az időszak végén és elején bekövetkező pénzáramlásokat.

Az NPV és az XNPV közötti különbség Excelben

Az XNPV egy újabb Excel pénzügyi funkció, amely kiszámítja egy befektetés nettó jelenértékét. Az elsődleges különbség a funkciók között a következő:

• Az NPV minden időszakot egyenlő .
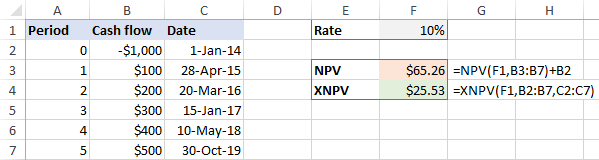
• Az XNPV lehetővé teszi az egyes cash flow-knak megfelelő dátumok megadását. Ezért az XNPV funkció sokkal pontosabb, ha cash flow-k sorozatával van dolgunk a következő időpontokban szabálytalan időközök .

Az NPV-vel ellentétben az Excel XNPV funkciója "normálisan" van végrehajtva - az első érték a beruházás kezdetén bekövetkező kiáramlásnak felel meg. Minden egymást követő pénzáramlást 365 napos év alapján diszkontálnak.

Az XNPV függvény szintaxisát tekintve egy további argumentummal rendelkezik:

Példaként használjuk mindkét függvényt ugyanazon az adatsoron, ahol F1 a diszkontráta, B2:B7 a pénzáramlások és C2:C7 a dátumok:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Ha a pénzáramlások elosztva egyenletesen a beruházáson keresztül az NPV és az XNPV függvények nagyon közeli értékeket adnak vissza:

Amennyiben a szabálytalan időközök , az eredmények közötti különbség nagyon jelentős:

Gyakori hibák az NPV kiszámításakor Excelben

Az NPV függvény meglehetősen sajátos megvalósítása miatt sok hibát követnek el a nettó jelenérték kiszámításakor az Excelben. Az alábbi egyszerű példák a legjellemzőbb hibákat és azok elkerülését mutatják be.

Szabálytalan időközök

Az Excel NPV funkciója feltételezi, hogy minden pénzforgalmi időszak egyenlő Ha különböző intervallumokat ad meg, mondjuk éveket és negyedéveket vagy hónapokat, a nettó jelenérték nem lesz helyes a nem koherens időszakok miatt.

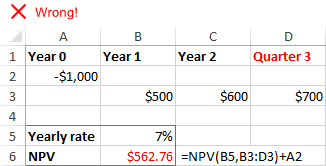
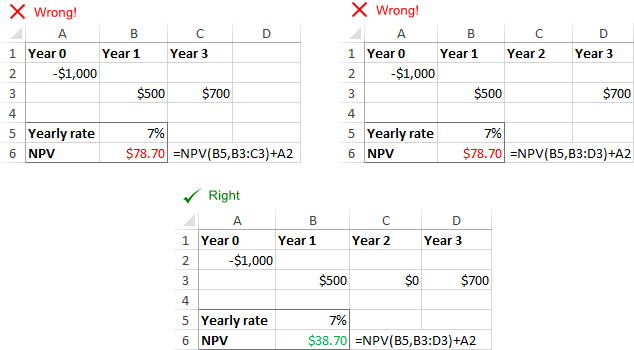
Hiányzó időszakok vagy pénzmozgások

Az Excelben az NPV nem ismeri fel a kihagyott időszakokat, és figyelmen kívül hagyja az üres cellákat. Az NPV helyes kiszámításához kérjük, adja meg a következőket egymás után hónapok, negyedévek vagy évek és a kínálat nulla értékek olyan időszakokra, amelyeknek nulla pénzáramlásuk van.

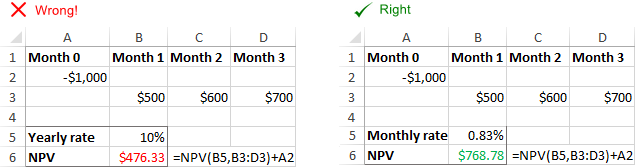
A diszkontálási ráta nem felel meg a tényleges időszakoknak

Az Excel NPV függvény nem tudja automatikusan a megadott időfrekvenciákhoz igazítani a szolgáltatott rátát, például az éves diszkontrátát a havi pénzáramlásokhoz. időszakonként megfelelő arány .

Helytelen sebesség formátum

A diszkont vagy kamatlábat a következő formában kell megadni százalékos arány vagy a megfelelő decimális szám Például a 10 százalékos kamatlábat megadhatja 10% vagy 0,1. Ha a kamatlábat 10-es számként adja meg, az Excel 1000%-nak fogja kezelni, és az NPV rosszul lesz kiszámítva.

Így használhatja az NPV-t Excelben egy befektetés nettó jelenértékének kiszámításához. Ha közelebbről meg szeretné nézni az ebben a bemutatóban tárgyalt képleteket, kérjük, töltse le az Excel NPV-kalkulátor mintáját.

Köszönjük, hogy elolvastátok, és reméljük, hogy jövő héten találkozunk a blogunkon!