இந்த டுடோரியலில், முதலீட்டின் நிகர தற்போதைய மதிப்பைக் கணக்கிட எக்செல் என்பிவி செயல்பாட்டை எவ்வாறு பயன்படுத்துவது மற்றும் எக்செல் இல் என்பிவி செய்யும் போது பொதுவான பிழைகளைத் தவிர்ப்பது எப்படி என்பதை நீங்கள் கற்றுக் கொள்வீர்கள்.

நிகர தற்போதைய மதிப்பு அல்லது நிகர தற்போதைய மதிப்பு என்பது ஒரு திட்டம் லாபகரமானதா இல்லையா என்பதைக் குறிக்கும் நிதிப் பகுப்பாய்வின் முக்கிய அங்கமாகும். நிகர தற்போதைய மதிப்பு ஏன் மிகவும் முக்கியமானது? ஏனென்றால், எதிர்காலத்தில் பெறக்கூடிய பணத்தின் மதிப்பு, தற்போது உங்களிடம் உள்ள அதே அளவு பணத்தை விடக் குறைவாக இருக்கும் என்று அடிப்படை நிதிக் கருத்து உள்ளது. நிகர தற்போதைய மதிப்பு அவர்களின் இன்றைய மதிப்பைக் காட்ட எதிர்காலத்தில் எதிர்பார்க்கப்படும் பணப்புழக்கங்களைத் தள்ளுபடி செய்கிறது.

மைக்ரோசாப்ட் எக்செல் NPVயைக் கணக்கிடுவதற்கு ஒரு சிறப்புச் செயல்பாட்டைக் கொண்டுள்ளது, ஆனால் குறிப்பாக சிறிய அனுபவம் உள்ளவர்களுக்கு இதன் பயன்பாடு தந்திரமானதாக இருக்கும். நிதி மாதிரியாக்கத்தில். இந்தக் கட்டுரையின் நோக்கம், எக்செல் NPV செயல்பாடு எவ்வாறு செயல்படுகிறது என்பதைக் காண்பிப்பது மற்றும் எக்செல் இல் தொடர்ச்சியான பணப்புழக்கங்களின் நிகர தற்போதைய மதிப்பைக் கணக்கிடும் போது சாத்தியமான ஆபத்துகளைச் சுட்டிக்காட்டுவது.

நிகரம் என்றால் என்ன தற்போதைய மதிப்பு (NPV)?

நிகர தற்போதைய மதிப்பு (NPV) என்பது தற்போது தள்ளுபடி செய்யப்பட்ட திட்டத்தின் முழு ஆயுளிலும் தொடர்ச்சியான பணப்புழக்கங்களின் மதிப்பாகும்.

எளிமையான வார்த்தைகளில், NPV ஆரம்ப முதலீட்டுச் செலவைக் காட்டிலும் குறைவான எதிர்கால பணப்புழக்கங்களின் தற்போதைய மதிப்பாக வரையறுக்கப்படலாம்:

NPV = எதிர்கால பணப்புழக்கங்களின் PV – ஆரம்ப முதலீடு

நன்றாக புரிந்து கொள்ளபூஜ்ய பணப்புழக்கங்களைக் கொண்ட காலங்கள்.

தள்ளுபடி விகிதம் உண்மையான காலகட்டங்களுடன் ஒத்துப்போவதில்லை

எக்செல் NPV செயல்பாட்டால் வழங்கப்பட்ட விகிதத்தை கொடுக்கப்பட்ட நேரத்திற்கு சரிசெய்ய முடியாது அதிர்வெண்கள் தானாகவே, எடுத்துக்காட்டாக, மாதாந்திர பணப்புழக்கங்களுக்கான வருடாந்திர தள்ளுபடி விகிதம். ஒரு காலத்திற்குப் பொருத்தமான விகிதத்தை வழங்குவது பயனரின் பொறுப்பாகும்.

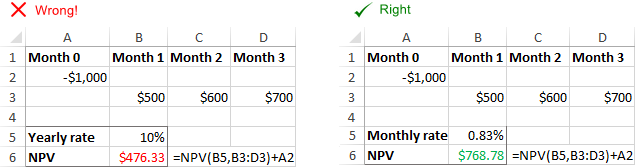
தவறான விகித வடிவம்

தள்ளுபடி அல்லது வட்டி விகிதம் இருக்க வேண்டும் சதவீதம் அல்லது தொடர்புடைய தசம எண்ணாக வழங்கப்படுகிறது. எடுத்துக்காட்டாக, 10 சதவீத விகிதம் 10% அல்லது 0.1 என வழங்கப்படலாம். நீங்கள் விகிதத்தை எண் 10 ஆக உள்ளிட்டால், எக்செல் அதை 1000% எனக் கருதும், மேலும் NPV தவறாகக் கணக்கிடப்படும்.

எக்செல் இல் NPVஐப் பயன்படுத்தி நிகரத்தைக் கண்டறியலாம். முதலீட்டின் தற்போதைய மதிப்பு. இந்த டுடோரியலில் விவாதிக்கப்பட்ட சூத்திரங்களை உன்னிப்பாகப் பார்க்க, Excel க்கான எங்கள் மாதிரி NPV கால்குலேட்டரைப் பதிவிறக்க தயங்க வேண்டாம்.

படித்ததற்கு நன்றி, அடுத்த வாரம் எங்கள் வலைப்பதிவில் உங்களைப் பார்ப்போம் என்று நம்புகிறேன்!

ஒரு ஒற்றை பணப்புழக்கத்திற்கு, தற்போதைய மதிப்பு (PV) இந்த சூத்திரத்தில் கணக்கிடப்படுகிறது:

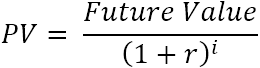
எங்கே :

• r – தள்ளுபடி அல்லது வட்டி விகிதம்
• i – பணப்புழக்கம் காலம்

உதாரணமாக, 1 வருடத்திற்கு பிறகு $110 (எதிர்கால மதிப்பு) பெற (i), 10% வருடாந்திர வட்டி விகிதம் (r) வழங்கும் உங்கள் வங்கிக் கணக்கில் இன்று எவ்வளவு முதலீடு செய்ய வேண்டும்? மேலே உள்ள சூத்திரம் இந்த பதிலை அளிக்கிறது:

$110/(1+10%)^1 = $100

வேறுவிதமாகக் கூறினால், $100 என்பது எதிர்காலத்தில் பெறப்படும் என எதிர்பார்க்கப்படும் $110 இன் தற்போதைய மதிப்பு.

நிகர தற்போதைய மதிப்பு. (NPV) அனைத்து எதிர்கால பணப்புழக்கங்களின் தற்போதைய மதிப்புகளை நிகழ்காலத்தில் ஒரு புள்ளிக்குக் கொண்டுவருகிறது. மேலும், "நிகர" யோசனையானது, திட்டத்திற்கு நிதியளிக்கத் தேவையான ஆரம்ப மூலதன முதலீட்டைக் கணக்கிட்ட பிறகு, அது எவ்வளவு லாபகரமானதாக இருக்கும் என்பதைக் காட்டுவதாகும் என்பதால், ஆரம்ப முதலீட்டின் அளவு, தற்போதுள்ள அனைத்து மதிப்புகளின் கூட்டுத்தொகையிலிருந்து கழிக்கப்படுகிறது:

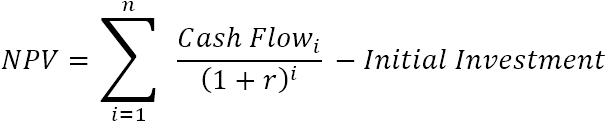
எங்கே:

• r – தள்ளுபடி அல்லது வட்டி வீதம்
• n – கால இடைவெளிகளின் எண்ணிக்கை
• i – the பணப்புழக்க காலம்

பூஜ்ஜிய சக்திக்கு உயர்த்தப்படும் பூஜ்ஜியம் அல்லாத எண் 1 க்கு சமமாக இருப்பதால், ஆரம்ப முதலீட்டை நாம் தொகையில் சேர்க்கலாம். தயவு செய்து கவனிக்கவும், NPV சூத்திரத்தின் இந்த சிறிய பதிப்பில், i=0, அதாவது ஆரம்ப முதலீடு 0 கால கட்டத்தில் செய்யப்படுகிறது பணப்புழக்கங்களின் தொடர் (50, 60, 70) 10% தள்ளுபடி மற்றும் ஆரம்ப செலவு$100, நீங்கள் இந்த சூத்திரத்தைப் பயன்படுத்தலாம்:

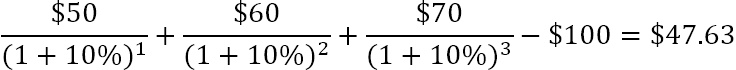
அல்லது

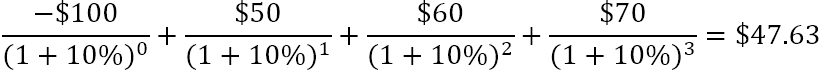
நிகர தற்போதைய மதிப்பு நிதியை மதிப்பிடுவதில் எவ்வாறு உதவுகிறது முன்மொழியப்பட்ட முதலீட்டின் நம்பகத்தன்மை? நேர்மறை NPV கொண்ட முதலீடு லாபகரமாக இருக்கும் என்றும், எதிர்மறை NPV உள்ள முதலீடு லாபமற்றதாக இருக்கும் என்றும் கருதப்படுகிறது. இந்த கருத்து நிகர தற்போதைய மதிப்பு விதி ன் அடிப்படையாகும், இது நேர்மறையான நிகர தற்போதைய மதிப்பைக் கொண்ட திட்டங்களில் மட்டுமே நீங்கள் ஈடுபட வேண்டும் என்று கூறுகிறது.

Excel NPV செயல்பாடு

தி Excel இல் NPV செயல்பாடு தள்ளுபடி அல்லது வட்டி விகிதம் மற்றும் எதிர்கால பணப்புழக்கங்களின் தொடர் அடிப்படையில் முதலீட்டின் நிகர தற்போதைய மதிப்பை வழங்குகிறது.

எக்செல் NPV செயல்பாட்டின் தொடரியல் பின்வருமாறு:

எங்கே:

• வீதம் (தேவை) - ஒரு காலத்தில் தள்ளுபடி அல்லது வட்டி விகிதம். இது சதவீதம் அல்லது தொடர்புடைய தசம எண்ணாக வழங்கப்பட வேண்டும்.
• மதிப்பு1, [மதிப்பு2], … - வழக்கமான பணப்புழக்கங்களின் வரிசையைக் குறிக்கும் எண் மதிப்புகள். மதிப்பு1 தேவை, அடுத்தடுத்த மதிப்புகள் விருப்பமானவை. எக்செல் 2007 முதல் 2019 வரையிலான நவீன பதிப்புகளில், 254 மதிப்பு வாதங்கள் வரை வழங்கப்படலாம்; எக்செல் 2003 மற்றும் அதற்குப் பழைய - 30 வாதங்கள் வரை வருடாந்திரத்தின் தற்போதைய மதிப்பு, Excel PV செயல்பாட்டைப் பயன்படுத்தவும்.
• முதலீட்டின் மீதான திட்டமிடப்பட்ட வருவாயைக் கணக்கிட, IRR கணக்கீட்டைச் செய்யவும்.

4 விஷயங்களைச் செய்யுங்கள்.NPV செயல்பாட்டைப் பற்றி தெரிந்து கொள்ள வேண்டும்

எக்செல் இல் உள்ள உங்கள் NPV சூத்திரம் சரியாக கணக்கிடப்படுவதை உறுதிசெய்ய, இந்த உண்மைகளை நினைவில் கொள்ளவும்:

• ஒவ்வொரு காலகட்டத்தின் இறுதியிலும் மதிப்புகள் நிகழ வேண்டும். . முதல் பணப்புழக்கம் (ஆரம்ப முதலீடு) முதல் காலகட்டத்தின் தொடக்கத்தில் ஏற்பட்டால், இந்த NPV சூத்திரங்களில் ஒன்றைப் பயன்படுத்தவும்.
• மதிப்புகள் காலவரிசைப்படி வழங்கப்பட வேண்டும். மற்றும் சமமான இடைவெளியில் .
• வெளியேற்றங்களைக் குறிக்க எதிர்மறை மதிப்புகளைப் பயன்படுத்தவும் (பணம் செலுத்தப்பட்டது) மற்றும் நேர்மறை மதிப்புகளைப் பிரதிநிதித்துவப்படுத்த (பணம் பெறப்பட்டது) ).
• எண் மதிப்புகள் மட்டுமே செயலாக்கப்படும். வெற்று செல்கள், எண்களின் உரைப் பிரதிநிதித்துவங்கள், தருக்க மதிப்புகள் மற்றும் பிழை மதிப்புகள் புறக்கணிக்கப்படுகின்றன.

எக்செல் NPV செயல்பாடு எவ்வாறு செயல்படுகிறது

எக்செல் இல் NPV செயல்பாட்டைப் பயன்படுத்துவது சற்று தந்திரமானது. செயல்பாடு செயல்படுத்தப்படும் விதம். முன்னிருப்பாக, மதிப்பு1 தேதிக்கு ஒரு காலகட்டத்திற்கு முன் முதலீடு செய்யப்பட்டதாகக் கருதப்படுகிறது. இந்தக் காரணத்திற்காக, NPV ஃபார்முலா அதன் தூய வடிவத்தில், ஆரம்ப முதலீட்டுச் செலவை இப்போதிலிருந்து வழங்கினால் மட்டுமே சரியாகச் செயல்படும், இன்று அல்ல!

இதை விளக்குவதற்கு, நிகர தற்போதைய மதிப்பைக் கணக்கிடுவோம். கைமுறையாக மற்றும் எக்செல் NPV சூத்திரத்துடன், முடிவுகளை ஒப்பிட்டுப் பாருங்கள்.

உங்களிடம் B1 இல் தள்ளுபடி விகிதம் உள்ளது, B4:B9 இல் தொடர்ச்சியான பணப்புழக்கங்கள் மற்றும் A4:A9 இல் கால எண்கள் உள்ளன என்று வைத்துக்கொள்வோம்.

இந்த பொதுவான PV சூத்திரத்தில் மேலே உள்ள குறிப்புகளை வழங்கவும்:

PV = எதிர்காலம்மதிப்பு/(1+ரேட்)^காலம்

மேலும் நீங்கள் பின்வரும் சமன்பாட்டைப் பெறுவீர்கள்:

=B4/(1+$B$1)^A4

இந்த சூத்திரம் C4 க்கு சென்று பின்னர் கீழே உள்ள கலங்களுக்கு நகலெடுக்கப்படும். முழுமையான மற்றும் தொடர்புடைய செல் குறிப்புகளின் புத்திசாலித்தனமான பயன்பாட்டின் காரணமாக, கீழே உள்ள ஸ்கிரீன்ஷாட்டில் காட்டப்பட்டுள்ளபடி ஒவ்வொரு வரிசையிலும் சூத்திரம் சரியாகச் சரிசெய்கிறது.

ஆரம்ப முதலீட்டுச் செலவில் இருந்து ஆரம்ப முதலீட்டின் தற்போதைய மதிப்பையும் கணக்கிடுகிறோம் என்பதைக் கவனியுங்கள். 1 வருடத்திற்குப் பிறகு , அதனால் அதுவும் தள்ளுபடி செய்யப்படுகிறது.

அதன் பிறகு, தற்போதைய மதிப்புகள் அனைத்தையும் தொகுக்கிறோம்:

=SUM(C4:C9)

இப்போது, ​​நாம் எக்செல் செயல்பாட்டுடன் NPV செய்யுங்கள்:

=NPV(B1, B4:B9)

நீங்கள் பார்க்கிறபடி, இரண்டு கணக்கீடுகளின் முடிவுகளும் சரியாகப் பொருந்துகின்றன:

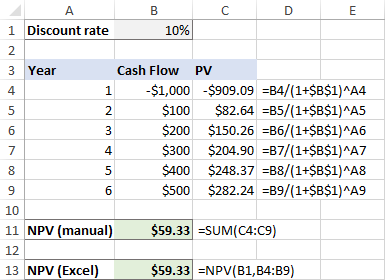
ஆனால் என்ன ஆரம்பச் செலவு முதல் காலகட்டத்தின் தொடக்கத்தில் ஏற்பட்டால், அது வழக்கமாகச் செய்வது போல்?

இன்று ஆரம்ப முதலீடு செய்யப்படுவதால், அதற்கு எந்தத் தள்ளுபடியும் பொருந்தாது, மேலும் இந்தத் தொகையைச் சேர்ப்போம். எதிர்கால பணப்புழக்கங்களின் தற்போதைய மதிப்புகளின் கூட்டுத்தொகைக்கு (இது எதிர்மறை எண் என்பதால், அது உண்மையில் கழிக்கப்படுகிறது):

=SUM(C4:C9)+B4

மேலும் இந்த விஷயத்தில், கைமுறை கணக்கீடு மற்றும் எக்செல் NPV செயல்பாடு விளைச்சல் வெவ்வேறு முடிவுகள்:

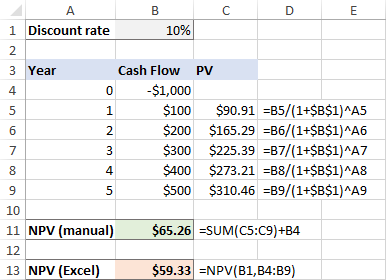
இதற்கு நாம் NPVயை நம்பியிருக்க முடியாது என்று அர்த்தமா எக்செல் இல் முலா மற்றும் இந்த சூழ்நிலையில் நிகர தற்போதைய மதிப்பை கைமுறையாக கணக்கிட வேண்டுமா? நிச்சயமாக இல்லை! அடுத்த பகுதியில் விளக்கப்பட்டுள்ளபடி நீங்கள் NPV செயல்பாட்டை சிறிது மாற்றியமைக்க வேண்டும்.

எக்செல் இல் NPV ஐ எவ்வாறு கணக்கிடுவது

ஆரம்ப முதலீடு போது முதல் காலகட்டத்தின் தொடக்கத்தில் ஆனது, முந்தைய காலகட்டத்தின் முடிவில் (அதாவது காலம் 0) பணப்புழக்கமாக இதை நாம் கருதலாம். அதைக் கருத்தில் கொண்டு, எக்செல் இல் NPVயைக் கண்டறிய இரண்டு எளிய வழிகள் உள்ளன.

எக்செல் NPV சூத்திரம் 1

ஆரம்பச் செலவை மதிப்புகளின் வரம்பிலிருந்து விட்டுவிட்டு NPV செயல்பாட்டின் முடிவிலிருந்து கழிக்கவும். . ஆரம்ப செலவு பொதுவாக எதிர்மறை எண்ணாக உள்ளிடப்பட்டதால், நீங்கள் உண்மையில் கூட்டல் செயல்பாட்டைச் செய்கிறீர்கள்:

இந்த நிலையில், எக்செல் NPV செயல்பாடு திரும்பும் சீரற்ற பணப்புழக்கங்களின் தற்போதைய மதிப்பு. "நிகரம்" (அதாவது எதிர்கால பணப்புழக்கத்தின் தற்போதைய மதிப்பு குறைவான ஆரம்ப முதலீடு) என்பதால், NPV செயல்பாட்டிற்கு வெளியே ஆரம்ப செலவைக் கழிப்போம்.

Excel NPV ஃபார்முலா 2

ஆரம்பச் செலவைச் சேர்க்கவும். மதிப்புகளின் வரம்பில் மற்றும் முடிவை (1 + விகிதம்) ஆல் பெருக்கவும்.

இந்த வழக்கில், Excel NPV செயல்பாடு உங்களுக்கு காலம் -1 இன் முடிவை வழங்கும் (ஆரம்ப முதலீடு ஒரு காலகட்டமாக செய்யப்பட்டது போல் காலம் 0 க்கு முன்), NPV ஐ ஒரு காலத்தில் முன்னோக்கி கொண்டு வர அதன் வெளியீட்டை (1 + r) ஆல் பெருக்க வேண்டும் (அதாவது i = -1 இலிருந்து i = 0 வரை). NPV சூத்திரத்தின் சுருக்கமான படிவத்தைப் பார்க்கவும்.

எந்த சூத்திரத்தைப் பயன்படுத்துவது என்பது உங்கள் தனிப்பட்ட விருப்பம். முதலாவது எளிமையானது மற்றும் புரிந்துகொள்ள எளிதானது என்று நான் தனிப்பட்ட முறையில் நம்புகிறேன்.

எக்செல் இல் NPV கால்குலேட்டர்

இப்போது மேலே உள்ளவற்றை நீங்கள் எவ்வாறு பயன்படுத்தலாம் என்பதைப் பார்ப்போம்எக்செல் இல் உங்களின் சொந்த NPV கால்குலேட்டரை உருவாக்குவதற்கான உண்மையான தரவுகளின் சூத்திரங்கள் NPVஐக் கண்டறிய, பின்வரும் சூத்திரங்களில் ஒன்றைப் பயன்படுத்தவும்:

NPV சூத்திரம் 1:

=NPV(F1, B3:B7) + B2

முதல் மதிப்பு மதிப்பு ரொக்கம் என்பதைக் கவனியுங்கள் காலம் 1 (B3) இல் ஓட்டம், ஆரம்ப செலவு (B2) சேர்க்கப்படவில்லை.

NPV ஃபார்முலா 2:

=NPV(F1, B2:B7) * (1+F1)

இந்த சூத்திரம் அடங்கும் மதிப்புகளின் வரம்பில் ஆரம்ப விலை (B2) சூத்திரங்கள் சரியானவை, கைமுறை கணக்கீடுகள் மூலம் முடிவைச் சரிபார்ப்போம்.

முதலில், மேலே விவாதிக்கப்பட்ட PV சூத்திரத்தைப் பயன்படுத்தி ஒவ்வொரு பணப்புழக்கத்தின் தற்போதைய மதிப்பைக் கண்டறியலாம்:

=B3/(1+$F$1)^A3

அடுத்து, தற்போதுள்ள எல்லா மதிப்புகளையும் கூட்டி, முதலீட்டின் ஆரம்பச் செலவைக் கழிக்கவும்:

=SUM(C3:C7)+B2

... மேலும் மூன்று சூத்திரங்களின் முடிவுகளும் முற்றிலும் ஒரே மாதிரியாக இருப்பதைப் பார்க்கவும்.

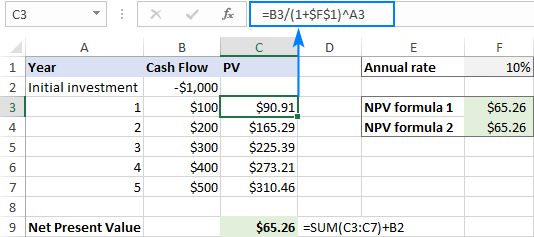
குறிப்பு. இந்த எடுத்துக்காட்டில், நாங்கள் வருடாந்திர பணப்புழக்கங்கள் மற்றும் வருடாந்திர வீதம் ஆகியவற்றைக் கையாளுகிறோம். நீங்கள் எக்செல் இல் காலாண்டு அல்லது மாதாந்திர NPV ஐக் கண்டுபிடிக்க விரும்பினால், இந்த எடுத்துக்காட்டில் விளக்கப்பட்டுள்ளபடி தள்ளுபடி விகிதத்தை அதற்கேற்ப சரிசெய்யவும்.

PV மற்றும் NPV இடையே உள்ள வேறுபாடு எக்செல்

நிதியில், PV மற்றும் NPV இரண்டும் எதிர்கால பணப்புழக்கங்களின் தற்போதைய மதிப்பை அளக்கப் பயன்படுகிறது. ஆனால்அவை ஒரு முக்கியமான வழியில் வேறுபடுகின்றன:

• தற்போதைய மதிப்பு (PV) - ஒரு குறிப்பிட்ட காலத்தில் அனைத்து எதிர்கால பண வரவுகளையும் குறிக்கிறது.
• நிகர நிகழ்காலம் மதிப்பு (NPV) - பண வரவுகளின் தற்போதைய மதிப்புக்கும் பண வரவுகளின் தற்போதைய மதிப்புக்கும் இடையே உள்ள வித்தியாசம்.

வேறுவிதமாகக் கூறினால், PV மட்டுமே பண வரவுகளைக் கணக்கிடுகிறது, NPVயும் கணக்கு ஆரம்ப முதலீடு அல்லது செலவினத்திற்கு, அதை நிகர எண்ணிக்கையாக மாற்றுகிறது.

மைக்ரோசாஃப்ட் எக்செல், செயல்பாடுகளுக்கு இடையே இரண்டு அத்தியாவசிய வேறுபாடுகள் உள்ளன:

• NPV செயல்பாடு சீரற்ற (மாறி) கணக்கிட முடியும் பணப்புழக்கங்கள். PV செயல்பாட்டிற்கு முதலீட்டின் முழு வாழ்க்கையிலும் பணப்புழக்கம் நிலையானதாக இருக்க வேண்டும்.
• NPV உடன், ஒவ்வொரு காலகட்டத்தின் முடிவிலும் பணப்புழக்கங்கள் ஏற்பட வேண்டும். ஒரு காலகட்டத்தின் இறுதியிலும் தொடக்கத்திலும் நிகழும் பணப்புழக்கங்களை PV கையாள முடியும்.

எக்செல் இல் NPV மற்றும் XNPV இடையே உள்ள வேறுபாடு

XNPV என்பது மேலும் ஒரு எக்செல் நிதிச் செயல்பாடு ஆகும். முதலீட்டின் தற்போதைய நிகர மதிப்பு. செயல்பாடுகளுக்கு இடையே உள்ள முதன்மை வேறுபாடு பின்வருமாறு:

• NPV எல்லா நேர காலங்களையும் சமம் என்று கருதுகிறது.
• XNPV ஒவ்வொரு தேதிக்கும் பொருந்தக்கூடிய தேதிகளைக் குறிப்பிட உங்களை அனுமதிக்கிறது பணப்புழக்கம். இந்த காரணத்திற்காக, XNPV செயல்பாடு ஒழுங்கற்ற இடைவெளியில் தொடர் பணப்புழக்கங்களைக் கையாளும் போது மிகவும் துல்லியமானது.

NPV போலல்லாமல், Excel XNPV செயல்பாடு "பொதுவாக செயல்படுத்தப்படுகிறது. " - முதல் மதிப்பு மணிக்கு நிகழும் வெளியேற்றத்திற்கு ஒத்திருக்கிறதுமுதலீட்டின் ஆரம்பம். அனைத்து தொடர்ச்சியான பணப்புழக்கங்களும் 365-நாள் வருடத்தின் அடிப்படையில் தள்ளுபடி செய்யப்படுகின்றன.

தொடரியல் அடிப்படையில், XNPV செயல்பாட்டிற்கு ஒரு கூடுதல் வாதம் உள்ளது:

உதாரணமாக , இரண்டு செயல்பாடுகளையும் ஒரே தரவுத் தொகுப்பில் பயன்படுத்துவோம், இதில் F1 என்பது தள்ளுபடி விகிதம், B2:B7 என்பது பணப்புழக்கங்கள் மற்றும் C2:C7 என்பது தேதிகள்:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

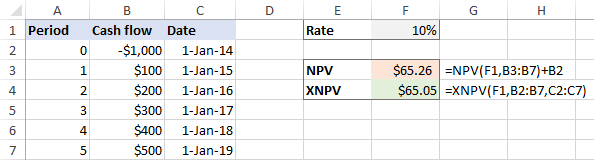
இல் ஒழுங்கற்ற இடைவெளிகள் , முடிவுகளுக்கிடையேயான வேறுபாடு மிகவும் குறிப்பிடத்தக்கது:

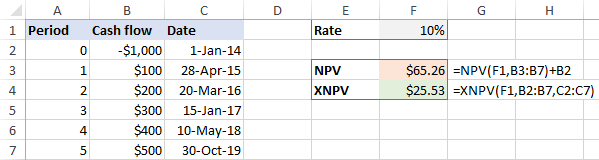
எக்செல் இல் NPV கணக்கிடும்போது ஏற்படும் பொதுவான பிழைகள்

காரணமாக NPV செயல்பாட்டின் மிகவும் குறிப்பிட்ட செயலாக்கம், எக்செல் இல் நிகர தற்போதைய மதிப்பைக் கணக்கிடும் போது பல பிழைகள் செய்யப்படுகின்றன. கீழே உள்ள எளிய எடுத்துக்காட்டுகள் மிகவும் பொதுவான பிழைகள் மற்றும் அவற்றை எவ்வாறு தவிர்ப்பது என்பதை நிரூபிக்கின்றன.

ஒழுங்கற்ற இடைவெளிகள்

எக்செல் NPV செயல்பாடு அனைத்து பணப்புழக்க காலங்களும் சமமாக இருக்கும் என்று கருதுகிறது. நீங்கள் வெவ்வேறு இடைவெளிகளை வழங்கினால், ஆண்டுகள் மற்றும் காலாண்டுகள் அல்லது மாதங்கள் எனக் கூறினால், ஒத்திசைவற்ற நேரக் காலங்கள் காரணமாக நிகர தற்போதைய மதிப்பு தவறாக இருக்கும்.

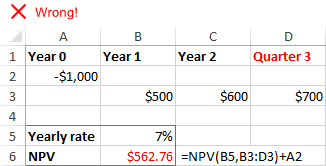
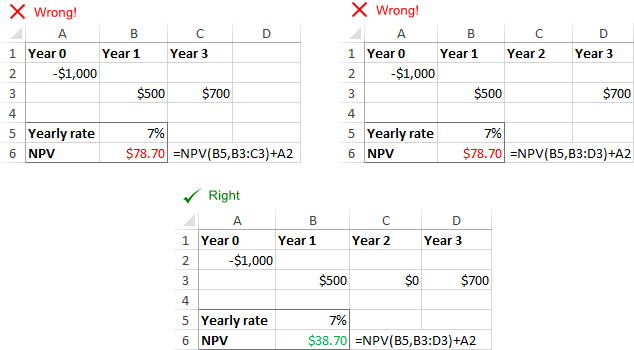
காணாமல் போன காலங்கள் அல்லது பணப்புழக்கங்கள்

எக்செல் இல் உள்ள NPV தவிர்க்கப்பட்ட காலங்களை அங்கீகரிக்காது மற்றும் வெற்று செல்களை புறக்கணிக்கிறது. NPV ஐ சரியாகக் கணக்கிட, தொடர்ந்து மாதங்கள், காலாண்டுகள் அல்லது வருடங்களை வழங்குவதை உறுதிசெய்து, பூஜ்ஜிய மதிப்புகளை குறிப்பிட்ட காலத்திற்கு வழங்கவும்