Šioje pamokoje sužinosite, kaip naudoti "Excel" funkciją NPV investicijų grynajai dabartinei vertei apskaičiuoti ir kaip išvengti dažniausiai pasitaikančių klaidų atliekant NPV "Excel" programoje.

Grynoji dabartinė vertė arba grynoji dabartinė vertė yra pagrindinis finansinės analizės elementas, kuris parodo, ar projektas bus pelningas, ar ne. Kodėl grynoji dabartinė vertė yra tokia svarbi? Todėl, kad pagrindinė finansų koncepcija teigia, jog pinigai, kurie potencialiai gali būti gauti ateityje, yra verti mažiau nei ta pati pinigų suma, kurią turite dabar. Grynoji dabartinė vertė diskontuoja pinigų srautus, kurių tikimasi ateityje, atgal į dabartį.parodyti savo šiandieninę vertę.

"Microsoft Excel" turi specialią funkciją grynajai dabartinei vertei apskaičiuoti, tačiau jos naudojimas gali būti sudėtingas, ypač žmonėms, kurie turi mažai patirties finansinio modeliavimo srityje. Šio straipsnio tikslas - parodyti, kaip veikia "Excel" NPV funkcija, ir atkreipti dėmesį į galimus keblumus apskaičiuojant grynąją dabartinę pinigų srautų serijos vertę "Excel" programoje.

Kas yra grynoji dabartinė vertė (NPV)?

Grynoji dabartinė vertė (NPV) - tai diskontuotų pinigų srautų per visą projekto įgyvendinimo laikotarpį vertė.

Paprastai NPV galima apibrėžti kaip būsimųjų pinigų srautų dabartinę vertę, atėmus pradines investicijų sąnaudas:

NPV = būsimųjų pinigų srautų PV - pradinė investicija

Kad geriau suprastumėte šią idėją, įsigilinkime į matematiką.

Vieno pinigų srauto dabartinė vertė (PV) apskaičiuojama pagal šią formulę:

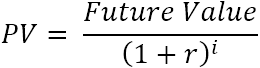
Kur:

• r - diskonto arba palūkanų norma
• i - pinigų srauto laikotarpis

Pavyzdžiui, norėdami po metų gauti 110 USD (būsimą vertę) (i), kiek šiandien turėtumėte investuoti į savo banko sąskaitą, kurioje siūloma 10 % metinė palūkanų norma (r)? Pagal pirmiau pateiktą formulę gausite šį atsakymą:

$110/(1+10%)^1 = $100

Kitaip tariant, 100 JAV dolerių yra dabartinė 110 JAV dolerių, kuriuos tikimasi gauti ateityje, vertė.

Grynoji dabartinė vertė (NPV) sudeda visų būsimųjų pinigų srautų dabartines vertes, kad jos pasiektų vieną dabarties tašką. Kadangi grynosios vertės idėja yra parodyti, koks bus projekto pelningumas, atsižvelgus į jam finansuoti reikalingas pradines kapitalo investicijas, iš visų dabartinių verčių sumos atimama pradinių investicijų suma:

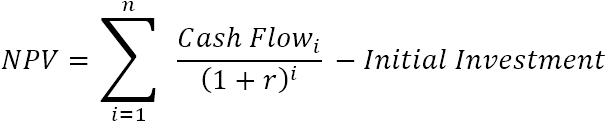
Kur:

• r - diskonto arba palūkanų norma
• n - laikotarpių skaičius
• i - pinigų srauto laikotarpis

Kadangi bet kuris nenulinis skaičius, pakeltas iki nulio laipsnio, yra lygus 1, į sumą galime įtraukti pradinę investiciją. Atkreipkite dėmesį, kad šioje sutrumpintoje NPV formulės versijoje i=0, t. y. pradinė investicija atliekama 0 laikotarpiu.

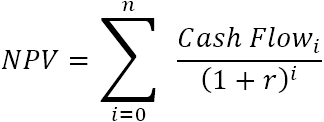
Pavyzdžiui, norėdami nustatyti grynąją dabartinę vertę pinigų srautų serijai (50, 60, 70), diskontuotai 10 % ir pradinėms 100 USD sąnaudoms, galite naudoti šią formulę:

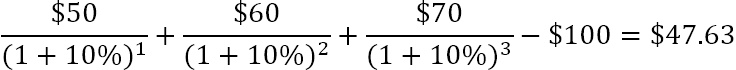
Arba

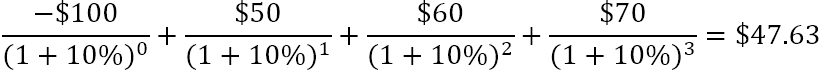
Kaip grynoji dabartinė vertė padeda įvertinti siūlomos investicijos finansinį gyvybingumą? Daroma prielaida, kad investicija, kurios grynoji dabartinė vertė yra teigiama, bus pelninga, o investicija, kurios grynoji dabartinė vertė yra neigiama, bus nuostolinga. Grynosios dabartinės vertės taisyklė , kuriame teigiama, kad turėtumėte dalyvauti tik tuose projektuose, kurių grynoji dabartinė vertė yra teigiama.

"Excel" NPV funkcija

"Excel" funkcija NPV pateikia grynąją dabartinę investicijos vertę, pagrįstą diskonto arba palūkanų norma ir būsimųjų pinigų srautų serija.

"Excel" NPV funkcijos sintaksė yra tokia:

Kur:

• Įvertinkite (privaloma) - diskonto arba palūkanų norma per vieną laikotarpį. Ji turi būti pateikta procentais arba atitinkamu dešimtainiu skaičiumi.
• Vertė1, [vertė2], ... - skaitmeninės vertės, rodančios eilę reguliarių pinigų srautų. Vertė1 privaloma, vėlesnės reikšmės yra neprivalomos. Šiuolaikinėse Excel 2007-2019 versijose galima pateikti iki 254 reikšmių argumentų, o Excel 2003 ir senesnėse - iki 30 argumentų.

NPV funkciją galima naudoti programoje "Excel 365-2000".

Patarimai:

• Norint apskaičiuoti dabartinę anuiteto vertę, naudokite "Excel" PV funkciją.
• Norėdami apskaičiuoti numatomą investicijų grąžą, atlikite IRR skaičiavimą.

4 dalykai, kuriuos turėtumėte žinoti apie NPV funkciją

Kad NPV formulė "Excel" programoje būtų apskaičiuota teisingai, nepamirškite šių faktų:

• Vertės turi atsirasti kiekvieno laikotarpio pabaigoje Jei pirmas pinigų srautas (pradinė investicija) atsiranda pirmojo laikotarpio pradžia , naudokite vieną iš šių NPV formulių.
• Reikšmės turi būti pateiktos chronologine tvarka ir vienodais laiko tarpais. .
• Naudokite neigiamas reikšmės, atspindinčios išleidžiamus (išmokėtus) ir teigiamas vertės, atspindinčios įplaukas (gautus pinigus).
• Tik skaitinės vertės Į tuščius langelius, tekstinius skaičių atvaizdus, logines reikšmes ir klaidų reikšmes neatsižvelgiama.

Kaip veikia "Excel" NPV funkcija

Naudoti NPV funkciją "Excel" programoje yra šiek tiek sudėtinga dėl to, kaip ši funkcija įgyvendinta. Pagal nutylėjimą daroma prielaida, kad investicija atliekama vienu laikotarpiu prieš vertė1 Dėl šios priežasties grynoji NPV formulė veikia teisingai tik tuo atveju, jei nurodomos pradinės investicijų sąnaudos. po vieno laikotarpio nuo dabar , bet ne šiandien!

Norėdami tai iliustruoti, apskaičiuokime grynąją dabartinę vertę rankiniu būdu ir naudodami "Excel" grynosios dabartinės vertės formulę ir palyginkime rezultatus.

Tarkime, turite diskonto normą B1, pinigų srautų eilutę B4:B9 ir laikotarpio numerius A4:A9.

Pateikite pirmiau nurodytas nuorodas šioje bendroje PV formulėje:

PV = būsimoji vertė/(1+procentas)^laikotarpis

Gausite šią lygtį:

=B4/(1+$B$1)^A4

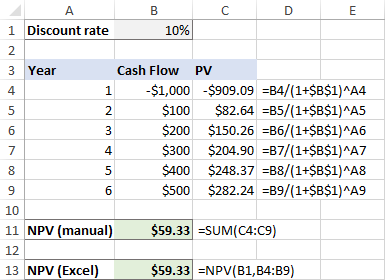
Ši formulė perkeliama į C4 ir nukopijuojama į toliau esančias ląsteles. Dėl sumaniai naudojamų absoliučiųjų ir santykinių ląstelių nuorodų formulė puikiai pritaikoma kiekvienai eilutei, kaip parodyta toliau pateiktoje ekrano nuotraukoje.

Atkreipkite dėmesį, kad apskaičiuojame ir dabartinę pradinės investicijos vertę, nes pradinės investicijos sąnaudos yra po 1 metų , todėl jam taip pat taikoma nuolaida.

Po to sudedame visas dabartines vertes:

=SUMA(C4:C9)

O dabar atlikime NPV su "Excel" funkcija:

=NPV(B1, B4:B9)

Kaip matote, abiejų skaičiavimų rezultatai tiksliai sutampa:

Tačiau ką daryti, jei pradinės išlaidos atsiranda pirmojo laikotarpio pradžia , kaip įprasta?

Kadangi pradinė investicija atliekama šiandien, jai netaikomas joks diskontavimas, todėl šią sumą tiesiog pridedame prie būsimųjų pinigų srautų dabartinių verčių sumos (kadangi tai neigiamas skaičius, jis iš tikrųjų atimamas):

=SUMA(C4:C9)+B4

Šiuo atveju rankiniu būdu atliktas skaičiavimas ir "Excel" NPV funkcija duoda skirtingus rezultatus:

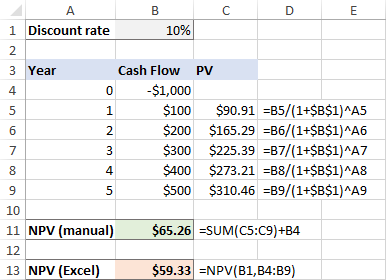
Ar tai reiškia, kad šioje situacijoje negalime pasikliauti "Excel" programa esančia NPV formule ir grynąją dabartinę vertę turime apskaičiuoti rankiniu būdu? Žinoma, ne! Jums tiesiog reikės šiek tiek patobulinti NPV funkciją, kaip paaiškinta kitame skyriuje.

Kaip apskaičiuoti grynąją dabartinę vertę "Excel" programoje

Kai pradinė investicija atliekama pirmojo laikotarpio pradžia , galime jį traktuoti kaip pinigų srautą praėjusio laikotarpio pabaigoje (t. y. 0 laikotarpiu). Atsižvelgdami į tai, yra du paprasti būdai, kaip "Excel" programoje rasti grynąją dabartinę vertę.

"Excel" NPV formulė 1

Palikite pradines išlaidas už reikšmių intervalo ribų ir atimkite jas iš NPV funkcijos rezultato. Kadangi pradinės išlaidos paprastai įvedamos kaip neigiamas skaičius , iš tikrųjų atliekate sudėties operaciją:

Šiuo atveju "Excel" NPV funkcija tiesiog grąžina dabartinę nelygių pinigų srautų vertę. Kadangi norime gauti "grynąją" (t. y. dabartinę būsimųjų pinigų srautų vertę, atėmus pradines investicijas), pradines sąnaudas atimame už NPV funkcijos ribų.

"Excel" NPV formulė 2

Į verčių intervalą įtraukite pradines išlaidas ir rezultatą padauginkite iš (1 + norma).

Šiuo atveju "Excel" NPV funkcija pateiktų -1 laikotarpio rezultatą (tarsi pradinė investicija būtų atlikta vienu laikotarpiu prieš 0 laikotarpį), turime padauginti jos rezultatą iš (1 + r), kad NPV būtų perkelta vienu laikotarpiu į priekį (t. y. nuo i = -1 iki i = 0). Žr. glaustą NPV formulės formą.

Kurią formulę naudoti, priklauso nuo jūsų asmeninių pageidavimų. Aš asmeniškai manau, kad pirmoji formulė yra paprastesnė ir lengviau suprantama.

NPV skaičiuoklė "Excel" programoje

Dabar pažiūrėkime, kaip galite naudoti pirmiau pateiktas formules tikriesiems duomenims ir sukurti savo NPV skaičiuoklę "Excel" programoje.

Tarkime, kad turite pradines išlaidas B2, būsimųjų pinigų srautų eilutę B3:B7 ir reikalaujamą grąžos normą F1. Norėdami rasti grynąją dabartinę vertę, naudokite vieną iš šių formulių:

NPV formulė 1:

=NPV(F1, B3:B7) + B2

Atkreipkite dėmesį, kad pirmasis vertės argumentas yra 1 laikotarpio pinigų srautas (B3), o pradinės sąnaudos (B2) neįtrauktos.

2 NPV formulė:

=NPV(F1, B2:B7) * (1+F1)

Šioje formulėje į verčių intervalą įtraukiamos pradinės išlaidos (B2).

Toliau pateiktoje ekrano nuotraukoje parodyta veikianti "Excel" NPV skaičiuoklė:

Norėdami įsitikinti, kad mūsų "Excel" NPV formulės yra teisingos, patikrinkime rezultatą atlikdami skaičiavimus rankiniu būdu.

Pirmiausia, naudodami pirmiau aptartą PV formulę, nustatome kiekvieno pinigų srauto dabartinę vertę:

=B3/(1+$F$1)^A3

Tuomet susumuokite visas dabartines vertes ir atimkite pradines investicijų sąnaudas:

=SUMA(C3:C7)+B2

... ir pamatysite, kad visų trijų formulių rezultatai yra visiškai vienodi.

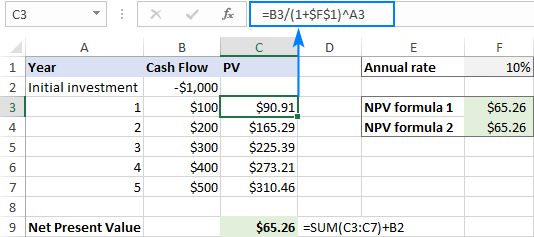
Pastaba. Šiame pavyzdyje kalbama apie metinius pinigų srautus ir metinę normą. Jei norite rasti ketvirčio arba kas mėnesį grynąją dabartinę vertę "Excel" programoje, būtinai atitinkamai pakoreguokite diskonto normą, kaip paaiškinta šiame pavyzdyje.

PV ir NPV skirtumas programoje "Excel

Finansų srityje tiek PV, tiek NPV naudojamos būsimųjų pinigų srautų dabartinei vertei įvertinti, diskontuojant būsimas sumas iki dabarties. Tačiau jos skiriasi vienu svarbiu aspektu:

• Dabartinė vertė (PV) - tai visos būsimos pinigų įplaukos tam tikru laikotarpiu.
• Grynoji dabartinė vertė (NPV) - tai pinigų įplaukų dabartinės vertės ir pinigų išplaukų dabartinės vertės skirtumas.

Kitaip tariant, PV atsižvelgia tik į pinigų įplaukas, o NPV atsižvelgia ir į pradines investicijas arba išlaidas, todėl tai yra grynasis skaičius.

Programoje "Microsoft Excel" funkcijos skiriasi dviem esminiais aspektais:

• NPV funkcija gali apskaičiuoti nevienodus (kintamus) pinigų srautus. PV funkcija reikalauja, kad pinigų srautai būtų pastovūs per visą investicijos laikotarpį.
• Naudojant NPV, pinigų srautai turi atsirasti kiekvieno laikotarpio pabaigoje. PV gali apdoroti pinigų srautus, atsirandančius laikotarpio pabaigoje ir pradžioje.

NPV ir XNPV skirtumas programoje "Excel

XNPV - tai dar viena "Excel" finansinė funkcija, kuri apskaičiuoja grynąją dabartinę investicijos vertę. Pagrindinis šių funkcijų skirtumas yra toks:

• NPV mano, kad visi laikotarpiai yra vienodai .
• XNPV leidžia nurodyti datas, atitinkančias kiekvieną pinigų srautą. Dėl šios priežasties XNPV funkcija yra daug tikslesnė, kai dirbama su pinigų srautų serijomis. nereguliarūs intervalai .

Kitaip nei NPV, "Excel" XNPV funkcija įgyvendinama "paprastai" - pirmoji vertė atitinka investicijų pradžioje atsirandantį pinigų srautą. Visi vėlesni pinigų srautai diskontuojami remiantis 365 dienų metais.

Sintaksės požiūriu XNPV funkcija turi vieną papildomą argumentą:

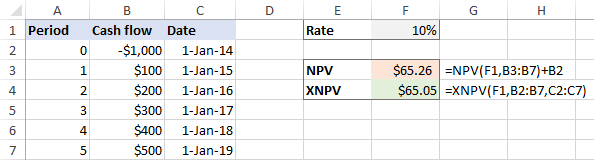
Pavyzdžiui, naudokime abi funkcijas tam pačiam duomenų rinkiniui, kuriame F1 yra diskonto norma, B2:B7 - pinigų srautai, o C2:C7 - datos:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

Jei pinigų srautai yra platinamas tolygiai investuojant, NPV ir XNPV funkcijos duoda labai artimus skaičius:

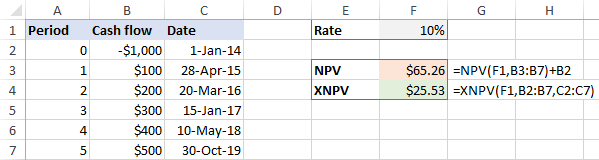
Jei nereguliarūs intervalai , skirtumas tarp rezultatų yra labai didelis:

Dažniausiai pasitaikančios klaidos apskaičiuojant grynąją dabartinę vertę "Excel" programoje

Dėl gana specifinio NPV funkcijos įgyvendinimo apskaičiuojant grynąją dabartinę vertę "Excel" programoje daroma daug klaidų. Toliau pateikiami paprasti pavyzdžiai rodo tipiškiausias klaidas ir kaip jų išvengti.

Nereguliarūs intervalai

"Excel" NPV funkcija daro prielaidą, kad visi pinigų srautų laikotarpiai yra vienodai . Jei pateiksite skirtingus intervalus, tarkime, metus ir ketvirčius ar mėnesius, grynoji dabartinė vertė bus neteisinga dėl nesuderintų laikotarpių.

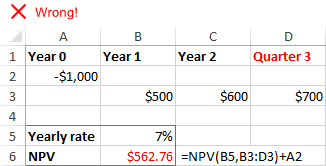
Trūkstami laikotarpiai arba pinigų srautai

"Excel" programa NPV neatpažįsta praleistų laikotarpių ir ignoruoja tuščius langelius. Kad NPV būtų apskaičiuota teisingai, būtinai pateikite iš eilės mėnesių, ketvirčių arba metų ir pasiūla nulis reikšmės laikotarpiams, kurių pinigų srautai yra nuliniai.

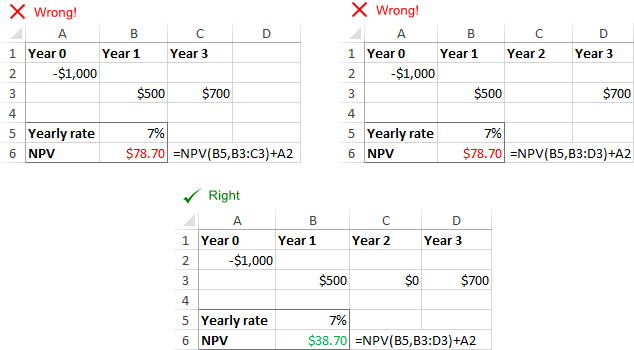
Diskonto norma neatitinka faktinių laikotarpių

"Excel" NPV funkcija negali automatiškai pritaikyti pateiktos normos prie duoto laiko dažnumo, pavyzdžiui, metinės diskonto normos prie mėnesio pinigų srautų. Naudotojas privalo pateikti atitinkama norma už laikotarpį .

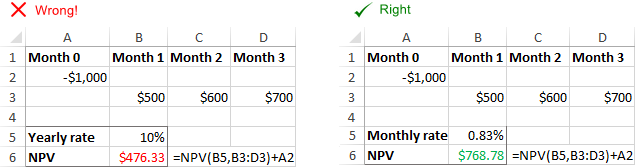
Neteisingas normos formatas

Diskonto arba palūkanų norma turi būti pateikta kaip procentinė dalis arba atitinkama dešimtainis skaičius . Pavyzdžiui, 10 proc. normą galima pateikti kaip 10 % arba 0,1. Jei normą įvesite kaip skaičių 10, "Excel" ją traktuos kaip 1000 %, ir NPV bus apskaičiuota neteisingai.

Štai kaip "Excel" programoje naudoti NPV, kad rastumėte investicijos grynąją dabartinę vertę. Jei norite atidžiau susipažinti su šiame vadovėlyje aptartomis formulėmis, nedvejodami atsisiųskite mūsų pavyzdinę "Excel" skirtą NPV skaičiuoklę.

Dėkojame, kad skaitote, ir tikimės, kad kitą savaitę susitiksime mūsų tinklaraštyje!