Yn dizze tutorial sille jo leare hoe't jo de Excel NPV-funksje brûke om de netto hjoeddeistige wearde fan in ynvestearring te berekkenjen en hoe't jo gewoane flaters kinne foarkomme as jo NPV dogge yn Excel.

Netto hjoeddeistige wearde of netto hjoeddeistige wearde is in kearn elemint fan finansjele analyze dat oanjout oft in projekt rendabel sil wêze of net. Wêrom is de netto hjoeddeistige wearde sa wichtich? Om't de basis finansjele konsept hâldt dat jild dat mooglik kin wurde ûntfongen yn 'e takomst minder wurdich is as itselde bedrach fan jild dat jo no hawwe. Netto hjoeddeistige wearde ferminderet de cashflows dy't yn 'e takomst ferwachte wurde werom nei it hjoeddeiske om har hjoeddeistige wearde te sjen.

Microsoft Excel hat in spesjale funksje foar it berekkenjen fan NPV, mar it gebrûk kin lestich wêze foaral foar minsken dy't net folle ûnderfining hawwe. yn finansjele modellering. It doel fan dit artikel is om jo sjen te litten hoe't de Excel NPV-funksje wurket en mooglike falkûlen oanwize by it berekkenjen fan de netto hjoeddeistige wearde fan in searje cashflows yn Excel.

Wat is net hjoeddeiske wearde (NPV)?

Netto hjoeddeiske wearde (NPV) is de wearde fan in searje cashflows oer it hiele libben fan in projekt ôfkoarte oant no.

Yn ienfâldige termen kin NPV definiearre wurde as de hjoeddeiske wearde fan takomstige cashflows minus de initial ynvestearringskosten:

NPV = PV fan takomstige cashflows – Initial Investment

Om better begripe deperioaden dy't nul cashflows hawwe.

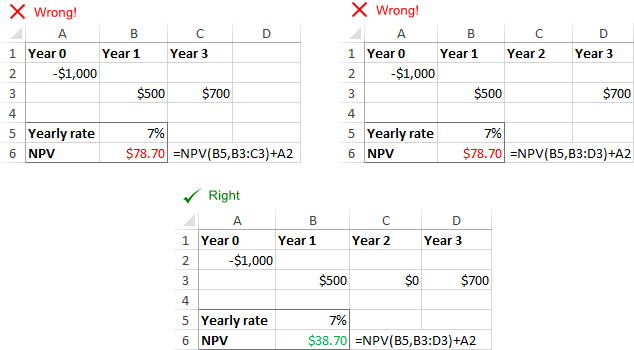
Discounttaryf komt net oerien mei werklike tiidperioaden

De Excel NPV-funksje kin it levere taryf net oanpasse oan de opjûne tiid frekwinsjes automatysk, bygelyks jierlikse koarting taryf oan moanlikse cash flows. It is de ferantwurdlikens fan de brûker om in passende taryf per perioade oan te jaan.

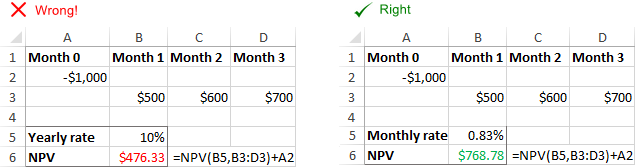
Ferkearde taryfopmaak

De koarting of rintepersintaazje moat wêze opjûn as in persintaazje of oerienkommende desimale getal . Bygelyks, it taryf fan 10 prosint kin wurde levere as 10% of 0,1. As jo ​​it taryf as nûmer 10 ynfiere, sil Excel it behannelje as 1000%, en NPV wurdt ferkeard berekkene.

Dat is hoe't jo NPV yn Excel brûke om it net te finen hjoeddeistige wearde fan in ynvestearring. Om in tichterby te sjen nei de formules dy't yn dit lesboek besprutsen binne, fiel jo frij om ús foarbyld NPV rekkenmasine foar Excel te downloaden.

Tankewol foar it lêzen en hoopje jo nije wike op ús blog te sjen!

Foar in inkele cashflow wurdt hjoeddeiske wearde (PV) berekkene mei dizze formule:

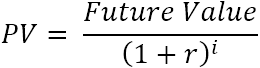
Wêr :

• r – koarting of rinte
• i – de cashflowperioade

Bygelyks om $110 (takomstige wearde) nei 1 jier te krijen (ik), hoefolle moatte jo hjoed ynvestearje yn jo bankrekken dy't 10% jierlikse rinte (r) biedt? De boppesteande formule jout dit antwurd:

$110/(1+10%)^1 = $100

Mei oare wurden, $100 is de hjoeddeiske wearde fan $110 dy't ferwachte wurde te ûntfangen yn 'e takomst.

Netto hjoeddeistige wearde (NPV) foeget de hjoeddeistige wearden op fan alle takomstige cashflows om se op in inkeld punt yn it hjoeddeiske te bringen. En om't it idee fan "netto" is om sjen te litten hoe rendabel it projekt sil wêze nei it rekkenjen fan 'e inisjele kapitaalynvestearring dy't nedich is om it te finansieren, wurdt it bedrach fan' e earste ynvestearring subtrahearre fan 'e som fan alle hjoeddeistige wearden:

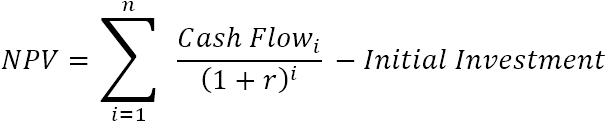
Wêr:

• r – koarting of rinte
• n – it oantal tiidperioaden
• i – de cash flow perioade

Om't elk net-nul nûmer ferhege nei de nulmacht is gelyk oan 1, kinne wy ​​​​de earste ynvestearring yn 'e som opnimme. Tink derom dat yn dizze kompakte ferzje fan 'e NPV-formule, i=0, d.w.s. de earste ynvestearring wurdt makke yn perioade 0.

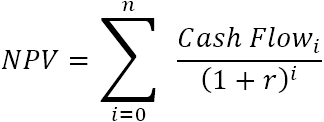
Bygelyks, om NPV te finen foar in searje cashflows (50, 60, 70) koarting op 10% en de inisjele kosten fan$ 100, kinne jo dizze formule brûke:

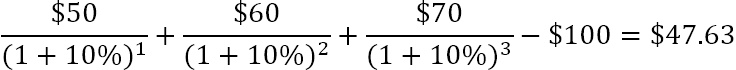
Of

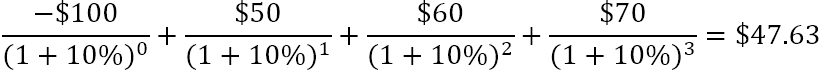
Hoe helpt de netto hjoeddeistige wearde by it evaluearjen fan in finansjeel leefberens fan in foarnommen ynvestearring? Der wurdt fan útgien dat in ynvestearring mei in positive NPV rendabel is, en in ynvestearring mei in negative NPV sil net rendabel wêze. Dit konsept is de basis fan 'e Net Present Value Rule , dy't seit dat jo allinich meidwaan moatte oan projekten mei in positive netto hjoeddeistige wearde.

Excel NPV-funksje

De NPV-funksje yn Excel jout de netto hjoeddeistige wearde fan in ynvestearring werom op basis fan in koarting of rinte en in searje takomstige cashflows.

De syntaksis fan de Excel NPV-funksje is as folget:

Wêr:

• Taryf (ferplicht) - de koarting of rintepersintaazje oer ien perioade. It moat oanjûn wurde as persintaazje of in oerienkommende desimaal getal.
• Wearde1, [wearde2], … - numerike wearden dy't in searje reguliere cashflows fertsjintwurdigje. Wearde1 is fereaske, folgjende wearden binne opsjoneel. Yn 'e moderne ferzjes fan Excel 2007 oant 2019 kinne oant 254 weardearguminten wurde levere; yn Excel 2003 en âlder - oant 30 arguminten.

De NPV-funksje is beskikber yn Excel 365 - 2000.

Tips:

• Om te berekkenjen hjoeddeiske wearde fan annuïteit, brûk Excel PV-funksje.
• Om in projektearre rendemint op ynvestearring te skatten, doch de IRR-berekkening.

4 dingen dy't jomoatte witte oer NPV-funksje

Om te soargjen dat jo NPV-formule yn Excel korrekt berekkent, hâld asjebleaft dizze feiten yn gedachten:

• Wearden moatte foarkomme oan it ein fan elke perioade . As de earste cashflow (earste ynvestearring) foarkomt oan it begjin fan 'e earste perioade , brûk dan ien fan dizze NPV-formules.
• Wearden moatte oanjûn wurde yn gronologyske folchoarder en lyk ferdield yn tiid .
• Brûk negative wearden om útstreamen te fertsjintwurdigjen (útbetelle cash) en positive wearden om ynstreamen te fertsjintwurdigjen (ûntfongen cash ).
• Allinnich numerike wearden wurde ferwurke. Lege sellen, tekstfoarstellings fan sifers, logyske wearden en flaterwearden wurde negearre.

Hoe't Excel NPV-funksje wurket

It brûken fan de NPV-funksje yn Excel is in bytsje lestich fanwegen de manier wêrop de funksje wurdt útfierd. Standert wurdt oannommen dat in ynvestearring ien perioade makke wurdt foar de wearde1 datum. Om dizze reden wurket in NPV-formule yn syn suvere foarm allinich krekt as jo de inisjele ynvestearringskosten leverje ien perioade fan no , net hjoed!

Om dit te yllustrearjen, litte wy de netto hjoeddeistige wearde berekkenje hânmjittich en mei in Excel NPV-formule, en fergelykje de resultaten.

Litte wy sizze, jo hawwe in koartingsnivo yn B1, in rige cashflows yn B4:B9 en perioadenûmers yn A4:A9.

Leverje de boppesteande referinsjes yn dizze generike PV-formule:

PV = takomstwearde/(1+rate)^period

En jo krije de folgjende fergeliking:

=B4/(1+$B$1)^A4

Dizze formule giet nei C4 en wurdt dan kopiearre nei de ûndersteande sellen. Troch it tûke gebrûk fan absolute en relative selferwizings past de formule perfekt oan foar elke rige lykas werjûn yn 'e skermôfdruk hjirûnder.

Tink derom dat wy de hjoeddeistige wearde fan 'e earste ynvestearring ek berekkenje sûnt de earste ynvestearringskosten is nei 1 jier , dus it wurdt ek fermindere.

Dêrnei sommje wy alle hjoeddeiske wearden op:

=SUM(C4:C9)

En no litte wy do NPV mei de Excel-funksje:

=NPV(B1, B4:B9)

Sa't jo sjen kinne, komme de resultaten fan beide berekkeningen krekt oerien:

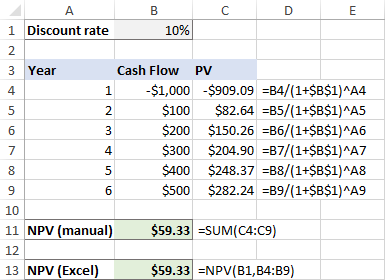
Mar wat as de inisjele útjefte foarkomt oan it begjin fan 'e earste perioade , sa't it typysk docht?

Om't de earste ynvestearring hjoed wurdt makke, jildt der gjin koarting foar, en foegje wy dit bedrach gewoan ta oan 'e som fan' e hjoeddeistige wearden fan takomstige cashflows (om't it in negatyf getal is, wurdt it eins subtrahearre):

=SUM(C4:C9)+B4

En yn dit gefal jouwe de hânberekkening en Excel NPV-funksje opbringst ferskillende resultaten:

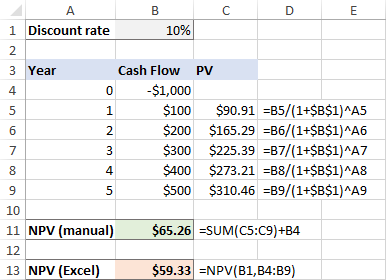
Betsjut dit dat wy net kinne fertrouwe op de NPV foar mula yn Excel en moatte yn dizze situaasje de netto hjoeddeistige wearde manuell berekkenje? Fansels net! Jo sille gewoan de NPV-funksje in bytsje moatte oanpasse lykas útlein yn 'e folgjende paragraaf.

Hoe kinne jo NPV yn Excel berekkenje

As de earste ynvestearringwurdt makke oan it begjin fan 'e earste perioade , kinne wy ​​​​it behannelje as in cashflow oan 'e ein fan' e foarige perioade (dus perioade 0). Mei dat yn gedachten binne d'r twa ienfâldige manieren om NPV yn Excel te finen.

Excel NPV-formule 1

Lit de begjinkosten bûten it berik fan wearden en subtract it fan it resultaat fan 'e NPV-funksje . Om't de inisjele útjefte typysk wurdt ynfierd as in negatyf getal , fiere jo de tafoegingsoperaasje eins út:

Yn dit gefal komt de Excel NPV-funksje gewoan werom de hjoeddeiske wearde fan ûngelikense cashflows. Om't wy "netto" wolle (d.w.s. hjoeddeistige wearde fan takomstige cashflows minder initial ynvestearring), subtrahearje wy de begjinkosten bûten de NPV-funksje. yn it berik fan wearden en fermannichfâldigje it resultaat mei (1 + taryf).

Yn dit gefal soe de Excel NPV-funksje jo it resultaat jaan fan perioade -1 (as soe de earste ynvestearring ien perioade makke wurde foar perioade 0), moatte wy de útfier fermannichfâldigje mei (1 + r) om de NPV ien perioade yn 'e tiid foarút te bringen (dus fan i = -1 nei i = 0). Sjoch asjebleaft de kompakte foarm fan de NPV-formule.

Hokker formule te brûken is in kwestje fan jo persoanlike foarkar. Ik persoanlik leau dat de earste ienfâldiger en makliker te begripen is.

NPV rekkenmasine yn Excel

Lit no sjen hoe't jo it boppesteande brûke kinneformules op echte gegevens om jo eigen NPV rekkenmasine yn Excel te meitsjen.

Stel dat jo de earste útjeften hawwe yn B2, in searje takomstige cashflows yn B3:B7, en de fereaske weromfertsjintiid yn F1. Om NPV te finen, brûk ien fan 'e folgjende formules:

NPV-formule 1:

=NPV(F1, B3:B7) + B2

Let op dat it earste weardeargumint de cash is stream yn perioade 1 (B3), de begjinkosten (B2) binne net opnommen.

NPV Formule 2:

=NPV(F1, B2:B7) * (1+F1)

Dizze formule befettet de begjinkosten (B2) yn it berik fan wearden.

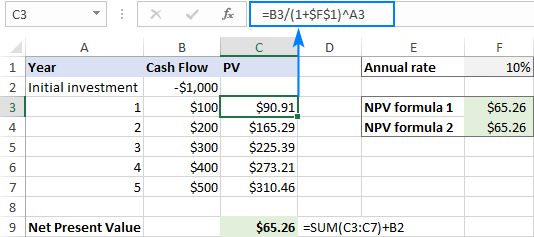
De ûndersteande skermôfbylding lit ús Excel NPV rekkenmasine yn aksje sjen:

Om derfoar te soargjen dat ús Excel NPV formules goed binne, lit ús it resultaat kontrolearje mei hânmjittige berekkeningen.

Earst fine wy ​​de hjoeddeiske wearde fan elke cashflow troch de hjirboppe besprutsen PV-formule te brûken:

=B3/(1+$F$1)^A3

Folgjende, tel alle hjoeddeistige wearden op en subtract de earste kosten fan ynvestearring:

=SUM(C3:C7)+B2

... en sjoch dat de resultaten fan alle trije formules absolút itselde binne.

Opmerking. Yn dit foarbyld hawwe wy te krijen mei jierlikse cashflows en jierlikse taryf. As jo ​​ fjirdeliks of moanlikse NPV fine yn Excel, wês der wis fan dat jo it koartingsnivo dêroer oanpasse lykas útlein yn dit foarbyld.

Ferskil tusken PV en NPV yn Excel

Yn finânsjes wurde sawol PV as NPV brûkt om de aktuele wearde fan takomstige cashflows te mjitten troch takomstige bedraggen te koartsjen nei it hjoeddeiske. Marse ferskille op ien wichtige manier:

• Tsjintwurdich wearde (PV) - ferwiist nei alle takomstige cashynstreamen yn in bepaalde perioade.
• Netto oanwêzich wearde (NPV) - is it ferskil tusken de hjoeddeiske wearde fan cash ynstreamen en de hjoeddeiske wearde fan cash outflows.

Mei oare wurden, PV jout allinnich rekken foar cash ynstreamen, wylst NPV ek rekkens foar de earste ynvestearring of útjefte, wêrtroch it in netto figuer is.

Yn Microsoft Excel binne d'r twa essensjele ferskillen tusken de funksjes:

• De NPV-funksje kin ûngelikense (fariabele) berekkenje. jildstreamen. De PV-funksje fereasket dat cashflows konstant binne oer it hiele libben fan in ynvestearring.
• Mei NPV moatte cashflows oan 'e ein fan elke perioade foarkomme. PV kin omgean cashflows dy't foarkomme oan 'e ein en oan it begjin fan in perioade.

Ferskil tusken NPV en XNPV yn Excel

XNPV is ien mear Excel finansjele funksje dy't berekkent de netto hjoeddeistige wearde fan in ynvestearring. It primêre ferskil tusken de funksjes is as folget:

• NPV achtet alle tiidperioaden lykweardich te wêzen.
• XNPV lit jo datums opjaan dy't oerienkomme mei elk jildstream. Om dizze reden is de XNPV-funksje folle krekter by it omgean mei in searje cashflows op unregelmjittige yntervallen .

Oars as NPV, wurdt de Excel XNPV-funksje "normaal ymplementearre" " - de earste wearde komt oerien mei de útstream dy't optreedt byit begjin fan 'e ynvestearring. Alle opienfolgjende cashflows wurde fermindere op basis fan in jier fan 365 dagen.

Op syntaksis hat de XNPV-funksje ien ekstra argumint:

As foarbyld , lit ús beide funksjes brûke op deselde dataset, wêrby't F1 it koartingsnivo is, B2:B7 cashflows binne en C2:C7 datums binne:

=NPV(F1,B3:B7)+B2

=XNPV(F1,B2:B7,C2:C7)

As de cashflows ferdield lykmjittich binne troch de ynvestearring, jouwe de NPV- en XNPV-funksjes tige tichte sifers werom:

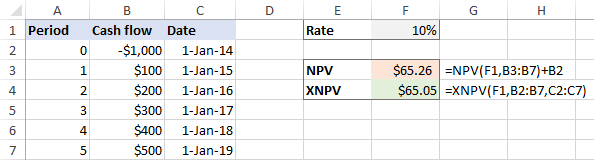
In gefal fan unregelmjittige yntervallen , it ferskil tusken de resultaten is tige wichtich:

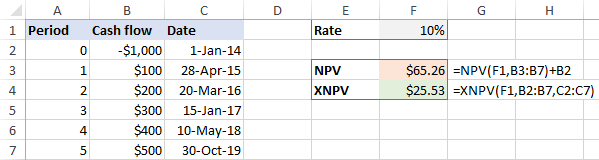
Algemiene flaters by it berekkenjen fan NPV yn Excel

Om't in frij spesifike ymplemintaasje fan 'e NPV-funksje, in protte flaters wurde makke by it berekkenjen fan netto hjoeddeistige wearde yn Excel. De ienfâldige foarbylden hjirûnder litte de meast typyske flaters sjen en hoe't se har foarkomme.

Unregelmjittige yntervallen

De Excel NPV-funksje giet derfan út dat alle cashflowperioaden lykweardich binne . As jo ​​​​ferskillende yntervallen leverje, sis mar jierren en kertieren of moannen, sil de netto hjoeddeistige wearde ferkeard wêze fanwege net-koherinte tiidperioaden.

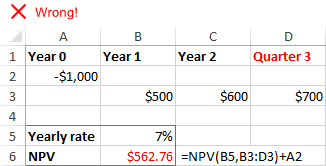
Ontbrekkende perioaden of cashflows

NPV yn Excel herkent net oerlitten perioaden en negearret lege sellen. Om de NPV korrekt te berekkenjen, wês asjebleaft der wis fan dat jo opfolgjende moannen, kwartalen of jierren leverje en nul wearden foar tiid leverje