Az oktatóanyag bemutatja, hogyan lehet kiszámítani egy projekt belső megtérülési rátáját Excelben képletek és a Célkeresés funkció segítségével. Azt is megtanulja, hogyan hozhat létre egy belső megtérülési ráta sablont, hogy az összes IRR-számítást automatikusan elvégezze.

Ha ismeri egy javasolt befektetés belső megtérülési rátáját, azt gondolhatja, hogy már minden megvan az értékeléshez - minél nagyobb az IRR, annál jobb. A gyakorlatban ez nem ilyen egyszerű. A Microsoft Excel három különböző funkciót biztosít a belső megtérülési ráta meghatározásához, és nagyon hasznos, ha valóban megérti, hogy valójában mit is számol az IRR-rel.

Mi az IRR?

A belső megtérülési ráta (IRR) egy általánosan használt mérőszám egy potenciális befektetés jövedelmezőségének becslésére. Néha úgy is nevezik, mint diszkontált cash flow ráta a visszatérés vagy gazdasági megtérülési ráta .

Technikailag az IRR az a diszkontráta, amely egy adott befektetésből származó összes pénzáramlás (mind a beáramló, mind a kiáramló) nettó jelenértékét nullával teszi egyenlővé.

A "belső" kifejezés azt jelzi, hogy az IRR csak belső tényezőket vesz figyelembe; a külső tényezőket, például az inflációt, a tőkeköltséget és a különböző pénzügyi kockázatokat kizárják a számításból.

Mit mutat az IRR?

A tőkeköltségvetésben az IRR-t széles körben használják egy leendő beruházás jövedelmezőségének értékelésére és több projekt rangsorolására. Az általános elv ilyen egyszerű: minél magasabb a belső megtérülési ráta, annál vonzóbb a projekt.

Egyetlen projekt becslésekor a pénzügyi elemzők jellemzően az IRR-t hasonlítják össze a vállalkozás súlyozott átlagos tőkeköltség vagy akadályviszonylati ráta Egy hipotetikus helyzetben, amikor az IRR az egyetlen kritérium a döntés meghozatalához, egy projekt akkor tekinthető jó befektetésnek, ha az IRR nagyobb, mint a küszöbráta. Ha az IRR kisebb, mint a tőkeköltség, a projektet el kell utasítani. A gyakorlatban számos más tényező is befolyásolja az IRR-t.döntés, mint például a nettó jelenérték (NPV), a megtérülési idő, az abszolút megtérülési érték stb.

IRR korlátozások

Bár az IRR nagyon népszerű módszer a tőkeprojektek értékelésére, számos olyan hibája van, amelyek nem optimális döntésekhez vezethetnek. Az IRR fő problémái a következők:

• Relatív mérték Az IRR a százalékos arányt veszi figyelembe, de nem az abszolút értéket, és ennek eredményeként előnyben részesíthet egy magas megtérülési rátájú, de nagyon kis dollárértékű projektet. A gyakorlatban a vállalatok előnyben részesíthetnek egy kisebb IRR-rel rendelkező nagy projektet egy nagyobb IRR-rel rendelkező kicsivel szemben. Ebben a tekintetben az NPV jobb mérőszám, mivel a projekt vállalásával ténylegesen nyert vagy elvesztett összeget veszi figyelembe.
• Ugyanaz az újrabefektetési ráta Az IRR feltételezi, hogy a projekt által generált összes pénzáramlást az IRR-rel megegyező arányban fektetik be újra, ami nagyon irreális forgatókönyv. Ezt a problémát a MIRR oldja meg, amely lehetővé teszi különböző finanszírozási és újrabefektetési arányok megadását.
• Több eredmény A váltakozó pozitív és negatív pénzáramlású projektek esetében egynél több IRR-t lehet találni. A kérdés megoldódik a MIRR-ben is, amely úgy van kialakítva, hogy csak egy rátát adjon.

E hiányosságok ellenére az IRR továbbra is fontos mérőszáma a tőkeköltségvetésnek, és legalábbis érdemes szkeptikusan megnézni, mielőtt befektetési döntést hozunk.

IRR-számítás Excelben

Mivel a belső megtérülési ráta az a diszkontráta, amely mellett egy adott pénzáramlási sorozat nettó jelenértéke nulla, az IRR-számítás a hagyományos NPV-képleten alapul:

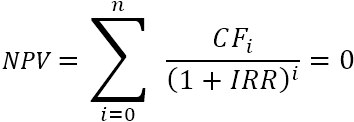
Ha nem nagyon ismeri az összegző jelölést, az IRR-képlet kibővített formája könnyebben érthető:

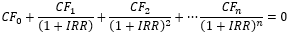
Hol:

• CF ₀ - a kezdeti befektetés (negatív számmal jelezve)
• CF ₁ , CF ₂ .... CF _n - pénzáramlások
• i - az időszak száma
• n - időszakok összesen
• IRR - belső megtérülési ráta

A képlet jellege miatt nincs analitikus módszer az IRR kiszámítására. A "találgatás és ellenőrzés" módszerét kell alkalmaznunk a kiszámításához. A belső megtérülési ráta fogalmának jobb megértéséhez végezzünk IRR-számítást egy nagyon egyszerű példán.

Példa : 1000 dollárt fektet be most, és a következő 2 évben 500 és 660 dollárt kap vissza. Milyen diszkontrátával lesz a nettó jelenérték nulla?

Első tippként próbáljuk ki a 8%-os arányt:

• Most: PV = -$1,000
• 1. év: PV = $500 / (1+0,08)1 = $462,96
• 2. év: PV = $660 / (1+0,08)2 = $565,84

Ezeket összeadva megkapjuk a NPV 28,81 dollárral egyenlő:

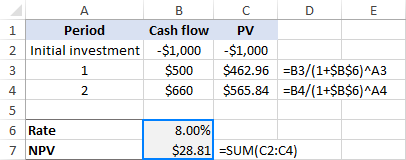
Ó, közel sem 0. Talán egy jobb becslés, mondjuk 10%, megváltoztathatja a dolgokat?

• Most: PV = -$1,000
• 1. év: PV = $500 / (1+0,1)1 = $454,55
• 2. év: PV = $660 / (1+0,1)2 = $545,45
• NPV: -1000 + $454.55 + $545.45 = $0.00

Ez az! 10%-os diszkontráta mellett az NPV pontosan 0. Tehát a befektetés IRR-je 10%:

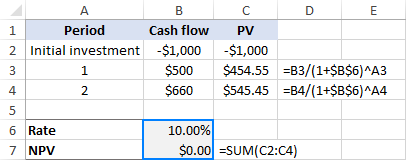
Így számítja ki a belső megtérülési rátát kézzel. A Microsoft Excel, más szoftverek és különböző online IRR-kalkulátorok is erre a próbálgatásos módszerre támaszkodnak. De az emberekkel ellentétben a számítógépek nagyon gyorsan képesek többszörös ismétléseket végezni.

Az IRR kiszámítása Excelben képletekkel

A Microsoft Excel 3 funkciót biztosít a belső megtérülési ráta meghatározásához:

• IRR - a leggyakrabban használt függvény a belső megtérülési ráta kiszámítására egy sor olyan pénzáramlásra vonatkozóan, amely a következő időpontokban történik rendszeres időközönként .
• XIRR - az IRR-t olyan pénzáramlások sorozatára találja meg, amelyek a következő időpontokban következnek be szabálytalan időközök Mivel figyelembe veszi a kifizetések pontos dátumát, ez a funkció jobb számítási pontosságot biztosít.
• MIRR - visszaadja a módosított belső megtérülési ráta , amely az IRR egy olyan változata, amely figyelembe veszi mind a hitelfelvételi költséget, mind a pozitív cash flow-k újrabefektetése után kapott kamatos kamatot.

Az alábbiakban mindezen függvényekre talál példákat. A következetesség kedvéért minden képletben ugyanazt az adatkészletet fogjuk használni.

IRR képlet a belső megtérülési ráta kiszámításához

Tegyük fel, hogy egy 5 éves befektetést tervezünk a B2:B7 pénzáramlásokkal. Az IRR kiszámításához használjuk az alábbi egyszerű képletet:

=IRR(B2:B7)

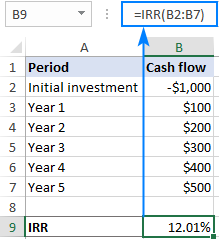
Megjegyzés: Ahhoz, hogy az IRR-képlet helyesen működjön, kérjük, győződjön meg arról, hogy a pénzáramlásoknak legalább egy negatív (kiáramlás) és egy pozitív érték (beáramlás), és az összes értéket az alábbi listán kell feltüntetni időrendi sorrend .

További információért lásd az Excel IRR funkcióját.

XIRR képlet az IRR kiszámításához szabálytalan pénzáramlások esetén

Az egyenlőtlen időzítésű pénzáramlások esetén az IRR függvény használata kockázatos lehet, mivel feltételezi, hogy minden kifizetés az időszak végén történik, és minden időszak egyenlő. Ebben az esetben az XIRR bölcsebb választás lenne.

A B2:B7-ben szereplő pénzáramlások és a C2:C7-ben szereplő dátumok esetén a képlet a következőképpen néz ki:

=XIRR(B2:B7,C2:C7)

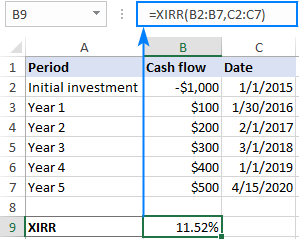
Megjegyzések:

• Bár az XIRR funkció nem feltétlenül követeli meg a dátumokat időrendi sorrendben, az első pénzáramlás (kezdeti befektetés) dátumának kell az első helyen állnia a tömbben.
• A dátumokat a következő formában kell megadni érvényes Excel dátumok ; a szöveges formátumú dátumok megadása az Excel számára a félreértelmezés kockázatát jelenti.
• Az Excel XIRR függvénye más képletet használ az eredmény eléréséhez. Az XIRR képlet a 365 napos év alapján diszkontálja a későbbi kifizetéseket, ennek eredményeképpen az XIRR mindig a következő értéket adja vissza évesítve belső megtérülési ráta.

További részletekért lásd az Excel XIRR funkcióját.

MIRR-képlet a módosított IRR kiszámításához

Egy reálisabb helyzet kezelésére, amikor a projekt pénzeszközeit a vállalat tőkeköltségéhez közelebbi arányban fektetik be újra, a módosított belső megtérülési rátát a MIRR-képlet segítségével lehet kiszámítani:

=MIRR(B2:B7,E1,E2)

Ahol B2:B7 a pénzáramlások, E1 a finanszírozási kamatláb (a pénzfelvétel költsége) és E2 az újrabefektetési kamatláb (a nyereség újrabefektetése után kapott kamat).

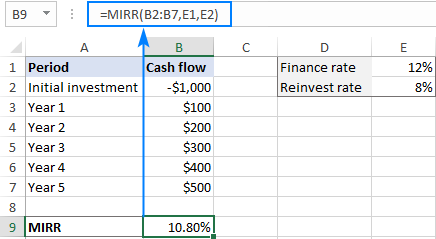
Megjegyzés: Mivel az Excel MIRR függvénye a nyereségre vonatkozó kamatos kamatot számítja ki, az eredménye lényegesen eltérhet az IRR és XIRR függvények eredményétől.

IRR, XIRR és MIRR - melyik a jobb?

Úgy vélem, senki sem tud általános választ adni erre a kérdésre, mivel mindhárom módszer elméleti alapja, előnyei és hátrányai még mindig vitatottak a pénzügyi szakemberek között. Talán a legjobb megközelítés az lenne, ha mindhárom számítást elvégeznénk, és összehasonlítanánk az eredményeket:

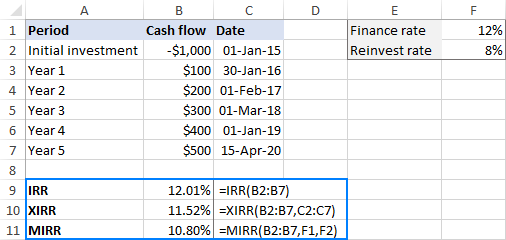
Általában úgy tekintik, hogy:

• Az XIRR jobb számítási pontosságot biztosít, mint az IRR, mivel figyelembe veszi a pénzáramlások pontos időpontjait.
• Az IRR gyakran indokolatlanul optimista értékelést ad a projekt jövedelmezőségéről, míg a MIRR reálisabb képet ad.

IRR kalkulátor - Excel sablon

Ha rendszeresen kell IRR-számításokat végeznie Excelben, egy belső megtérülési ráta sablon beállítása nagyban megkönnyítheti az életét.

Számológépünk mindhárom képletet (IRR, XIRR és MIRR) tartalmazza, így nem kell aggódnia, hogy melyik eredmény az érvényesebb, hanem mindegyiket figyelembe veheti.

1. Írja be a pénzáramlásokat és a dátumokat két oszlopba (esetünkben az A és a B oszlopba).
2. Adja meg a finanszírozási rátát és az újrabefektetési rátát 2 külön cellában. Opcionálisan nevezze el ezeket az eladásokat. Finance_rate és Reinvest_rate illetve.
3. Hozzon létre két dinamikusan definiált tartományt, amelyek neve Cash_flows és Dátumok .

   Feltételezve, hogy a munkalap neve Sheet1 , az első pénzáramlás (kezdeti befektetés) az A2 cellában van, az első pénzáramlás dátuma pedig a B2 cellában, készítse el a megnevezett tartományokat e képletek alapján:

   Lásd még: Hogyan ossza meg az Outlook naptárat a Google-lal

   Cash_flows:

   =OFFSET(Sheet1!$A$2,0,0,0,COUNT(Sheet1!$A:$A),1)

   Időpontok:

   =OFFSET(Sheet1!$B$2,0,0,0,COUNT(Sheet1!$B:$B),1)

   A részletes lépéseket a Hogyan hozzunk létre dinamikus névtartományt az Excelben című fejezetben találja.

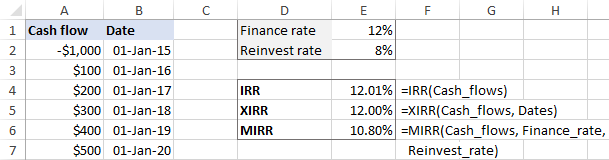
4. Használja az imént létrehozott neveket a következő képletek argumentumaiként. Vegye figyelembe, hogy a képletek bármelyik oszlopba beírhatók, kivéve az A és B oszlopokat, amelyek kizárólag a pénzáramlásoknak, illetve a dátumoknak vannak fenntartva.

   =IRR(Cash_flows)

   =XIRR(Cash_flows, Dátumok)

   =MIRR(Cash_flows, Finance_rate, Reinvest_rate)

Kész! Most már tetszőleges számú pénzáramlást írhat be az A oszlopba, és a dinamikus belső megtérülési ráta képletei ennek megfelelően újraszámítódnak:

Az óvatlan felhasználók elleni óvintézkedésként, akik esetleg elfelejtik kitölteni az összes szükséges beviteli cellát, a hibák megelőzése érdekében a képleteket az IFERROR függvénybe csomagolhatja:

=IFERROR(IRR(Cash_flows), "")

=IFERROR(XIRR(Cash_flows, Dátumok), "")

=IFERROR(MIRR(Cash_flows, Finance_rate, Reinvest_rate), "")

Ne feledje, hogy ha a Finance_rate és/vagy Reinvest_rate cellák üresek, az Excel MIRR funkciója azt feltételezi, hogy ezek értéke nulla.

Hogyan készítsünk IRR-t Excelben a Goal Seek segítségével?

Az Excel IRR függvénye csak 20 iterációt hajt végre, hogy elérje az arányt, az XIRR pedig 100 iterációt hajt végre. Ha ennyi iteráció után nem találunk 0,00001%-on belül pontos eredményt, a rendszer #NUM! hibát küld vissza.

Ha nagyobb pontosságot szeretne elérni az IRR-számításhoz, akkor a What-If elemzés részét képező Goal Seek funkcióval több mint 32 000 iteráció elvégzésére kényszerítheti az Excelt.

Az ötlet az, hogy a Goal Seek találjon egy olyan százalékos rátát, amely az NPV-t 0-val teszi egyenlővé:

1. Állítsa be így a forrásadatokat:
   • Írja be a pénzáramlásokat egy oszlopba (ebben a példában B2:B7).
   • Tegye a várható IRR-t egy cellába (B9). Az érték, amit beír, tulajdonképpen nem számít, csak az NPV-képletet kell "táplálni" valamivel, ezért tegyen be bármilyen százalékos értéket, ami eszébe jut, mondjuk 10%-ot.
   • Írja be a következő NPV képletet egy másik cellába (B10):

=NPV(B9,B3:B7)+B2

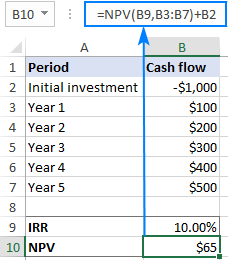
• Beállított cella - az NPV-cellára való hivatkozás (B10).
• Értékelni - írja be a 0-t, ami a kívánt érték a Set cellában.
• A sejtek megváltoztatásával - az IRR-cellára való hivatkozás (B9).

Ha kész, kattintson a OK .

Hasonló módon használhatja a Goal Seek funkciót az XIRR kiszámításához. Az egyetlen különbség az, hogy az NPV helyett az XNPV képletet kell használnia.

Megjegyzés: A Goal Seek segítségével megállapított IRR-érték a következő statikus , nem számítja újra dinamikusan, mint a képletek. Az eredeti adatok minden egyes változása után meg kell ismételnie a fenti lépéseket, hogy új IRR-t kapjon.

Így kell elvégezni az IRR-számítást Excelben. Ha közelebbről meg szeretné nézni a bemutatóban tárgyalt képleteket, akkor szívesen letölti az alábbi minta munkafüzetünket. Köszönöm, hogy elolvasta, és remélem, hogy jövő héten találkozunk a blogunkon!

Gyakorlati munkafüzet letölthető

Excel IRR kalkulátor - példák (.xlsx fájl)