Le tutoriel explique la formule des intérêts composés pour Excel et fournit des exemples de calcul de la valeur future de l'investissement à un taux d'intérêt composé annuel, mensuel ou quotidien. Vous trouverez également les étapes détaillées pour créer votre propre formule E Calculatrice d'intérêts composés xcel.

Les intérêts composés sont l'un des éléments de base de la banque et l'une des forces financières les plus puissantes qui déterminent le résultat de vos investissements.

Si vous n'êtes pas diplômé en comptabilité, analyste financier ou investisseur expérimenté, il peut être un peu difficile de saisir le concept à partir de livres et de manuels financiers spécialisés. L'objectif de cet article est de vous faciliter la tâche : ) Vous apprendrez également à utiliser une formule d'intérêts composés dans Excel et à créer une calculatrice d'intérêts composés universelle pour vos propres feuilles de calcul.

Qu'est-ce que l'intérêt composé ?

En termes très simples, les intérêts composés sont les intérêts gagnés sur les intérêts. Plus précisément, les intérêts composés sont gagnés à la fois sur le dépôt initial (principal) et sur les intérêts accumulés au cours des périodes précédentes.

Il est peut-être plus facile de commencer par l'intérêt simple qui n'est calculé que sur le montant principal. Par exemple, vous placez 10 $ sur un compte bancaire. Combien vaudra votre dépôt après un an à un taux d'intérêt annuel de 7 % ? La réponse est 10,70 $ (10 + 10*0,07 = 10,70), et votre intérêt gagné est de 0,70 $.

En cas de intérêt composé La banque ne vous rendra pas les intérêts perçus, mais les ajoutera à votre investissement principal. Ce montant accru devient le principal pour la période suivante (période de composition) et rapporte également des intérêts. En d'autres termes, vous gagnez des intérêts non seulement sur le montant principal, mais aussi sur les intérêts perçus dans chaque période de composition.

Dans notre exemple, en plus du montant principal de 10 $, les intérêts gagnés de 0,70 $ rapporteront également des intérêts l'année prochaine. Ainsi, combien vaudra votre dépôt de 10 $ après 2 ans au taux d'intérêt annuel de 7 % composé annuellement ? La réponse est 11,45 $ (10,7 + 10,7*0,07 = 11,45) et votre dépôt de 10 $ est de 10,7 $. intérêt gagné Comme vous le voyez, à la fin de la deuxième année, non seulement vous avez gagné 0,70 $ sur le dépôt initial de 10 $, mais vous avez également gagné 0,05 $ sur les 0,70 $ d'intérêts accumulés la première année.

Il existe plusieurs façons de calculer les intérêts composés dans Excel, et nous allons examiner chacune d'entre elles en détail.

Comment calculer les intérêts composés dans Excel

Les investissements à long terme peuvent être une stratégie efficace pour augmenter votre richesse, et même de petits dépôts peuvent faire une grande différence au fil du temps. Les formules Excel d'intérêts composés expliquées plus loin vous aideront à faire fonctionner la stratégie d'épargne. À terme, nous allons créer une formule universelle qui calcule la valeur future avec différentes périodes de composition - quotidienne, hebdomadaire, mensuelle, trimestrielle ouannuel.

Calcul des intérêts composés annuels dans Excel

Pour mieux comprendre l'idée des intérêts composés, commençons par un exemple très simple présenté au début de ce tutoriel et écrivons une formule pour calculer les intérêts composés annuels dans Excel. Comme vous vous en souvenez, vous investissez 10 $ au taux d'intérêt annuel de 7 % et vous voulez savoir comment les intérêts composés annuels augmentent votre épargne.

Intérêts composés annuels - formule 1

Une façon simple et directe de calculer le montant gagné avec un intérêt composé annuel est d'utiliser la formule pour augmenter un nombre par un pourcentage :

=Montant * (1 + %) .

Dans notre exemple, la formule est la suivante :

=A2*(1+$B2)

Où A2 est votre dépôt initial et B2 est le taux d'intérêt annuel. Veuillez noter que nous fixons la référence à la colonne B en utilisant le signe $.

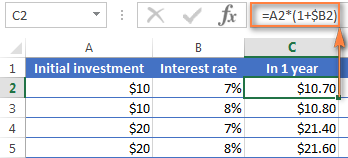
Comme vous vous en souvenez, 1% est une partie de cent, c'est-à-dire 0,01, donc 7% est 0,07, et c'est ainsi que les pourcentages sont réellement stockés dans Excel. En gardant cela à l'esprit, vous pouvez vérifier le résultat renvoyé par la formule en effectuant un simple calcul de 10*(1+0,07) ou 10*1,07 et vous assurer que votre solde après 1 an sera bien de 10,70 $.

Et maintenant, calculons le solde après 2 ans. Combien vaudra votre dépôt de 10 $ dans deux ans à un taux d'intérêt annuel de 7 % ? La réponse est 11,45 $ et vous pouvez l'obtenir en copiant la même formule dans la colonne D.

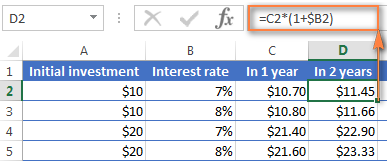
Pour calculer combien d'argent vous trouverez sur votre compte bancaire au bout de 3 ans, il suffit de copier la même formule dans la colonne E et vous obtiendrez 12,25 $.

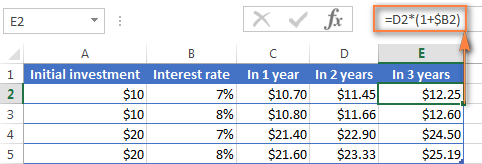
Ceux d'entre vous qui ont une certaine expérience des formules Excel ont probablement compris que la formule ci-dessus consiste en fait à multiplier trois fois le dépôt initial de 10 $ par 1,07 :

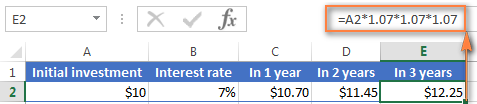
=10*1.07*1.07*1.07=12.25043

Arrondissez-le à deux décimales et vous obtiendrez le même chiffre que dans la cellule E2 de la capture d'écran ci-dessus - 12,25 $. Naturellement, vous pouvez calculer directement le solde après 3 ans en utilisant cette formule :

=A2*1.07*1.07*1.07

Intérêts composés annuels - formule 2

Une autre façon d'établir une formule d'intérêts composés annuels consiste à calculer les intérêts acquis pour chaque année, puis à les ajouter au dépôt initial.

En supposant que votre Dépôt initial est dans la cellule B1 et Taux d'intérêt annuel dans la cellule B2, la formule suivante fonctionne à merveille :

=B1 + B1 * $B$2

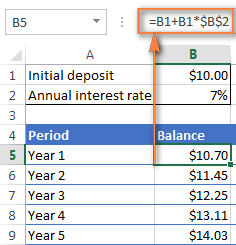
Pour que la formule fonctionne correctement, veuillez tenir compte des détails suivants :

• Corriger la référence à la Taux d'intérêt annuel (B2 dans notre cas) en ajoutant le signe $, il devrait s'agir d'une colonne absolue et d'une ligne absolue, comme $B$2.
• Pour l'année 2 (B6) et toutes les années suivantes, changez la formule en :

  Solde de l'année 1 + Solde de l'année 1 * Taux d'intérêt

Dans cet exemple, vous saisissez la formule suivante dans la cellule B6, puis vous la copiez sur d'autres lignes, comme le montre la capture d'écran ci-dessous :

=B5 + B5 * $B$2

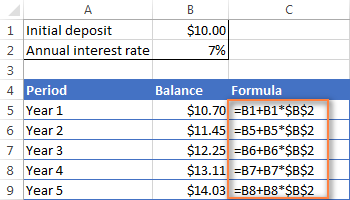
Pour connaître le montant des intérêts que vous avez réellement gagnés avec la capitalisation annuelle, soustrayez les Dépôt initial (B1) de Solde après 1 an (B5). Cette formule va à C5 :

=B5-B1

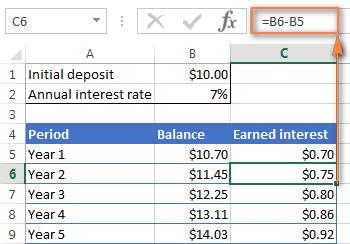
En C6, soustrayez Solde après 1 an de Solde après 2 ans et faites glisser la formule vers d'autres cellules :

=B6-B5

Vous devriez voir le intérêt gagné croissance comme dans la capture d'écran ci-dessous.

Les exemples ci-dessus illustrent bien l'idée des intérêts composés, n'est-ce pas ? Mais aucune des formules n'est assez bonne pour être qualifiée de formule universelle d'intérêts composés pour Excel. Tout d'abord, parce qu'elles ne vous permettent pas de spécifier une fréquence de composition, et ensuite, parce que vous devez construire un tableau entier plutôt que de simplement saisir une certaine durée et un certain taux d'intérêt.

Eh bien, faisons un pas en avant et créons une formule universelle d'intérêts composés pour Excel qui peut calculer combien d'argent vous gagnerez avec des intérêts composés annuels, trimestriels, mensuels, hebdomadaires ou quotidiens.

Formule générale d'intérêt composé

Lorsque les conseillers financiers analysent l'impact des intérêts composés sur un investissement, ils tiennent généralement compte de trois facteurs qui déterminent la valeur future de l'investissement (VF) :

• PV - valeur actuelle de l'investissement
• i - taux d'intérêt gagné au cours de chaque période
• n - nombre de périodes

En connaissant ces composants, vous pouvez utiliser la formule suivante pour obtenir le valeur future de l'investissement avec un certain taux d'intérêt composé :

Pour mieux illustrer le propos, voici quelques exemples rapides.

Exemple 1 : formule d'intérêt composé mensuel

Supposons que vous investissiez 2 000 $ à un taux d'intérêt de 8 % composé mensuellement et que vous vouliez connaître la valeur de votre investissement après 5 ans.

Tout d'abord, dressons une liste des composants de votre formule d'intérêts composés :

• PV = 2 000
• i = 8% par an, composé mensuellement (0,08/12= 006666667)
• n = 5 ans x 12 mois (5*12=60)

Entrez les chiffres ci-dessus dans la formule, et vous obtiendrez :

= $2,000 * (1 + 0.8/12)5x12

ou

= $2,000 * 1.00666666760

ou

= $2,000 * 1.489845708 = $2,979.69

Exemple 2 : formule d'intérêt composé quotidien

J'espère que l'exemple des intérêts composés mensuels est bien compris. Vous pouvez maintenant utiliser la même approche pour les intérêts composés quotidiens. L'investissement initial, le taux d'intérêt, la durée et la formule sont exactement les mêmes que dans l'exemple ci-dessus, seule la période de composition est différente :

• PV = 2 000
• i = 8% par an, composé quotidiennement (0,08/365 = 0,000219178)
• n = 5 ans x 365 jours (5*365 =1825)

Introduisez les chiffres ci-dessus dans la formule des intérêts composés, et vous obtiendrez le résultat suivant :

=$2,000 * (1 + 0.000219178)1825 = $2,983.52

Comme vous pouvez le constater, avec la capitalisation quotidienne, la valeur future du même investissement est un peu plus élevée qu'avec la capitalisation mensuelle, car le taux d'intérêt de 8 % ajoute des intérêts au montant principal chaque jour plutôt que chaque mois. Comme vous pouvez le deviner, le résultat de la capitalisation mensuelle sera plus élevé que celui de la capitalisation annuelle.

Tout cela est bien, mais ce que vous voulez vraiment, c'est une formule Excel pour les intérêts composés, n'est-ce pas ? Restez avec moi un peu plus longtemps, s'il vous plaît. Nous arrivons maintenant à la partie la plus intéressante : construire votre propre calculateur d'intérêts composés puissant et polyvalent dans Excel.

Formule de calcul des intérêts composés dans Excel (composition quotidienne, hebdomadaire, mensuelle, annuelle)

En général, il y a plus d'une façon de faire quelque chose dans Excel et une formule d'intérêts composés ne fait pas exception :) Bien que Microsoft Excel ne fournisse aucune fonction spéciale pour le calcul des intérêts composés, vous pouvez utiliser d'autres fonctions pour créer votre propre calculateur d'intérêts composés.

Commençons par créer notre calculatrice Excel d'intérêts composés en saisissant les facteurs de base qui déterminent la valeur future d'un investissement dans une feuille de calcul Excel :

• investissement initial (B3)
• taux d'intérêt annuel (B4)
• nombre de périodes de composition par an (B5)
• nombre d'années (B6)

Une fois terminé, votre feuille Excel peut ressembler à ceci :

Tout ce dont vous avez besoin maintenant, c'est de la formule d'intérêts composés pour calculer le montant gagné (solde) en fonction des valeurs saisies. La bonne nouvelle, c'est que vous n'avez pas à réinventer la roue. Nous allons simplement prendre la formule d'intérêts composés éprouvée utilisée par les banques et autres institutions financières et la traduire dans le langage d'Excel.

Formule de calcul des intérêts composés pour Excel :

Pour les données sources ci-dessus, la formule prend cette forme :

=B3 * (1 + B4 /B5) ^ (B6 * B5)

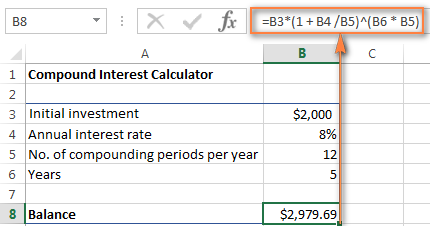
Les chiffres vous semblent familiers ? Oui, ce sont les mêmes valeurs et calculs que nous avons effectués avec une formule d'intérêts composés mensuels, et le résultat prouve que nous avons tout bien fait !

Si vous voulez savoir combien vaudra votre investissement à un taux d'intérêt annuel de 8% composé trimestrielle il suffit d'entrer 4 dans la cellule B5 :

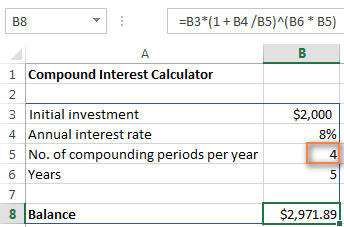
Pour calculer la valeur future de votre investissement avec semestriel composé, entrez 2 comme Périodes de capitalisation par an valeur. Pour hebdomadaire taux d'intérêt, entrez 52, c'est le nombre de semaines que contient chaque année. Si vous vous intéressez à quotidien composer, entrer 365, et ainsi de suite.

Pour trouver la quantité de intérêt gagné Dans ce cas, il suffit de calculer la différence entre la valeur future (solde) et la valeur actuelle (investissement initial). Dans notre cas, la formule de B9 est aussi simple que cela :

=B8-B3

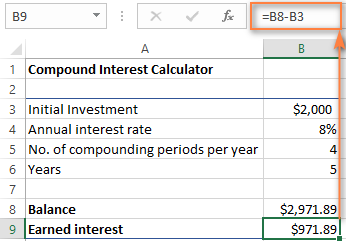
Comme vous le voyez, nous avons créé une calculatrice d'intérêts composés vraiment universelle pour Excel. J'espère que vous n'aurez pas à regretter d'avoir investi quelques précieuses minutes pour comprendre la délicate formule d'intérêts composés utilisée par les planificateurs financiers : ).

Calculateur avancé d'intérêts composés pour Excel

Si, pour une raison quelconque, l'approche ci-dessus ne vous convient pas, vous pouvez créer votre calculatrice d'intérêts composés Excel à l'aide de la fonction FV disponible dans toutes les versions d'Excel 2000 à 2019.

La fonction FV calcule la valeur future d'un investissement sur la base de données d'entrée similaires à celles que nous avons examinées, bien que sa syntaxe soit un peu différente :

L'explication détaillée des arguments peut être trouvée dans le tutoriel sur la fonction FV d'Excel.

En attendant, construisons une formule de VF en utilisant les mêmes données sources que dans l'exemple des intérêts composés mensuels et voyons si nous obtenons le même résultat.

Comme vous vous en souvenez peut-être, nous avons déposé 2 000 $ pendant 5 ans sur un compte d'épargne à un taux d'intérêt annuel de 8 % composé mensuellement, sans paiement supplémentaire. Notre formule d'intérêt composé est donc la suivante :

=FV(0.08/12, 5*12, ,-2000)

Si vous avez besoin d'une explication des paramètres, la voici :

• Le taux est de 0,008/12 puisque vous avez le taux d'intérêt annuel de 8% composé mensuellement.
• nper est 5*12, c'est-à-dire 5 ans * 12 mois
• pmt est laissé vide car nous n'avons pas de paiements supplémentaires.
• pv est de -2000 puisqu'il s'agit d'une sortie et qu'elle doit être représentée par un nombre négatif.

Saisissez la formule ci-dessus dans une cellule vide, et le résultat sera de 2 979,69 $ (ce qui correspond parfaitement au résultat du calcul mathématique effectué dans l'exemple des intérêts composés mensuels).

Naturellement, rien ne vous empêche de remplacer les valeurs par des références de cellules :

=FV(B4/B5, B6*B5, , -B3)

La capture d'écran ci-dessous montre la valeur future d'un investissement de 4 000 $ après 15 ans à un taux d'intérêt annuel de 7 % composé hebdomadairement :

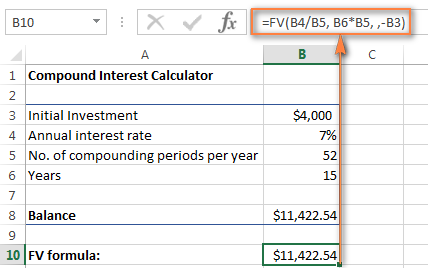
Pour rendre votre calculatrice d'intérêts composés Excel encore plus puissante, vous pouvez l'étendre avec la fonction Contributions supplémentaires (paiements supplémentaires) et modifiez la formule des intérêts composés en conséquence.

=FV(B4/B5, B6*B5, -B8, -B3, B9)

Où :

• B3 - investissement principal
• B4 - taux d'intérêt annuel
• B5 - le nombre de périodes de composition par an
• B6 - le nombre d'années à épargner
• B8 - contributions supplémentaires (facultatif)
• B9 - type de cotisations supplémentaires. N'oubliez pas que vous entrez 1 si vous déposez un montant supplémentaire au début de la période de capitalisation, 0 ou omis si les paiements supplémentaires sont effectués à la fin de la période.

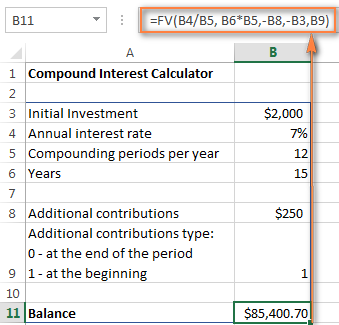
Si vous êtes curieux d'essayer cette calculatrice avancée d'intérêts composés pour Excel pour calculer vos économies, vous pouvez la télécharger à la fin de cet article.

Conseil : une autre façon rapide de calculer les intérêts composés consiste à effectuer une analyse d'hypothèses à l'aide d'un tableau de données Excel.

Calculateurs d'intérêts composés en ligne

Si vous préférez investir de l'argent plutôt que du temps pour savoir comment calculer les intérêts composés dans Excel, les calculatrices d'intérêts composés en ligne peuvent vous être utiles. Vous pouvez en trouver un grand nombre en entrant quelque chose comme "calculatrice d'intérêts composés" dans votre moteur de recherche préféré. En attendant, laissez-moi vous présenter rapidement quelques-unes de mes préférées.

Calculateur d'intérêts composés par Bankrate

Les principaux avantages de la calculatrice d'intérêts composés de Bankrate sont la facilité d'utilisation et la présentation visuelle des résultats. Cette calculatrice vous permet d'entrer les données d'épargne manuellement dans des cases ou en déplaçant un curseur. Au fur et à mesure, le total estimé s'affiche en haut et se reflète immédiatement dans le graphique ci-dessous :

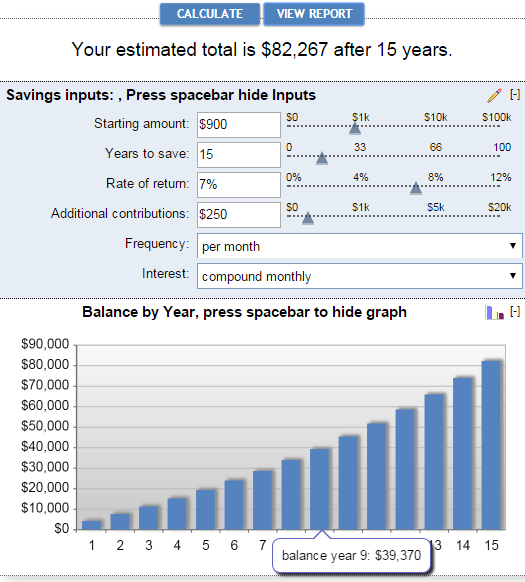
En cliquant sur le Voir le rapport génère un "Rapport de synthèse" ainsi qu'un "Solde d'épargne" qui fournit des informations détaillées sur le montant des cotisations supplémentaires, les intérêts acquis et le solde pour chaque année.

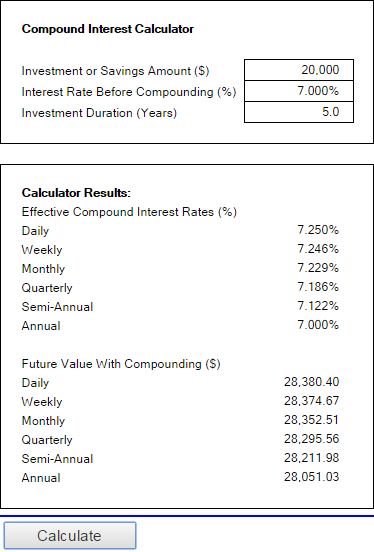
Calculateur d'intérêts composés par Money-Zine

La calculatrice en ligne de Money-Zine est beaucoup plus simple que celle de Bankrate. Elle ne vous demande de spécifier que trois valeurs : le montant de l'investissement, le taux d'intérêt et la durée. Dès que vous avez fourni ces chiffres et que vous avez cliqué sur le bouton Calculer il vous montrera tous les types de taux d'intérêt composés (quotidien, hebdomadaire, mensuel, annuel, etc.) ainsi que les valeurs futures avec une composition correspondante.

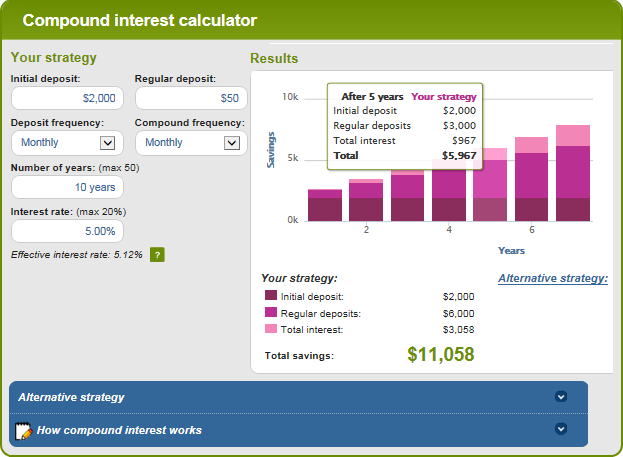
Calculateur d'intérêts composés par MoneySmart

Il s'agit d'une très belle calculatrice d'intérêts composés en ligne, gérée par l'Australian Securities and Investments Commission. Elle vous permet de saisir tous les facteurs pertinents qui déterminent la valeur future de votre investissement et affiche le résultat sous forme de graphique. En survolant une certaine barre du graphique, vous pouvez voir les informations récapitulatives pour cette année particulière.

Voilà comment calculer les intérêts composés dans Excel et en dehors :) J'espère qu'au moins une formule d'intérêts composés abordée dans cet article vous aura été utile. Quoi qu'il en soit, je vous remercie de votre lecture et j'espère vous voir sur notre blog la semaine prochaine !

Cahier d'exercices à télécharger

Calculateur d'intérêts composés pour Excel (fichier .xlsx)