නිබන්ධනය Excel සඳහා සංයුක්ත පොලී සූත්‍රය පැහැදිලි කරන අතර ආයෝජනයේ අනාගත වටිනාකම වාර්ෂික, මාසික හෝ දෛනික සංයුක්ත පොලී අනුපාතයට ගණනය කරන්නේ කෙසේද යන්න පිළිබඳ උදාහරණ සපයයි. ඔබේම E xcel සංයුක්ත පොලී කැල්කියුලේටරය සෑදීමේ සවිස්තරාත්මක පියවරයන් ද ඔබ සොයා ගනු ඇත.

සංයුක්ත පොලී යනු බැංකුකරණයේ මූලික ගොඩනැඟිලි කොටස්වලින් එකක් වන අතර වඩාත්ම බලගතු මූල්‍ය ක්‍රමයකි. ඔබේ ආයෝජනවල ප්‍රතිඵලය තීරණය කරන්නේ එය වටා ඇති බලවේගය.

ඔබ ගිණුම්කරණ උපාධිධාරියෙක්, මුල්‍ය විශ්ලේෂකයෙක් හෝ පළපුරුදු ආයෝජකයෙක් නම් මිස, විශේෂිත මූල්‍ය පොත් සහ අත්පොත් වලින් සංකල්පය ග්‍රහණය කර ගැනීම තරමක් අපහසු විය හැක. මෙම ලිපියේ අරමුණ එය පහසු කරවීමයි : ) ඔබ Excel හි සංයුක්ත පොලී සූත්‍රයක් භාවිතා කරන ආකාරය සහ ඔබේම වැඩ පත්‍රිකා සඳහා විශ්වීය සංයුක්ත පොලී කැල්කියුලේටරයක් ​​නිර්මාණය කරන්නේ කෙසේදැයි ඉගෙන ගනු ඇත.

කුමක්ද? සංයුක්ත පොලී ද?

ඉතා සරල වචන වලින්, සංයුක්ත පොලී යනු පොලී මත උපයන පොලියයි. වඩාත් නිවැරදිව, මුලික තැන්පතුව (ප්‍රධාන) සහ පෙර කාල පරිච්ඡේද වලින් එකතු වූ පොලිය යන දෙකටම සංයුක්ත පොලී උපයනු ලැබේ.

සමහර විට, මූලික මුදල මත පමණක් ගණනය කරන සරල පොලියකින් ආරම්භ කිරීම පහසු විය හැක. උදාහරණයක් ලෙස, ඔබ බැංකු ගිණුමකට ඩොලර් 10 ක් දමා ඇත. 7% ක වාර්ෂික පොලී අනුපාතයකට වසරකට පසු ඔබේ තැන්පතුව කොපමණ වටිනවාද? පිළිතුර $10.70 (10 + 10*0.07 =සංයුක්ත පොලී සූත්‍රය පහත පරිදි වේ:

=FV(0.08/12, 5*12, ,-2000)

ඔබට පරාමිති පිළිබඳ යම් පැහැදිලි කිරීමක් අවශ්‍ය නම්, මෙතැනින් යන්න:

• අනුපාතය 0.008/12 වේ 8% වාර්ෂික පොලී අනුපාතය මාසිකව සංයුක්ත වේ.
• nper 5*12, එනම් වසර 5 * මාස 12
• pmt හිස්ව තබන්නේ අපට අමතර ගෙවීම් නොමැති බැවිනි.
• pv යනු -2000 වන අතර එය පිටතට ගලා යාමක් වන අතර එය සෘණ අංකයකින් නිරූපණය කළ යුතුය.

ඉහත සූත්‍රය හිස් කොටුවක ඇතුළු කරන්න, ප්‍රතිඵලය ලෙස එය $2,979.69 ප්‍රතිදානය කරයි (එය ප්‍රතිඵලයක් ලෙස සම්පුර්ණයෙන්ම අනුගත වේ. මාසික සංයුක්ත පොලී උදාහරණයේ සිදු කරන ලද ගණිත ගණනය කිරීමේ ප්‍රතිඵලය).

ස්වාභාවිකව, සෛල යොමු සමඟ අගයන් ප්‍රතිස්ථාපනය කිරීමෙන් කිසිවක් ඔබව වළක්වන්නේ නැත:

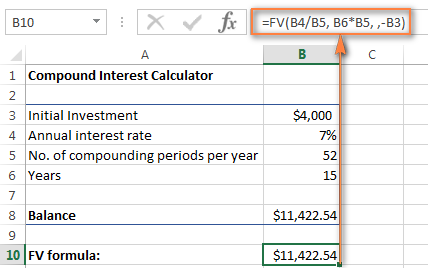
=FV(B4/B5, B6*B5, , -B3)

පහත තිර රුව පෙන්වයි වසර 15කට පසු ඩොලර් 4,000ක ආයෝජනයේ අනාගත වටිනාකම සතිපතා 7%ක වාර්ෂික පොලී අනුපාතයක් සමඟ සංයුක්ත වේ:

ඔබේ Excel සංයුක්ත පොලී කැල්කියුලේටරය වඩාත් බලවත් කිරීමට, ඔබට එය දීර්ඝ කළ හැක අමතර දායකත්ව විකල්පය සමඟ n (අමතර ගෙවීම්) සහ ඒ අනුව සංයුක්ත පොලී සූත්‍රය වෙනස් කරන්න.

=FV(B4/B5, B6*B5, -B8, -B3, B9)

කොහේ:

• B3 - ප්‍රධාන ආයෝජනය
• B4 - වාර්ෂික පොලී අනුපාතිකය
• B5 - වසරකට සංයෝජන කාල ගණන
• B6 - ඉතිරි කිරීමට වසර ගණන
• B8 - අමතර දායක මුදල් (විකල්ප)
• B9 - අතිරේක දායකත්ව වර්ගය. ඔබ තැන්පත් කරන්නේ නම් 1 ඇතුලත් කරන බව මතක තබා ගන්නසංයෝජන කාලය ආරම්භයේදී අමතර මුදල, 0 හෝ කාලසීමාව අවසානයේ අමතර ගෙවීම් සිදු කරන්නේ නම් එය මග හැරේ ඔබගේ ඉතුරුම් ගණනය කිරීම සඳහා Excel සඳහා උසස් සංයුක්ත පොලී කැල්ක්යුලේටරය, ඔබට මෙම සටහන අවසානයේ එය බාගත කළ හැක.

  ඉඟිය. සංයුක්ත පොලී ගණනය කිරීමට තවත් ඉක්මන් ක්‍රමයක් නම් Excel දත්ත වගුවේ ආධාරයෙන් What-If විශ්ලේෂණය කිරීමයි.

  සාමූහික පොලී ගණක යන්ත්‍ර ඔන්ලයින්

  ඔබ කැමති නම් මුදල් ආයෝජනය කරන්නේ කෙසේද යන්න සොයා බැලීමේදී එක්සෙල් හි සංයුක්ත පොලී ගණනය කිරීම සඳහා, සබැඳි සංයුක්ත පොලී ගණක යන්ත්‍ර ප්‍රයෝජනවත් විය හැක. ඔබ කැමති සෙවුම් යන්ත්‍රය තුළ "සංයුක්ත පොලී කැල්කියුලේටරය" වැනි යමක් ඇතුළත් කිරීමෙන් ඔබට ඒවා ඕනෑ තරම් සොයා ගත හැක. මේ අතරතුර, මගේ ප්‍රියතම ඒවා කිහිපයක් ඉක්මනින් ඉදිරිපත් කිරීමට මට ඉඩ දෙන්න.

  Bankrate මගින් සංයුක්ත පොලී කැල්කියුලේටරය

  Bankrate සංයෝග පොලී කැල්කියුලේටරයේ ප්‍රධාන ප්‍රතිලාභ වන්නේ භාවිතයේ පහසුව සහ දෘශ්‍ය ඉදිරිපත් කිරීමයි. ප්රතිඵල. මෙම කැල්කියුලේටරය ඔබට පෙට්ටිවල හෝ ස්ලයිඩරයක් ගෙනයාමෙන් ඉතුරුම් යෙදවුම් හස්තීයව ඇතුළු කිරීමට ඉඩ සලසයි. ඔබ මෙය කරන විට, ඇස්තමේන්තුගත එකතුව ඉහළින් දර්ශනය වන අතර වහාම පහත ප්‍රස්ථාරයෙන් පිළිබිඹු වේ:

  

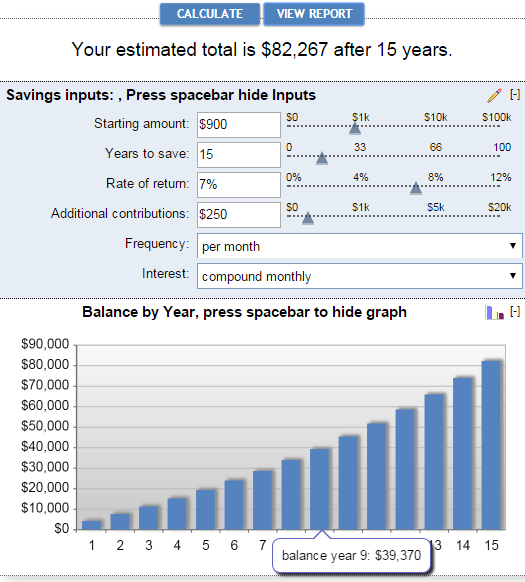
  වාර්තාව බලන්න බොත්තම ක්ලික් කිරීමෙන් "සාරාංශයක් ජනනය වේ. අතිරේක දායකත්ව ප්‍රමාණය, උපයාගත් පොලී සහ ශේෂය පිළිබඳ සවිස්තරාත්මක තොරතුරු සපයන "ඉතුරුම් ශේෂය" වාර්තාව"එක් එක් වසර සඳහා.

  Money-Zine විසින් සංයුක්ත පොලී කැල්කියුලේටරය

  Money-Zine වෙතින් වන මාර්ගගත ගණක යන්ත්‍රය Bankrate ගේ එක හා සසඳන විට ඉතා සරල ය. අගයන් 3ක් පමණක් සඳහන් කිරීමට එය ඔබෙන් අසයි: ප්‍රධාන ආයෝජනය, පොලී අනුපාතය සහ කාලසීමාව. ඔබ මෙම අංක සපයා ගණනය කරන්න බොත්තම ක්ලික් කළ වහාම, එය ඔබට සියලු වර්ගවල සංයුක්ත පොලී අනුපාත (දිනපතා, සතිපතා, මාසික, වාර්ෂික, ආදිය) මෙන්ම අනාගත අගයන් ද පෙන්වනු ඇත. Compounding.

  

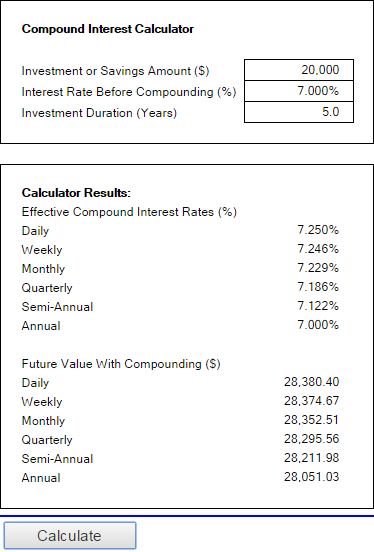
  MoneySmart විසින් සංයුක්ත පොලී කැල්කියුලේටරය

  මෙය ඕස්ට්‍රේලියානු සුරැකුම්පත් සහ ආයෝජන කොමිෂන් සභාව විසින් පවත්වාගෙන යනු ලබන ඉතා හොඳ සබැඳි සංයුක්ත පොලී ගණක යන්ත්‍රයකි. එය ඔබගේ ආයෝජනයේ අනාගත වටිනාකම තීරණය කරන සහ ප්‍රස්ථාරයක් ලෙස ප්‍රතිදානය කරන සියලුම අදාළ සාධක ඇතුළත් කිරීමට ඔබට ඉඩ සලසයි. ප්‍රස්ථාරයේ යම් තීරුවක් මත සැරිසැරීමෙන්, ඔබට එම වර්ෂය සඳහා සාරාංශ තොරතුරු දැකිය හැකිය.

  

  බලන්න: Excel සැකිලි: සාදන ආකාරය සහ භාවිතා කරන ආකාරය

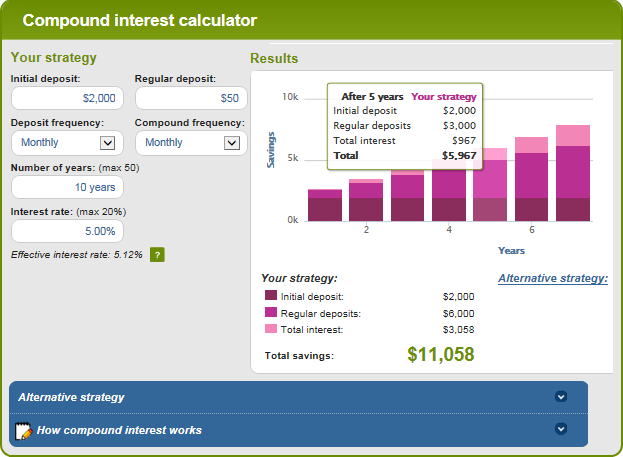
  ඔබ Excel සහ ඉන් පිටත සංයුක්ත පොලී ගණනය කරන්නේ මෙලෙසයි :) මෙම ලිපියේ සාකච්ඡා කර ඇති අවම වශයෙන් එක් සංකීර්ණ පොලී සූත්‍රයක් ඔබට ප්‍රයෝජනවත් වී ඇතැයි මම බලාපොරොත්තු වෙමි. කෙසේ වෙතත්, කියවීම ගැන මම ඔබට ස්තූතිවන්ත වන අතර ලබන සතියේ අපගේ බ්ලොග් අඩවියෙන් ඔබව දැකීමට බලාපොරොත්තු වෙමි!

  බාගැනීම සඳහා වැඩපොත පුහුණු වන්න

  Excel (.xlsx ගොනුව) සඳහා සංයුක්ත පොලී කැල්කියුලේටරය

  10.70), සහ ඔබේ උපයා ඇති පොළිය $0.70 වේ.

  සාමූහික පොළිය නම්, එක් එක් කාල සීමාව තුළ ප්‍රධාන වෙනස් වේ. බැංකුව උපයාගත් පොලිය ඔබට ආපසු ලබා නොදෙනු ඇත, ඒ වෙනුවට ඔවුන් එය ඔබේ මූලික ආයෝජනයට එකතු කරයි. මෙම වැඩි කරන ලද මුදල ඊළඟ කාල සීමාව සඳහා (සංයුක්ත කාලය) මූලික බවට පත් වන අතර පොලී ද උපයා ගනී. වෙනත් වචන වලින් කිවහොත්, ඔබ මූලික මුදල මත පමණක් නොව, එක් එක් සංයෝග කාල සීමාව තුළ උපයන පොලිය මතද පොලී උපයනු ඇත.

  අපගේ උදාහරණයේ දී, $10 හි මූලික මුදලට අමතරව, උපයාගත් $0.70 ක පොලිය වනු ඇත. ලබන වසරේ පොලී උපයන්න. ඉතින්, ඔබේ ඩොලර් 10 තැන්පතුව වසර 2 කට පසු වාර්ෂිකව 7% ක වාර්ෂික පොලී අනුපාතයට කොපමණ වටිනවාද? පිළිතුර $11.45 (10.7 + 10.7*0.07 = 11.45) වන අතර ඔබේ උපයා ඇති පොලිය $1.45 වේ. ඔබට පෙනෙන පරිදි, දෙවන වසර අවසානයේදී, ඔබ ආරම්භක $10 තැන්පතුවෙන් $0.70ක් උපයා ගත්තා පමණක් නොව, පළමු වසර තුළ එකතු වූ $0.70 පොලියෙන් $0.05ක් ද උපයා ඇත.

  Excel හි සංයුක්ත පොලී ගණනය කිරීමට ක්‍රම කිහිපයක් ඇති අතර, අපි ඒ සෑම එකක්ම විස්තරාත්මකව සාකච්ඡා කරන්නෙමු.

  Excel හි සංයුක්ත පොලී ගණනය කරන්නේ කෙසේද

  දිගුකාලීන ආයෝජන ඔබේ ධනය වැඩි කිරීමට ඵලදායී උපාය මාර්ගයක් විය හැකි අතර, කුඩා තැන්පතු පවා කාලයත් සමඟ විශාල වෙනසක් ඇති කළ හැකිය. තවදුරටත් විස්තර කර ඇති Excel සංයුක්ත පොලී සූත්‍ර ඔබට ඉතුරුම් උපාය මාර්ගය ලබා ගැනීමට උපකාරී වනු ඇතකාර්යය. අවසානයේදී, අපි දිනපතා, සතිපතා, මාසිකව, කාර්තුමය හෝ වාර්ෂිකව විවිධ සංයෝග කාල පරිච්ඡේද සමඟින් අනාගත අගය ගණනය කරන විශ්වීය සූත්‍රයක් සෑදීමට යන්නෙමු.

  Excel හි වාර්ෂික සංයුක්ත පොලී ගණනය කිරීම

  ට සංයුක්ත පොලී පිළිබඳ අදහස වඩා හොඳින් තේරුම් ගන්න, මෙම නිබන්ධනය ආරම්භයේ සාකච්ඡා කර ඇති ඉතා සරල උදාහරණයකින් ආරම්භ කර Excel හි වාර්ෂික සංයුක්ත පොලී ගණනය කිරීම සඳහා සූත්‍රයක් ලියන්න. ඔබට මතක ඇති පරිදි, ඔබ 7% ක වාර්ෂික පොලී අනුපාතයට ඩොලර් 10 ක් ආයෝජනය කරන අතර වාර්ෂික සංයෝග කිරීම ඔබේ ඉතුරුම් වැඩි කරන්නේ කෙසේදැයි දැන ගැනීමට අවශ්‍යයි.

  වාර්ෂික සංයුක්ත පොලී - සූත්‍රය 1

  පහසු සහ සරල ක්‍රමයක් වාර්ෂික සංයුක්ත පොලී සමඟ උපයාගත් මුදල ගණනය කිරීම සඳහා සංඛ්‍යාවක් ප්‍රතිශතයකින් වැඩි කිරීමට සූත්‍රය භාවිතා කරයි:

  =Amount * (1 + %) .

  අපගේ උදාහරණයේ, සූත්‍රය වන්නේ:

  =A2*(1+$B2)

  A2 ඔබේ මූලික තැන්පතුව වන අතර B2 යනු වාර්ෂික පොලී අනුපාතයයි. අපි $ ලකුණ භාවිතයෙන් B තීරුව වෙත යොමුව නිවැරදි කරන බව කරුණාවෙන් සලකන්න.

  

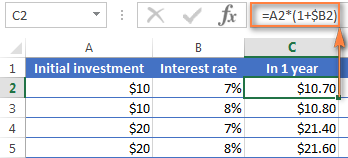
  ඔබට මතක ඇති පරිදි, 1% යනු සියයෙන් එක කොටසකි, එනම් 0.01, එබැවින් 7 % යනු 0.07 ක් වන අතර, Excel හි ප්‍රතිශත සැබවින්ම ගබඩා කර ඇත්තේ එලෙස ය. මෙය මතක තබා ගනිමින්, ඔබට 10*(1+0.07) හෝ 10*1.07 සරල ගණනය කිරීමක් සිදු කිරීමෙන් සූත්‍රය මඟින් ලබා දෙන ප්‍රතිඵලය සත්‍යාපනය කර වසර 1කට පසු ඔබේ ශේෂය ඇත්ත වශයෙන්ම $10.70 වනු ඇති බවට වග බලා ගන්න.

  හා දැන් අපි වසර 2කට පසු ඉතිරිය ගණනය කරමු. ඉතින් කොහොමද7% ක වාර්ෂික පොලී අනුපාතයකට වසර දෙකකින් ඔබේ ඩොලර් 10 තැන්පතු බොහෝමයක් වටිනවාද? පිළිතුර $11.45 වන අතර එම සූත්‍රයම D තීරුවට පිටපත් කිරීමෙන් ඔබට එය ලබාගත හැක.

  

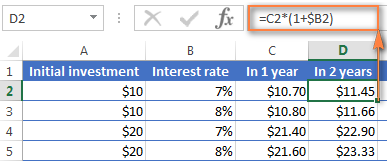
  3 අවසානයේ ඔබේ බැංකු ගිණුමේ කොපමණ මුදලක් සොයා ගත හැකිදැයි ගණනය කිරීමට වසර, එම සූත්‍රය E තීරුවට පිටපත් කරන්න, එවිට ඔබට $12.25 ලැබෙනු ඇත.

  

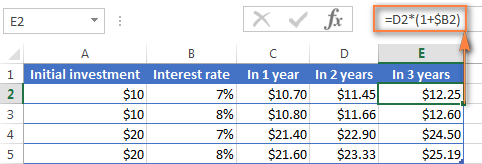
  එක්සෙල් සූත්‍ර පිළිබඳ යම් අත්දැකීමක් ඇති ඔබ ඉහත සූත්‍රය කුමක්දැයි වටහාගෙන ඇත. ඇත්ත වශයෙන්ම කරන්නේ $10 හි ආරම්භක තැන්පතුව 1.07 න් තුන් වරක් ගුණ කිරීමයි:

  =10*1.07*1.07*1.07=12.25043

  එය දශම ස්ථාන දෙකකට වට කරන්න, එවිට ඔබට ඉහත තිර පිටුවේ E2 කොටුවේ පෙනෙන අංකයම ලැබේ. - $12.25. ස්වාභාවිකවම, ඔබට මෙම සූත්‍රය භාවිතයෙන් වසර 3කට පසු ශේෂය කෙලින්ම ගණනය කළ හැක:

  =A2*1.07*1.07*1.07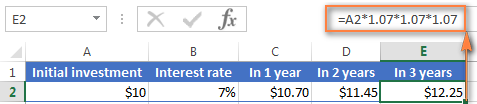

  

  වාර්ෂික සංයුක්ත පොලී - සූත්‍රය 2

  තවත් වාර්ෂික සංයුක්ත පොලී සූත්‍රයක් සෑදීමේ ක්‍රමය නම් එක් එක් වර්ෂය සඳහා උපයාගත් පොලිය ගණනය කර එය මූලික තැන්පතුවට එකතු කිරීමයි.

  ඔබේ මුල් තැන්පතුව B1 සහ <1 කොටුවේ ඇතැයි උපකල්පනය කිරීම>වාර්ෂික පොලී අනුපාතය B2 කොටුවේ, පහත සූත්‍රය සංග්‍රහයක් ලෙස ක්‍රියා කරයි:

  =B1 + B1 * $B$2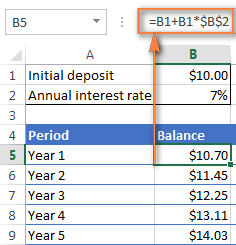

  

  සූත්‍රය නිවැරදිව ක්‍රියා කිරීමට, කරුණාකර මතක තබා ගන්න පහත විස්තර:

  • $ ලකුණ එකතු කිරීමෙන් වාර්ෂික පොලී අනුපාතය කොටුව (අපගේ නඩුවේ B2) වෙත යොමුව සවි කරන්න, එය නිරපේක්ෂ තීරුවක් සහ නිරපේක්ෂ පේළියක් විය යුතුය. $B$2.
  • 2 වසර සඳහා (B6)සහ සියලු පසු වසර, සූත්‍රය වෙනස් කරන්න:

    වසර 1 ශේෂය + වසර 1 ශේෂය * පොලී අනුපාතිකය

  මෙම උදාහරණයේදී, ඔබ පහත සූත්‍රය B6 කොටුවේ ඇතුළු කළ යුතු අතර ඉන්පසු පහත තිර රුවෙහි පෙන්වා ඇති පරිදි එය වෙනත් පේළිවලට පිටපත් කරන්න:

  =B5 + B5 * $B$2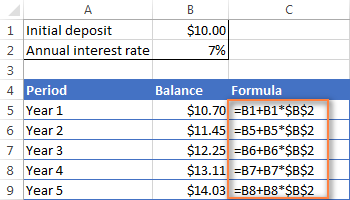

  

  වාර්ෂික සංයෝගය සමඟ ඔබ ඇත්ත වශයෙන්ම උපයාගත් පොලී ප්‍රමාණය සොයා ගැනීමට, ආරම්භක තැන්පතුව (B1) ශේෂයෙන් වසර 1 කට පසු (B5) අඩු කරන්න. මෙම සූත්‍රය C5 වෙත යයි:

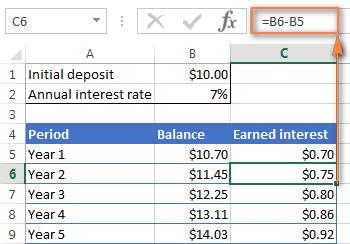
  =B5-B1

  C6 හි, වසර 1කට පසු ශේෂය වසර 2කට පසු ශේෂය වෙතින් අඩු කර, සූත්‍රය පහළට අදින්න. අනෙකුත් සෛල වෙත:

  =B6-B5

  පහත තිර රුවෙහි මෙන් ඔබ උපයා ඇති පොලී වර්ධනය දැකිය යුතුය.

  

  සංකීර්ණ පොලී පිළිබඳ අදහස නිදර්ශනය කිරීමට ඉහත උදාහරණ හොඳ කාර්යයක් කරනවා නේද? නමුත් එක්සෙල් සඳහා විශ්වීය සංයුක්ත පොලී සූත්‍රයක් ලෙස හැඳින්වීමට තරම් සූත්‍ර කිසිවක් හොඳ නැත. පළමුව, ඔවුන් ඔබට සංයෝග සංඛ්‍යාතයක් නියම කිරීමට ඉඩ නොදෙන නිසාත්, දෙවනුව, ඔබට නිශ්චිත කාල සීමාවක් සහ පොලී අනුපාතයක් ඇතුළත් කරනවාට වඩා සම්පූර්ණ වගුවක් තැනීමට ඇති නිසා.

  හොඳයි, අපි පියවරක් ඉදිරියට තබා නිර්මාණය කරමු. ඔබ වාර්ෂික, කාර්තුමය, මාසික, සතිපතා හෝ දෛනික සංයෝගය සමඟ කොපමණ මුදලක් උපයනු ඇත්දැයි ගණනය කළ හැකි Excel සඳහා විශ්වීය සංයුක්ත පොලී සූත්‍රයක්.

  සාමාන්‍ය සංයුක්ත පොලී සූත්‍රය

  මුල්‍ය උපදේශකයින් බලපෑම විශ්ලේෂණය කරන විට මත සංයුක්ත පොලීආයෝජනය, ඔවුන් සාමාන්‍යයෙන් ආයෝජනයේ අනාගත වටිනාකම තීරණය කරන සාධක තුනක් සලකා බලයි (FV):

  • PV - ආයෝජනයේ වර්තමාන වටිනාකම
  • i - එක් එක් කාල සීමාව තුළ උපයන පොලී අනුපාතය
  • n - කාලපරිච්ඡේද ගණන

  මෙම කොටස් දැනගැනීමෙන්, ඔබට පහත සූත්‍රය භාවිතා කර යම් සංයුක්ත පොලී අනුපාතයක් සමඟ ආයෝජනයේ අනාගත අගය ලබා ගත හැක. :

  FV = PV * (1 + i)n

  කාර්යය වඩාත් හොඳින් නිදර්ශනය කිරීම සඳහා, මෙන්න ඉක්මන් උදාහරණ කිහිපයක්.

  උදාහරණ 1: මාසික සංයුක්ත පොලී සූත්‍රය

  සිතන්න, ඔබ මාසිකව 8% පොලී අනුපාතයකින් ඩොලර් 2,000ක් ආයෝජනය කරන අතර ඔබට වසර 5කට පසු ඔබේ ආයෝජනයේ වටිනාකම දැන ගැනීමට අවශ්‍ය වේ.

  මුලින්ම, අපි ඔබේ සංයුක්ත පොලී සූත්‍රය සඳහා සංරචක ලැයිස්තුවක් ලියා ගනිමු:

  • PV = $2,000
  • i = වසරකට 8%, සංයුක්ත මාසික (0.08/12= 006666667)
  • n = අවුරුදු 5 x මාස 12 (5*12= 60)

  සූත්‍රයේ ඉහත සංඛ්‍යා ඇතුළත් කරන්න, එවිට ඔබට ලැබෙනු ඇත:

  = $2,000 * (1 + 0.8/12)5x12

  හෝ

  = $2,000 * 1.00666666760

  හෝ

  = $2,000 * 1.489845708 = $2,979.69

  උදාහරණ 2: දෛනික සංයුක්ත පොලී සූත්‍රය

  මාසික සංයෝග පොලී උදාහරණය හොඳින් අවබෝධ වී ඇතැයි මම බලාපොරොත්තු වෙමි, දැන් ඔබට දෛනික සංයෝග කිරීම සඳහා එම ප්‍රවේශයම භාවිත කළ හැකිය. මූලික ආයෝජනය, පොලී අනුපාතය, කාලසීමාව සහ සූත්‍රය ඉහත උදාහරණයේ හරියටම සමාන වේ, සංයෝග කාලය පමණක් වෙනස් වේ:

  • PV = $2,000
  • i = 8% වසරකට, දිනපතා සංයුක්ත(0.08/365 = 0.000219178)
  • n = අවුරුදු 5 x 365 දින (5*365 =1825)

  ඉහත අංක සංයුක්ත පොලී සූත්‍රයට සපයන්න, එවිට ඔබට ලැබෙනු ඇත පහත ප්‍රතිඵලය:

  =$2,000 * (1 + 0.000219178)1825 = $2,983.52

  ඔබ දකින පරිදි, දෛනික සංයුක්ත පොලී සමඟ, එම ආයෝජනයේ අනාගත වටිනාකම මාසික සංයෝගයට වඩා තරමක් වැඩි වේ. මක්නිසාද යත්, 8% පොලී අනුපාතය සෑම මාසයකම නොව සෑම දිනකම මූලික මුදලට පොලී එකතු කරන බැවිනි. ඔබට අනුමාන කළ හැකි පරිදි, මාසික සංයෝග ප්‍රතිඵලය වාර්ෂික සංයෝගයට වඩා වැඩි වනු ඇත.

  මේ සියල්ල හොඳයි, නමුත් ඔබට ඇත්තටම අවශ්‍ය වන්නේ සංයුක්ත පොලී සඳහා Excel සූත්‍රයක් නේද? කරුණාකර තව ටිකක් මා සමඟ ඉවසන්න. දැන් අපි වඩාත් රසවත් කොටස වෙත පැමිණෙමින් සිටිමු - Excel හි ඔබේම බලවත් සහ බහුකාර්ය සංයුක්ත පොලී කැල්කියුලේටරයක් ​​ගොඩනඟා ගන්න.

  Excel හි සංයුක්ත පොලී සූත්‍රය (දිනපතා, සතිපතා, මාසික, වාර්ෂික සංයෝග කිරීම)

  සාමාන්‍යයෙන් , Excel හි යමක් කිරීමට ක්‍රම එකකට වඩා ඇති අතර සංයුක්ත පොලී සූත්‍රයක් ව්‍යතිරේකයක් නොවේ :) Microsoft Excel විසින් සංයුක්ත පොලී ගණනය කිරීම සඳහා විශේෂ කාර්යයක් ලබා නොදෙන නමුත්, ඔබට ඔබේම සංයුක්ත පොලී කැල්කියුලේටරය නිර්මාණය කිරීමට වෙනත් කාර්යයන් භාවිතා කළ හැක.

  අපි Excel වැඩ පත්‍රිකාවක ආයෝජනයක අනාගත වටිනාකම තීරණය කරන මූලික සාධක ඇතුළත් කරමින් අපගේ Excel සංයුක්ත පොලී කැල්කියුලේටරය නිර්මාණය කිරීම ආරම්භ කරමු:

  • මුල් ආයෝජනය (B3)
  • වාර්ෂික පොලී අනුපාතය(B4)
  • වසරකට සංයුති කාල ගණන (B5)
  • වසර ගණන (B6)

  කළ විට, ඔබේ Excel පත්‍රය මෙයට සමාන විය හැක :

  

  ඔබට දැන් අවශ්‍ය වන්නේ ආදාන අගයන් මත පදනම්ව උපයාගත් මුදල (ශේෂය) ගණනය කිරීම සඳහා සංයුක්ත පොලී සූත්‍රය පමණි. හොඳම ආරංචිය නම් ඔබ රෝදය නැවත සොයා ගැනීමට අවශ්‍ය නොවන බවයි. අපි බැංකු සහ අනෙකුත් මුල්‍ය ආයතන විසින් භාවිතා කරන කාල පරික්ෂා කරන ලද සංයුක්ත පොලී සූත්‍රය ගෙන එය Excel භාෂාවට පරිවර්තනය කරන්නෙමු.

  Excel සඳහා සංයුක්ත පොලී සූත්‍රය:

  මුල ආයෝජන * (1 + වාර්ෂික පොලී අනුපාතය / වසරකට සංයුක්ත කාලසීමාවන් ) ^ ( වසර * වසරකට සංයුක්ත කාලපරිච්ඡේද )

  ඉහත මූලාශ්‍ර දත්ත සඳහා, සූත්‍රය මෙම හැඩය ගනී:

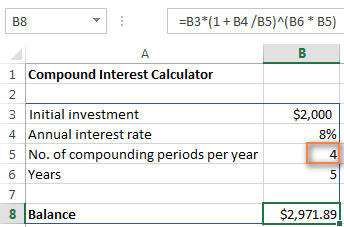
  =B3 * (1 + B4 /B5) ^ (B6 * B5)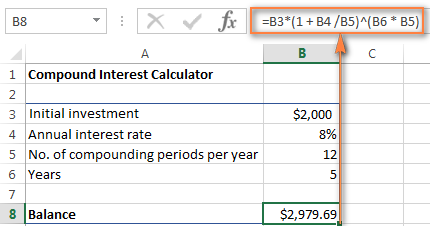

  

  සංඛ්‍යා තරමක් හුරුපුරුදු බව පෙනේද? ඔව්, මේවා අපි මාසික සංයුක්ත පොලී සූත්‍රයක් සමඟ සිදු කර ඇති එකම අගයන් සහ ගණනය කිරීම් වන අතර, ප්‍රතිඵලය ඔප්පු කරන්නේ අප සියල්ල නිවැරදිව කළ බව ය!

  ඔබට ඔබේ ආයෝජනය කොපමණ වටිනවාද යන්න දැන ගැනීමට අවශ්‍ය නම් 8% ක වාර්ෂික පොලී අනුපාතයක් කාර්තුවකට සංයුති, සරලව 4 කොටුව B5 ඇතුළත් කරන්න:

  

  ඔබේ ආයෝජනයේ අනාගත වටිනාකම අර්ධ සමඟ ගණනය කිරීමට -වාර්ෂික සංයෝග කිරීම, වසරකට සංයෝජන කාල අගය ලෙස 2 ඇතුළත් කරන්න. සතිපතා පොලී අනුපාත සඳහා, 52 ඇතුළත් කරන්න, සෑම වසරකම සති කීයක් අඩංගු වේ. ඔබ උනන්දු වන්නේ නම් දිනපතා සංයෝග කිරීම, 365 ඇතුළු කරන්න, යනාදිය.

  උපයා ඇති පොලී ප්‍රමාණය සොයා ගැනීමට , සරලව අනාගත අගය (ශේෂය) සහ වර්තමානය අතර වෙනස ගණනය කරන්න. වටිනාකම (මුල් ආයෝජනය). අපගේ නඩුවේදී, B9 හි ​​සූත්‍රය සරල ය:

  =B8-B3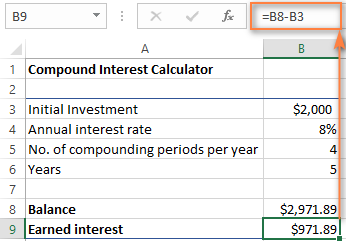

  

  ඔබට පෙනෙන පරිදි, අපි සත්‍ය වශයෙන්ම විශ්වීය සංයුක්ත පොලී කැල්කියුලේටරයක් ​​නිර්මාණය කර ඇත. එක්සෙල්. මූල්‍ය සැලසුම්කරුවන් විසින් භාවිතා කරන උපක්‍රමශීලී සංයුක්ත පොලී සූත්‍රය සොයා ගැනීමට ඔබ වටිනා මිනිත්තු කිහිපයක් ආයෝජනය කිරීම ගැන දැන් ඔබට පසුතැවීමක් නැත. ඉහත ප්‍රවේශය ගැන ඔබ එතරම් සතුටු වන්නේ නැත, Excel 2000 සිට 2019 දක්වා සියලුම අනුවාදවල ඇති FV ශ්‍රිතය භාවිතයෙන් ඔබට ඔබේ Excel සංයුක්ත පොලී කැල්කියුලේටරය නිර්මාණය කළ හැක.

  FV ශ්‍රිතය ආයෝජනයක අනාගත වටිනාකම ගණනය කරයි. අපි සාකච්ඡා කළ ඒවාට සමාන ආදාන දත්ත මත පදනම්ව, එහි වාක්‍ය ඛණ්ඩය තරමක් වෙනස් වුවද:

  FV(අනුපාතය, nper, pmt, [pv], [type])

  තර්කවල සවිස්තරාත්මක පැහැදිලි කිරීම Excel FV function tutorial හි සොයා ගත හැක.

  මේ අතරතුර, මාසික සංයුක්ත පොලී උදාහරණයේ ඇති මූලාශ්‍ර දත්ත භාවිතා කර FV සූත්‍රයක් ගොඩනඟා අපට එම ප්‍රතිඵලයම ලැබේදැයි බලමු.

  ඔබට මතක ඇති පරිදි, අපි ඩොලර් 2,000 ක් වසර 5 ක් සඳහා ඉතුරුම් ගිණුමකට 8% වාර්ෂික පොලී අනුපාතයකට මාසිකව එකතු කළෙමු. අමතර ගෙවීම් නොමැතිව. ඉතින්, අපේ