Kennsluefnið útskýrir vaxtasamsetta formúlu fyrir Excel og gefur dæmi um hvernig á að reikna út framtíðarvirði fjárfestingarinnar á árlegum, mánaðarlegum eða daglegum vöxtum. Þú munt einnig finna ítarleg skref til að búa til þinn eigin E xcel vaxtasamsetta reiknivél.

Vaxtasamsettir vextir eru ein af grunnbyggingum í bankastarfsemi og ein öflugasta fjármálastarfsemi kraftar í kringum þig sem ráða niðurstöðu fjárfestinga þinna.

Nema þú sért útskrifaður í bókhaldi, fjármálasérfræðingur eða reyndur fjárfestir gæti verið svolítið erfitt að átta sig á hugmyndinni úr sérhæfðum fjármálabókum og handbókum. Markmið þessarar greinar er að gera það auðvelt :) Þú munt einnig læra hvernig á að nota vaxtasamsetta formúlu í Excel og búa til alhliða reiknivél fyrir vaxtasamsetta vexti fyrir eigin vinnublöð.

Hvað eru vextir samsettir?

Í mjög einföldu máli eru vextir samsettir vextir sem aflað er af vöxtum. Nánar tiltekið, samsettir vextir fást bæði af upphaflegri innborgun (höfuðstól) og vöxtum sem safnast hafa frá fyrri tímabilum.

Kannski gæti verið auðveldara að byrja á einföldum vöxtum sem eru eingöngu reiknaðir á höfuðstól. Til dæmis seturðu $10 inn á bankareikning. Hvers virði mun innborgun þín vera eftir eitt ár á 7% ársvöxtum? Svarið er $10,70 (10 + 10*0,07 =vaxtasamsett formúla er sem hér segir:

=FV(0.08/12, 5*12, ,-2000)

Ef þú þarft einhverja útskýringu á breytunum, þá ferðu:

• hlutfallið er 0,008/12 þar sem þú hefur 8% ársvextir samanlagðir mánaðarlega.
• nper er 5*12, þ.e. 5 ár * 12 mánuðir
• pmt er skilið eftir autt vegna þess að við höfum engar aukagreiðslur.
• pv er -2000 þar sem það er útflæði og ætti að vera táknað með neikvæðri tölu.

Sláðu inn formúluna hér að ofan í tómt hólf og það mun gefa út $2.979,69 sem niðurstaðan (sem er fullkomlega í takt við niðurstaða stærðfræðiútreiknings sem framkvæmd var í dæminu um mánaðarlega samsetta vexti).

Að sjálfsögðu kemur ekkert í veg fyrir að þú skipta út gildunum fyrir tilvísanir í reit:

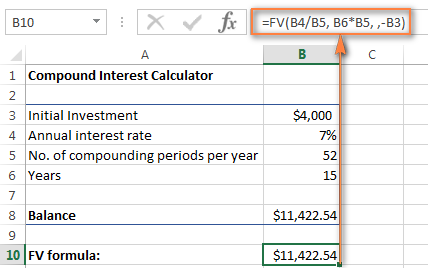
=FV(B4/B5, B6*B5, , -B3)

Skjámyndin hér að neðan sýnir framtíðarvirði $4.000 fjárfestingar eftir 15 ár á 7% árlegum vöxtum vikulega:

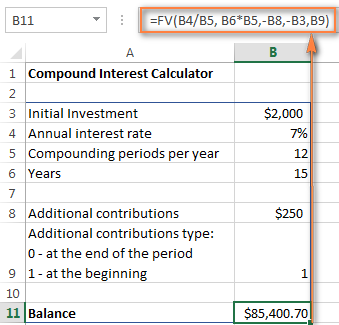
Til að gera Excel vaxtareiknivélina enn öflugri geturðu framlengt hann með Viðbótarframlögum valkostinum n (viðbótargreiðslur) og breyttu vaxtasamsettu formúlunni í samræmi við það.

=FV(B4/B5, B6*B5, -B8, -B3, B9)

Hvar:

• B3 - höfuðstólsfjárfesting
• B4 - árleg vextir
• B5 - fjöldi samsettra tímabila á ári
• B6 - fjöldi ára til að spara
• B8 - viðbótarframlög (valfrjálst)
• B9 - tegund viðbótarframlaga. Mundu að þú slærð inn 1 ef þú leggur innviðbótarfjárhæð í upphafi samsetningartímabils, 0 eða sleppt ef aukagreiðslur eru inntar af hendi í lok tímabilsins.

Ef þú hefur áhuga á að prófa þetta háþróaður reiknivél fyrir vaxtasamsetta vexti fyrir Excel til að reikna út sparnað þinn, þú getur halað honum niður í lok þessarar færslu.

Ábending. Önnur fljótleg leið til að reikna út samsetta vexti er með því að gera What-If greiningu með hjálp Excel gagnatöflu.

Vaxtasamsettir reiknivélar á netinu

Ef þú vilt frekar fjárfesta peninga en tíma í að finna út hvernig til að reikna út samsetta vexti í Excel, geta netsamsett vaxtareiknivél komið sér vel. Þú getur fundið fullt af þeim með því að slá inn eitthvað eins og "samsett vaxtareiknivél" í valinn leitarvél. Í millitíðinni leyfi ég mér að kynna í fljótu bragði nokkra af mínum uppáhalds.

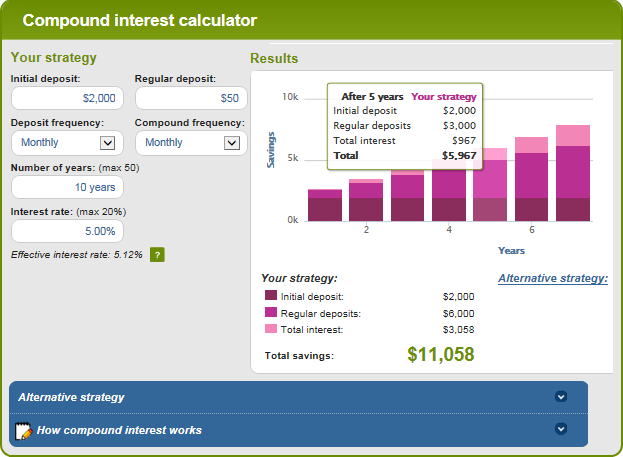
Vaxtasamsett reiknivél frá Bankrate

Helstu kostir Bankrate samsettra vaxta reiknivélarinnar eru auðveld í notkun og sjónræn framsetning á niðurstöðurnar. Þessi reiknivél gerir þér kleift að slá inn sparnaðarinntak handvirkt í reiti eða með því að færa sleðann. Þegar þú gerir þetta birtist áætluð heildarfjölda efst og endurspeglast strax í línuritinu hér að neðan:

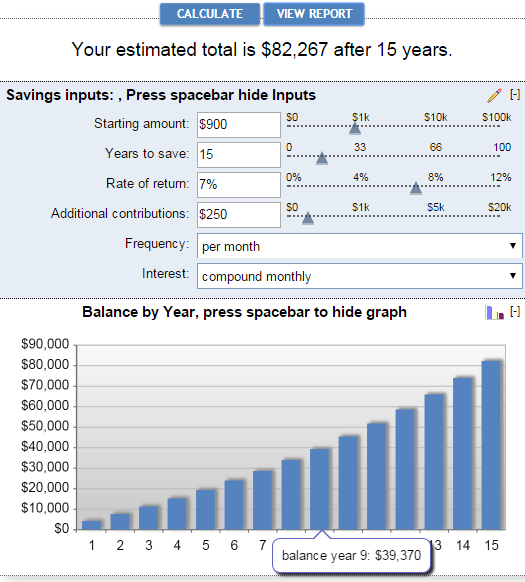
Þegar þú smellir á hnappinn Skoða skýrslu myndast "Yfirlit" Skýrsla" sem og "sparnaðarjöfnuður" sem veitir nákvæmar upplýsingar um upphæð viðbótarframlaga, áunna vexti og stöðufyrir hvert ár.

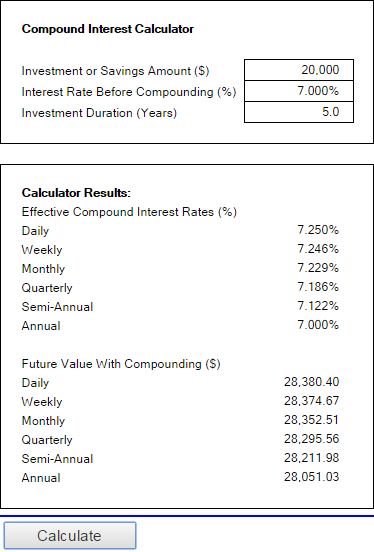
Vaxtareiknivél frá Money-Zine

Netreiknivélin frá Money-Zine er mun einfaldari miðað við þann sem Bankrate er. Það biður þig um að tilgreina aðeins 3 gildi: aðalfjárfestingu, vexti og tímalengd. Um leið og þú gefur upp þessar tölur og smellir á hnappinn Reikna út mun hann sýna þér allar tegundir samsettra vaxta (daglega, vikulega, mánaðarlega, árlega osfrv.) sem og framtíðargildi með tilheyrandi samsettur.

Vaxtasamsett reiknivél frá MoneySmart

Þetta er mjög fín reiknivél á netinu sem rekin er af Australian Securities and Investments Commission. Það gerir þér kleift að setja inn alla viðeigandi þætti sem ákvarða framtíðarvirði fjárfestingar þinnar og gefur út niðurstöðuna sem línurit. Með því að sveima yfir ákveðna stiku í línuritinu geturðu séð samantektarupplýsingarnar fyrir það tiltekna ár.

Svona reiknarðu samsetta vexti í Excel og utan þess :) Ég vona að að minnsta kosti ein formúla með vöxtum sem fjallað er um í þessari grein hafi reynst þér gagnleg. Engu að síður, ég þakka þér fyrir lesturinn og vonast til að sjá þig á blogginu okkar í næstu viku!

Æfingabók til niðurhals

Vaxtaútreikningur fyrir Excel (.xlsx skrá)

Ef um er að ræða samsetta vexti er höfuðstóllinn mismunandi á hverju tímabili. Bankinn mun ekki gefa þér áunna vexti til baka, heldur bæta þeir þeim við aðalfjárfestingu þína. Þessi aukna upphæð verður höfuðstóll fyrir næsta tímabil (samsett tímabil) og fær einnig vexti. Með öðrum orðum, þú færð ekki aðeins vexti af höfuðstólnum heldur einnig af þeim vöxtum sem aflað er á hverju samsettu tímabili.

Í okkar dæmi, auk höfuðstólsins $10, munu áunnin vextir $0,70 einnig ávaxta á næsta ári. Svo, hversu mikið mun $10 innborgun þín vera virði eftir 2 ár á árlegum vöxtum sem eru 7% samsettir árlega? Svarið er $11,45 (10,7 + 10,7*0,07 = 11,45) og áunnir vextir eru $1,45. Eins og þú sérð, í lok annars árs, þénaðiðu ekki aðeins $0,70 á fyrstu $10 innborguninni, þú þénaðir líka $0,05 á $0,70 vöxtunum sem söfnuðust á fyrsta ári.

Það eru nokkrar leiðir til að reikna út samsetta vexti í Excel og við ætlum að fjalla ítarlega um hverja og eina.

Hvernig á að reikna út samsetta vexti í Excel

Langtímafjárfestingar getur verið áhrifarík aðferð til að auka auð þinn og jafnvel lítil innlán geta skipt miklu máli með tímanum. Excel-samsettu vaxtaformúlurnar sem útskýrðar eru frekar munu hjálpa þér að ná sparnaðarstefnunni tilvinna. Að lokum ætlum við að búa til alhliða formúlu sem reiknar út framtíðargildi með mismunandi samsettu tímabilum - daglega, vikulega, mánaðarlega, ársfjórðungslega eða árlega.

Reiknar út árlega vexti í Excel

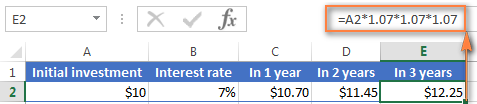
Til að skilja hugmyndina um vaxtasamsetta betur, byrjum á mjög einföldu dæmi sem fjallað er um í upphafi þessa kennsluefnis og skrifum formúlu til að reikna út árlega vexti í Excel. Eins og þú manst þá ertu að fjárfesta $10 á 7% árlegum vöxtum og vilt vita hvernig árleg samsetning eykur sparnað þinn.

Árlegir vextir - formúla 1

Auðveld og einföld leið til að reikna út upphæðina sem aflað er með árlegum vöxtum er að nota formúluna til að hækka tölu um prósentu:

=Amount * (1 + %) .

Í dæminu okkar er formúlan:

=A2*(1+$B2)

Þar sem A2 er upphafleg innborgun þín og B2 eru ársvextir. Vinsamlegast athugaðu að við lagfærum tilvísunina í dálk B með því að nota $ táknið.

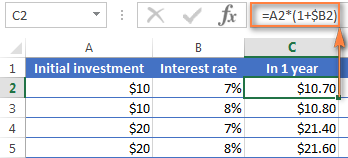
Eins og þú manst er 1% einn hluti af hundrað, þ.e. 0,01, svo 7 % er 0,07 og þannig eru prósentur í raun geymdar í Excel. Með þetta í huga geturðu staðfest niðurstöðuna sem formúlan skilar með því að framkvæma einfaldan útreikning á 10*(1+0,07) eða 10*1,07 og ganga úr skugga um að staðan þín eftir 1 ár verði $10,70 örugglega.

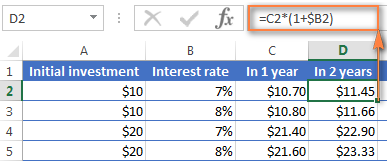
Og nú skulum við reikna stöðuna eftir 2 ár. Svo hvernigmun $10 innborgun þín vera mikils virði eftir tvö ár með 7% ársvöxtum? Svarið er $11,45 og þú getur fengið það með því að afrita sömu formúlu í dálk D.

Til að reikna út hversu mikið fé þú finnur á bankareikningnum þínum í lok 3. ár, einfaldlega afritaðu sömu formúluna í dálk E og þú færð $12.25.

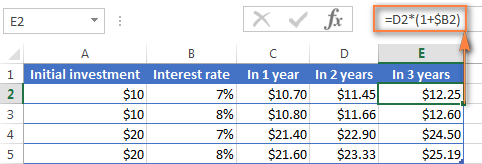
Þið sem hafið reynslu af Excel formúlum hafið líklega fundið út að það sem ofangreind formúla í raun er að margfalda fyrstu innborgunina upp á $10 með 1,07 þrisvar sinnum:

=10*1.07*1.07*1.07=12.25043

Aðrunda það að tveimur aukastöfum og þú færð sömu tölu og þú sérð í reit E2 á skjámyndinni hér að ofan - $12,25. Auðvitað er hægt að reikna út stöðuna beint eftir 3 ár með þessari formúlu:

=A2*1.07*1.07*1.07

Árlegir vextir - formúla 2

Annað leiðin til að búa til árlega samsetta vaxtaformúlu er að reikna áunna vexti fyrir hvert ár og bæta þeim síðan við upphafsinnborgunina.

Að því gefnu að upphafleg innborgun sé í reit B1 og Ársvextir í reit B2, eftirfarandi formúla virkar gott:

=B1 + B1 * $B$2

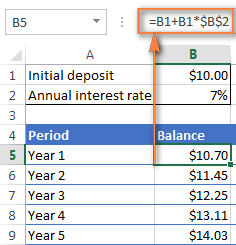
Til að formúlan virki rétt skaltu hafa í huga að eftirfarandi upplýsingar:

• Leggaðu tilvísunina í Ársvexti reitinn (B2 í okkar tilfelli) með því að bæta við $ tákninu, það ætti að vera alger dálkur og alger röð, eins og $B$2.
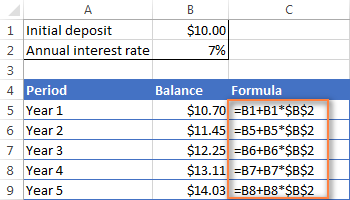
• Fyrir 2. ár (B6)og öll síðari ár, breyttu formúlunni í:

  Ár 1 staða + Ár 1 staða * Vextir

Í þessu dæmi myndirðu slá inn eftirfarandi formúlu í reit B6 og afritaðu það síðan niður í aðrar línur, eins og sýnt er á skjámyndinni hér að neðan:

=B5 + B5 * $B$2

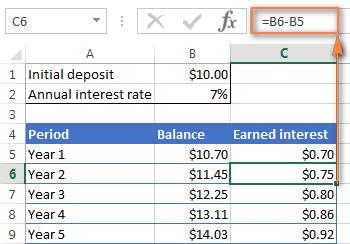
Til að komast að því hversu mikla vexti þú fékkst í raun með árlegri samsetningu, draga upphaflega innborgun (B1) frá stöðu eftir 1 ár (B5). Þessi formúla fer í C5:

=B5-B1

Í C6 skaltu draga Staða eftir 1 ár frá Staða eftir 2 ár og draga formúluna niður til annarra frumna:

=B6-B5

Þú ættir að sjá áunna vexti vöxt eins og á skjámyndinni hér að neðan.

Dæmin hér að ofan skila vel hugmyndinni um samsetta vexti, er það ekki? En engin formúlanna er nógu góð til að vera kölluð alhliða vaxtasamsett formúla fyrir Excel. Í fyrsta lagi vegna þess að þeir leyfa þér ekki að tilgreina samsetningartíðni og í öðru lagi vegna þess að þú þarft að byggja upp heila töflu frekar en að slá bara inn ákveðna tímalengd og vexti.

Jæja, við skulum taka skref fram á við og búa til alhliða vaxtasamsett formúla fyrir Excel sem getur reiknað út hversu mikið fé þú færð með árlegum, ársfjórðungslegum, mánaðarlegum, vikulegum eða daglegum samsetningu.

Almenn formúla vaxtasamsettra vaxta

Þegar fjármálaráðgjafar greina áhrifin af samsettum vöxtum áfjárfestingu, taka þeir venjulega til greina þrjá þætti sem ákvarða framtíðarvirði fjárfestingarinnar (FV):

• PV - núvirði fjárfestingarinnar
• i - vextir aflað á hverju tímabili
• n - fjöldi tímabila

Með því að þekkja þessa þætti er hægt að nota eftirfarandi formúlu til að fá framtíðarvirði fjárfestingarinnar með ákveðnum samsettum vöxtum :

Til að útskýra málið betur eru hér nokkur fljótleg dæmi.

Dæmi 1: Formúla mánaðarlegrar vaxtasamsettra vaxta

Segjum sem svo að þú fjárfestir $2.000 á 8% vöxtum mánaðarlega og þú vilt vita verðmæti fjárfestingar þinnar eftir 5 ár.

Fyrst skulum við skrifa niður lista yfir íhluti fyrir samsetta vaxtaformúlu þína:

• PV = $2.000
• i = 8% á ári, samansett mánaðarlega (0,08/12= 006666667)
• n = 5 ár x 12 mánuðir (5*12= 60)

Sláðu inn ofangreindar tölur í formúluna og þú færð:

= $2,000 * (1 + 0.8/12)5x12

eða

= $2,000 * 1.00666666760

eða

= $2,000 * 1.489845708 = $2,979.69

Dæmi 2: Formúla daglegra vaxtasamsettra vaxta

Ég vona að dæmið um mánaðarlega vaxtasamsetningu sé vel skilið og nú er hægt að nota sömu nálgun fyrir daglega samsetningu. Upphafsfjárfesting, vextir, tímalengd og formúlan eru nákvæmlega þau sömu og í dæminu hér að ofan, aðeins samsetningartímabilið er öðruvísi:

• PV = $2.000
• i = 8% á ári, samanlagt daglega(0,08/365 = 0,000219178)
• n = 5 ár x 365 dagar (5*365 =1825)

Setjið ofangreindar tölur inn í vaxtasamsetta formúluna og þú munt fá eftirfarandi niðurstaða:

=$2,000 * (1 + 0.000219178)1825 = $2,983.52

Eins og þú sérð, með daglegum vöxtum, er framtíðarvirði sömu fjárfestingar aðeins hærra en með mánaðarlegri samsetningu. Þetta er vegna þess að 8% vextirnir bæta vöxtum við höfuðstól á hverjum degi frekar en í hverjum mánuði. Eins og þú getur giskað á, verður mánaðarleg samsetning niðurstaða hærri en árleg samsetning.

Allt þetta er gott, en það sem þú vilt í raun er Excel formúla fyrir samsetta vexti, ekki satt? Vertu bara með mig aðeins lengur, takk. Nú erum við að komast að áhugaverðasta hlutanum - að byggja upp þinn eigin öfluga og fjölhæfa vaxtasamsetta reiknivél í Excel.

Vaxtasamsett formúla í Excel (daglega, vikulega, mánaðarlega, árlega samsetningu)

Venjulega , það eru fleiri en ein leið til að gera eitthvað í Excel og vaxtasamsett formúla er engin undantekning :) Þó að Microsoft Excel veiti enga sérstaka aðgerð til að reikna út vaxtasamsetta vexti geturðu notað önnur föll til að búa til þinn eigin vaxtasamsetta reiknivél.

Við skulum byrja að búa til Excel vaxtareiknivélina okkar með því að slá inn grunnþætti sem ákvarða framtíðarvirði fjárfestingar í Excel vinnublaði:

• upphafsfjárfesting (B3)
• ársvextir(B4)
• fjöldi samsettra tímabila á ári (B5)
• fjöldi ára (B6)

Þegar þessu er lokið gæti Excel blaðið þitt litið svipað út og þetta :

Allt sem þú þarft núna er vaxtasamsett formúla til að reikna áunna upphæð (Balance) út frá inntaksgildunum. Bestu fréttirnar eru þær að þú þarft ekki að finna upp hjólið upp á nýtt. Við tökum einfaldlega hina tímaprófuðu vaxtasamsettu formúlu sem notuð er af banka og öðrum fjármálastofnunum og þýðum hana yfir á tungumál Excel.

Vaxtasamsettir formúlur fyrir Excel:

Fyrir ofangreind upprunagögn tekur formúlan þessa mynd:

=B3 * (1 + B4 /B5) ^ (B6 * B5)

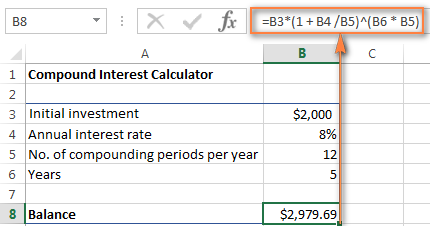
Tölurnar virðast frekar kunnuglegar? Já, þetta eru sömu gildi og útreikningar og við höfum framkvæmt með mánaðarlegri vaxtaformúlu, og niðurstaðan sannar að við gerðum allt rétt!

Ef þú vilt vita hversu mikils virði fjárfestingin þín verður á 8% ársvextir samsettir á ársfjórðungslega , sláðu einfaldlega inn 4 í reit B5:

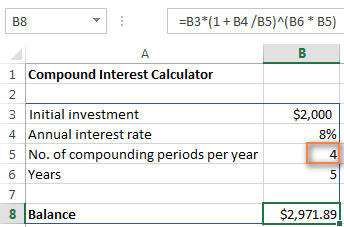
Til að reikna út framtíðarvirði fjárfestingar þinnar með semi -árleg samsetning, sláðu inn 2 sem samsett tímabil á ári gildi. Fyrir vikulega vexti skal slá inn 52, þetta er hversu margar vikur hvert ár inniheldur. Ef þú hefur áhuga á dagleg samsetning, sláðu inn 365, og svo framvegis.

Til að finna upphæð unninna vaxta , reiknaðu einfaldlega mismuninn á milli framtíðarvirðis (staða) og núverandi verðmæti (upphaflega fjárfesting). Í okkar tilviki er formúlan í B9 eins einföld og:

=B8-B3

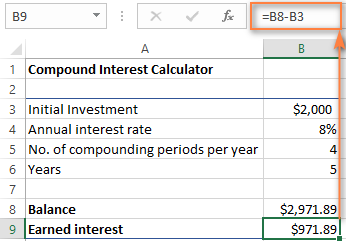
Eins og þú sérð höfum við búið til raunverulegan alhliða reiknivél fyrir vaxtasamsetta vexti fyrir Excel. Vonandi sérðu nú ekki eftir því að þú hafir fjárfest nokkrar dýrmætar mínútur í að finna út hina erfiðu vaxtasamsettu formúlu sem fjármálaskipuleggjendur nota: )

Ítarlegri reiknivél fyrir vaxtasamsetta vexti fyrir Excel

Ef af einhverjum ástæðum þú ert ekki alveg ánægður með ofangreinda nálgun, þú getur búið til Excel vaxtareiknivélina þína með því að nota FV fallið sem er fáanlegt í öllum útgáfum Excel 2000 til 2019.

FV fallið reiknar út framtíðarvirði fjárfestingar byggt á inntaksgögnum sem eru svipuð þeim sem við höfum fjallað um, þó setningafræði þeirra sé aðeins önnur:

Ítarleg útskýring á rökunum er að finna í Excel FV fallkennslunni.

Í millitíðinni skulum við búa til FV formúlu með því að nota sömu upprunagögn og í dæmi um mánaðarlega vexti og sjá hvort við fáum sömu niðurstöðu.

Eins og þú manst þá lögðum við 2.000 dali í 5 ár inn á sparnaðarreikning á 8% ársvöxtum samansettum mánaðarlega, án aukagreiðslu. Svo, okkar