ટ્યુટોરીયલ એક્સેલ માટે ચક્રવૃદ્ધિ વ્યાજ સૂત્ર સમજાવે છે અને વાર્ષિક, માસિક અથવા દૈનિક ચક્રવૃદ્ધિ વ્યાજ દરે રોકાણના ભાવિ મૂલ્યની ગણતરી કેવી રીતે કરવી તેના ઉદાહરણો પ્રદાન કરે છે. તમને તમારું પોતાનું E xcel ચક્રવૃદ્ધિ વ્યાજ કેલ્ક્યુલેટર બનાવવા માટેના વિગતવાર પગલાં પણ મળશે.

ચક્રવૃદ્ધિ વ્યાજ એ બેંકિંગમાં મૂળભૂત બિલ્ડીંગ બ્લોક્સમાંનું એક છે અને સૌથી શક્તિશાળી નાણાકીય છે. તે તમારા રોકાણના પરિણામને નિર્ધારિત કરે છે.

જ્યાં સુધી તમે એકાઉન્ટિંગ ગ્રેજ્યુએટ, નાણાકીય વિશ્લેષક અથવા અનુભવી રોકાણકાર ન હોવ, તો વિશિષ્ટ નાણાકીય પુસ્તકો અને માર્ગદર્શિકાઓમાંથી ખ્યાલને સમજવો થોડો મુશ્કેલ હોઈ શકે છે. આ લેખનો ઉદ્દેશ્ય તેને સરળ બનાવવાનો છે : ) તમે એક્સેલમાં ચક્રવૃદ્ધિ વ્યાજ સૂત્રનો ઉપયોગ કેવી રીતે કરવો અને તમારી પોતાની વર્કશીટ્સ માટે સાર્વત્રિક સંયોજન વ્યાજ કેલ્ક્યુલેટર કેવી રીતે બનાવવું તે પણ શીખી શકશો.

શું ચક્રવૃદ્ધિ વ્યાજ છે?

ખૂબ જ સરળ શબ્દોમાં, ચક્રવૃદ્ધિ વ્યાજ એ વ્યાજ પર મેળવેલ વ્યાજ છે. વધુ સ્પષ્ટ રીતે કહીએ તો, પ્રારંભિક ડિપોઝિટ (મૂળ) અને અગાઉના સમયગાળાથી સંચિત વ્યાજ બંને પર ચક્રવૃદ્ધિ વ્યાજ મળે છે.

કદાચ, ફક્ત મૂળ રકમ પર ગણવામાં આવતા સાદા વ્યાજ સાથે પ્રારંભ કરવાનું વધુ સરળ હોઈ શકે છે. ઉદાહરણ તરીકે, તમે બેંક ખાતામાં $10 મૂકો છો. એક વર્ષ પછી 7% ના વાર્ષિક વ્યાજ દરે તમારી થાપણની કિંમત કેટલી હશે? જવાબ છે $10.70 (10 + 10*0.07 =ચક્રવૃદ્ધિ વ્યાજ સૂત્ર નીચે મુજબ છે:

=FV(0.08/12, 5*12, ,-2000)

જો તમને પરિમાણોની થોડી સમજૂતીની જરૂર હોય, તો તમે અહીં જાઓ:

• દર 0.008/12 છે કારણ કે તમારી પાસે છે 8% વાર્ષિક વ્યાજ દર માસિક ચક્રવૃદ્ધિ થાય છે.
• nper 5*12 છે, એટલે કે 5 વર્ષ * 12 મહિના
• pmt ખાલી છે કારણ કે અમારી પાસે કોઈ વધારાની ચૂકવણી નથી.
• pv છે -2000 કારણ કે તે એક આઉટફ્લો છે અને તેને નકારાત્મક સંખ્યા દ્વારા દર્શાવવું જોઈએ.

ખાલી કોષમાં ઉપરોક્ત સૂત્ર દાખલ કરો, અને તે પરિણામ તરીકે $2,979.69 નું આઉટપુટ કરશે (જે સંપૂર્ણ રીતે ઈનલાઈન છે. માસિક ચક્રવૃદ્ધિ વ્યાજના ઉદાહરણમાં કરવામાં આવેલ ગણિતની ગણતરીનું પરિણામ).

સ્વાભાવિક રીતે, તમને મૂલ્યોને સેલ સંદર્ભો સાથે બદલવાથી કંઈપણ અટકાવતું નથી:

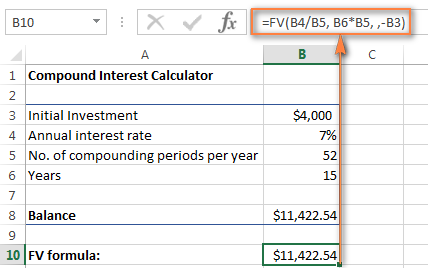
=FV(B4/B5, B6*B5, , -B3)

નીચેનો સ્ક્રીનશોટ બતાવે છે 7% ચક્રવૃદ્ધિ સાપ્તાહિક વાર્ષિક વ્યાજ દરે 15 વર્ષ પછી $4,000 રોકાણનું ભાવિ મૂલ્ય:

તમારા એક્સેલ સંયોજન વ્યાજ કેલ્ક્યુલેટરને વધુ શક્તિશાળી બનાવવા માટે, તમે તેને વિસ્તૃત કરી શકો છો વધારાના યોગદાન વિકલ્પ સાથે n (વધારાની ચૂકવણી) અને તે મુજબ ચક્રવૃદ્ધિ વ્યાજ સૂત્રમાં ફેરફાર કરો.

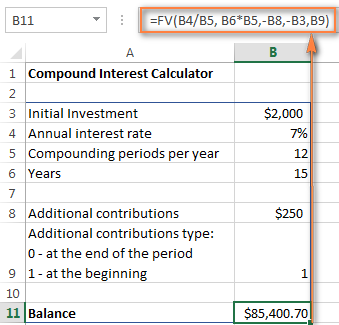
=FV(B4/B5, B6*B5, -B8, -B3, B9)

ક્યાં:

• B3 - મુખ્ય રોકાણ
• B4 - વાર્ષિક વ્યાજ દર
• B5 - પ્રતિ વર્ષ ચક્રવૃદ્ધિ સમયગાળાની સંખ્યા
• B6 - બચાવવા માટેના વર્ષોની સંખ્યા
• B8 - વધારાના યોગદાન (વૈકલ્પિક)
• B9 - વધારાના યોગદાનનો પ્રકાર. યાદ રાખો કે જો તમે જમા કરો છો તો તમે 1 દાખલ કરો છોચક્રવૃદ્ધિ અવધિની શરૂઆતમાં વધારાની રકમ, 0 અથવા અવગણવામાં આવે છે જો સમયગાળાના અંતે વધારાની ચૂકવણી કરવામાં આવે છે.

જો તમે આ અજમાવવા માટે ઉત્સુક છો તમારી બચતની ગણતરી કરવા માટે એક્સેલ માટે એડવાન્સ્ડ કમ્પાઉન્ડ ઈન્ટરેસ્ટ કેલ્ક્યુલેટર, તમે તેને આ પોસ્ટના અંતે ડાઉનલોડ કરી શકો છો.

ટીપ. ચક્રવૃદ્ધિ વ્યાજની ગણતરી કરવાની બીજી ઝડપી રીત એ છે કે એક્સેલ ડેટા ટેબલની મદદથી શું-જો વિશ્લેષણ કરવું.

કમ્પાઉન્ડ ઈન્ટરેસ્ટ કેલ્ક્યુલેટર ઓનલાઈન

જો તમે કેવી રીતે તે શોધવામાં સમયને બદલે નાણાંનું રોકાણ કરવાનું પસંદ કરો છો એક્સેલમાં ચક્રવૃદ્ધિ વ્યાજની ગણતરી કરવા માટે, ઓનલાઈન ચક્રવૃદ્ધિ વ્યાજ કેલ્ક્યુલેટર કામમાં આવી શકે છે. તમે તમારા મનપસંદ સર્ચ એન્જિનમાં "કમ્પાઉન્ડ ઈન્ટરેસ્ટ કેલ્ક્યુલેટર" જેવું કંઈક દાખલ કરીને તેમાંથી પુષ્કળ શોધી શકો છો. આ દરમિયાન, મને મારા મનપસંદ કેટલાકને ઝડપથી રજૂ કરવા દો.

બેંકરેટ દ્વારા ચક્રવૃદ્ધિ વ્યાજ કેલ્ક્યુલેટર

બેન્કરેટ ચક્રવૃદ્ધિ વ્યાજ કેલ્ક્યુલેટરના મુખ્ય ફાયદાઓ ઉપયોગમાં સરળતા અને વિઝ્યુઅલ પ્રેઝન્ટેશન છે. પરીણામ. આ કેલ્ક્યુલેટર તમને બચત ઈનપુટ્સ જાતે બોક્સમાં અથવા સ્લાઈડર ખસેડીને દાખલ કરવા દે છે. જેમ તમે આ કરો છો, અંદાજિત કુલ ટોચ પર પ્રદર્શિત થાય છે અને તરત જ નીચેના ગ્રાફમાં પ્રતિબિંબિત થાય છે:

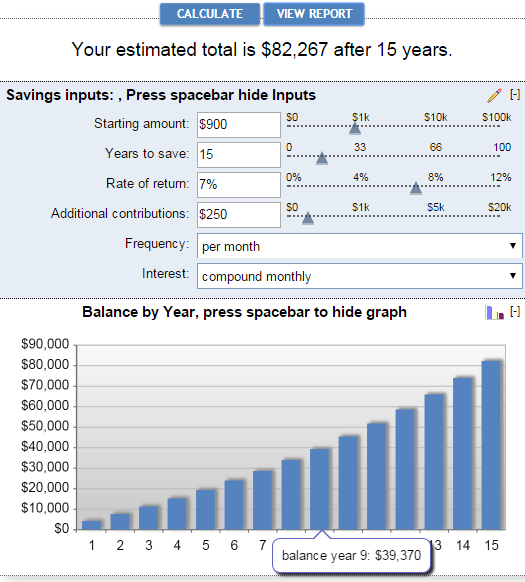
રિપોર્ટ જુઓ બટન પર ક્લિક કરવાથી "સારાંશ" જનરેટ થાય છે રિપોર્ટ" તેમજ "બચત બેલેન્સ" જે વધારાના યોગદાનની રકમ, કમાયેલ વ્યાજ અને સંતુલન વિશે વિગતવાર માહિતી પ્રદાન કરે છેદરેક વર્ષ માટે.

મની-ઝાઈન દ્વારા કમ્પાઉન્ડ ઈન્ટરેસ્ટ કેલ્ક્યુલેટર

મની-ઝાઈનનું ઓનલાઈન કેલ્ક્યુલેટર બેંકરેટની સરખામણીમાં ઘણું સરળ છે. તે તમને ફક્ત 3 મૂલ્યો સ્પષ્ટ કરવા કહે છે: મુખ્ય રોકાણ, વ્યાજ દર અને અવધિ. જલદી તમે આ નંબરો સપ્લાય કરો અને ગણતરી કરો બટન પર ક્લિક કરો, તે તમને તમામ પ્રકારના ચક્રવૃદ્ધિ વ્યાજ દર (દૈનિક, સાપ્તાહિક, માસિક, વાર્ષિક, વગેરે) તેમજ અનુરૂપ ભાવિ મૂલ્યો બતાવશે. કમ્પાઉન્ડિંગ.

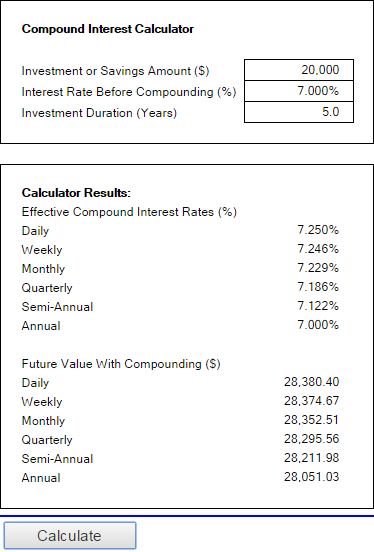
મનીસ્માર્ટ દ્વારા કમ્પાઉન્ડ ઈન્ટરેસ્ટ કેલ્ક્યુલેટર

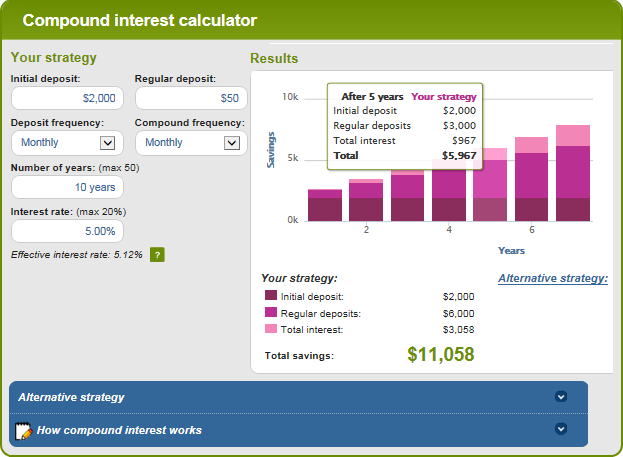
ઓસ્ટ્રેલિયન સિક્યોરિટીઝ એન્ડ ઈન્વેસ્ટમેન્ટ કમિશન દ્વારા સંચાલિત આ ખરેખર સરસ ઓનલાઈન કમ્પાઉન્ડ ઈન્ટરેસ્ટ કેલ્ક્યુલેટર છે. તે તમને તમામ સંબંધિત પરિબળોને ઇનપુટ કરવા દે છે જે તમારા રોકાણનું ભાવિ મૂલ્ય નક્કી કરે છે અને પરિણામને ગ્રાફ તરીકે આઉટપુટ કરે છે. ગ્રાફમાં ચોક્કસ બાર પર હોવર કરીને, તમે તે ચોક્કસ વર્ષ માટે સારાંશ માહિતી જોઈ શકો છો.

આ રીતે તમે Excel માં અને તેની બહાર ચક્રવૃદ્ધિ વ્યાજની ગણતરી કરો છો :) હું આશા રાખું છું કે આ લેખમાં ચર્ચા કરેલ ઓછામાં ઓછું એક ચક્રવૃદ્ધિ વ્યાજ સૂત્ર તમારા માટે ઉપયોગી સાબિત થયું છે. કોઈપણ રીતે, વાંચવા બદલ હું તમારો આભાર માનું છું અને આશા રાખું છું કે તમને આવતા અઠવાડિયે અમારા બ્લોગ પર મળીશ!

ડાઉનલોડ કરવા માટેની વર્કબુકની પ્રેક્ટિસ કરો

એક્સેલ માટે સંયોજન વ્યાજ કેલ્ક્યુલેટર (.xlsx ફાઇલ)

ચક્રવૃદ્ધિ વ્યાજ ના કિસ્સામાં, દરેક સમયગાળામાં મુદ્દલ અલગ છે. બેંક તમને કમાયેલ વ્યાજ પાછું આપશે નહીં, તેના બદલે તેઓ તેને તમારા મુખ્ય રોકાણમાં ઉમેરશે. આ વધેલી રકમ આગામી સમયગાળો (ચક્રવૃદ્ધિ અવધિ) માટે મુખ્ય બની જાય છે અને વ્યાજ પણ કમાય છે. બીજા શબ્દોમાં કહીએ તો, તમે માત્ર મૂળ રકમ પર જ નહીં, પરંતુ દરેક ચક્રવૃદ્ધિ અવધિમાં મેળવેલા વ્યાજ પર પણ વ્યાજ મેળવો છો.

અમારા ઉદાહરણમાં, $10ની મૂળ રકમ ઉપરાંત, $0.70 નું કમાયેલ વ્યાજ મળશે આવતા વર્ષે વ્યાજ પણ મેળવો. તો, વાર્ષિક 7% ચક્રવૃદ્ધિના વાર્ષિક વ્યાજ દરે 2 વર્ષ પછી તમારી $10 થાપણની કિંમત કેટલી હશે? જવાબ છે $11.45 (10.7 + 10.7*0.07 = 11.45) અને તમારું કમાવેલ વ્યાજ $1.45 છે. જેમ તમે જુઓ છો, બીજા વર્ષના અંતે, તમે પ્રારંભિક $10 ડિપોઝિટ પર માત્ર $0.70 કમાયા નથી, તમે પ્રથમ વર્ષમાં સંચિત $0.70 વ્યાજ પર $0.05 પણ કમાયા છો.

એક્સેલમાં ચક્રવૃદ્ધિ વ્યાજની ગણતરી કરવાની ઘણી રીતો છે, અને અમે દરેકની વિગતવાર ચર્ચા કરવા જઈ રહ્યા છીએ.

એક્સેલમાં ચક્રવૃદ્ધિ વ્યાજની ગણતરી કેવી રીતે કરવી

લાંબા સમયના રોકાણ તમારી સંપત્તિ વધારવા માટે એક અસરકારક વ્યૂહરચના બની શકે છે, અને નાની થાપણો પણ સમય જતાં મોટો ફરક લાવી શકે છે. એક્સેલ કમ્પાઉન્ડ ઈન્ટરેસ્ટ ફોર્મ્યુલા આગળ સમજાવવામાં આવેલ છે જે તમને બચત વ્યૂહરચના મેળવવામાં મદદ કરશેકામ આખરે, અમે એક સાર્વત્રિક સૂત્ર બનાવવા જઈ રહ્યા છીએ જે વિવિધ સંયોજન સમયગાળા સાથે ભાવિ મૂલ્યની ગણતરી કરે છે - દૈનિક, સાપ્તાહિક, માસિક, ત્રિમાસિક અથવા વાર્ષિક.

એક્સેલમાં વાર્ષિક ચક્રવૃદ્ધિ વ્યાજની ગણતરી

ચક્રવૃદ્ધિ વ્યાજના વિચારને વધુ સારી રીતે સમજો, ચાલો આ ટ્યુટોરીયલની શરૂઆતમાં ચર્ચા કરવામાં આવેલ એક ખૂબ જ સરળ ઉદાહરણથી શરૂઆત કરીએ અને Excel માં વાર્ષિક ચક્રવૃદ્ધિ વ્યાજની ગણતરી કરવા માટે એક સૂત્ર લખીએ. જેમ તમને યાદ છે, તમે 7%ના વાર્ષિક વ્યાજ દરે $10નું રોકાણ કરી રહ્યાં છો અને જાણવા માગો છો કે વાર્ષિક ચક્રવૃદ્ધિથી તમારી બચત કેવી રીતે વધે છે.

વાર્ષિક ચક્રવૃદ્ધિ વ્યાજ - ફોર્મ્યુલા 1

એક સરળ અને સીધી રીત વાર્ષિક ચક્રવૃદ્ધિ વ્યાજ સાથે મેળવેલી રકમની ગણતરી કરવા માટે સંખ્યાને ટકાવારીથી વધારવા માટે સૂત્રનો ઉપયોગ કરવામાં આવે છે:

=Amount * (1 + %) .

અમારા ઉદાહરણમાં, સૂત્ર છે:

=A2*(1+$B2)

જ્યાં A2 એ તમારી પ્રારંભિક ડિપોઝિટ છે અને B2 એ વાર્ષિક વ્યાજ દર છે. કૃપા કરીને ધ્યાન આપો કે અમે $ ચિહ્નનો ઉપયોગ કરીને કૉલમ B નો સંદર્ભ ઠીક કરીએ છીએ.

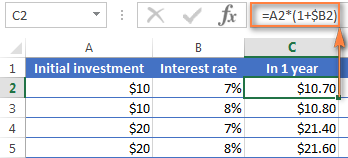
જેમ તમને યાદ છે, 1% એ સોનો એક ભાગ છે, એટલે કે 0.01, તેથી 7 % એ 0.07 છે, અને આ રીતે ટકાવારી ખરેખર Excel માં સંગ્રહિત થાય છે. આને ધ્યાનમાં રાખીને, તમે 10*(1+0.07) અથવા 10*1.07 ની સરળ ગણતરી કરીને ફોર્મ્યુલા દ્વારા પરત કરવામાં આવેલા પરિણામને ચકાસી શકો છો અને ખાતરી કરો કે 1 વર્ષ પછી તમારું બેલેન્સ ખરેખર $10.70 હશે.

અને હવે, ચાલો 2 વર્ષ પછી બેલેન્સની ગણતરી કરીએ. તો કેવી રીતે7% ના વાર્ષિક વ્યાજ દરે તમારી $10 ની થાપણ બે વર્ષમાં કેટલી કિંમતની હશે? જવાબ છે $11.45 અને તમે તે જ ફોર્મ્યુલા D કૉલમમાં કૉપિ કરીને મેળવી શકો છો.

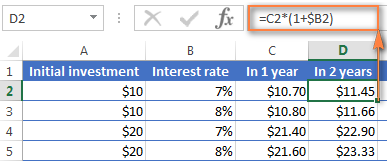
3 ના અંતે તમને તમારા બેંક ખાતામાં કેટલા પૈસા મળશે તેની ગણતરી કરવા માટે વર્ષો, ફક્ત એ જ ફોર્મ્યુલાને કૉલમ E માં કૉપિ કરો અને તમને $12.25 મળશે.

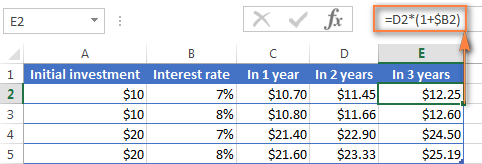
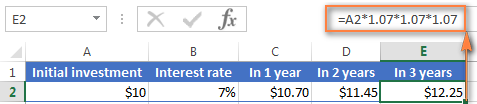
તમારામાંથી જેઓ એક્સેલ ફોર્મ્યુલાનો થોડો અનુભવ ધરાવે છે તેઓ કદાચ સમજી ગયા હશે કે ઉપરોક્ત સૂત્ર શું છે વાસ્તવમાં તે $10 ની પ્રારંભિક ડિપોઝીટને 1.07 દ્વારા ત્રણ વખત ગુણાકાર કરે છે:

=10*1.07*1.07*1.07=12.25043

તેને બે દશાંશ સ્થાનો પર રાઉન્ડ કરો અને તમને ઉપરના સ્ક્રીનશૉટમાં સેલ E2 માં જે નંબર દેખાય છે તે જ નંબર મળશે - $12.25. સ્વાભાવિક રીતે, તમે આ ફોર્મ્યુલાનો ઉપયોગ કરીને 3 વર્ષ પછી બેલેન્સની સીધી ગણતરી કરી શકો છો:

=A2*1.07*1.07*1.07

વાર્ષિક ચક્રવૃદ્ધિ વ્યાજ - ફોર્મ્યુલા 2

બીજું વાર્ષિક ચક્રવૃદ્ધિ વ્યાજની ફોર્મ્યુલા બનાવવાની રીત એ છે કે દરેક વર્ષ માટે કમાયેલા વ્યાજની ગણતરી કરવી અને પછી તેને પ્રારંભિક ડિપોઝિટમાં ઉમેરો.

માની લઈએ કે તમારી પ્રારંભિક થાપણ સેલ B1 અને <1 માં છે>વાર્ષિક વ્યાજ દર સેલ B2 માં, નીચેનું સૂત્ર એક સારવારનું કામ કરે છે:

=B1 + B1 * $B$2

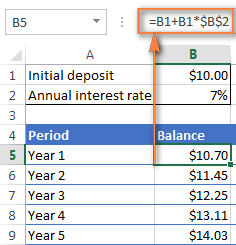
સૂત્ર યોગ્ય રીતે કાર્ય કરવા માટે, કૃપા કરીને ધ્યાનમાં લો નીચેની વિગતો:

• $ ચિહ્ન ઉમેરીને વાર્ષિક વ્યાજ દર સેલ (અમારા કિસ્સામાં B2) નો સંદર્ભ ઠીક કરો, તે સંપૂર્ણ કૉલમ અને સંપૂર્ણ પંક્તિ હોવી જોઈએ, જેમ કે $B$2.
• વર્ષ 2 (B6) માટેઅને પછીના બધા વર્ષો, ફોર્મ્યુલાને આમાં બદલો:

  વર્ષ 1 બેલેન્સ + વર્ષ 1 બેલેન્સ * વ્યાજ દર

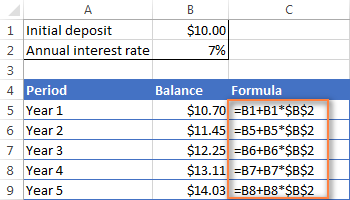
આ ઉદાહરણમાં, તમે સેલ B6 માં નીચેનું સૂત્ર દાખલ કરશો અને પછી તેને અન્ય પંક્તિઓમાં કૉપિ કરો, જેમ કે નીચેના સ્ક્રીનશૉટમાં દર્શાવવામાં આવ્યું છે:

=B5 + B5 * $B$2

વાર્ષિક ચક્રવૃદ્ધિ સાથે તમે ખરેખર કેટલું વ્યાજ મેળવ્યું છે તે શોધવા માટે, પ્રારંભિક થાપણ (B1) ને 1 વર્ષ પછીના બેલેન્સમાંથી બાદ કરો (B5). આ ફોર્મ્યુલા C5 પર જાય છે:

=B5-B1

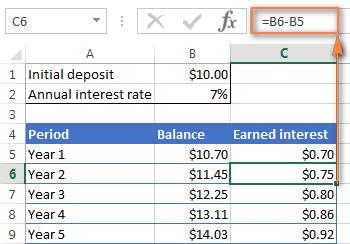
C6 માં, 2 વર્ષ પછી બેલેન્સ માંથી 1 વર્ષ પછી બેલેન્સ બાદ કરો અને ફોર્મ્યુલાને નીચે ખેંચો અન્ય કોષો માટે:

=B6-B5

તમે નીચે આપેલા સ્ક્રીનશોટની જેમ કમાવેલ વ્યાજ વૃદ્ધિ જોવી જોઈએ.

ઉપરોક્ત ઉદાહરણો ચક્રવૃદ્ધિ વ્યાજના વિચારને સમજાવતા સારું કામ કરે છે, શું તે નથી? પરંતુ એક્સેલ માટે યુનિવર્સલ કમ્પાઉન્ડ ઈન્ટરેસ્ટ ફોર્મ્યુલા કહેવા માટે કોઈપણ ફોર્મ્યુલા એટલા સારા નથી. પ્રથમ, કારણ કે તેઓ તમને સંયોજનની આવર્તનનો ઉલ્લેખ કરવા દેતા નથી, અને બીજું, કારણ કે તમારે ચોક્કસ સમયગાળો અને વ્યાજ દર દાખલ કરવાને બદલે આખું ટેબલ બનાવવું પડશે.

સારું, ચાલો એક પગલું આગળ વધીએ અને બનાવીએ. એક્સેલ માટે એક સાર્વત્રિક ચક્રવૃદ્ધિ વ્યાજ સૂત્ર કે જે તમે વાર્ષિક, ત્રિમાસિક, માસિક, સાપ્તાહિક અથવા દૈનિક ચક્રવૃદ્ધિ સાથે કેટલા પૈસા કમાવશો તેની ગણતરી કરી શકે છે.

સામાન્ય ચક્રવૃદ્ધિ વ્યાજ સૂત્ર

જ્યારે નાણાકીય સલાહકારો અસરનું વિશ્લેષણ કરે છે એક પર ચક્રવૃદ્ધિ વ્યાજરોકાણ, તેઓ સામાન્ય રીતે ત્રણ પરિબળોને ધ્યાનમાં લે છે જે રોકાણનું ભાવિ મૂલ્ય નક્કી કરે છે (FV):

• PV - રોકાણનું વર્તમાન મૂલ્ય
• i - દરેક સમયગાળામાં મેળવેલ વ્યાજ દર
• n - સમયગાળાની સંખ્યા

આ ઘટકોને જાણીને, તમે ચોક્કસ ચક્રવૃદ્ધિ વ્યાજ દર સાથે રોકાણનું ભવિષ્ય મૂલ્ય મેળવવા માટે નીચેના સૂત્રનો ઉપયોગ કરી શકો છો :

બિંદુને વધુ સારી રીતે સમજાવવા માટે, અહીં કેટલાક ઝડપી ઉદાહરણો છે.

ઉદાહરણ 1: માસિક ચક્રવૃદ્ધિ વ્યાજ સૂત્ર

ધારો કે, તમે માસિક ચક્રવૃદ્ધિ દરે 8% વ્યાજ દરે $2,000નું રોકાણ કરો છો અને તમે 5 વર્ષ પછી તમારા રોકાણનું મૂલ્ય જાણવા માગો છો.

પહેલાં, ચાલો તમારા ચક્રવૃદ્ધિ વ્યાજ સૂત્ર માટેના ઘટકોની સૂચિ લખીએ:<3

• PV = $2,000
• i = 8% પ્રતિ વર્ષ, ચક્રવૃદ્ધિ માસિક (0.08/12= 006666667)
• n = 5 વર્ષ x 12 મહિના (5*12= 60)

ઉપરોક્ત નંબરો ફોર્મ્યુલામાં દાખલ કરો, અને તમને મળશે:

= $2,000 * (1 + 0.8/12)5x12

અથવા

= $2,000 * 1.00666666760

અથવા

= $2,000 * 1.489845708 = $2,979.69 <3

ઉદાહરણ 2: દૈનિક ચક્રવૃદ્ધિ વ્યાજ સૂત્ર

મને આશા છે કે માસિક ચક્રવૃદ્ધિ વ્યાજનું ઉદાહરણ સારી રીતે સમજાયું છે, અને હવે તમે દૈનિક ચક્રવૃદ્ધિ માટે સમાન અભિગમનો ઉપયોગ કરી શકો છો. પ્રારંભિક રોકાણ, વ્યાજ દર, સમયગાળો અને ફોર્મ્યુલા ઉપરના ઉદાહરણની જેમ જ છે, માત્ર સંયોજન અવધિ અલગ છે:

• PV = $2,000
• i = 8% પ્રતિ વર્ષ, દૈનિક સંયોજન(0.08/365 = 0.000219178)
• n = 5 વર્ષ x 365 દિવસ (5*365 =1825)

ઉપરોક્ત નંબરોને ચક્રવૃદ્ધિ વ્યાજના સૂત્રમાં સપ્લાય કરો અને તમને મળશે નીચેનું પરિણામ:

=$2,000 * (1 + 0.000219178)1825 = $2,983.52

જેમ તમે જુઓ છો, દૈનિક ચક્રવૃદ્ધિ વ્યાજ સાથે, સમાન રોકાણનું ભાવિ મૂલ્ય માસિક ચક્રવૃદ્ધિ કરતાં થોડું વધારે છે. આ એટલા માટે છે કારણ કે 8% વ્યાજ દર દર મહિને બદલે દરરોજ મુખ્ય રકમમાં વ્યાજ ઉમેરે છે. જેમ તમે અનુમાન કરી શકો છો, માસિક ચક્રવૃદ્ધિ પરિણામ વાર્ષિક ચક્રવૃદ્ધિ કરતા વધારે હશે.

આ બધું સારું છે, પરંતુ તમને ખરેખર જોઈએ છે તે ચક્રવૃદ્ધિ વ્યાજ માટે એક્સેલ ફોર્મ્યુલા છે, ખરું ને? કૃપા કરીને થોડી વાર મારી સાથે સહન કરો. હવે અમે સૌથી રસપ્રદ ભાગ પર પહોંચી રહ્યા છીએ - એક્સેલમાં તમારું પોતાનું શક્તિશાળી અને બહુમુખી સંયોજન વ્યાજ કેલ્ક્યુલેટર બનાવવું.

એક્સેલમાં ચક્રવૃદ્ધિ વ્યાજ સૂત્ર (દૈનિક, સાપ્તાહિક, માસિક, વાર્ષિક ચક્રવૃદ્ધિ)

સામાન્ય રીતે , Excel માં કંઈક કરવા માટે એક કરતાં વધુ રીતો છે અને ચક્રવૃદ્ધિ વ્યાજ સૂત્ર એ અપવાદ નથી :) જો કે Microsoft Excel ચક્રવૃદ્ધિ વ્યાજની ગણતરી માટે કોઈ વિશેષ કાર્ય પ્રદાન કરતું નથી, તમે તમારા પોતાના સંયોજન વ્યાજ કેલ્ક્યુલેટર બનાવવા માટે અન્ય કાર્યોનો ઉપયોગ કરી શકો છો.

ચાલો એક્સેલ વર્કશીટમાં રોકાણના ભાવિ મૂલ્યને નિર્ધારિત કરતા મૂળભૂત પરિબળો દાખલ કરીને અમારા એક્સેલ સંયોજન વ્યાજ કેલ્ક્યુલેટર બનાવવાનું શરૂ કરીએ:

• પ્રારંભિક રોકાણ (B3)
• વાર્ષિક વ્યાજ દર(B4)
• દર વર્ષે સંયોજન સમયગાળાની સંખ્યા (B5)
• વર્ષોની સંખ્યા (B6)

જ્યારે પૂર્ણ થાય, ત્યારે તમારી એક્સેલ શીટ આના જેવી જ દેખાઈ શકે છે :

ઇનપુટ મૂલ્યોના આધારે કમાયેલી રકમ (બેલેન્સ)ની ગણતરી કરવા માટે હવે તમારે માત્ર સંયોજન વ્યાજ સૂત્રની જરૂર છે. શ્રેષ્ઠ સમાચાર એ છે કે તમારે વ્હીલની ફરીથી શોધ કરવાની જરૂર નથી. અમે બેંકિંગ અને અન્ય નાણાકીય સંસ્થાઓ દ્વારા ઉપયોગમાં લેવાતા સમય-ચકાસાયેલ ચક્રવૃદ્ધિ વ્યાજ સૂત્રને સરળ રીતે લઈશું અને તેનો એક્સેલની ભાષામાં અનુવાદ કરીશું.

એક્સેલ માટે ચક્રવૃદ્ધિ વ્યાજ સૂત્ર:

ઉપરોક્ત સ્ત્રોત ડેટા માટે, સૂત્ર આ આકાર લે છે:

=B3 * (1 + B4 /B5) ^ (B6 * B5)

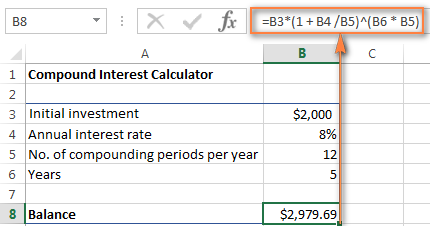
સંખ્યાઓ વધુ પરિચિત લાગે છે? હા, આ એ જ મૂલ્યો અને ગણતરીઓ છે જે અમે માસિક ચક્રવૃદ્ધિ વ્યાજ સૂત્ર સાથે કરી છે, અને પરિણામ એ સાબિત કરે છે કે અમે બધું બરાબર કર્યું છે!

જો તમે જાણવા માંગતા હોવ કે તમારું રોકાણ કેટલું મૂલ્યવાન થશે 8% વાર્ષિક વ્યાજ દર ચક્રવૃદ્ધિ ત્રિમાસિક , સેલ B5 માં ખાલી 4 દાખલ કરો:

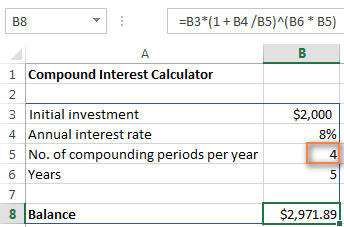
તમારા રોકાણના ભાવિ મૂલ્યની ગણતરી કરવા માટે સેમી -વાર્ષિક ચક્રવૃદ્ધિ, દર વર્ષે સંયોજન સમયગાળા મૂલ્ય તરીકે 2 દાખલ કરો. સાપ્તાહિક વ્યાજ દરો માટે, 52 દાખલ કરો, આ દર વર્ષે કેટલા અઠવાડિયા હોય છે. જો તમને રસ હોય તો દૈનિક કમ્પાઉન્ડિંગ, 365 દાખલ કરો, વગેરે.

કમાવેલ વ્યાજ ની રકમ શોધવા માટે, ફક્ત ભાવિ મૂલ્ય (બેલેન્સ) અને વર્તમાન વચ્ચેના તફાવતની ગણતરી કરો. મૂલ્ય (પ્રારંભિક રોકાણ). અમારા કિસ્સામાં, B9 માં સૂત્ર આટલું સરળ છે:

=B8-B3

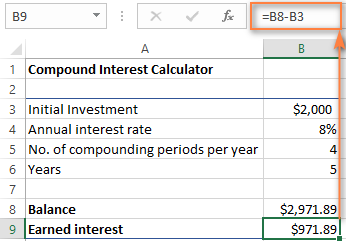
જેમ તમે જુઓ છો, અમે ખરેખર સાર્વત્રિક સંયોજન વ્યાજ કેલ્ક્યુલેટર બનાવ્યું છે એક્સેલ. આશા છે કે, હવે તમને કોઈ અફસોસ નથી કે તમે નાણાકીય આયોજકો દ્વારા ઉપયોગમાં લેવાતા જટિલ ચક્રવૃદ્ધિ વ્યાજના સૂત્રને શોધવામાં તમે થોડી કિંમતી મિનિટોનું રોકાણ કર્યું છે : )

એક્સેલ માટે એડવાન્સ્ડ સંયોજન વ્યાજ કેલ્ક્યુલેટર

જો કોઈ કારણોસર તમે ઉપરોક્ત અભિગમથી બિલકુલ ખુશ નથી, તમે એફવી ફંક્શનનો ઉપયોગ કરીને તમારું એક્સેલ કમ્પાઉન્ડ ઈન્ટરેસ્ટ કેલ્ક્યુલેટર બનાવી શકો છો જે એક્સેલ 2000 થી 2019ના તમામ વર્ઝનમાં ઉપલબ્ધ છે.

એફવી ફંક્શન રોકાણના ભાવિ મૂલ્યની ગણતરી કરે છે. અમે ચર્ચા કરી છે તેના જેવા જ ઇનપુટ ડેટાના આધારે, જો કે તેની વાક્યરચના થોડી અલગ છે:

દલીલોની વિગતવાર સમજૂતી એક્સેલ એફવી ફંક્શન ટ્યુટોરીયલમાં મળી શકે છે.

તે દરમિયાન, ચાલો માસિક ચક્રવૃદ્ધિ વ્યાજના ઉદાહરણની જેમ સમાન સ્રોત ડેટાનો ઉપયોગ કરીને FV ફોર્મ્યુલા બનાવીએ અને જોઈએ કે શું આપણને સમાન પરિણામ મળે છે.

તમને યાદ હશે તેમ, અમે 5 વર્ષ માટે $2,000 એક બચત ખાતામાં 8% માસિક ચક્રવૃદ્ધિ દરે જમા કરાવ્યા છે, કોઈ વધારાની ચૂકવણી વિના. તેથી, અમારા