টিউটোৰিয়েলত এক্সেলৰ বাবে চক্রবৃদ্ধি সুতৰ সূত্ৰটো ব্যাখ্যা কৰা হৈছে আৰু বাৰ্ষিক, মাহেকীয়া বা দৈনিক চক্রবৃদ্ধি সুতৰ হাৰত বিনিয়োগৰ ভৱিষ্যত মূল্য কেনেকৈ গণনা কৰিব পাৰি তাৰ উদাহৰণ দিয়া হৈছে। আপুনি আপোনাৰ নিজাকৈ E xcel কম্পাউণ্ড ইন্টাৰেষ্ট কেলকুলেটৰ তৈয়াৰ কৰাৰ বিশদ পদক্ষেপসমূহো পাব।

কম্পাউণ্ড ইন্টাৰেষ্ট বেংকিঙৰ অন্যতম মৌলিক বিল্ডিং ব্লক আৰু অন্যতম শক্তিশালী বিত্তীয়

যদিহে আপুনি এজন একাউণ্টিং স্নাতক, বিত্তীয় বিশ্লেষক বা অভিজ্ঞ বিনিয়োগকাৰী নহয়, তেন্তে বিশেষ বিত্তীয় বহী আৰু হাতপুথিৰ পৰা ধাৰণাটো ধৰি লোৱাটো অলপ কঠিন হ'ব পাৰে। এই লেখাটোৰ লক্ষ্য হৈছে ইয়াক সহজ কৰি তোলা : ) আপুনি এক্সেলত এটা চক্রবৃদ্ধি সুতৰ সূত্ৰ কেনেকৈ ব্যৱহাৰ কৰিব লাগে আৰু আপোনাৰ নিজৰ কাৰ্য্যপত্ৰিকাৰ বাবে এটা ইউনিভাৰ্চেল চক্রবৃদ্ধি সুতৰ কেলকুলেটৰ তৈয়াৰ কৰিব লাগে সেইটোও শিকিব।

কি চক্রবৃদ্ধি সুত নেকি?

অতি সহজ ভাষাত ক’বলৈ গ’লে চক্রবৃদ্ধি সুত হ’ল সুতৰ ওপৰত উপাৰ্জন কৰা সুত। অধিক নিখুঁতভাৱে ক’বলৈ গ’লে, প্ৰাৰম্ভিক জমা ধন (মূল) আৰু পূৰ্বৰ সময়ছোৱাৰ পৰা জমা হোৱা সুত দুয়োটাৰে চক্ৰ সুত আদায় কৰা হয়।

হয়তো, কেৱল মূলধনৰ পৰিমাণৰ ওপৰত গণনা কৰা সৰল সুতৰ পৰা আৰম্ভ কৰাটো সহজ হ’ব পাৰে। উদাহৰণস্বৰূপে, আপুনি বেংক একাউণ্টত ১০ ডলাৰ ৰাখে। ৭% বাৰ্ষিক সুতৰ হাৰত এবছৰৰ পিছত আপোনাৰ জমা ধনৰ মূল্য কিমান হ’ব? উত্তৰটো হ’ল ১০.৭০ ডলাৰ (১০ + ১০*০.০৭ =যৌগিক সুতৰ সূত্ৰটো তলত দিয়া ধৰণে:

=FV(0.08/12, 5*12, ,-2000)

যদি আপুনি প্ৰাচলসমূহৰ কিছু ব্যাখ্যাৰ প্ৰয়োজন হয়, ইয়াত আপুনি যাওক:

• হাৰ 0.008/12 যিহেতু আপুনি আছে 8% বাৰ্ষিক সুতৰ হাৰ মাহেকীয়া কম্পাউণ্ড।
• nper হৈছে 5*12, অৰ্থাৎ 5 বছৰ * 12 মাহ
• pmt খালী ৰখা হয় কাৰণ আমাৰ কোনো অতিৰিক্ত পেমেণ্ট নাই।
• pv -2000 কাৰণ ই এটা আউটফ্ল' আৰু ইয়াক এটা ঋণাত্মক সংখ্যাৰে প্ৰতিনিধিত্ব কৰা উচিত।

উপৰৰ সূত্ৰটো এটা খালী কোষত দিয়ক, আৰু ই ফলাফল হিচাপে $2,979.69 আউটপুট কৰিব (যিটো ৰ সৈতে নিখুঁতভাৱে ইনলাইন মাহেকীয়া যৌগিক সুতৰ উদাহৰণত কৰা গণিত গণনাৰ ফলাফল)।

স্বাভাৱিকভাৱে, একোৱেই আপোনাক মানসমূহ কোষ প্ৰসংগসমূহৰ সৈতে সলনি কৰাত বাধা নিদিয়ে:

=FV(B4/B5, B6*B5, , -B3)

তলৰ পৰ্দাশ্বটে দেখুৱাইছে ১৫ বছৰৰ পিছত ৪,০০০ ডলাৰ বিনিয়োগৰ ভৱিষ্যত মূল্য সাপ্তাহিকভাৱে ৭% কম্পাউণ্ড সুতৰ হাৰত:

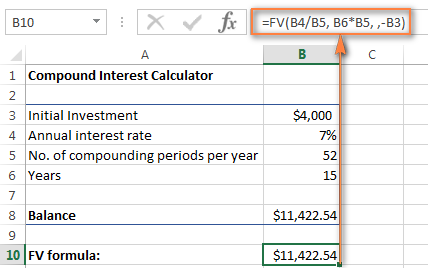
আপোনাৰ এক্সেল কম্পাউণ্ড সুতৰ কেলকুলেটৰক আৰু অধিক শক্তিশালী কৰিবলৈ, আপুনি ইয়াক বৃদ্ধি কৰিব পাৰে অতিৰিক্ত অৱদানসমূহ বিকল্পৰ সৈতে n (অতিৰিক্ত পেমেণ্ট) আৰু সেই অনুসৰি চক্রবৃদ্ধি সুতৰ সূত্ৰটো পৰিৱৰ্তন কৰা।

=FV(B4/B5, B6*B5, -B8, -B3, B9)

ক'ত:

• B3 - মূলধন বিনিয়োগ
• B4 - বাৰ্ষিক সুতৰ হাৰ
• B5 - প্ৰতি বছৰে কম্পাউণ্ডিং পিৰিয়ডৰ সংখ্যা
• B6 - সঞ্চয় কৰিবলগীয়া বছৰৰ সংখ্যা
• B8 - অতিৰিক্ত অৱদান (ঐচ্ছিক)
• B9 - অতিৰিক্ত অৱদানৰ ধৰণ। মনত ৰাখিব যে আপুনি এটা জমা কৰিলে ১ লিখকযৌগিক সময়ছোৱাৰ আৰম্ভণিতে অতিৰিক্ত ধনৰাশি, 0 বা সময়সীমাৰ শেষত অতিৰিক্ত ধন পৰিশোধ কৰিলে বাদ দিয়া হয়।

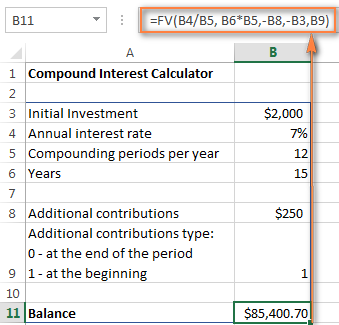
যদি আপুনি এইটো চেষ্টা কৰিবলৈ কৌতুহলী আপোনাৰ সঞ্চয় গণনা কৰিবলৈ এক্সেলৰ বাবে উন্নত কম্পাউণ্ড ইন্টাৰেষ্ট কেলকুলেটৰ, আপুনি ইয়াক এই পোষ্টৰ শেষত ডাউনলোড কৰিব পাৰে।

টিপচ্। চক্রবৃদ্ধি সুত গণনা কৰাৰ আন এটা দ্ৰুত উপায় হ’ল এক্সেল ডাটা টেবুলৰ সহায়ত What-If বিশ্লেষণ কৰা।

অনলাইনত যৌগিক সুত গণনাকাৰী

যদি আপুনি কেনেকৈ সেইটো বুজিবলৈ সময়তকৈ ধন বিনিয়োগ কৰাটো পছন্দ কৰে এক্সেলত চক্রবৃদ্ধি সুত গণনা কৰিবলৈ অনলাইন চক্রবৃদ্ধি সুত কেলকুলেটৰ কামত আহিব পাৰে। আপোনাৰ পছন্দৰ চাৰ্চ ইঞ্জিনত "কম্পাউণ্ড ইন্টাৰেষ্ট কেলকুলেটৰ"ৰ দৰে কিবা এটা লিখি আপুনি ইয়াৰ প্ৰচুৰ পৰিমাণে বিচাৰি পাব পাৰে। ইয়াৰ মাজতে মোৰ প্ৰিয় দুটামান ক্ষন্তেকতে উপস্থাপন কৰিম।

বেংকৰেটৰ দ্বাৰা কম্পাউণ্ড ইন্টাৰেষ্ট কেলকুলেটৰ

বেংকৰেট কম্পাউণ্ড ইন্টাৰেষ্ট কেলকুলেটৰৰ মূল সুবিধাসমূহ হ'ল ব্যৱহাৰৰ সহজতা আৰু দৃশ্যমান উপস্থাপন ফলাফলবোৰ. এই কেলকুলেটৰে আপোনাক সঞ্চয় ইনপুটসমূহ বাকচসমূহত বা এটা স্লাইডাৰ স্থানান্তৰ কৰি হস্তচালিতভাৱে সুমুৱাবলৈ দিয়ে। আপুনি এইটো কৰাৰ সময়ত, আনুমানিক মুঠ ওপৰত প্ৰদৰ্শিত হয় আৰু তৎক্ষণাত তলৰ গ্ৰাফত প্ৰতিফলিত হয়:

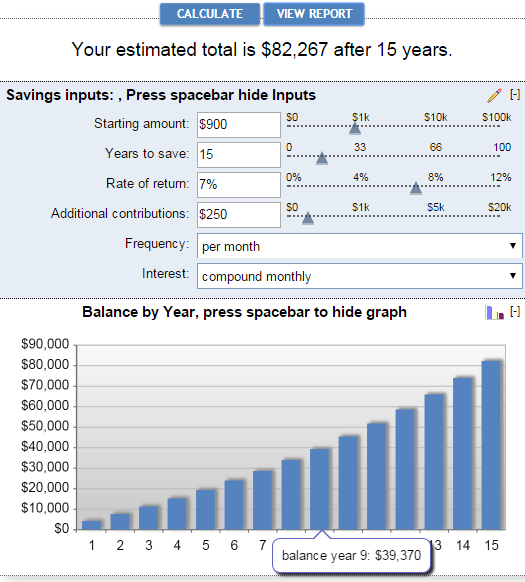
ৰিপৰ্ট চাওক বুটাম ক্লিক কৰিলে এটা "সাৰাংশ" সৃষ্টি হয় প্ৰতিবেদন"ৰ লগতে "সঞ্চয় বেলেঞ্চ" যিয়ে অতিৰিক্ত অৱদানৰ পৰিমাণ, উপাৰ্জিত সুত আৰু বেলেঞ্চৰ বিশদ তথ্য প্ৰদান কৰেপ্ৰতি বছৰৰ বাবে।

মানি-জাইনৰ দ্বাৰা যৌগিক সুতৰ কেলকুলেটৰ

মানি-জাইনৰ পৰা অনলাইন কেলকুলেটৰটো বেংকৰেটৰ তুলনাত বহুত সহজ। ই আপোনাক মাত্ৰ ৩টা মূল্য নিৰ্দিষ্ট কৰিবলৈ কয়: মূল বিনিয়োগ, সুতৰ হাৰ আৰু সময়সীমা। আপুনি এই সংখ্যাসমূহ যোগান ধৰাৰ লগে লগে আৰু গণনা বুটাম ক্লিক কৰাৰ লগে লগে, ই আপোনাক সকলো ধৰণৰ চক্রবৃদ্ধি সুতৰ হাৰ (দৈনিক, সাপ্তাহিক, মাহেকীয়া, বাৰ্ষিক, ইত্যাদি) আৰু লগতে ভৱিষ্যতৰ মানসমূহ এটা সংশ্লিষ্টৰ সৈতে দেখুৱাব compounding.

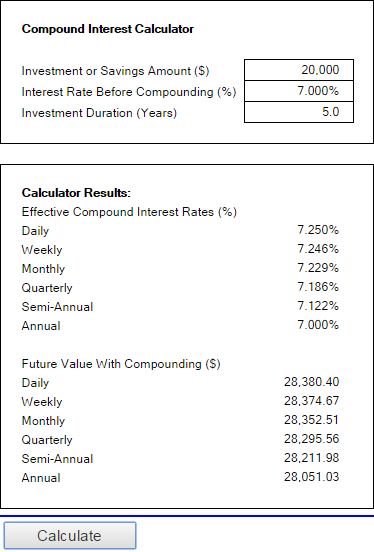
MoneySmart দ্বাৰা কম্পাউণ্ড সুতৰ কেলকুলেটৰ

এইটো অষ্ট্ৰেলিয়ান ছিকিউৰিটিজ এণ্ড ইনভেষ্টমেণ্টছ কমিছনে চলোৱা এটা সঁচাকৈয়ে ভাল অনলাইন কম্পাউণ্ড ইন্টাৰেষ্ট কেলকুলেটৰ। ই আপোনাক সকলো প্ৰাসংগিক কাৰক ইনপুট কৰিবলৈ দিয়ে যিয়ে আপোনাৰ বিনিয়োগৰ ভৱিষ্যত মূল্য নিৰ্ধাৰণ কৰে আৰু ফলাফলটো এটা গ্ৰাফ হিচাপে আউটপুট কৰে। গ্ৰাফত এটা নিৰ্দিষ্ট বাৰৰ ওপৰত হুভাৰ কৰি, আপুনি সেই বিশেষ বছৰৰ বাবে সাৰাংশ তথ্য চাব পাৰিব।

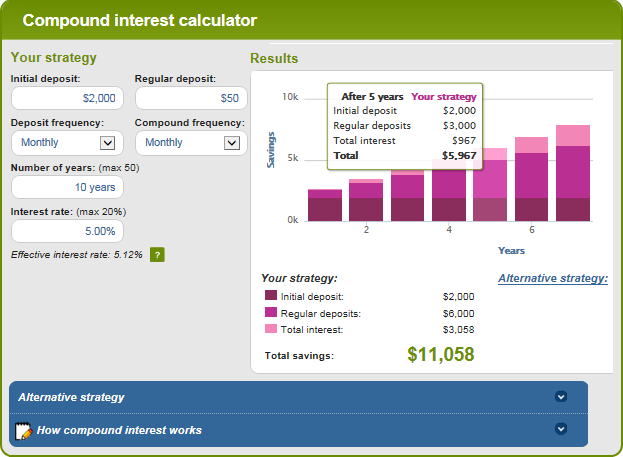
আপুনি এক্সেল আৰু ইয়াৰ বাহিৰত চক্রবৃদ্ধি সুত কেনেকৈ গণনা কৰে :) আশাকৰোঁ এই লেখাটোত আলোচনা কৰা অন্ততঃ এটা যৌগিক সুতৰ সূত্ৰ আপোনালোকৰ বাবে সহায়ক বুলি প্ৰমাণিত হৈছে। যিয়েই নহওক, মই আপোনাক পঢ়াৰ বাবে ধন্যবাদ জনাইছো আৰু অহা সপ্তাহত আমাৰ ব্লগত আপোনাক লগ পাম বুলি আশা কৰিছো!

ডাউনল'ডৰ বাবে অনুশীলন কাৰ্য্যপুস্তিকা

এক্সেলৰ বাবে যৌগিক আগ্ৰহ কেলকুলেটৰ (.xlsx ফাইল)

যৌগিক সুত ৰ ক্ষেত্ৰত, প্ৰতিটো সময়সীমাৰ মূলধন বেলেগ বেলেগ। বেংকে উপাৰ্জিত সুত আপোনাক ঘূৰাই নিদিয়ে, বৰঞ্চ আপোনাৰ মূল বিনিয়োগত যোগ কৰে। এই বৃদ্ধি পোৱা ধনৰাশি পৰৱৰ্তী সময়ৰ বাবে (যৌগিক সময়ছোৱা) মূলধন হৈ পৰে আৰু সুতও আদায় কৰে। অৰ্থাৎ, আপুনি কেৱল মূলধনৰ ধনৰ ওপৰত নহয়, প্ৰতিটো কম্পাউণ্ডিং পিৰিয়ডত উপাৰ্জিত সুতৰ ওপৰতো সুত আদায় কৰে।

আমাৰ উদাহৰণত, ১০ ডলাৰৰ মূলধনৰ উপৰিও ০.৭০ ডলাৰৰ উপাৰ্জিত সুত হ’ব অহা বছৰো সুত আদায় কৰিব। গতিকে, বছৰি ৭% কম্পাউণ্ড বাৰ্ষিক সুতৰ হাৰত ২ বছৰৰ পিছত আপোনাৰ ১০ ডলাৰ জমা ধনৰ মূল্য কিমান হ’ব? উত্তৰটো হ’ল ১১.৪৫ ডলাৰ (১০.৭ + ১০.৭*০.০৭ = ১১.৪৫) আৰু আপোনাৰ <৯>আৰ্জিত সুত<১০> ১.৪৫ ডলাৰ। আপুনি দেখিছে যে দ্বিতীয় বছৰৰ শেষত আপুনি কেৱল প্ৰাৰম্ভিক ১০ ডলাৰ জমা ধনত ০.৭০ ডলাৰ উপাৰ্জন কৰাই নহয়, প্ৰথম বছৰত জমা হোৱা ০.৭০ ডলাৰৰ সুতৰ ওপৰতো ০.০৫ ডলাৰ উপাৰ্জন কৰিছিল।

এক্সেলত চক্রবৃদ্ধি সুত গণনা কৰাৰ কেইবাটাও উপায় আছে, আৰু আমি প্ৰতিটোৰ বিষয়ে বিতংভাৱে আলোচনা কৰিম।

এক্সেলত চক্রবৃদ্ধি সুত কেনেকৈ গণনা কৰিব পাৰি

দীঘলীয়া সময়ৰ বিনিয়োগ আপোনাৰ সম্পদ বৃদ্ধিৰ বাবে এক ফলপ্ৰসূ কৌশল হ'ব পাৰে, আৰু আনকি সৰু সৰু জমা ধনেও সময়ৰ লগে লগে ডাঙৰ পৰিৱৰ্তন আনিব পাৰে। অধিক ব্যাখ্যা কৰা এক্সেলৰ যৌগিক সুতৰ সূত্ৰসমূহে আপোনাক সঞ্চয় কৌশলটো লাভ কৰাত সহায় কৰিবকাম. অৱশেষত আমি এটা সাৰ্বজনীন সূত্ৰ তৈয়াৰ কৰিবলৈ ওলাইছো যিয়ে বিভিন্ন যৌগিক সময়ৰ সৈতে ভৱিষ্যতৰ মূল্য গণনা কৰে - দৈনিক, সাপ্তাহিক, মাহেকীয়া, ত্ৰিমাসিক, বা বছৰেকীয়া।

এক্সেলত বাৰ্ষিক যৌগিক সুত গণনা কৰা

To এই টিউটোৰিয়েলৰ আৰম্ভণিতে আলোচনা কৰা এটা অতি সহজ উদাহৰণৰ পৰা আৰম্ভ কৰোঁ আৰু এক্সেলত বাৰ্ষিক যৌগিক সুত গণনা কৰিবলৈ এটা সূত্ৰ লিখা যাওক। আপুনি মনত পেলোৱা মতে, আপুনি ৭% বাৰ্ষিক সুতৰ হাৰত ১০ ডলাৰ বিনিয়োগ কৰিছে আৰু বছৰেকীয়া কম্পাউণ্ডিঙে আপোনাৰ সঞ্চয় কেনেকৈ বৃদ্ধি কৰে সেয়া জানিব বিচাৰিছে।

বাৰ্ষিক চক্রবৃদ্ধি সুত - সূত্ৰ ১

এটা সহজ আৰু পোনপটীয়া উপায় বাৰ্ষিক যৌগিক সুতৰ সৈতে উপাৰ্জিত ধনৰাশি গণনা কৰিবলৈ এটা সংখ্যা শতাংশ বৃদ্ধি কৰিবলৈ সূত্ৰটো ব্যৱহাৰ কৰা হৈছে:

=Amount * (1 + %) ।

আমাৰ উদাহৰণত, সূত্ৰটো হ'ল:

=A2*(1+$B2)

য'ত A2 হৈছে আপোনাৰ প্ৰাৰম্ভিক জমা ধন আৰু B2 হৈছে বাৰ্ষিক সুতৰ হাৰ। অনুগ্ৰহ কৰি মন কৰক যে আমি $ চিহ্ন ব্যৱহাৰ কৰি B স্তম্ভৰ উল্লেখটো ঠিক কৰি দিওঁ।

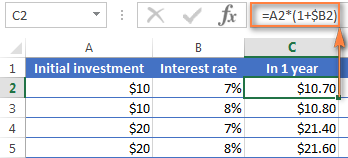
আপুনি মনত ৰখাৰ দৰে, 1% এশৰ এটা অংশ, অৰ্থাৎ 0.01, গতিকে 7 % হৈছে 0.07, আৰু এইদৰে শতাংশসমূহ প্ৰকৃততে Excel ত সংৰক্ষণ কৰা হয়। এই কথা মনত ৰাখি, আপুনি 10*(1+0.07) বা 10*1.07 ৰ এটা সৰল গণনা কৰি সূত্ৰটোৱে ঘূৰাই দিয়া ফলাফল পৰীক্ষা কৰিব পাৰে আৰু নিশ্চিত কৰিব পাৰে যে 1 বছৰৰ পিছত আপোনাৰ বেলেঞ্চ সঁচাকৈয়ে $10.70 হ'ব।

আৰু এতিয়া, ২ বছৰৰ পিছত বেলেঞ্চ গণনা কৰা যাওক। গতিকে, কেনেকৈআপোনাৰ ১০ ডলাৰ জমা ধনৰ মূল্য দুবছৰৰ ভিতৰত ৭% বাৰ্ষিক সুতৰ হাৰত কিমান হ'ব? উত্তৰটো হ'ল $11.45 আৰু আপুনি একেটা সূত্ৰ D স্তম্ভত কপি কৰি পাব পাৰে।

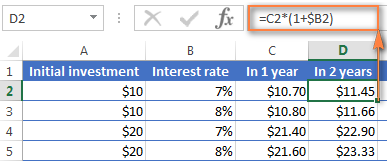
৩ ৰ শেষত আপুনি আপোনাৰ বেংক একাউণ্টত কিমান টকা পাব সেইটো গণনা কৰিবলৈ বছৰ বছৰ ধৰি, কেৱল একেটা সূত্ৰক E স্তম্ভত কপি কৰক আৰু আপুনি $12.25 পাব।

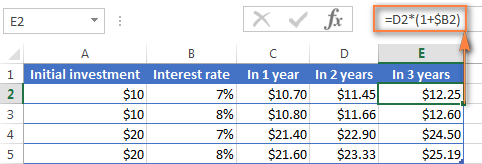
আপোনালোকৰ যিসকলৰ Excel সূত্ৰৰ কিছু অভিজ্ঞতা আছে তেওঁলোকে হয়তো বুজি পাইছে যে ওপৰৰ সূত্ৰটো কি প্ৰকৃততে $10 ৰ প্ৰাৰম্ভিক জমা ধনক 1.07 ৰে তিনিবাৰ গুণ কৰা:

=10*1.07*1.07*1.07=12.25043

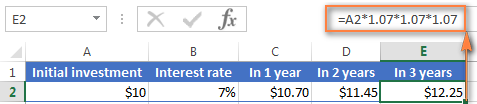
ইয়াক দুটা দশমিক স্থানলৈ ঘূৰাই দিয়ক আৰু আপুনি ওপৰৰ স্ক্ৰীণশ্বটত E2 কোষত দেখাৰ দৰে একে সংখ্যা পাব - ১২.২৫ ডলাৰ। স্বাভাৱিকতে এই সূত্ৰটো ব্যৱহাৰ কৰি ৩ বছৰৰ পিছত বেলেঞ্চ পোনপটীয়াকৈ গণনা কৰিব পাৰি:

=A2*1.07*1.07*1.07

বাৰ্ষিক চক্রবৃদ্ধি সুত - সূত্ৰ ২

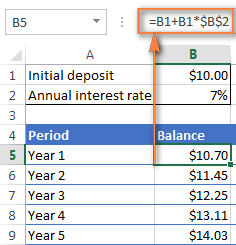
আন এটা বাৰ্ষিক চক্রবৃদ্ধি সুতৰ সূত্ৰ এটা বনোৱাৰ উপায় হ'ল প্ৰতিটো বছৰৰ বাবে উপাৰ্জিত সুত গণনা কৰা আৰু তাৰ পিছত ইয়াক প্ৰাৰম্ভিক জমা ধনত যোগ কৰা>B2 কোষত বাৰ্ষিক সুতৰ হাৰ , তলত দিয়া সূত্ৰটোৱে এটা ট্ৰিট কাম কৰে:

=B1 + B1 * $B$2

সূত্ৰটোৱে সঠিকভাৱে কাম কৰিবলৈ, অনুগ্ৰহ কৰি মন কৰক নিম্নলিখিত বিৱৰণ:

• $ চিহ্ন যোগ কৰি বাৰ্ষিক সুতৰ হাৰ কোষ (আমাৰ ক্ষেত্ৰত B2) ৰ উল্লেখ ঠিক কৰক, ই এটা নিৰপেক্ষ স্তম্ভ আৰু নিৰপেক্ষ শাৰী হ'ব লাগে, যেনে $B$2.
• ২য় বছৰৰ বাবে (B6)আৰু পৰৱৰ্তী সকলো বছৰ, সূত্ৰটো সলনি কৰক:

  বছৰ ১ বেলেঞ্চ + বছৰ ১ বেলেঞ্চ * সুতৰ হাৰ

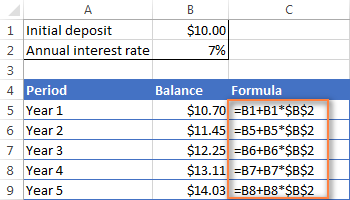
এই উদাহৰণত, আপুনি নিম্নলিখিত সূত্ৰটো কোষ B6 আৰু... তাৰ পিছত ইয়াক অন্য শাৰীলৈ কপি কৰক, যেনে তলৰ স্ক্ৰীণশ্বটত দেখুওৱা হৈছে:

=B5 + B5 * $B$2

আপুনি বাৰ্ষিক কম্পাউণ্ডিঙৰ দ্বাৰা প্ৰকৃততে কিমান সুত উপাৰ্জন কৰিলে সেয়া জানিবলৈ, ১ বছৰৰ পিছৰ ভাৰসাম্য (B5) ৰ পৰা প্ৰাথমিক জমা (B1) বিয়োগ কৰক। এই সূত্ৰটো C5 লৈ যায়:

=B5-B1

C6 ত, 2 বছৰৰ পিছত ভাৰসাম্য ৰ পৰা ১ বছৰৰ পিছত ভাৰসাম্য বিয়োগ কৰক, আৰু সূত্ৰটো তললৈ টানি নিয়ক অন্য কোষলৈ:

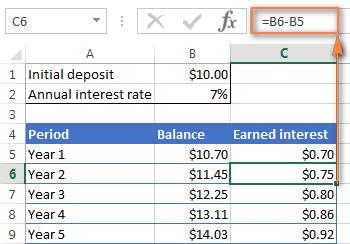
=B6-B5

আপুনি তলৰ স্ক্ৰীণশ্বটৰ দৰে আৰ্জিত আগ্ৰহ বৃদ্ধি চাব লাগে।

ওপৰৰ উদাহৰণবোৰে চক্রবৃদ্ধি সুতৰ ধাৰণাটোক চিত্ৰিত কৰি ভাল কাম কৰিছে নহয়নে? কিন্তু কোনো এটা সূত্ৰই এক্সেলৰ বাবে ইউনিভাৰ্চেল কম্পাউণ্ড ইন্টাৰেষ্ট সূত্ৰ বুলি ক’ব পৰাকৈ ভাল নহয়। প্ৰথমতে, কাৰণ তেওঁলোকে আপোনাক এটা কম্পাউণ্ডিং ফ্ৰিকুৱেন্সি নিৰ্দিষ্ট কৰিবলৈ নিদিয়ে, আৰু দ্বিতীয়তে, কাৰণ আপুনি কেৱল এটা নিৰ্দিষ্ট সময়সীমা আৰু সুতৰ হাৰ প্ৰৱেশ নকৰি এটা সম্পূৰ্ণ টেবুল নিৰ্মাণ কৰিব লাগিব।

বাৰু, আহক আমি এখোজ আগুৱাই গৈ সৃষ্টি কৰোঁ এক্সেলৰ বাবে এটা সাৰ্বজনীন চক্রবৃদ্ধি সুতৰ সূত্ৰ যিয়ে বছৰেকীয়া, ত্ৰিমাসিক, মাহেকীয়া, সাপ্তাহিক বা দৈনিক কম্পাউণ্ডিঙৰ দ্বাৰা আপুনি কিমান ধন উপাৰ্জন কৰিব সেইটো গণনা কৰিব পাৰে।

সাধাৰণ চক্ৰীয় সুতৰ সূত্ৰ

যেতিয়া বিত্তীয় উপদেষ্টাসকলে প্ৰভাৱ বিশ্লেষণ কৰে যৌগিক সুতৰ ওপৰত anবিনিয়োগ, তেওঁলোকে সাধাৰণতে বিনিয়োগৰ ভৱিষ্যত মূল্য (FV) নিৰ্ধাৰণ কৰা তিনিটা কাৰক বিবেচনা কৰে:

• PV - বিনিয়োগৰ বৰ্তমান মূল্য
• i - প্ৰতিটো সময়ছোৱাত উপাৰ্জিত সুতৰ হাৰ
• n - সময়ৰ সংখ্যা

এই উপাদানসমূহ জানিলে আপুনি তলৰ সূত্ৰটো ব্যৱহাৰ কৰি এটা নিৰ্দিষ্ট চক্ৰীয় সুতৰ হাৰৰ সৈতে বিনিয়োগৰ ভৱিষ্যতৰ মূল্য পাব পাৰে :

বিন্দুটো ভালদৰে বুজাবলৈ দুটামান দ্ৰুত উদাহৰণ দিয়া হ'ল।

উদাহৰণ ১: মাহেকীয়া যৌগিক সুতৰ সূত্ৰ

ধৰি লওক, আপুনি মাহেকীয়াকৈ ৮% সুতৰ হাৰত ২,০০০ ডলাৰ বিনিয়োগ কৰে আৰু আপুনি ৫ বছৰৰ পিছত আপোনাৰ বিনিয়োগৰ মূল্য জানিব বিচাৰে।

প্ৰথমে, আপোনাৰ চক্রবৃদ্ধি সুতৰ সূত্ৰৰ বাবে উপাদানসমূহৰ তালিকা এখন লিখি থওঁ:

• PV = $2,000
• i = প্ৰতি বছৰে 8%, মাহেকীয়া যৌগিক (0.08/12= 006666667)
• n = 5 বছৰ x 12 মাহ (5*12= ৬০)

সূত্ৰত ওপৰৰ সংখ্যাবোৰ ইনপুট কৰক, আৰু আপুনি পাব:

= $2,000 * (1 + 0.8/12)5x12

বা

= $2,000 * 1.00666666760

বা

২৭৩১<৩>

উদাহৰণ ২: দৈনিক যৌগিক সুতৰ সূত্ৰ

মই আশা কৰোঁ মাহেকীয়া চক্রবৃদ্ধি সুতৰ উদাহৰণটো ভালদৰে বুজা হৈছে, আৰু এতিয়া আপুনি দৈনিক যৌগিক সুতৰ বাবে একে পদ্ধতি ব্যৱহাৰ কৰিব পাৰিব। প্ৰাৰম্ভিক বিনিয়োগ, সুতৰ হাৰ, সময়সীমা আৰু সূত্ৰটো ওপৰৰ উদাহৰণটোৰ দৰেই, কেৱল কম্পাউণ্ডিং সময়ছোৱাই বেলেগ:

• PV = $2,000
• i = 8% প্ৰতি বছৰে, দৈনিক যৌগিক(০.০৮/৩৬৫ = ০.০০০২১৯১৭৮)<২১><২০>n = ৫ বছৰ x ৩৬৫ দিন (৫*৩৬৫ =১৮২৫)

উপৰোক্ত সংখ্যাবোৰ যৌগিক সুতৰ সূত্ৰত যোগান ধৰিব, আৰু আপুনি পাব তলত দিয়া ফলাফল:

=$2,000 * (1 + 0.000219178)1825 = $2,983.52

আপুনি দেখাৰ দৰে, দৈনিক কম্পাউণ্ডিং সুতৰ সৈতে, একেটা বিনিয়োগৰ ভৱিষ্যত মূল্য মাহেকীয়া কম্পাউণ্ডিংতকৈ অলপ বেছি। কাৰণ ৮% সুতৰ হাৰে প্ৰতিমাহে নহয়, প্ৰতিদিনে মূলধনৰ ধনৰ ওপৰত সুত যোগ কৰে। আপুনি অনুমান কৰিব পাৰে যে মাহেকীয়া কম্পাউণ্ডিঙৰ ফলাফল বাৰ্ষিক কম্পাউণ্ডতকৈ বেছি হ’ব।

এই সকলোবোৰ ভাল, কিন্তু আপুনি প্ৰকৃততে যিটো বিচাৰে সেয়া হ’ল কম্পাউণ্ড সুতৰ বাবে এক্সেল সূত্ৰ, নহয়নে? মাত্ৰ আৰু অলপ সময় মোক সহ্য কৰক, অনুগ্ৰহ কৰি। এতিয়া আমি আটাইতকৈ আকৰ্ষণীয় অংশটোলৈ আহিছো - এক্সেলত নিজৰ শক্তিশালী আৰু বহুমুখী কম্পাউণ্ড ইন্টাৰেষ্ট কেলকুলেটৰ নিৰ্মাণ কৰা।

এক্সেলত কম্পাউণ্ড ইন্টাৰেষ্ট সূত্ৰ (দৈনিক, সাপ্তাহিক, মাহেকীয়া, বছৰেকীয়া কম্পাউণ্ডিং)

সাধাৰণতে , Excel ত কিবা এটা কৰাৰ এটাতকৈ অধিক উপায় আছে আৰু এটা চক্রবৃদ্ধি সুতৰ সূত্ৰ ইয়াৰ ব্যতিক্ৰম নহয় :) যদিও Microsoft Excel এ চক্রবৃদ্ধি সুত গণনাৰ বাবে কোনো বিশেষ ফাংচন প্ৰদান নকৰে, আপুনি আপোনাৰ নিজৰ চক্রবৃদ্ধি সুতৰ কেলকুলেটৰ সৃষ্টি কৰিবলৈ অন্য ফাংচন ব্যৱহাৰ কৰিব পাৰে।<3 | বাৰ্ষিক সুতৰ হাৰ(B4)

যেতিয়া সম্পূৰ্ণ হয়, আপোনাৰ এক্সেল শ্বীটটো ইয়াৰ দৰেই দেখা যাব পাৰে :

এতিয়া আপুনি প্ৰয়োজন মাথোঁ ইনপুট মূল্যৰ ওপৰত ভিত্তি কৰি উপাৰ্জিত পৰিমাণ (বেলেন্স) গণনা কৰিবলৈ চক্রবৃদ্ধি সুতৰ সূত্ৰ। আটাইতকৈ ভাল খবৰটো হ’ল চকাটো পুনৰ উদ্ভাৱন কৰিব নালাগে। আমি কেৱল বেংকিং আৰু অন্যান্য বিত্তীয় প্ৰতিষ্ঠানে ব্যৱহাৰ কৰা সময় পৰীক্ষা কৰা চক্রবৃদ্ধি সুতৰ সূত্ৰটো লৈ এক্সেলৰ ভাষালৈ অনুবাদ কৰিম।

এক্সেলৰ বাবে যৌগিক সুতৰ সূত্ৰ:

ওপৰৰ উৎস তথ্যৰ বাবে সূত্ৰটোৱে এই আকৃতি লয়:

=B3 * (1 + B4 /B5) ^ (B6 * B5)

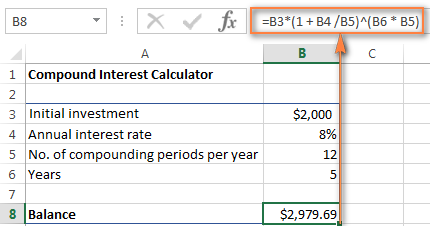
সংখ্যাবোৰ যথেষ্ট চিনাকি যেন লাগে? হ'ব, এইবোৰ আমি মাহেকীয়া চক্রবৃদ্ধি সুতৰ সূত্ৰৰ সৈতে কৰা একেবোৰ মূল্য আৰু গণনা, আৰু ফলাফলে প্ৰমাণ কৰে যে আমি সকলো ঠিকেই কৰিলোঁ!

যদি আপুনি জানিব বিচাৰে যে আপোনাৰ বিনিয়োগৰ মূল্য কিমান হ'ব 8% বাৰ্ষিক সুতৰ হাৰ যৌগিক ত্ৰিমাসিক , কেৱল B5 কোষত 4 লিখক:

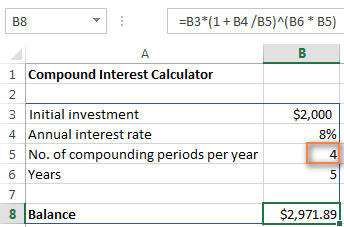
আপোনাৰ বিনিয়োগৰ ভৱিষ্যত মূল্য ছেমিৰ সৈতে গণনা কৰিবলৈ -বাৰ্ষিক কম্পাউণ্ডিং, প্ৰতি বছৰত কম্পাউণ্ডিং পিৰিয়ডসমূহ মান হিচাপে 2 লিখক। সাপ্তাহিক সুতৰ হাৰৰ বাবে 52 লিখক, এইটোৱেই হ'ল প্ৰতি বছৰে কিমান সপ্তাহ থাকে। যদি আপুনি আগ্ৰহী দৈনিক কম্পাউণ্ডিং, 365 লিখক, ইত্যাদি।

আৰ্জিত সুতৰ পৰিমাণ বিচাৰিবলৈ, কেৱল ভৱিষ্যতৰ মূল্য (ভাৰসাম্য) আৰু বৰ্তমানৰ মাজৰ পাৰ্থক্য গণনা কৰক মূল্য (প্ৰাথমিক বিনিয়োগ)। আমাৰ ক্ষেত্ৰত, B9 ত সূত্ৰটো ইমানেই সহজ যেনে:

=B8-B3

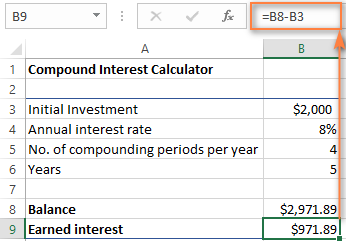
আপুনি দেখাৰ দৰে, আমি ইয়াৰ বাবে এটা সঁচাকৈয়ে সাৰ্বজনীন চক্ৰীয় সুতৰ কেলকুলেটৰ তৈয়াৰ কৰিছো এক্সেল। আশাকৰোঁ, এতিয়া আপুনি কোনো আক্ষেপ নাই যে আপুনি বিত্তীয় পৰিকল্পনাকাৰীসকলে ব্যৱহাৰ কৰা কৌশলী চক্রবৃদ্ধি সুতৰ সূত্ৰটো উলিয়াবলৈ কেইটামান বহুমূলীয়া মিনিট বিনিয়োগ কৰিলে : )

এক্সেলৰ বাবে উন্নত চক্রবৃদ্ধি সুতৰ কেলকুলেটৰ

যদি কিবা কাৰণত হয় আপুনি ওপৰৰ পদ্ধতিত একেবাৰে সুখী নহয়, আপুনি আপোনাৰ Excel কম্পাউণ্ড সুতৰ কেলকুলেটৰ সৃষ্টি কৰিব পাৰে FV ফাংচন ব্যৱহাৰ কৰি যি Excel 2000 ৰ পৰা 2019 লৈকে সকলো সংস্কৰণত উপলব্ধ।

FV ফাংচনে এটা বিনিয়োগৰ ভৱিষ্যত মূল্য গণনা কৰে আমি আলোচনা কৰা ইনপুট ডাটাৰ ওপৰত ভিত্তি কৰি, যদিও ইয়াৰ বাক্যবিন্যাস অলপ বেলেগ:

আৰ্গুমেণ্টৰ বিশদ ব্যাখ্যা ইয়াৰ মাজতে, মাহেকীয়া যৌগিক সুতৰ উদাহৰণৰ দৰে একেটা উৎস তথ্য ব্যৱহাৰ কৰি এটা FV সূত্ৰ নিৰ্মাণ কৰোঁ আৰু চাওঁ যে আমি একে ফলাফল পাম নেকি।

আপুনি মনত আছে যে আমি ৫ বছৰৰ বাবে ২০০০ ডলাৰ মাহেকীয়াকৈ ৮% বাৰ্ষিক সুতৰ হাৰত কম্পাউণ্ড কৰি চেভিংছ একাউণ্টত জমা কৰিলোঁ, কোনো অতিৰিক্ত ধন পৰিশোধ নকৰাকৈ। গতিকে, আমাৰ...