টিউটোরিয়ালটি এক্সেলের জন্য চক্রবৃদ্ধি সুদের সূত্র ব্যাখ্যা করে এবং কীভাবে বার্ষিক, মাসিক বা দৈনিক চক্রবৃদ্ধি সুদের হারে বিনিয়োগের ভবিষ্যতের মূল্য গণনা করতে হয় তার উদাহরণ প্রদান করে। এছাড়াও আপনি আপনার নিজস্ব E xcel চক্রবৃদ্ধি সুদের ক্যালকুলেটর তৈরি করার বিশদ ধাপগুলিও পাবেন৷

চক্রীকরণ সুদ হল ব্যাঙ্কিং-এর অন্যতম মৌলিক বিল্ডিং ব্লক এবং সবচেয়ে শক্তিশালী আর্থিক ব্যবস্থাগুলির মধ্যে একটি৷ এর চারপাশের শক্তিগুলি আপনার বিনিয়োগের ফলাফল নির্ধারণ করে৷

যদি না আপনি একজন অ্যাকাউন্টিং স্নাতক, আর্থিক বিশ্লেষক বা একজন অভিজ্ঞ বিনিয়োগকারী না হন, বিশেষায়িত আর্থিক বই এবং ম্যানুয়াল থেকে ধারণাটি উপলব্ধি করা কিছুটা কঠিন হতে পারে৷ এই নিবন্ধটির উদ্দেশ্য হল এটিকে সহজ করা : ) আপনি এক্সেলে কীভাবে একটি চক্রবৃদ্ধি সুদের সূত্র ব্যবহার করবেন এবং আপনার নিজস্ব ওয়ার্কশীটের জন্য একটি সর্বজনীন যৌগিক সুদের ক্যালকুলেটর তৈরি করবেন তাও শিখবেন৷

কী চক্রবৃদ্ধি সুদ কি?

খুব সহজ ভাষায়, চক্রবৃদ্ধি সুদ হল সুদের উপর অর্জিত সুদ। আরও স্পষ্টভাবে বলতে গেলে, প্রাথমিক আমানত (মূল) এবং পূর্ববর্তী মেয়াদ থেকে সংগৃহীত সুদ উভয়ের উপরই চক্রবৃদ্ধি সুদ অর্জিত হয়।

সম্ভবত, সাধারণ সুদের সাথে শুরু করা সহজ হতে পারে যা শুধুমাত্র মূল পরিমাণে গণনা করা হয়। উদাহরণস্বরূপ, আপনি একটি ব্যাঙ্ক অ্যাকাউন্টে $10 রাখেন। 7% বার্ষিক সুদের হারে এক বছর পর আপনার আমানতের মূল্য কত হবে? উত্তর হল $10.70 (10 + 10*0.07 =চক্রবৃদ্ধি সুদের সূত্রটি নিম্নরূপ:

=FV(0.08/12, 5*12, ,-2000)

যদি আপনার প্যারামিটারের কিছু ব্যাখ্যা প্রয়োজন, তাহলে আপনি এখানে যান:

• হার 0.008/12 যেহেতু আপনার আছে 8% বার্ষিক সুদের হার মাসিক চক্রবৃদ্ধি৷
• nper হল 5*12, অর্থাৎ 5 বছর * 12 মাস
• pmt ফাঁকা রাখা হয়েছে কারণ আমাদের কাছে কোনও অতিরিক্ত অর্থপ্রদান নেই৷
• pv হল -2000 যেহেতু এটি একটি আউটফ্লো এবং একটি নেতিবাচক সংখ্যা দ্বারা প্রতিনিধিত্ব করা উচিত৷

একটি খালি ঘরে উপরের সূত্রটি প্রবেশ করান, এবং এটি ফলাফল হিসাবে $2,979.69 আউটপুট করবে (যা পুরোপুরি ইনলাইন মাসিক চক্রবৃদ্ধি সুদের উদাহরণে সম্পাদিত গণিত গণনার ফলাফল।

স্বাভাবিকভাবে, সেল রেফারেন্সের সাথে মানগুলি প্রতিস্থাপন করতে আপনাকে কিছুই বাধা দেয় না:

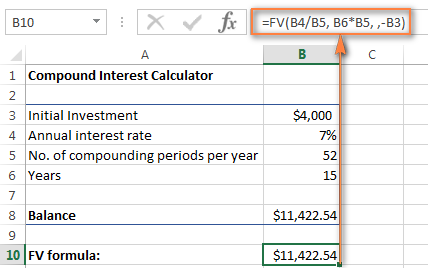
=FV(B4/B5, B6*B5, , -B3)

নীচের স্ক্রিনশটটি দেখায় 7% চক্রবৃদ্ধি সাপ্তাহিক হারে 15 বছর পর $4,000 বিনিয়োগের ভবিষ্যত মূল্য:

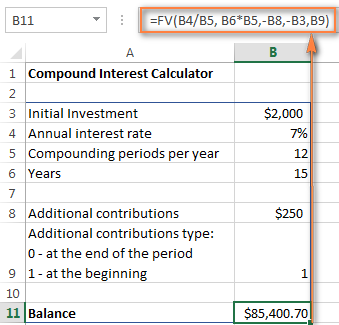
আপনার এক্সেল চক্রবৃদ্ধি সুদের ক্যালকুলেটরকে আরও শক্তিশালী করতে, আপনি এটি প্রসারিত করতে পারেন অতিরিক্ত অবদান বিকল্পের সাথে n (অতিরিক্ত অর্থপ্রদান) এবং সেই অনুযায়ী চক্রবৃদ্ধি সুদের সূত্র পরিবর্তন করুন।

=FV(B4/B5, B6*B5, -B8, -B3, B9)

কোথায়:

• B3 - মূল বিনিয়োগ
• B4 - বার্ষিক সুদের হার
• B5 - প্রতি বছর চক্রবৃদ্ধি সময়ের সংখ্যা
• B6 - সংরক্ষণ করার জন্য বছরের সংখ্যা
• B8 - অতিরিক্ত অবদান (ঐচ্ছিক)
• B9 - অতিরিক্ত অবদানের ধরন। মনে রাখবেন যে আপনি একটি জমা দিলে আপনি 1 লিখবেনচক্রবৃদ্ধি সময়ের শুরুতে অতিরিক্ত পরিমাণ, 0 বা বাদ দেওয়া হয় যদি মেয়াদ শেষে অতিরিক্ত অর্থ প্রদান করা হয়।

আপনি যদি এটি চেষ্টা করতে আগ্রহী হন এক্সেলের জন্য উন্নত যৌগিক সুদের ক্যালকুলেটর আপনার সঞ্চয় গণনা করার জন্য, আপনি এই পোস্টের শেষে এটি ডাউনলোড করতে পারেন।

টিপ। চক্রবৃদ্ধি সুদ গণনা করার আরেকটি দ্রুত উপায় হল এক্সেল ডেটা টেবিলের সাহায্যে কী-ইফ বিশ্লেষণ করা।

চৌগিক সুদের ক্যালকুলেটর অনলাইনে

আপনি যদি সময় না করে অর্থ বিনিয়োগ করতে পছন্দ করেন তবে কীভাবে তা খুঁজে বের করতে চান এক্সেলে চক্রবৃদ্ধি সুদ গণনা করতে, অনলাইন চক্রবৃদ্ধি সুদের ক্যালকুলেটর কাজে আসতে পারে। আপনি আপনার পছন্দের সার্চ ইঞ্জিনে "কম্পাউন্ড ইন্টারেস্ট ক্যালকুলেটর" এর মতো কিছু প্রবেশ করে তাদের প্রচুর খুঁজে পেতে পারেন। এর মধ্যে, আমাকে দ্রুত আমার প্রিয় কয়েকটি উপস্থাপন করতে দিন।

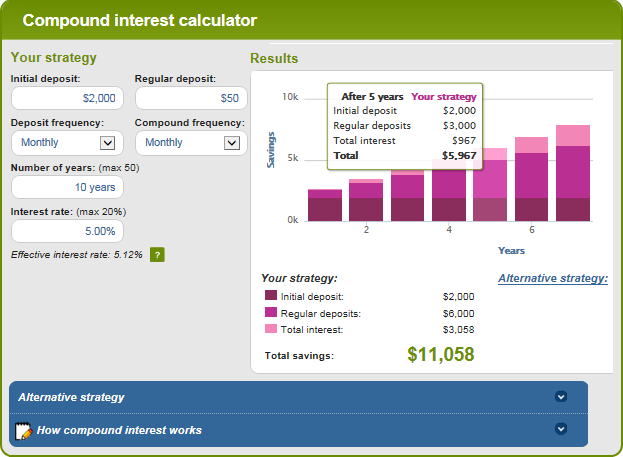
ব্যাঙ্করেটের চক্রবৃদ্ধি সুদের ক্যালকুলেটর

ব্যাঙ্করেট চক্রবৃদ্ধি সুদের ক্যালকুলেটরের মূল সুবিধা হল ব্যবহার-অবশ্য এবং ভিজ্যুয়াল উপস্থাপনা ফলাফলগুলো. এই ক্যালকুলেটরটি আপনাকে বাক্সে বা স্লাইডার সরানোর মাধ্যমে ম্যানুয়ালি সেভিংস ইনপুট প্রবেশ করতে দেয়। আপনি এটি করার সাথে সাথে, আনুমানিক মোট উপরে প্রদর্শিত হবে এবং নীচের গ্রাফে অবিলম্বে প্রতিফলিত হবে:

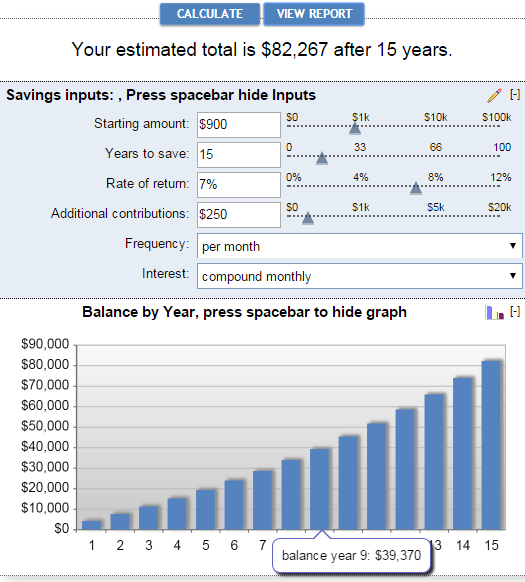
প্রতিবেদন দেখুন বোতামে ক্লিক করলে একটি "সারাংশ তৈরি হয় প্রতিবেদন" এর পাশাপাশি "সঞ্চয় ব্যালেন্স" যা অতিরিক্ত অবদানের পরিমাণ, অর্জিত সুদ এবং ব্যালেন্সের বিস্তারিত তথ্য প্রদান করেপ্রতি বছরের জন্য।

মানি-জাইন দ্বারা চক্রবৃদ্ধি সুদের ক্যালকুলেটর

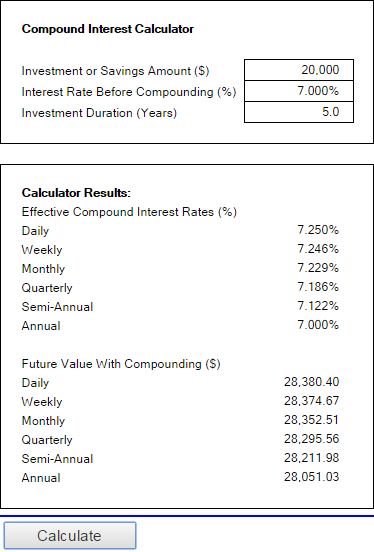
মানি-জাইন থেকে অনলাইন ক্যালকুলেটরটি ব্যাঙ্করেটের তুলনায় অনেক সহজ। এটি আপনাকে শুধুমাত্র 3টি মান নির্দিষ্ট করতে বলে: মূল বিনিয়োগ, সুদের হার এবং সময়কাল। যত তাড়াতাড়ি আপনি এই সংখ্যাগুলি সরবরাহ করবেন এবং গণনা করুন বোতামে ক্লিক করুন, এটি আপনাকে সমস্ত ধরণের চক্রবৃদ্ধি সুদের হার (দৈনিক, সাপ্তাহিক, মাসিক, বার্ষিক, ইত্যাদি) এবং সেইসাথে ভবিষ্যতের মানগুলি দেখাবে। চক্রবৃদ্ধি।

মনিস্মার্টের চক্রবৃদ্ধি সুদের ক্যালকুলেটর

এটি অস্ট্রেলিয়ান সিকিউরিটিজ অ্যান্ড ইনভেস্টমেন্ট কমিশন দ্বারা পরিচালিত একটি সত্যিই চমৎকার অনলাইন চক্রবৃদ্ধি সুদের ক্যালকুলেটর। এটি আপনাকে সমস্ত প্রাসঙ্গিক কারণগুলি ইনপুট করতে দেয় যা আপনার বিনিয়োগের ভবিষ্যত মূল্য নির্ধারণ করে এবং ফলাফলটিকে একটি গ্রাফ হিসাবে আউটপুট করে। গ্রাফে একটি নির্দিষ্ট বারের উপরে হোভার করে, আপনি সেই নির্দিষ্ট বছরের জন্য সারসংক্ষেপ তথ্য দেখতে পারেন।

এভাবে আপনি এক্সেল এবং এর বাইরে চক্রবৃদ্ধি সুদের হিসাব করবেন :) আমি আশা করি এই নিবন্ধে আলোচিত অন্তত একটি চক্রবৃদ্ধি সুদের সূত্র আপনার জন্য সহায়ক প্রমাণিত হয়েছে। যাইহোক, আমি পড়ার জন্য আপনাকে ধন্যবাদ এবং আশা করি আগামী সপ্তাহে আমাদের ব্লগে আপনাকে দেখতে পাব!

ডাউনলোডের জন্য ওয়ার্কবুক অনুশীলন করুন

এক্সেলের জন্য যৌগিক সুদ ক্যালকুলেটর (.xlsx ফাইল)

চৌগিক সুদের ক্ষেত্রে , প্রতিটি সময়ের মধ্যে মূল আলাদা। ব্যাঙ্ক আপনাকে অর্জিত সুদ ফেরত দেবে না, পরিবর্তে তারা এটি আপনার মূল বিনিয়োগে যোগ করে। এই বর্ধিত পরিমাণ পরবর্তী সময়কালের জন্য মূল হয়ে ওঠে (চক্রীকরণ সময়কাল) এবং সুদও অর্জন করে। অন্য কথায়, আপনি শুধুমাত্র মূল পরিমাণের উপর নয়, প্রতিটি চক্রবৃদ্ধি সময়ের মধ্যে অর্জিত সুদের উপরও সুদ অর্জন করেন।

আমাদের উদাহরণে, $10 এর মূল পরিমাণ ছাড়াও, $0.70 এর অর্জিত সুদ হবে পরের বছর সুদও পান। তাহলে, বার্ষিক 7% চক্রবৃদ্ধি হারে 2 বছর পর আপনার $10 আমানতের মূল্য কত হবে? উত্তর হল $11.45 (10.7 + 10.7*0.07 = 11.45) এবং আপনার অর্জিত সুদ হল $1.45। যেমন আপনি দেখতে পাচ্ছেন, দ্বিতীয় বছরের শেষে, আপনি প্রাথমিক $10 ডিপোজিটের উপর শুধুমাত্র $0.70 উপার্জন করেননি, আপনি প্রথম বছরে জমা হওয়া $0.70 সুদের উপর $0.05 উপার্জন করেছেন।

এক্সেলে চক্রবৃদ্ধি সুদ গণনা করার বিভিন্ন উপায় রয়েছে, এবং আমরা প্রতিটির বিস্তারিত আলোচনা করতে যাচ্ছি।

এক্সেলে চক্রবৃদ্ধি সুদের হিসাব কীভাবে করা যায়

দীর্ঘ সময়ের বিনিয়োগ আপনার সম্পদ বাড়ানোর জন্য একটি কার্যকর কৌশল হতে পারে, এবং এমনকি ছোট আমানত সময়ের সাথে সাথে একটি বড় পার্থক্য করতে পারে। এক্সেল যৌগিক সুদের সূত্রগুলি আরও ব্যাখ্যা করা আপনাকে সঞ্চয় কৌশল পেতে সাহায্য করবেকাজ অবশেষে, আমরা একটি সার্বজনীন সূত্র তৈরি করতে যাচ্ছি যা বিভিন্ন চক্রবৃদ্ধি সময়কালের সাথে ভবিষ্যত মান গণনা করে - দৈনিক, সাপ্তাহিক, মাসিক, ত্রৈমাসিক বা বার্ষিক।

এক্সেলে বার্ষিক চক্রবৃদ্ধি সুদের হিসাব করা

প্রতি চক্রবৃদ্ধি সুদের ধারণাটি আরও ভালভাবে বুঝতে, আসুন এই টিউটোরিয়ালের শুরুতে আলোচিত একটি খুব সাধারণ উদাহরণ দিয়ে শুরু করি এবং এক্সেলে বার্ষিক চক্রবৃদ্ধি সুদের গণনা করার জন্য একটি সূত্র লিখি। আপনার মনে আছে, আপনি বার্ষিক 7% সুদের হারে $10 বিনিয়োগ করছেন এবং বার্ষিক চক্রবৃদ্ধি কীভাবে আপনার সঞ্চয় বাড়ায় তা জানতে চান।

বার্ষিক চক্রবৃদ্ধি সুদ - সূত্র 1

একটি সহজ এবং সরল উপায় বার্ষিক চক্রবৃদ্ধি সুদের সাথে অর্জিত পরিমাণ গণনা করার জন্য একটি সংখ্যাকে শতাংশ দ্বারা বৃদ্ধি করার জন্য সূত্র ব্যবহার করা হয়:

=Amount * (1 + %) ।

আমাদের উদাহরণে, সূত্রটি হল:

=A2*(1+$B2)

যেখানে A2 হল আপনার প্রাথমিক আমানত এবং B2 হল বার্ষিক সুদের হার৷ অনুগ্রহ করে মনোযোগ দিন যে আমরা $ চিহ্ন ব্যবহার করে কলাম B এর রেফারেন্স ঠিক করি।

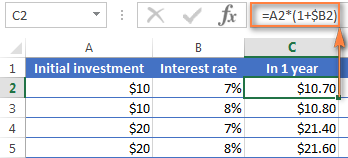
আপনার মনে আছে, 1% হল একশোর একটি অংশ, অর্থাৎ 0.01, তাই 7 % হল 0.07, এবং এইভাবে শতাংশ আসলে Excel এ সংরক্ষণ করা হয়। এটি মাথায় রেখে, আপনি 10*(1+0.07) বা 10*1.07 এর একটি সাধারণ গণনা সম্পাদন করে সূত্র দ্বারা প্রত্যাবর্তিত ফলাফল যাচাই করতে পারেন এবং নিশ্চিত করুন যে 1 বছর পরে আপনার ব্যালেন্স প্রকৃতপক্ষে $10.70 হবে।

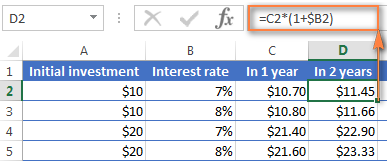
এবং এখন, 2 বছর পর ব্যালেন্স হিসাব করা যাক। তা কিভাবেআপনার $10 ডিপোজিটের মূল্য কি দুই বছরের মধ্যে 7% বার্ষিক সুদের হারে হবে? উত্তরটি হল $11.45 এবং আপনি ডি কলামে একই সূত্র অনুলিপি করে এটি পেতে পারেন।

3 এর শেষে আপনি আপনার ব্যাঙ্ক অ্যাকাউন্টে কত টাকা পাবেন তা গণনা করতে বছর, শুধু কলাম E এ একই সূত্র অনুলিপি করুন এবং আপনি $12.25 পাবেন।

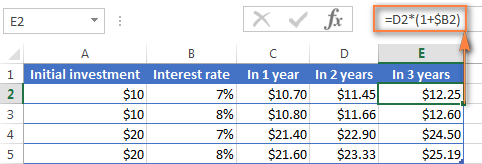
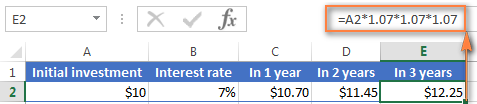
আপনার মধ্যে যাদের এক্সেল সূত্র সম্পর্কে কিছু অভিজ্ঞতা আছে তারা সম্ভবত বুঝতে পেরেছেন যে উপরের সূত্রটি কী প্রকৃতপক্ষে $10 এর প্রাথমিক জমাকে 1.07 দ্বারা তিনবার গুণ করা হচ্ছে:

=10*1.07*1.07*1.07=12.25043

এটিকে দুই দশমিক স্থানে রাউন্ড করুন এবং আপনি উপরের স্ক্রিনশটে E2 সেলের মতো একই নম্বর পাবেন - $12.25। স্বাভাবিকভাবেই, আপনি এই সূত্রটি ব্যবহার করে 3 বছর পর সরাসরি ব্যালেন্স গণনা করতে পারেন:

=A2*1.07*1.07*1.07

বার্ষিক চক্রবৃদ্ধি সুদ - সূত্র 2

আরেকটি একটি বার্ষিক চক্রবৃদ্ধি সুদের সূত্র তৈরি করার উপায় হল প্রতি বছরের জন্য অর্জিত সুদ গণনা করা এবং তারপরে এটি প্রাথমিক জমাতে যোগ করা।

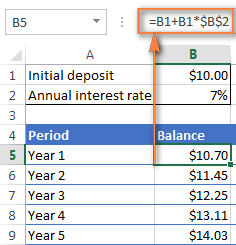
ধরে নেওয়া হচ্ছে যে আপনার প্রাথমিক আমানত সেল B1 এবং <1 এ রয়েছে>বার্ষিক সুদের হার সেল B2-এ, নিম্নলিখিত সূত্রটি একটি ট্রিট কাজ করে:

=B1 + B1 * $B$2

সূত্রটি সঠিকভাবে কাজ করার জন্য, অনুগ্রহ করে মনে রাখবেন নিম্নলিখিত বিবরণ:

• $ চিহ্ন যোগ করে বার্ষিক সুদের হার সেলের রেফারেন্স ঠিক করুন (আমাদের ক্ষেত্রে B2) এটি একটি পরম কলাম এবং পরম সারি হওয়া উচিত, যেমন $B$2।
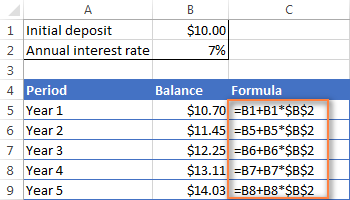
• বছর 2 (B6) এর জন্যএবং পরবর্তী সমস্ত বছর, সূত্রটি এতে পরিবর্তন করুন:

  বছর 1 ব্যালেন্স + বছর 1 ব্যালেন্স * সুদের হার

এই উদাহরণে, আপনি সেল B6-এ নিম্নলিখিত সূত্রটি লিখবেন এবং তারপর অন্য সারিগুলিতে অনুলিপি করুন, যেমন নীচের স্ক্রিনশটে দেখানো হয়েছে:

=B5 + B5 * $B$2

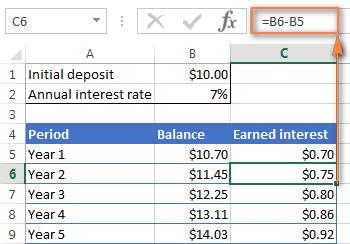
বার্ষিক চক্রবৃদ্ধি দিয়ে আপনি আসলে কতটা সুদ অর্জন করেছেন তা খুঁজে বের করতে, প্রাথমিক জমা (B1) 1 বছর পরে ব্যালেন্স থেকে (B5) বিয়োগ করুন। এই সূত্রটি C5-এ যায়:

=B5-B1

C6-এ, 2 বছর পরের ব্যালেন্স থেকে 1 বছর পরে ব্যালেন্স বিয়োগ করুন এবং সূত্রটি নীচে টেনে আনুন অন্যান্য কক্ষে:

=B6-B5

আপনি নীচের স্ক্রিনশটের মত অর্জিত আগ্রহ বৃদ্ধি দেখতে পাবেন।

উপরের উদাহরণগুলি চক্রবৃদ্ধি সুদের ধারণাকে ব্যাখ্যা করে একটি ভাল কাজ করে, তাই না? কিন্তু কোনো সূত্রই এক্সেলের জন্য সার্বজনীন যৌগিক সুদের সূত্র বলা যথেষ্ট ভালো নয়। প্রথমত, কারণ তারা আপনাকে একটি কম্পাউন্ডিং ফ্রিকোয়েন্সি নির্দিষ্ট করতে দেয় না, এবং দ্বিতীয়ত, কারণ আপনাকে কেবল একটি নির্দিষ্ট সময়কাল এবং সুদের হার প্রবেশ করার পরিবর্তে একটি সম্পূর্ণ টেবিল তৈরি করতে হবে৷

আচ্ছা, আসুন এক ধাপ এগিয়ে যাই এবং তৈরি করি এক্সেলের জন্য একটি সর্বজনীন চক্রবৃদ্ধি সুদের সূত্র যা হিসাব করতে পারে যে আপনি বার্ষিক, ত্রৈমাসিক, মাসিক, সাপ্তাহিক বা দৈনিক চক্রবৃদ্ধি দিয়ে কত টাকা উপার্জন করবেন।

সাধারণ চক্রবৃদ্ধি সুদের সূত্র

যখন আর্থিক উপদেষ্টারা প্রভাব বিশ্লেষণ করেন একটি চক্রবৃদ্ধি সুদেরবিনিয়োগ, তারা সাধারণত তিনটি বিষয় বিবেচনা করে যা বিনিয়োগের ভবিষ্যৎ মূল্য নির্ধারণ করে (FV):

• PV - বিনিয়োগের বর্তমান মূল্য
• i - প্রতিটি মেয়াদে অর্জিত সুদের হার
• n - সময়ের সংখ্যা

এই উপাদানগুলি জেনে, আপনি একটি নির্দিষ্ট চক্রবৃদ্ধি সুদের হার সহ বিনিয়োগের ভবিষ্যত মূল্য পেতে নিম্নলিখিত সূত্রটি ব্যবহার করতে পারেন :

বিন্দুটিকে আরও ভালভাবে বোঝাতে, এখানে কয়েকটি দ্রুত উদাহরণ দেওয়া হল।

উদাহরণ 1: মাসিক চক্রবৃদ্ধি সুদের সূত্র

ধরুন, আপনি মাসিক চক্রবৃদ্ধি হারে 8% সুদের হারে $2,000 বিনিয়োগ করেন এবং আপনি 5 বছর পরে আপনার বিনিয়োগের মূল্য জানতে চান।

প্রথমে, আসুন আপনার চক্রবৃদ্ধি সুদের সূত্রের জন্য উপাদানগুলির একটি তালিকা লিখুন:<3

• PV = $2,000
• i = 8% প্রতি বছর, চক্রবৃদ্ধি মাসিক (0.08/12= 006666667)
• n = 5 বছর x 12 মাস (5*12= 60)

উপরের নম্বরগুলি সূত্রে ইনপুট করুন, এবং আপনি পাবেন:

= $2,000 * (1 + 0.8/12)5x12

বা

= $2,000 * 1.00666666760

অথবা

= $2,000 * 1.489845708 = $2,979.69 <3

উদাহরণ 2: দৈনিক চক্রবৃদ্ধি সুদের সূত্র

আমি আশা করি মাসিক চক্রবৃদ্ধি সুদের উদাহরণটি ভালভাবে বোঝা গেছে, এবং এখন আপনি দৈনিক চক্রবৃদ্ধির জন্য একই পদ্ধতি ব্যবহার করতে পারেন। প্রাথমিক বিনিয়োগ, সুদের হার, সময়কাল এবং সূত্র ঠিক উপরের উদাহরণের মতোই, শুধুমাত্র চক্রবৃদ্ধি সময়কাল ভিন্ন:

• PV = $2,000
• i = 8% প্রতি বছর, দৈনিক চক্রবৃদ্ধি(0.08/365 = 0.000219178)
• n = 5 বছর x 365 দিন (5*365 = 1825)

উপরের সংখ্যাগুলি চক্রবৃদ্ধি সুদের সূত্রে সরবরাহ করুন এবং আপনি পাবেন নিম্নলিখিত ফলাফল:

=$2,000 * (1 + 0.000219178)1825 = $2,983.52

যেমন আপনি দেখতে পাচ্ছেন, দৈনিক চক্রবৃদ্ধি সুদের সাথে, একই বিনিয়োগের ভবিষ্যৎ মূল্য মাসিক চক্রবৃদ্ধির তুলনায় একটু বেশি। এর কারণ হল 8% সুদের হার প্রতিটি মাসের চেয়ে প্রতিদিন মূল পরিমাণে সুদ যোগ করে। আপনি যেমন অনুমান করতে পারেন, মাসিক চক্রবৃদ্ধি ফলাফল বার্ষিক চক্রবৃদ্ধি থেকে বেশি হবে৷

এগুলি সবই ভাল, কিন্তু আপনি যা চান তা হল চক্রবৃদ্ধি সুদের জন্য একটি এক্সেল সূত্র, তাই না? একটু বেশি সময় সহ্য করুন, অনুগ্রহ করে। এখন আমরা সবচেয়ে আকর্ষণীয় অংশে যাচ্ছি - এক্সেলে আপনার নিজস্ব শক্তিশালী এবং বহুমুখী যৌগিক সুদের ক্যালকুলেটর তৈরি করা।

এক্সেলে চক্রবৃদ্ধি সুদের সূত্র (দৈনিক, সাপ্তাহিক, মাসিক, বার্ষিক চক্রবৃদ্ধি)

সাধারণত , এক্সেলে কিছু করার একাধিক উপায় রয়েছে এবং একটি চক্রবৃদ্ধি সুদের সূত্র একটি ব্যতিক্রম নয় :) যদিও মাইক্রোসফ্ট এক্সেল চক্রবৃদ্ধি সুদ গণনা করার জন্য কোন বিশেষ ফাংশন প্রদান করে না, আপনি আপনার নিজস্ব যৌগিক সুদের ক্যালকুলেটর তৈরি করতে অন্যান্য ফাংশন ব্যবহার করতে পারেন৷

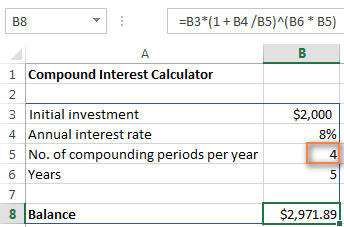
আসুন এক্সেল ওয়ার্কশীটে বিনিয়োগের ভবিষ্যৎ মূল্য নির্ধারণ করে এমন মৌলিক বিষয়গুলি প্রবেশ করে আমাদের এক্সেল যৌগিক সুদের ক্যালকুলেটর তৈরি করা শুরু করি:

• প্রাথমিক বিনিয়োগ (B3)
• বার্ষিক সুদের হার(B4)
• প্রতি বছর কম্পাউন্ডিং পিরিয়ডের সংখ্যা (B5)
• বছরের সংখ্যা (B6)

সম্পন্ন হলে, আপনার এক্সেল শীট এর মতো দেখতে হতে পারে :

ইনপুট মানের উপর ভিত্তি করে অর্জিত পরিমাণ (ব্যালেন্স) গণনা করার জন্য এখন আপনার যা দরকার তা হল চক্রবৃদ্ধি সুদের সূত্র। সেরা খবর হল যে আপনাকে চাকাটি পুনরায় উদ্ভাবন করতে হবে না। আমরা কেবল ব্যাঙ্কিং এবং অন্যান্য আর্থিক প্রতিষ্ঠানগুলির দ্বারা ব্যবহৃত সময়-পরীক্ষিত চক্রবৃদ্ধি সুদের সূত্রটি নেব এবং এটিকে এক্সেলের ভাষায় অনুবাদ করব৷

এক্সেলের জন্য চক্রবৃদ্ধি সুদের সূত্র:

উপরের উত্স ডেটার জন্য, সূত্রটি এই আকার নেয়:

=B3 * (1 + B4 /B5) ^ (B6 * B5)

25>

সংখ্যাগুলি বরং পরিচিত দেখাচ্ছে? হ্যাঁ, এই একই মান এবং গণনা যা আমরা একটি মাসিক চক্রবৃদ্ধি সুদের সূত্র দিয়ে করেছি, এবং ফলাফল প্রমাণ করে যে আমরা সবকিছু ঠিকঠাক করেছি!

আপনি যদি জানতে চান আপনার বিনিয়োগের মূল্য কত হবে একটি 8% বার্ষিক সুদের হার চক্রবৃদ্ধি ত্রৈমাসিক , কেবল সেল B5-এ 4 লিখুন:

আপনার বিনিয়োগের ভবিষ্যত মূল্য গণনা করতে সেমি -বার্ষিক চক্রবৃদ্ধি, প্রতি বছর যৌগিক সময়কাল মান হিসাবে 2 লিখুন। সাপ্তাহিক সুদের হারের জন্য, 52 লিখুন, প্রতি বছর কত সপ্তাহ থাকে। আপনি আগ্রহী হলে দৈনিক চক্রবৃদ্ধি, 365 লিখুন, ইত্যাদি।

অর্জিত সুদের পরিমাণ খুঁজে পেতে, কেবল ভবিষ্যতের মান (ব্যালেন্স) এবং বর্তমানের মধ্যে পার্থক্য গণনা করুন মূল্য (প্রাথমিক বিনিয়োগ)। আমাদের ক্ষেত্রে, B9-এর সূত্রটি যতটা সহজ:

=B8-B3

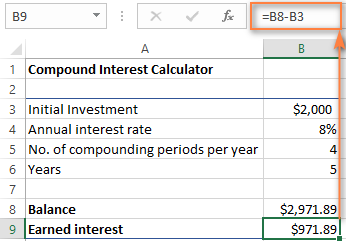
যেমন আপনি দেখতে পাচ্ছেন, আমরা এর জন্য একটি সত্যই সর্বজনীন যৌগিক সুদের ক্যালকুলেটর তৈরি করেছি এক্সেল আশা করি, এখন আপনার কোনো অনুশোচনা নেই যে আপনি আর্থিক পরিকল্পনাবিদদের দ্বারা ব্যবহৃত জটিল চক্রবৃদ্ধি সুদের সূত্রটি বের করার জন্য কয়েক মূল্যবান মিনিট বিনিয়োগ করেছেন : )

Excel এর জন্য উন্নত চক্রবৃদ্ধি সুদের ক্যালকুলেটর

যদি কোনো কারণে আপনি উপরের পদ্ধতির সাথে পুরোপুরি সন্তুষ্ট নন, আপনি এফভি ফাংশন ব্যবহার করে আপনার এক্সেল কম্পাউন্ড ইন্টারেস্ট ক্যালকুলেটর তৈরি করতে পারেন যা Excel 2000 থেকে 2019 এর সমস্ত সংস্করণে পাওয়া যায়।

FV ফাংশন একটি বিনিয়োগের ভবিষ্যত মূল্য গণনা করে আমাদের আলোচনার মত ইনপুট ডেটার উপর ভিত্তি করে, যদিও এর সিনট্যাক্স একটু ভিন্ন:

আর্গুমেন্টের বিস্তারিত ব্যাখ্যা এক্সেল এফভি ফাংশন টিউটোরিয়ালে পাওয়া যাবে।

এর মধ্যে, আসুন মাসিক চক্রবৃদ্ধি সুদের উদাহরণের মতো একই উৎস ডেটা ব্যবহার করে একটি এফভি সূত্র তৈরি করি এবং দেখুন আমরা একই ফলাফল পাচ্ছি কিনা।

আপনার মনে থাকতে পারে, আমরা 5 বছরের জন্য $2,000 জমা দিয়েছিলাম একটি সঞ্চয় অ্যাকাউন্টে 8% বার্ষিক চক্রবৃদ্ধি হারে মাসিক, কোন অতিরিক্ত পেমেন্ট ছাড়া. সুতরাং, আমাদের