Spis treści
W tym tutorialu przyjrzymy się, jak zrobić analizę wariancji Excel i jakie formuły zastosować, aby znaleźć wariancję próbki i populacji.
Wariancja jest jednym z najbardziej przydatnych narzędzi w teorii prawdopodobieństwa i statystyce. W nauce opisuje, jak daleko każda liczba w zbiorze danych jest od średniej. W praktyce często pokazuje, jak bardzo coś się zmienia. Na przykład temperatura w pobliżu równika ma mniejszą wariancję niż w innych strefach klimatycznych. W tym artykule przeanalizujemy różne metody obliczania wariancji w Excelu.
Co to jest wariancja?
Wariancja Jest to miara zmienności zbioru danych, która wskazuje, jak bardzo różne wartości są rozłożone. Matematycznie definiuje się ją jako średnią kwadratową różnic od średniej.
Aby lepiej zrozumieć, co właściwie obliczasz z wariancją, rozważ ten prosty przykład.
Załóżmy, że w twoim lokalnym zoo jest 5 tygrysów, które mają 14, 10, 8, 6 i 2 lata.
Aby znaleźć wariancję, wykonaj te proste kroki:
- Oblicz średnią (średnią prostą) z pięciu liczb:
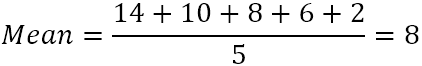
- Od każdej liczby odejmij średnią, aby znaleźć różnice. Aby to zwizualizować, wykreślmy różnice na wykresie:
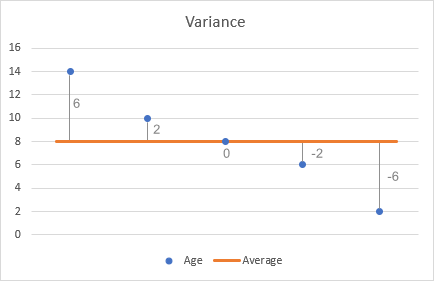
- Skwituj każdą różnicę.
- Opracuj średnią z różnic kwadratowych.
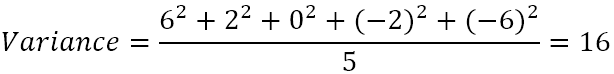
Wariancja wynosi więc 16. Ale co właściwie oznacza ta liczba?
W rzeczywistości wariancja daje tylko bardzo ogólne pojęcie o rozproszeniu zbioru danych. Wartość 0 oznacza brak zmienności, tzn. wszystkie liczby w zbiorze danych są takie same. Im większa liczba, tym bardziej rozproszone są dane.
Ten przykład dotyczy wariancji populacyjnej (tzn. 5 tygrysów to cała interesująca Cię grupa). Jeśli Twoje dane są wyborem z większej populacji, to musisz obliczyć wariancję z próby, stosując nieco inny wzór.
Jak obliczyć wariancję w programie Excel
W Excelu istnieje 6 wbudowanych funkcji do wykonywania wariancji: VAR, VAR.S, VARP, VAR.P, VARA i VARPA.
Twój wybór formuły wariancji zależy od następujących czynników:
- Wersja programu Excel, której używasz.
- Czy oblicza się wariancję próby czy populacji.
- Czy chcesz oceniać lub ignorować wartości tekstowe i logiczne.
Funkcje wariancji w programie Excel
Poniższa tabela zawiera przegląd funkcji wariacyjnych dostępnych w programie Excel, co pomoże Ci wybrać formułę najlepiej odpowiadającą Twoim potrzebom.
| Nazwa | Wersja dla programu Excel | Typ danych | Tekst i logika |
| VAR | 2000 - 2019 | Przykładowa strona | Zignorowano |
| VAR.S | 2010 - 2019 | Przykładowa strona | Zignorowano |
| VARA | 2000 - 2019 | Przykładowa strona | Oceniona |
| VARP | 2000 - 2019 | Ludność | Zignorowano |
| VAR.P | 2010 - 2019 | Ludność | Zignorowano |
| VARPA | 2000 - 2019 | Ludność | Oceniona |
VAR.S vs. VARA i VAR.P vs. VARPA
VARA i VARPA różnią się od innych funkcji wariancji jedynie sposobem, w jaki obsługują wartości logiczne i tekstowe w referencjach. Poniższa tabela zawiera podsumowanie sposobu, w jaki oceniane są tekstowe reprezentacje liczb i wartości logicznych.
| Typ argumentu | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Wartości logiczne w tablicach i odwołaniach | Zignorowano | Oceniona (TRUE=1, FALSE=0) |
| Tekstowe reprezentacje liczb w tablicach i odwołaniach | Zignorowano | Oceniane jako zero |
| Wartości logiczne i tekstowe reprezentacje liczb wpisywane bezpośrednio do argumentów | Oceniona (TRUE=1, FALSE=0) | |
| Puste komórki | Zignorowano | |
Jak obliczyć wariancję próby w Excelu
A przykład to zbiór danych wyodrębnionych z całej populacji. A wariancję obliczoną z próby nazywamy wariancja próby .
Na przykład, jeśli chcesz wiedzieć, jak zmieniają się wysokości ludzi, zmierzenie każdej osoby na ziemi byłoby technicznie niewykonalne. Rozwiązaniem jest pobranie próbki populacji, powiedzmy 1000 osób, i oszacowanie wysokości całej populacji na podstawie tej próbki.
Wariancję próby oblicza się za pomocą tego wzoru:
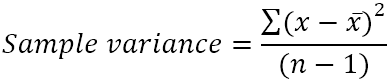
Gdzie:
- x̄ to średnia (średnia prosta) wartości z próby.
- n to wielkość próby, czyli liczba wartości w próbie.
W Excelu istnieją 3 funkcje pozwalające znaleźć wariancję z próby: VAR, VAR.S i VARA.
Funkcja VAR w programie Excel
Jest to najstarsza funkcja Excela służąca do szacowania wariancji na podstawie próbki. Funkcja VAR jest dostępna we wszystkich wersjach Excela od 2000 do 2019 roku.
VAR(liczba1, [liczba2], ...)Uwaga. W programie Excel 2010 funkcja VAR została zastąpiona funkcją VAR.S, która zapewnia lepszą dokładność. Chociaż funkcja VAR jest nadal dostępna w celu zapewnienia kompatybilności wstecznej, zaleca się korzystanie z funkcji VAR.S w bieżących wersjach programu Excel.
Funkcja VAR.S w programie Excel
Jest to nowoczesny odpowiednik funkcji VAR programu Excel. Użyj funkcji VAR.S, aby znaleźć wariancję próbki w programie Excel 2010 i nowszych.
VAR.S(liczba1, [liczba2], ...)Funkcja VARA w programie Excel
Funkcja VARA programu Excel zwraca przykładową wariancję na podstawie zestawu liczb, tekstu i wartości logicznych, jak pokazano w tej tabeli.
VARA(wartość1, [wartość2], ...)Przykładowa formuła wariancji w Excelu
Podczas pracy z numerycznym zestawem danych możesz użyć dowolnej z powyższych funkcji, aby obliczyć wariancję próbki w programie Excel.
Jako przykład znajdźmy wariancję próby składającej się z 6 elementów (B2:B7). W tym celu można skorzystać z jednego z poniższych wzorów:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Jak widać na zrzucie ekranu, wszystkie formuły zwracają ten sam wynik (zaokrąglony do 2 miejsc po przecinku):
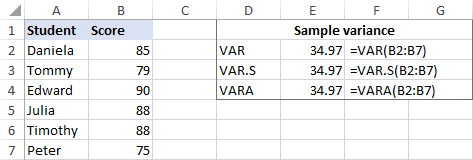
Aby sprawdzić wynik, wykonajmy ręcznie obliczenia var:
- Znajdź średnią za pomocą funkcji AVERAGE:
= ŚREDNIA(B2:B7)Średnia trafia do dowolnej pustej komórki, powiedzmy B8.
- Odejmij średnią od każdej liczby w próbie:
=B2-$B$8Różnice przechodzą do kolumny C, zaczynając od C2.
- Każdą różnicę podnieść do kwadratu, a wyniki umieścić w kolumnie D, zaczynając od D2:
=C2^2 - Zsumuj różnice kwadratowe i podziel wynik przez liczbę przedmiotów w próbie minus 1:
=SUMA(D2:D7)/(6-1)
Jak widać, wynik naszego ręcznego obliczenia var jest dokładnie taki sam jak liczba zwracana przez wbudowane funkcje Excela:
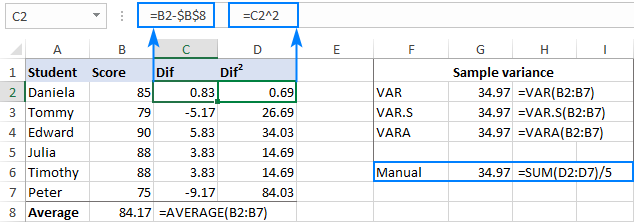
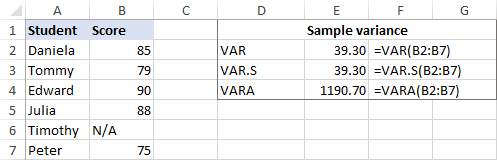
Jeśli twój zestaw danych zawiera Boolean i/lub tekst funkcja VARA zwróci inny wynik. Powodem jest to, że VAR i VAR.S ignorują wszelkie wartości inne niż liczby w referencjach, podczas gdy VARA ocenia wartości tekstowe jako zera, TRUE jako 1, a FALSE jako 0. Tak więc, proszę starannie wybrać funkcję wariancji dla swoich obliczeń w zależności od tego, czy chcesz przetwarzać lub ignorować tekst i logiki.
Jak obliczyć wariancję populacji w Excelu
Ludność to wszyscy członkowie danej grupy, czyli wszystkie obserwacje w badanej dziedzinie. Wariancja populacji opisuje, jak rozłożone są punkty danych w całej populacji.
Wariancję populacji można znaleźć za pomocą tego wzoru:
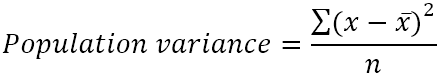
Gdzie:
- x̄ to średnia z populacji.
- n to wielkość populacji, czyli całkowita liczba wartości w populacji.
W Excelu istnieją 3 funkcje do obliczania wariancji populacji: VARP, VAR.P i VARPA.
Funkcja VARP w programie Excel
Funkcja Excel VARP zwraca wariancję populacji na podstawie całego zbioru liczb. Jest ona dostępna we wszystkich wersjach Excela od 2000 do 2019.
VARP(liczba1, [liczba2], ...)Uwaga. W programie Excel 2010 funkcja VARP została zastąpiona funkcją VAR.P, ale nadal jest zachowana w celu zapewnienia kompatybilności wstecznej. Zaleca się stosowanie funkcji VAR.P w obecnych wersjach programu Excel, ponieważ nie ma gwarancji, że funkcja VARP będzie dostępna w przyszłych wersjach programu Excel.
Funkcja VAR.P w programie Excel
Jest to ulepszona wersja funkcji VARP dostępnej w programie Excel 2010 i nowszych.
VAR.P(liczba1, [liczba2], ...)Funkcja VARPA w programie Excel
Funkcja VARPA oblicza wariancję populacji na podstawie całego zestawu liczb, tekstu i wartości logicznych. Jest dostępna we wszystkich wersjach Excela od 2000 do 2019.
VARA(wartość1, [wartość2], ...)Formuła wariancji populacji w Excelu
W przykładowym przykładzie obliczania wariancji znaleźliśmy wariancję wyników 5 egzaminów przy założeniu, że wyniki te były wyborem z większej grupy studentów. Jeśli zbierzesz dane o wszystkich studentach w grupie, dane te będą reprezentować całą populację i obliczysz wariancję populacji, korzystając z powyższych funkcji.
Załóżmy, że mamy wyniki egzaminów grupy 10 studentów (B2:B11). Wyniki te stanowią całą populację, więc będziemy robić wariancję za pomocą tych wzorów:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
I wszystkie formuły zwrócą identyczny wynik:
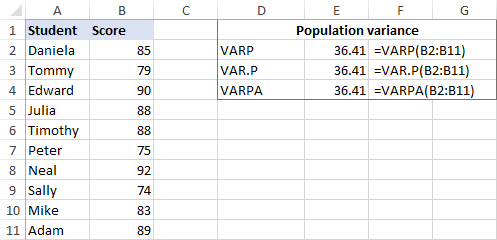
Aby upewnić się, że Excel wykonał wariancję poprawnie, możesz sprawdzić ją za pomocą ręcznej formuły obliczania var pokazanej na zrzucie ekranu poniżej:

Jeśli niektórzy studenci nie przystąpili do egzaminu i zamiast numeru wyniku mają N/A, funkcja VARPA zwróci inny wynik. Powodem jest to, że VARPA ocenia wartości tekstowe jako zera, podczas gdy VARP i VAR.P ignorują wartości tekstowe i logiczne w referencjach. Proszę zobaczyć VAR.P vs. VARPA, aby uzyskać pełne szczegóły.

Formuła wariancji w Excelu - uwagi użytkowe
Aby poprawnie wykonać analizę wariancji w Excelu, należy przestrzegać tych prostych zasad:
- Podaj argumenty jako wartości, tablice lub odwołania do komórek.
- W Excelu 2007 i nowszych można podać do 255 argumentów odpowiadających próbce lub populacji; w Excelu 2003 i starszych - do 30 argumentów.
- Aby ocenić tylko numery w odwołaniach, ignorując puste komórki, tekst i wartości logiczne, użyj funkcji VAR lub VAR.S, aby obliczyć wariancję próbki i VARP lub VAR.P, aby znaleźć wariancję populacji.
- Ocenić logiczne oraz tekst wartości w referencjach, należy użyć funkcji VARA lub VARPA.
- Zapewnić co najmniej dwie wartości numeryczne do wzoru na wariancję próby i co najmniej jedna wartość liczbowa do formuły wariancji populacji w Excelu, w przeciwnym razie pojawi się błąd #DIV/0!
- Argumenty zawierające tekst, który nie może być interpretowany jako liczby, powodują błędy #VALUE!
Wariancja a odchylenie standardowe w Excelu
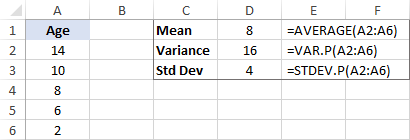
Wariancja jest niewątpliwie użytecznym pojęciem w nauce, ale daje bardzo mało praktycznych informacji. Na przykład, znaleźliśmy wiek populacji tygrysów w lokalnym zoo i obliczyliśmy wariancję, która jest równa 16. Pytanie brzmi - jak faktycznie możemy wykorzystać tę liczbę?
Możesz użyć wariancji do opracowania odchylenia standardowego, które jest znacznie lepszą miarą ilości zmienności w zestawie danych.
Odchylenie standardowe obliczamy jako pierwiastek kwadratowy z wariancji. Zatem bierzemy pierwiastek kwadratowy z 16 i otrzymujemy odchylenie standardowe równe 4.
W połączeniu ze średnią, odchylenie standardowe może powiedzieć, ile lat ma większość tygrysów. Na przykład, jeśli średnia wynosi 8, a odchylenie standardowe 4, większość tygrysów w zoo ma od 4 lat (8 - 4) do 12 lat (8 + 4).
Program Microsoft Excel posiada specjalne funkcje umożliwiające opracowanie odchylenia standardowego dla próbki i populacji. Szczegółowe wyjaśnienie wszystkich funkcji można znaleźć w tym poradniku: Jak obliczyć odchylenie standardowe w programie Excel.
Oto jak zrobić wariancję w Excelu. Aby przyjrzeć się bliżej formułom omawianym w tym tutorialu, zapraszamy do pobrania naszego przykładowego skoroszytu na końcu tego postu. Dziękuję za przeczytanie i mam nadzieję, że zobaczymy się na naszym blogu w przyszłym tygodniu!
Zeszyt ćwiczeń
Obliczanie wariancji w Excelu - przykłady (plik .xlsx)

