Innehållsförteckning
I den här handledningen kommer vi att titta på hur man gör variansanalyser i Excel och vilka formler man ska använda för att hitta variansen för ett urval och en population.
Varians är ett av de mest användbara verktygen inom sannolikhetsteori och statistik. Inom vetenskapen beskriver den hur långt varje tal i datamängden är från medelvärdet. I praktiken visar den ofta hur mycket något förändras. Exempelvis har temperaturen nära ekvatorn mindre varians än i andra klimatzoner. I den här artikeln kommer vi att analysera olika metoder för att beräkna varians i Excel.
Vad är varians?
Avvikelse är ett mått på variabiliteten i en datamängd som anger hur långt olika värden är spridda. Matematiskt definieras det som genomsnittet av de kvadrerade skillnaderna från medelvärdet.
För att bättre förstå vad du egentligen beräknar med variansen kan du ta detta enkla exempel.
Antag att det finns fem tigrar i din lokala djurpark som är 14, 10, 8, 6 och 2 år gamla.
Följ dessa enkla steg för att hitta varians:
- Beräkna medelvärdet (enkelt medelvärde) för de fem siffrorna:
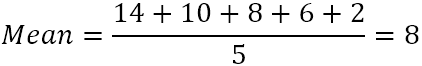
- Dra av medelvärdet från varje tal för att hitta skillnaderna. För att visualisera detta kan vi plotta skillnaderna i diagrammet:
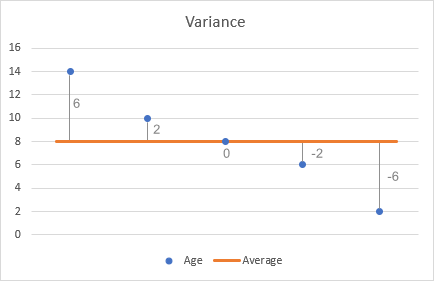
- Tvärsätt varje skillnad.
- Räkna ut medelvärdet av skillnaderna i kvadrat.
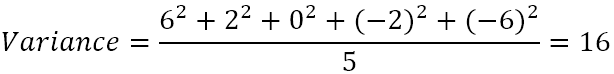
Variansen är alltså 16. Men vad betyder denna siffra egentligen?
I själva verket ger variansen bara en mycket allmän uppfattning om spridningen i datamängden. Ett värde på 0 innebär att det inte finns någon variabilitet, dvs. att alla siffror i datamängden är desamma. Ju större siffran är, desto mer utspridda är uppgifterna.
Det här exemplet gäller populationsvarians (dvs. 5 tigrar är hela den grupp som du är intresserad av). Om dina data är ett urval från en större population måste du beräkna stickprovsvariansen med hjälp av en något annorlunda formel.
Hur man beräknar varians i Excel
Det finns sex inbyggda funktioner för att beräkna varians i Excel: VAR, VAR.S, VARP, VAR.P, VARA och VARPA.
Ditt val av variansformel bestäms av följande faktorer:
- Den version av Excel som du använder.
- Om du beräknar variansen i urvalet eller i populationen.
- Om du vill utvärdera eller ignorera text och logiska värden.
Excel variansfunktioner
Tabellen nedan ger en översikt över de variationsfunktioner som finns i Excel för att hjälpa dig att välja den formel som passar bäst för dina behov.
| Namn | Excel-version | Datatyp | Text och logik |
| VAR | 2000 - 2019 | Exempel | Ignorerad |
| VAR.S | 2010 - 2019 | Exempel | Ignorerad |
| VARA | 2000 - 2019 | Exempel | Utvärderad |
| VARP | 2000 - 2019 | Befolkning | Ignorerad |
| VAR.P | 2010 - 2019 | Befolkning | Ignorerad |
| VARPA | 2000 - 2019 | Befolkning | Utvärderad |
VAR.S vs. VARA och VAR.P vs. VARPA
VARA och VARPA skiljer sig från andra variansfunktioner endast genom hur de hanterar logiska värden och textvärden i referenser. Följande tabell ger en sammanfattning av hur textrepresentationer av tal och logiska värden utvärderas.
| Typ av argument | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Logiska värden i matriser och referenser | Ignorerad | Utvärderad (SANT=1, FALSKT=0) |
| Textrepresentationer av tal i matriser och referenser | Ignorerad | Utvärderas som noll |
| Logiska värden och textrepresentationer av tal som skrivs in direkt i argumenten. | Utvärderad (SANT=1, FALSKT=0) Se även: Hur man tar bort dubbletter i Excel | |
| Tomma celler | Ignorerad | |
Hur man beräknar provvarians i Excel
A exempel är en uppsättning data som tagits ut ur hela populationen. Den varians som beräknas utifrån ett urval kallas för varians i stickprovet. .
Om du till exempel vill veta hur människors längd varierar skulle det vara tekniskt omöjligt att mäta alla människor på jorden. Lösningen är att ta ett urval av befolkningen, till exempel 1 000 personer, och uppskatta längden för hela befolkningen utifrån detta urval.
Provets varians beräknas med denna formel:
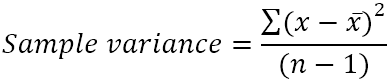
Var:
- x̄ är medelvärdet (enkelt medelvärde) av provvärdena.
- n är urvalets storlek, dvs. antalet värden i urvalet.
Det finns tre funktioner för att hitta variansen i Excel: VAR, VAR.S och VARA.
VAR-funktionen i Excel
Det är den äldsta Excel-funktionen för att uppskatta varians baserat på ett urval. VAR-funktionen finns i alla versioner av Excel 2000 till 2019.
VAR(number1, [number2], ...)Obs. I Excel 2010 ersattes funktionen VAR med VAR.S som ger bättre precision. Även om VAR fortfarande är tillgänglig för bakåtkompatibilitet rekommenderas det att använda VAR.S i de aktuella versionerna av Excel.
Funktionen VAR.S i Excel
Det är den moderna motsvarigheten till Excel-funktionen VAR.S. Använd funktionen VAR.S för att hitta variansen i Excel 2010 och senare.
VAR.S(nummer1, [nummer2], ...)VARA-funktionen i Excel
Excel-funktionen VARA returnerar en provvarians baserad på en uppsättning siffror, text och logiska värden som visas i tabellen.
VARA(värde1, [värde2], ...)Exempel på variansformel i Excel
När du arbetar med numeriska data kan du använda någon av ovanstående funktioner för att beräkna stickprovsvarians i Excel.
Låt oss till exempel ta reda på variansen för ett urval som består av 6 objekt (B2:B7) och använda en av nedanstående formler:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Som framgår av skärmbilden ger alla formlerna samma resultat (avrundat till två decimaler):
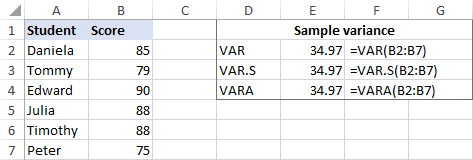
För att kontrollera resultatet kan vi göra var-beräkningen manuellt:
- Hitta medelvärdet med hjälp av funktionen AVERAGE:
=GENOMSNITT(B2:B7)Genomsnittet går till en tom cell, till exempel B8.
- Subtrahera genomsnittet från varje nummer i urvalet:
=B2-$B$8Skillnaderna hamnar i kolumn C, med början i C2.
- Kvadrera varje skillnad och för in resultatet i kolumn D, med början i D2:
=C2^2 - Addera de kvadrerade skillnaderna och dela resultatet med antalet föremål i urvalet minus 1:
=SUMMA(D2:D7)/(6-1)
Som du kan se är resultatet av vår manuella var-beräkning exakt detsamma som det antal som Excel:s inbyggda funktioner returnerar:
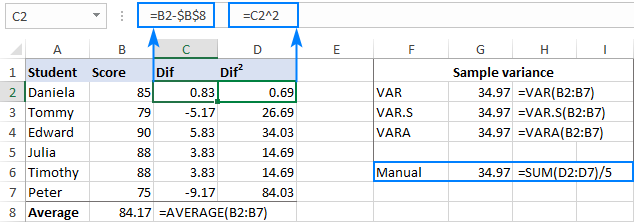
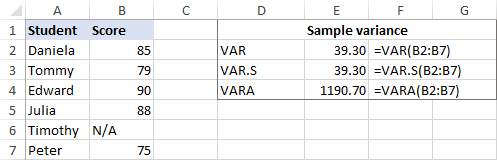
Om din datamängd innehåller Boolean och/eller text Värden ger VARA-funktionen ett annat resultat. Anledningen är att VAR och VAR.S ignorerar alla andra värden än siffror i referenser, medan VARA utvärderar textvärden som nollor, TRUE som 1 och FALSE som 0. Välj därför noggrant variansfunktionen för dina beräkningar beroende på om du vill bearbeta eller ignorera text och logiska värden.
Hur man beräknar befolkningsvarians i Excel
Befolkning är alla medlemmar i en viss grupp, dvs. alla observationer inom undersökningsområdet. Varians i befolkningen beskriver hur datapunkterna i hela populationen sprids ut.
Populationens varians kan beräknas med denna formel:
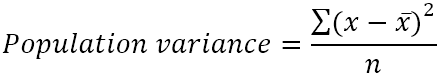
Var:
- x̄ är populationens medelvärde.
- n är populationens storlek, dvs. det totala antalet värden i populationen.
Det finns tre funktioner för att beräkna populationsvarians i Excel: VARP, VAR.P och VARPA.
VARP-funktionen i Excel
Excel-funktionen VARP returnerar variansen för en population baserat på hela mängden siffror. Funktionen finns i alla versioner av Excel 2000 till 2019.
VARP(number1, [number2], ...)Obs. I Excel 2010 ersattes VARP med VAR.P men finns fortfarande kvar för bakåtkompatibilitet. Det rekommenderas att använda VAR.P i de nuvarande versionerna av Excel eftersom det inte finns någon garanti för att VARP-funktionen kommer att finnas tillgänglig i framtida versioner av Excel.
Funktionen VAR.P i Excel
Det är en förbättrad version av VARP-funktionen som finns i Excel 2010 och senare.
VAR.P(nummer1, [nummer2], ...)VARPA-funktionen i Excel
Funktionen VARPA beräknar variansen för en population baserat på hela uppsättningen av siffror, text och logiska värden. Den finns tillgänglig i alla versioner av Excel 2000 till och med 2019.
VARA(värde1, [värde2], ...)Formel för befolkningsvarians i Excel
I exemplet för beräkning av var fann vi en varians för 5 provresultat, förutsatt att dessa resultat var ett urval från en större grupp elever. Om du samlar in data om alla elever i gruppen kommer dessa data att representera hela populationen, och du kommer att beräkna en populationsvarians med hjälp av ovanstående funktioner.
Låt oss säga att vi har provresultat för en grupp på 10 elever (B2:B11). Resultaten utgör hela populationen, så vi kommer att göra variationer med dessa formler:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
Alla formler kommer att ge samma resultat:
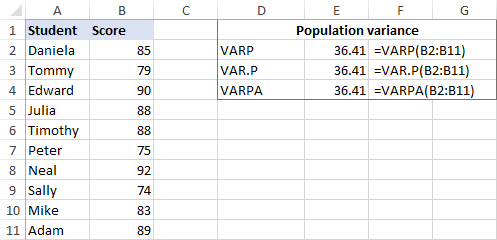
Om du vill vara säker på att Excel har gjort variansen rätt kan du kontrollera den med den manuella formeln för var-beräkning som visas i skärmdumpen nedan:

Om några av eleverna inte gjorde provet och har N/A i stället för ett poängnummer, kommer VARPA-funktionen att ge ett annat resultat. Anledningen är att VARPA utvärderar textvärden som nollor medan VARP och VAR.P ignorerar text- och logiska värden i referenser. Se VAR.P vs. VARPA för fullständig information.

Variansformel i Excel - användningsanvisningar
För att göra variansanalyser i Excel på rätt sätt ska du följa dessa enkla regler:
- Ange argument som värden, matriser eller cellreferenser.
- I Excel 2007 och senare kan du ange upp till 255 argument som motsvarar ett urval eller en population; i Excel 2003 och äldre - upp till 30 argument.
- För att utvärdera endast nummer i referenser, utan att ta hänsyn till tomma celler, text och logiska värden, använd funktionen VAR eller VAR.S för att beräkna variansen i urvalet och VARP eller VAR.P för att beräkna variansen i populationen.
- Att utvärdera logisk och text värden i referenser använder du VARA- eller VARPA-funktionen.
- Tillhandahålla minst två numeriska värden enligt en formel för provvarians och minst ett numeriskt värde till en formel för populationsvarians i Excel, annars uppstår felet #DIV/0!
- Argument som innehåller text som inte kan tolkas som siffror orsakar felet #VALUE!
Varians vs. standardavvikelse i Excel
Varians är utan tvekan ett användbart begrepp inom vetenskapen, men det ger väldigt lite praktisk information. Vi har till exempel tagit reda på åldrarna hos tigrarna i ett lokalt zoo och beräknat variansen, som är 16. Frågan är hur vi egentligen kan använda detta tal.
Du kan använda variansen för att räkna ut standardavvikelsen, som är ett mycket bättre mått på variationen i en datamängd.
Standardavvikelse beräknas som kvadratroten av variansen. Vi tar alltså kvadratroten av 16 och får standardavvikelsen 4.
I kombination med medelvärdet kan standardavvikelsen berätta hur gamla de flesta tigrarna är. Om till exempel medelvärdet är 8 och standardavvikelsen 4 är majoriteten av tigrarna i djurparken mellan 4 år (8 - 4) och 12 år (8 + 4).
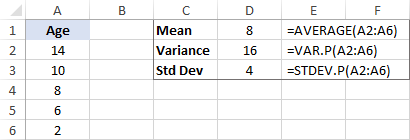
Microsoft Excel har särskilda funktioner för att beräkna standardavvikelsen för ett urval och en population. En detaljerad förklaring av alla funktioner finns i denna handledning: Hur man beräknar standardavvikelsen i Excel.
Så gör man varians i Excel. Om du vill titta närmare på de formler som diskuteras i den här handledningen är du välkommen att ladda ner vår exempelarbetsbok i slutet av det här inlägget. Jag tackar dig för att du läste och hoppas att vi ses på vår blogg nästa vecka!
Arbetsbok för praktiska övningar
Beräkna varians i Excel - exempel (.xlsx-fil)

