Мазмұны
Бұл оқулықта біз Excel-де дисперсия талдауын қалай жасау керектігін және таңдама мен жиынтық дисперсиясын табу үшін қандай формулаларды пайдалану керектігін қарастырамыз.
Дисперсиялық - ең пайдалылардың бірі. ықтималдықтар теориясы мен статистикадағы құралдар. Ғылымда деректер жиынындағы әрбір санның орташа мәннен қаншалықты алыс екенін сипаттайды. Іс жүзінде ол бір нәрсенің қаншалықты өзгеретінін жиі көрсетеді. Мысалы, экватор маңындағы температура басқа климаттық белдеулерге қарағанда аз ауытқуға ие. Бұл мақалада біз Excel-де дисперсияны есептеудің әртүрлі әдістерін талдаймыз.
Дисперсия дегеніміз не?
Дисперсиялық - өзгергіштік өлшемі. әртүрлі мәндердің қаншалықты таралатынын көрсететін деректер жиыны. Математикалық тұрғыдан ол орташа мәннен квадраттық айырмашылықтардың орташа мәні ретінде анықталады.
Дисперсиямен нақты нені есептеп жатқаныңызды жақсырақ түсіну үшін мына қарапайым мысалды қарастырыңыз.
Егер 5 бар делік. жергілікті хайуанаттар бағындағы 14, 10, 8, 6 және 2 жастағы жолбарыстар.
Айырмашылықты табу үшін мына қарапайым қадамдарды орындаңыз:
- Орташа мәнді есептеңіз (қарапайым орташа) бес санның:
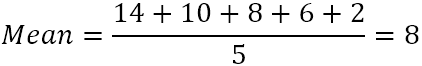
- Әр саннан орташа мәнді алып, айырмашылықтарын табыңыз. Мұны визуализациялау үшін диаграммадағы айырмашылықтарды салайық:
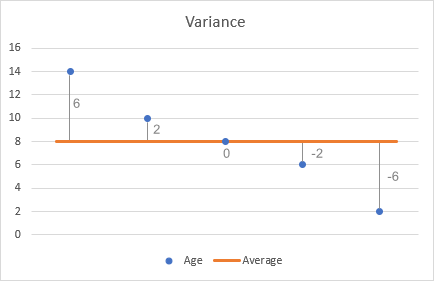
- Әр айырмашылықтың квадраты.
- Квадрат айырмаларының орташа мәнін есептеңіз.
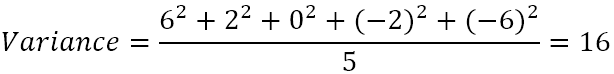
Демек, дисперсия 16. Бірақ бұл сан нені білдіреді?шын мәнінде білдіреді?
Шынында, дисперсия деректер жиынының дисперсиясы туралы өте жалпы түсінік береді. 0 мәні өзгермеліліктің жоқтығын білдіреді, яғни деректер жиынындағы барлық сандар бірдей. Сан неғұрлым үлкен болса, деректер соғұрлым көп таралады.
Бұл мысал популяция дисперсиясына арналған (яғни, 5 жолбарыс сізді қызықтыратын бүкіл топ). Егер деректеріңіз үлкенірек жиынтықтан таңдалған болса, онда сізге сәл басқа формуланы пайдаланып үлгі дисперсиясын есептеу керек.
Excel бағдарламасында дисперсияны қалай есептеу керек
6 ендірілген функция бар Excel бағдарламасында дисперсия жасау үшін: VAR, VAR.S, VARP, VAR.P, VARA және VARPA.
Сіздің дисперсия формуласын таңдау келесі факторлармен анықталады:
- Сіз пайдаланатын Excel нұсқасы.
- Үлгі немесе жиынтық дисперсиясын есептейсіз бе.
- Мәтін мен логикалық мәндерді бағалау немесе елемеу керек пе.
Excel дисперсия функциялары
Төмендегі кесте қажеттіліктеріңізге ең қолайлы формуланы таңдауға көмектесу үшін Excel бағдарламасында қолжетімді вариация функцияларына шолуды береді.
| Аты | Excel нұсқасы | Дерек түрі | Мәтін және логика |
| VAR | 2000 - 2019 | Үлгі | Еленбеген |
| VAR.S | 2010 - 2019 | Үлгі | Еленбеген |
| ВАРА | 2000 -2019 | Үлгі | Бағаланған |
| VARP | 2000 - 2019 | Халық | Еленбейді |
| VAR.P | 2010 - 2019 | Халық | Елденбейді |
| VARPA | 2000 - 2019 | Тұрғындар | Бағаланған |
VAR.S қарсы VARA және VAR.P қарсы VARPA
VARA және VARPA басқа дисперсия функцияларынан тек сілтемелердегі логикалық және мәтіндік мәндерді өңдеу тәсілімен ғана ерекшеленеді. Төмендегі кестеде сандар мен логикалық мәндердің мәтіндік көріністері қалай бағаланатынының қысқаша мазмұны берілген.
| Аргумент түрі | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Массивтер мен сілтемелердегі логикалық мәндер | Еленбеген | Бағаланған (TRUE=1, FALSE=0) |
| Массивтер мен сілтемелер ішіндегі сандардың мәтіндік көріністері | Еленбейді | Нөл ретінде бағаланады |
| Логикалық мәндері және тікелей аргументтерге терілген сандардың мәтіндік көрінісі | Бағаланған (ШЫНДЫҚ=1, ЖАЛҒАН=0) | |
| Бос ұяшықтар | Еленбеген | |
Excel бағдарламасында таңдау дисперсиясын қалай есептеу керек
A үлгі - бүкіл жиынтықтан алынған деректер жинағы. Ал таңдама бойынша есептелетін дисперсия үлгі дисперсиясы деп аталады.
Мысалы, адамдардың бойының қалай өзгеретінін білгіңіз келсе, әр адамды өлшеу техникалық тұрғыдан мүмкін емес. жер.Шешім – популяцияның іріктемесін, айталық, 1000 адам және сол іріктеу негізінде бүкіл популяцияның биіктігін бағалау.
Үлгідегі дисперсия мына формуламен есептеледі:
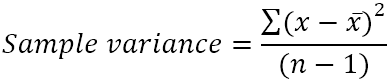
Мұндағы:
- x̄ - таңдама мәндерінің орташа (қарапайым орташа мәні).
- n - іріктеу өлшемі, яғни. үлгі.
Excel бағдарламасында үлгі дисперсиясын табудың 3 функциясы бар: VAR, VAR.S және VARA.
Excel бағдарламасындағы VAR функциясы
Бұл ең көне функция. Үлгіге негізделген дисперсияны бағалау үшін Excel функциясы. VAR функциясы Excel 2000 және 2019 нұсқасының барлық нұсқаларында қол жетімді.
VAR(1-сан, [2-сан], …)Ескертпе. Excel 2010 нұсқасында VAR функциясы жақсартылған дәлдікті қамтамасыз ететін VAR.S функциясымен ауыстырылды. VAR кері үйлесімділік үшін әлі қол жетімді болса да, Excel бағдарламасының ағымдағы нұсқаларында VAR.S пайдалану ұсынылады.
Excel бағдарламасындағы VAR.S функциясы
Бұл Excel бағдарламасының заманауи аналогы. VAR функциясы. Excel 2010 және одан кейінгі нұсқаларында үлгі дисперсиясын табу үшін VAR.S функциясын пайдаланыңыз.
VAR.S(1-сан, [2-сан], …)Excel бағдарламасындағы VARA функциясы
Excel VARA функциясы қайтарады осы кестеде көрсетілгендей сандар, мәтін және логикалық мәндер жиынына негізделген үлгі дисперсиясы.
VARA(1-мән, [2-мән], …)Excel бағдарламасындағы үлгі дисперсия формуласы
Жұмыс кезінде үлгі дисперсиясын есептеу үшін жоғарыдағы функциялардың кез келгенін пайдалануға болатын деректердің сандық жиыныExcel-де.
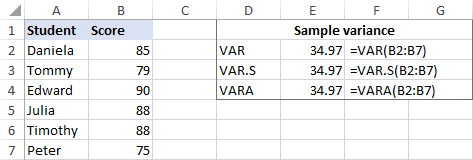
Мысал ретінде 6 элементтен тұратын үлгінің дисперсиясын табайық (B2:B7). Ол үшін төмендегі формулалардың бірін пайдалануға болады:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Скриншотта көрсетілгендей, барлық формулалар бірдей нәтиже (2 ондық таңбаға дейін дөңгелектенеді):
Нәтижені тексеру үшін var есебін қолмен жасайық:
- Орташа мәнді қолданып табыңыз AVERAGE функциясы:
=AVERAGE(B2:B7)Орташа мән кез келген бос ұяшыққа өтеді, айталық B8.
- Үлгідегі әрбір саннан орташа мәнді алып тастаңыз:
=B2-$B$8Айырмашылықтар C2 бағанынан басталады.
- Әр айырмашылықтың квадратын шығарыңыз және нәтижелерді D2 бағанына қойыңыз:
=C2^2Сондай-ақ_қараңыз: Шарттары бар ең үлкен мәнді табу үшін Excel MAX IF формуласы - Квадрат айырмасын қосыңыз және нәтижені санға бөліңіз. үлгідегі элементтер минус 1:
=SUM(D2:D7)/(6-1)
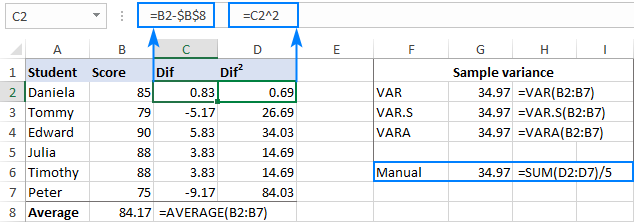
Көріп отырғаныңыздай, қолмен бар есептеу нәтижесі Excel бағдарламасының кірістірілген функциялары қайтарған санмен дәл бірдей:
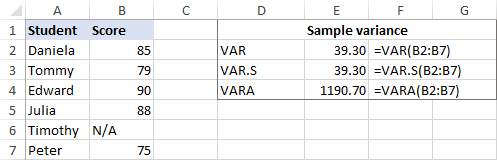
Егер деректер жинағында Логикалық және/немесе мәтін мәндері болса, VARA функциясы басқа нәтиже береді. Себебі VAR және VAR.S сілтемелердегі сандардан басқа кез келген мәндерді елемейді, ал VARA мәтін мәндерін нөл ретінде, TRUE мәнін 1 және ЖАЛҒАН мәнін 0 ретінде бағалайды. Сондықтан есептеулеріңіз үшін дисперсия функциясын мұқият таңдаңыз. мәтінді және логиканы өңдеуді немесе елемеуді қалайды.
ҚалайExcel бағдарламасында популяция дисперсиясын есептеңіз
Популяция берілген топтың барлық мүшелері, яғни зерттеу саласындағы барлық бақылаулар. Популяцияның дисперсиясы бүкіл деректер нүктелерінің қалай болатынын сипаттайды популяция таралған.
Популяция дисперсиясын мына формула арқылы табуға болады:
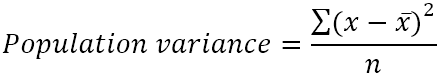
Мұндағы:
- x̄ - популяцияның орташа мәні.
- n - жалпы саны, яғни жиынтықтағы мәндердің жалпы саны.
Excel бағдарламасында жиынтық дисперсиясын есептеу үшін 3 функция бар: VARP, VAR .P және VARPA.
Excel бағдарламасындағы VARP функциясы
Excel VARP функциясы барлық сандар жиынына негізделген жиынтықтың дисперсиясын қайтарады. Ол Excel 2000 және 2019 нұсқасының барлық нұсқаларында қол жетімді.
VARP(1-нөмір, [2-нөмір], …)Ескертпе. Excel 2010 нұсқасында VARP VAR.P нұсқасымен ауыстырылды, бірақ кері үйлесімділік үшін әлі де сақталады. Excel бағдарламасының ағымдағы нұсқаларында VAR.P пайдалану ұсынылады, себебі VARP функциясы Excel бағдарламасының болашақ нұсқаларында қолжетімді болатынына кепілдік жоқ.
Excel бағдарламасындағы VAR.P функциясы
Бұл Excel 2010 және одан кейінгі нұсқаларында қол жетімді VARP функциясының жетілдірілген нұсқасы.
VAR.P(1-сан, [2-сан], …)Excel бағдарламасындағы VARPA функциясы
VARPA функциясы дисперсияны есептейді. сандардың, мәтіннің және логикалық мәндердің барлық жиынына негізделген жиынтық. Ол Excel 2000 және 2019 нұсқасының барлық нұсқаларында қолжетімді.
VARA(1-мән,[2 мән], …)Excel бағдарламасындағы популяция дисперсиясының формуласы
Үлгідегі бар есептеу мысалында біз 5 емтихан ұпайының дисперсиясын таптық, бұл ұпайлар үлкенірек студенттер тобының таңдауы болды. Топтағы барлық студенттер туралы деректерді жинасаңыз, бұл деректер бүкіл жиынтықты көрсетеді және жоғарыда аталған функцияларды пайдалану арқылы жиынтық дисперсиясын есептейсіз.
Айталық, бізде топтың емтихан ұпайлары бар. 10 оқушыдан (B2:B11). Ұпайлар бүкіл жиынтықты құрайды, сондықтан біз мына формулалармен дисперсия жасаймыз:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
Және барлық формулалар бірдей нәтиже:
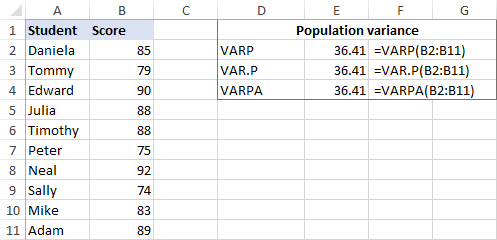
Excel дисперсияны дұрыс жасағанына көз жеткізу үшін оны төмендегі скриншотта көрсетілген қолмен бар есептеу формуласымен тексеруге болады:

Егер кейбір студенттер емтиханға қатыспаса және ұпай санының орнына N/A болса, VARPA функциясы басқа нәтиже береді. Себебі VARPA мәтін мәндерін нөл ретінде бағалайды, ал VARP және VAR.P сілтемелердегі мәтін мен логикалық мәндерді елемейді. Толық мәліметтерді VAR.P және VARPA қараңыз.

Excel бағдарламасындағы дисперсия формуласы - пайдалану ескертпесі
Excel бағдарламасында дисперсияны талдауды дұрыс жасау үшін келесі әрекеттерді орындаңыз мына қарапайым ережелер:
- Аргументтерді мәндер, массивтер немесе ұяшық сілтемелері ретінде беріңіз.
- Excel 2007 және одан кейінгі нұсқаларында келесіге сәйкес келетін 255-ке дейін аргумент беруге болады.үлгі немесе популяция; Excel 2003 және одан жоғары нұсқаларында - 30 аргументке дейін.
- Бос ұяшықтарды, мәтінді және логикалық мәндерді елемей, сілтемелердегі сандарды ғана бағалау үшін VAR немесе VAR.S функциясын пайдаланыңыз. таңдау дисперсиясын есептеңіз және жиынтық дисперсияны табу үшін VARP немесе VAR.P.
- Сілтемелердегі логикалық және мәтін мәндерін бағалау үшін VARA немесе VARPA функциясын пайдаланыңыз.
- Үлгі дисперсия формуласына кемінде екі сандық мәнді және Excel бағдарламасындағы жиынтық дисперсия формуласына кемінде бір сандық мәнді беріңіз, әйтпесе #DIV/0! қате орын алды.
- Сан ретінде түсіндірілмейтін мәтіні бар аргументтер #VALUE! қателер.
Excel бағдарламасындағы стандартты ауытқуға қарсы дисперсия
Дисперсиялық ғылымда сөзсіз пайдалы ұғым, бірақ ол өте аз практикалық ақпарат береді. Мысалы, біз жергілікті хайуанаттар бағында жолбарыстардың популяциясының жасын анықтадық және дисперсияны есептедік, ол 16-ға тең. Бұл санды қалай пайдалана аламыз? стандартты ауытқу, бұл деректер жиынындағы вариация көлемінің әлдеқайда жақсы көрсеткіші.
Стандартты ауытқу дисперсияның квадрат түбірі ретінде есептеледі. Сонымен, біз 16-ның квадрат түбірін алып, 4-тің стандартты ауытқуын аламыз.
Орташа мәнмен бірге стандартты ауытқу жолбарыстардың көпшілігінің қанша жаста екенін айта алады. Мысалы, егерорташа 8 және стандартты ауытқу 4, хайуанаттар бағындағы жолбарыстардың көпшілігі 4 жас (8 - 4) пен 12 жас (8 + 4) арасында.
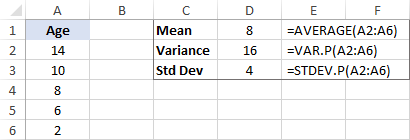
Microsoft Excel бағдарламасында үлгі мен жиынтықтың стандартты ауытқуын өңдеуге арналған арнайы функциялар бар. Барлық функциялардың егжей-тегжейлі түсіндірмесін осы оқулықтан табуға болады: Excel бағдарламасында стандартты ауытқуды қалай есептеу керек.
Excel бағдарламасында дисперсияны осылай жасауға болады. Осы оқулықта талқыланған формулаларды толығырақ көру үшін осы жазбаның соңындағы жұмыс кітабының үлгісін жүктеп алуыңызға болады. Оқығаныңыз үшін алғыс айтамын және келесі аптада блогымызда көреміз деп үміттенемін!
Тәжірибелік жұмыс кітабы
Excel бағдарламасында ауытқуды есептеу - мысалдар (.xlsx файлы)

