Sisällysluettelo
Tässä opetusohjelmassa tarkastelemme, miten Excelissä tehdään varianssianalyysi ja mitä kaavoja käytetään otoksen ja populaation varianssin määrittämiseen.
Varianssi on yksi todennäköisyysteorian ja tilastotieteen hyödyllisimmistä työkaluista. Tieteessä se kuvaa, kuinka kaukana kukin luku aineistossa on keskiarvosta. Käytännössä se usein osoittaa, kuinka paljon jokin asia muuttuu. Esimerkiksi lämpötilalla päiväntasaajan läheisyydessä on vähemmän varianssia kuin muilla ilmastovyöhykkeillä. Tässä artikkelissa analysoimme erilaisia menetelmiä varianssin laskemiseen Excelissä.
Mitä on varianssi?
Poikkeama on tietokokonaisuuden vaihtelun mitta, joka osoittaa, kuinka paljon eri arvot ovat hajallaan. Matemaattisesti se määritellään keskiarvosta poikkeavien neliöerojen keskiarvona.
Jotta ymmärtäisit paremmin, mitä varianssilla oikeastaan lasketaan, katso tätä yksinkertaista esimerkkiä.
Oletetaan, että paikallisessa eläintarhassasi on viisi tiikeriä, jotka ovat 14, 10, 8, 6 ja 2-vuotiaita.
Löydät varianssin noudattamalla seuraavia yksinkertaisia ohjeita:
- Laske viiden luvun keskiarvo (yksinkertainen keskiarvo):
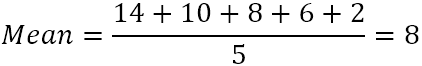
- Vähennä jokaisesta luvusta keskiarvo, jotta saat erot selville. Havainnollistetaan tämä piirtämällä erot kaavioon:
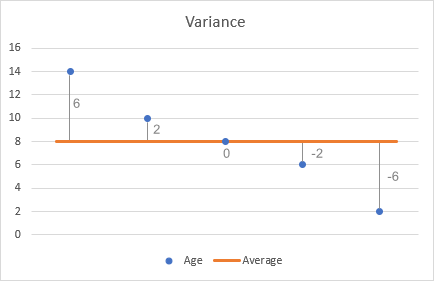
- Neliöi jokainen ero.
- Laske neliöerojen keskiarvo.
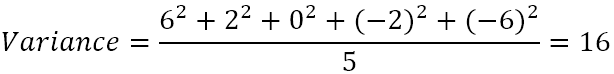
Poikkeama on siis 16. Mutta mitä tämä luku oikeastaan tarkoittaa?
Todellisuudessa varianssi antaa vain hyvin yleisen käsityksen aineiston hajonnasta. Arvo 0 tarkoittaa, että vaihtelua ei ole, eli kaikki aineiston luvut ovat samanlaisia. Mitä suurempi luku on, sitä enemmän aineisto on hajallaan.
Tämä esimerkki koskee populaatiovarianssia (eli 5 tiikeriä on koko ryhmä, josta olet kiinnostunut). Jos aineistosi on valinta suuremmasta populaatiosta, sinun on laskettava otosvarianssi hieman eri kaavalla.
Miten lasketaan varianssi Excelissä
Excelissä on kuusi sisäänrakennettua funktiota varianssin määrittämiseen: VAR, VAR.S, VARP, VAR.P, VARA ja VARPA.
Varianssikaavan valinta riippuu seuraavista tekijöistä:
- Käyttämäsi Excel-versio.
- Lasketaanko otoksen vai populaation varianssi.
- Haluatko arvioida vai jättää huomiotta teksti- ja loogiset arvot.
Excelin varianssitoiminnot
Alla olevassa taulukossa on yleiskatsaus Excelissä käytettävissä olevista muunnosfunktioista, jotta voit valita tarpeisiisi parhaiten sopivan kaavan.
| Nimi | Excel-versio | Tietotyyppi | Teksti ja logiikat |
| VAR | 2000 - 2019 | Näyte | Ei huomioitu |
| VAR.S | 2010 - 2019 | Näyte | Ei huomioitu |
| VARA | 2000 - 2019 | Näyte | Arvioitu |
| VARP | 2000 - 2019 | Väestö | Ei huomioitu |
| VAR.P | 2010 - 2019 | Väestö | Ei huomioitu |
| VARPA | 2000 - 2019 | Väestö | Arvioitu |
VAR.S vs. VARA ja VAR.P vs. VARPA
VARA ja VARPA eroavat muista varianssitoiminnoista vain siinä, miten ne käsittelevät loogisia ja tekstiarvoja viitteissä. Seuraavassa taulukossa on yhteenveto siitä, miten numeroiden ja loogisten arvojen tekstiedustukset arvioidaan.
| Argumentin tyyppi | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Loogiset arvot matriisien ja viittausten sisällä | Ei huomioitu | Arvioitu (TRUE=1, FALSE=0) |
| Numeroiden tekstimuotoiset esitykset matriiseissa ja viittauksissa | Ei huomioitu | Arvioidaan nollaksi |
| Loogiset arvot ja numeroiden tekstimuotoiset esitykset, jotka on kirjoitettu suoraan argumentteihin. | Arvioitu (TRUE=1, FALSE=0) | |
| Tyhjät solut | Ei huomioitu | |
Otoksen varianssin laskeminen Excelissä
A näyte on koko perusjoukosta poimittu aineistojoukko. Ja otoksesta laskettua varianssia sanotaan näytteen varianssi .
Jos esimerkiksi halutaan tietää, miten ihmisten pituudet vaihtelevat, olisi teknisesti mahdotonta mitata kaikkia maapallon ihmisiä. Ratkaisu on ottaa otos väestöstä, esimerkiksi 1000 ihmistä, ja arvioida koko väestön pituudet otoksen perusteella.
Otoksen varianssi lasketaan tällä kaavalla:
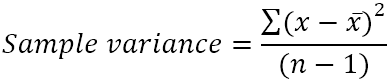
Missä:
- x̄ on otosarvojen keskiarvo (yksinkertainen keskiarvo).
- n on otoskoko eli otoksen sisältämien arvojen lukumäärä.
Excelissä on kolme funktiota otosvarianssin löytämiseksi: VAR, VAR.S ja VARA.
VAR-toiminto Excelissä
Se on vanhin Excel-funktio, jolla estimoidaan varianssia otokseen perustuen. VAR-funktio on käytettävissä kaikissa Excelin versioissa 2000-2019.
VAR(numero1, [numero2], ...)Huomautus: Excel 2010:ssä VAR-funktio korvattiin VAR.S-toiminnolla, joka tarjoaa paremman tarkkuuden. Vaikka VAR on edelleen käytettävissä taaksepäin yhteensopivuuden vuoksi, on suositeltavaa käyttää VAR.S-toimintoa nykyisissä Excel-versioissa.
VAR.S-toiminto Excelissä
Se on nykyaikainen vastine Excelin VAR-funktiolle. Käytä VAR.S-funktiota otantavarianssin määrittämiseen Excel 2010:ssä ja uudemmissa ohjelmissa.
VAR.S(numero1, [numero2], ...)VARA-toiminto Excelissä
Excelin VARA-funktio palauttaa näytteen varianssista, joka perustuu numeroiden, tekstin ja loogisten arvojen joukkoon, kuten tässä taulukossa on esitetty.
VARA(arvo1, [arvo2], ...)Esimerkki varianssikaavasta Excelissä
Kun työskentelet numeeristen tietojen kanssa, voit käyttää mitä tahansa edellä mainittuja funktioita otantavarianssin laskemiseen Excelissä.
Esimerkkinä on, että etsitään 6 kappaleesta (B2:B7) koostuvan otoksen varianssi. Tähän voit käyttää jotakin alla olevista kaavoista:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Kuten kuvakaappauksessa näkyy, kaikki kaavat antavat saman tuloksen (pyöristettynä kahteen desimaaliin):
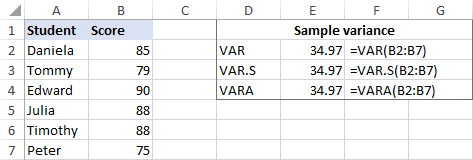
Tarkistetaan tulos tekemällä var-laskenta manuaalisesti:
- Etsi keskiarvo käyttämällä AVERAGE-funktiota:
=KESKIARVO(B2:B7)Keskiarvo siirtyy mihin tahansa tyhjään soluun, esimerkiksi B8:aan.
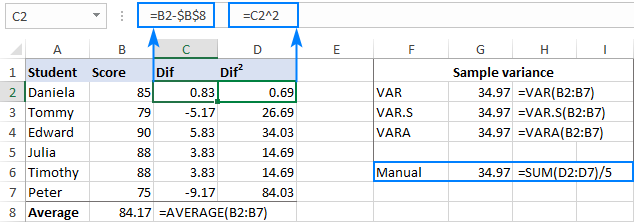
- Vähennä keskiarvo jokaisesta otoksen luvusta:
=B2-$B$8Erot siirretään sarakkeeseen C, alkaen sarakkeesta C2.
- Neliöi jokainen erotus ja siirrä tulokset sarakkeeseen D, alkaen D2:sta:
=C2^2 - Laske yhteen neliöerot ja jaa tulos otoksen kohteiden lukumäärällä miinus 1:
=SUMMA(D2:D7)/(6-1)
Kuten näet, manuaalisen var-laskennan tulos on täsmälleen sama kuin Excelin sisäänrakennettujen funktioiden palauttama luku:
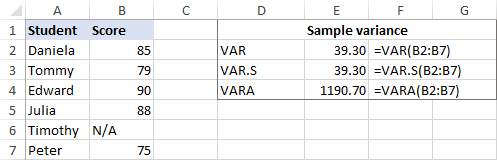
Jos aineistosi sisältää Boolean ja/tai teksti arvot, VARA-funktio palauttaa eri tuloksen. Syynä on se, että VAR ja VAR.S eivät huomioi muita arvoja kuin numeroita viittauksissa, kun taas VARA arvioi tekstiarvot nollina, TRUE arvona 1 ja FALSE arvona 0. Valitse siis varianssifunktio laskelmissasi huolellisesti sen mukaan, haluatko käsitellä vai jättää huomiotta tekstiä ja loogisia arvoja.
Kuinka laskea populaation varianssi Excelissä
Väestö on kaikki tietyn ryhmän jäsenet, eli kaikki havainnot tutkimusalueella. Väestön varianssi kuvaa, miten koko populaation datapisteet jakautuvat.
Populaation varianssi voidaan määrittää tällä kaavalla:
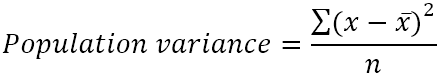
Missä:
- x̄ on populaation keskiarvo.
- n on populaation koko eli populaatiossa olevien arvojen kokonaismäärä.
Excelissä on kolme funktiota populaatiovarianssin laskemiseen: VARP, VAR.P ja VARPA.
VARP-toiminto Excelissä
Excelin VARP-funktio palauttaa perusjoukon varianssin koko lukujoukon perusteella. Se on käytettävissä kaikissa Excelin versioissa 2000-2019.
VARP(numero1, [numero2], ...)Huomautus: Excel 2010:ssä VARP korvattiin VAR.P:llä, mutta se säilytetään edelleen taaksepäin yhteensopivuuden vuoksi. On suositeltavaa käyttää VAR.P:tä nykyisissä Excel-versioissa, koska ei ole mitään takeita siitä, että VARP-toiminto on käytettävissä tulevissa Excel-versioissa.
VAR.P-toiminto Excelissä
Se on parannettu versio Excel 2010:ssä ja sitä uudemmissa versioissa käytettävissä olevasta VARP-toiminnosta.
VAR.P(numero1, [numero2], ...)VARPA-toiminto Excelissä
VARPA-funktio laskee perusjoukon varianssin, joka perustuu numeroiden, tekstin ja loogisten arvojen kokonaisuuteen. Se on käytettävissä kaikissa Excel 2000-2019 -versioissa.
VARA(arvo1, [arvo2], ...)Väestön varianssin kaava Excelissä
Esimerkin varianssilaskentaesimerkissä löysimme viiden koepistemäärän varianssin olettaen, että kyseiset pisteet olivat valinta suuremmasta opiskelijaryhmästä. Jos keräät tietoja kaikista ryhmän opiskelijoista, nämä tiedot edustavat koko perusjoukkoa, ja voit laskea perusjoukon varianssin käyttämällä edellä mainittuja funktioita.
Oletetaan, että meillä on 10 opiskelijan ryhmän (B2:B11) tenttipisteet. Pisteet muodostavat koko perusjoukon, joten teemme varianssin näillä kaavoilla:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
Ja kaikki kaavat palauttavat identtisen tuloksen:
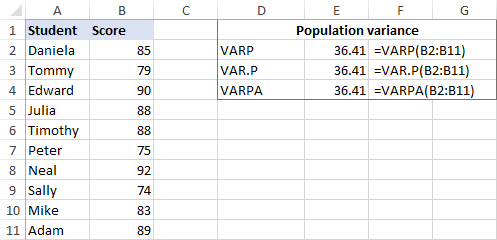
Jos haluat varmistaa, että Excel on tehnyt varianssin oikein, voit tarkistaa sen alla olevassa kuvakaappauksessa näkyvän manuaalisen varianssin laskentakaavan avulla:

Jos osa opiskelijoista ei osallistunut kokeeseen ja heillä on pistenumeron sijasta N/A, VARPA-funktio palauttaa erilaisen tuloksen. Syynä on se, että VARPA arvioi tekstiarvot nollina, kun taas VARP ja VAR.P eivät huomioi teksti- ja loogisia arvoja viitteissä. Katso lisätietoja kohdasta VAR.P vs. VARPA.

Varianssin kaava Excelissä - käyttöohjeet
Jos haluat tehdä varianssianalyysin Excelissä oikein, noudata näitä yksinkertaisia sääntöjä:
- Anna argumentit arvoina, malleina tai soluviittauksina.
- Excel 2007:ssä ja sitä uudemmissa versioissa voit antaa enintään 255 argumenttia, jotka vastaavat otosta tai populaatiota; Excel 2003:ssa ja sitä vanhemmissa versioissa - enintään 30 argumenttia.
- Arvioida vain numerot käyttämällä VAR- tai VAR.S-funktiota otosvarianssin laskemiseen ja VARP- tai VAR.P-funktiota populaatiovarianssin määrittämiseen, kun viitteissä ei oteta huomioon tyhjiä soluja, tekstiä ja loogisia arvoja.
- Arvioida looginen ja teksti arvot viitteissä, käytä VARA- tai VARPA-funktiota.
- Tarjota vähintään kaksi numeerista arvoa otoksen varianssikaavaan ja vähintään yksi numeerinen arvo Excelissä olevaan populaatiovarianssin kaavaan, muuten tulee virhe #DIV/0!.
- Argumentit, jotka sisältävät tekstiä, jota ei voida tulkita numeroiksi, aiheuttavat #VALUE! -virheitä.
Varianssi vs. keskihajonta Excelissä
Varianssi on epäilemättä hyödyllinen käsite luonnontieteissä, mutta se antaa hyvin vähän käytännön tietoa. Löysimme esimerkiksi paikallisen eläintarhan tiikeripopulaation iät ja laskimme varianssin, joka on 16. Kysymys kuuluu: miten voimme käyttää tätä lukua?
Voit käyttää varianssia keskihajonnan laskemiseen, joka on paljon parempi mittari vaihtelun määrän mittaamiseen tietosarjassa.
Keskihajonta lasketaan varianssin neliöjuurena. Otetaan siis neliöjuuri 16:sta ja saadaan keskihajonnaksi 4.
Yhdessä keskiarvon kanssa keskihajonta voi kertoa, kuinka vanhoja suurin osa tiikereistä on. Jos keskiarvo on esimerkiksi 8 ja keskihajonta 4, suurin osa eläintarhan tiikereistä on iältään 4-vuotiaita (8 - 4) ja 12-vuotiaita (8 + 4).
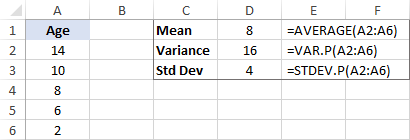
Microsoft Excelissä on erityisiä funktioita otoksen ja perusjoukon keskihajonnan laskemiseen. Kaikkien funktioiden yksityiskohtainen selitys on tässä opetusohjelmassa: Keskihajonnan laskeminen Excelissä.
Näin varianssi tehdään Excelissä. Jos haluat tutustua tarkemmin tässä ohjeessa käsiteltyihin kaavoihin, voit ladata esimerkkityökirjan tämän viestin lopussa. Kiitos lukemisesta ja toivottavasti tapaamme blogissamme ensi viikolla!
Harjoitustyökirja
Varianssin laskeminen Excelissä - esimerkkejä (.xlsx-tiedosto)

