Зміст
У цьому уроці ми розглянемо, як робити дисперсійний аналіз Excel і які формули використовувати для знаходження дисперсії вибірки і генеральної сукупності.
Дисперсія - один з найкорисніших інструментів в теорії ймовірностей і статистиці. У науці вона описує, наскільки далеко кожне число в наборі даних знаходиться від середнього значення. На практиці вона часто показує, наскільки сильно щось змінюється. Наприклад, температура біля екватора має меншу дисперсію, ніж в інших кліматичних зонах. У цій статті ми розберемо різні методи розрахунку дисперсії в Excel.
Що таке дисперсія?
Відхилення це міра мінливості набору даних, яка показує, наскільки далеко розкидані різні значення. Математично вона визначається як середнє квадратичне відхилення від середнього значення.
Для того, щоб краще зрозуміти, що ви насправді розраховуєте за допомогою відхилення, розглянемо цей простий приклад.
Припустимо, що у вашому місцевому зоопарку є 5 тигрів віком 14, 10, 8, 6 і 2 роки.
Щоб знайти відхилення, виконайте ці прості кроки:
- Обчислити середнє арифметичне (середнє арифметичне) з п'яти чисел:
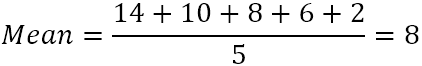
- Від кожного числа відніміть середнє, щоб знайти різницю. Для наочності побудуємо графік різниць на діаграмі:
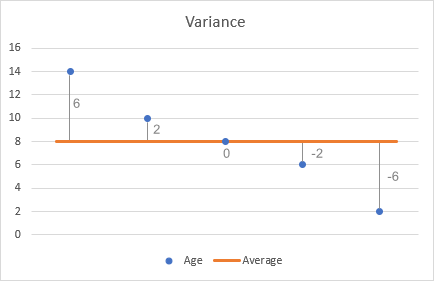
- Піднесіть кожну різницю до квадрата.
- Обчислити середнє арифметичне з квадратів різниць.
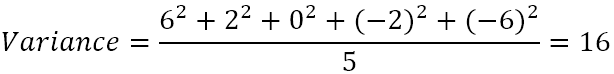
Отже, розбіжність становить 16. Але що насправді означає ця цифра?
Насправді, дисперсія дає лише дуже загальне уявлення про дисперсію набору даних. Значення 0 означає, що варіація відсутня, тобто всі числа в наборі даних однакові. Чим більше число, тим більше розкидані дані.
Цей приклад стосується дисперсії популяції (тобто 5 тигрів - це вся група, яка вас цікавить). Якщо ваші дані є вибіркою з більшої популяції, то вам потрібно розрахувати дисперсію вибірки за дещо іншою формулою.
Як розрахувати дисперсію в Excel
В Excel є 6 вбудованих функцій для розрахунку дисперсій: VAR, VAR.S, VARP, VAR.P, VARA та VARPA.
Вибір формули дисперсії визначається наступними факторами:
- Версію Excel, яку ви використовуєте.
- Незалежно від того, чи розраховуєте ви вибіркову або генеральну дисперсію.
- Чи хочете ви оцінювати або ігнорувати текстові та логічні значення.
Дисперсійні функції Excel
У наведеній нижче таблиці наведено огляд варіаційних функцій, доступних в Excel, щоб допомогти вам вибрати формулу, яка найкраще відповідає вашим потребам.
| Ім'я та прізвище | Версія в Excel | Тип даних | Текст і логіка |
| VAR | 2000 - 2019 | Зразок | Ігнорується |
| VAR.S | 2010 - 2019 | Зразок | Ігнорується |
| VARA | 2000 - 2019 | Зразок | Оцінено |
| VARP | 2000 - 2019 | Населення | Ігнорується |
| VAR.P | 2010 - 2019 | Населення | Ігнорується |
| VARPA | 2000 - 2019 | Населення | Оцінено |
VAR.S проти VARA та VAR.P проти VARPA
VARA і VARPA відрізняються від інших дисперсійних функцій лише способом обробки логічних і текстових значень у посиланнях. У наступній таблиці наведено стислий опис того, як оцінюються текстові представлення чисел і логічних значень.
| Тип аргументу | VAR, VAR.S, VARP, VARP, VAR.P | VARA & VARPA |
| Логічні значення в масивах і посиланнях | Ігнорується | Оцінено (TRUE=1, FALSE=0) |
| Текстове представлення чисел у масивах та посиланнях | Ігнорується | Оцінюється як нуль |
| Логічні значення та текстові представлення чисел, що вводяться безпосередньо в аргументи | Оцінено (TRUE=1, FALSE=0) | |
| Порожні клітинки | Ігнорується | |
Як розрахувати дисперсію вибірки в Excel
A зразок це сукупність даних, витягнутих з усієї генеральної сукупності. А дисперсія, розрахована за вибіркою, називається дисперсія вибірки .
Наприклад, якщо ви хочете знати, як змінюється зріст людей, то технічно неможливо виміряти кожну людину на землі. Рішення полягає в тому, щоб взяти вибірку населення, скажімо, 1000 осіб, і оцінити зріст всього населення на основі цієї вибірки.
Вибіркова дисперсія розраховується за такою формулою:
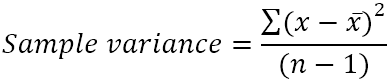
Де:
- x̄ - середнє (середнє арифметичне) вибіркових значень.
- n - обсяг вибірки, тобто кількість значень у вибірці.
Для знаходження вибіркової дисперсії в Excel існує 3 функції: VAR, VAR.S та VARA.
VAR-функція в Excel
Це найстаріша функція Excel для оцінки дисперсії на основі вибірки. Функція VAR доступна у всіх версіях Excel від 2000 до 2019 року.
Примітка: в Excel 2010 функція VAR була замінена на VAR.S, яка забезпечує кращу точність. Хоча VAR все ще доступна для зворотної сумісності, рекомендується використовувати VAR.S в поточних версіях Excel.
Функція VAR.S в Excel
Це сучасний аналог функції Excel VAR. Використовуйте функцію VAR.S для знаходження дисперсії вибірки в Excel 2010 і новіших версіях.
VAR.S(number1, [number2], ...)Функція VARA в Excel
Функція Excel VARA повертає вибіркову дисперсію на основі набору чисел, тексту та логічних значень, як показано в цій таблиці.
VARA(значення1, [значення2], ...)Приклад формули дисперсії в Excel
При роботі з числовим набором даних можна скористатися будь-якою з наведених вище функцій для розрахунку вибіркової дисперсії в Excel.
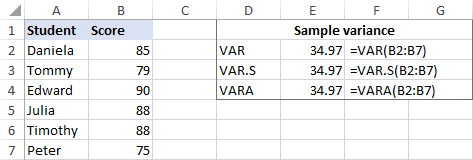
Для прикладу знайдемо дисперсію вибірки, що складається з 6 елементів (B2:B7). Для цього можна скористатися однією з наведених нижче формул:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Як показано на скріншоті, всі формули повертають однаковий результат (округлений до 2 знаків після коми):
Для перевірки результату зробимо розрахунок var вручну:
- Знайдіть середнє значення за допомогою функції СРЗНАЧ за допомогою функції СРЗНАЧ:
=СЕРЕДНЄ(B2:B7)Середнє значення переноситься в будь-яку порожню клітинку, скажімо, В8.
- Відніміть середнє значення від кожного числа у вибірці:
=B2-$B$8Різниці переносяться до колонки С, починаючи з С2.
- Піднесіть кожну різницю до квадрату і занесіть результати в колонку D, починаючи з D2:
=C2^2 - Складіть квадрати різниць і поділіть результат на кількість елементів у вибірці мінус 1:
=SUM(D2:D7)/(6-1)
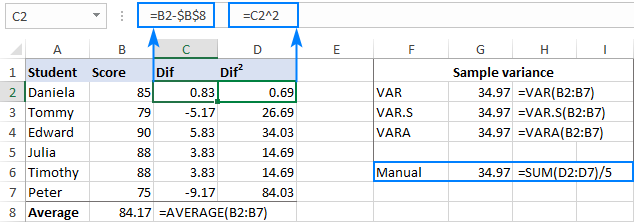
Як бачимо, результат нашого ручного обчислення var точно збігається з числом, яке повертають вбудовані функції Excel:
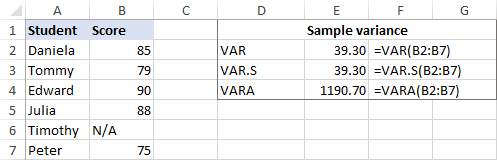
Якщо ваш набір даних містить Boolean та/або текст Причина в тому, що VAR і VAR.S ігнорують будь-які інші значення, крім чисел у посиланнях, тоді як VARA оцінює текстові значення як нулі, TRUE - як 1, а FALSE - як 0. Тому, будь ласка, уважно обирайте дисперсійну функцію для своїх розрахунків залежно від того, чи хочете ви обробляти або ігнорувати текст і логічні значення.
Як розрахувати дисперсію населення в Excel
Населення це всі члени даної групи, тобто всі спостереження в досліджуваній сфері. Різниця в чисельності населення описує, як розподілені точки даних у всій сукупності.
Дисперсію чисельності населення можна знайти за такою формулою:
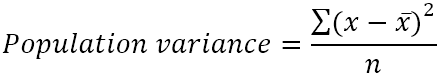
Де:
- x̄ - середня чисельність населення.
- n - обсяг генеральної сукупності, тобто загальна кількість значень у генеральній сукупності.
Для розрахунку дисперсії населення в Excel існує 3 функції: VARP, VAR.P та VARPA.
Функція VARP в Excel
Функція Excel VARP повертає дисперсію сукупності на основі всього набору чисел. Вона доступна у всіх версіях Excel від 2000 до 2019 року.
VARP(номер1, [номер2], ...)Примітка: В Excel 2010 функція VARP була замінена на VAR.P, але все ще зберігається для забезпечення зворотної сумісності. Рекомендується використовувати VAR.P в поточних версіях Excel, оскільки немає гарантії, що функція VARP буде доступна в майбутніх версіях Excel.
Функція VAR.P в Excel
Це вдосконалена версія функції VARP, доступна в Excel 2010 і новіших версіях.
VAR.P(номер1, [номер2], ...)Функція VARPA в Excel
Функція VARPA обчислює дисперсію сукупності на основі всього набору чисел, тексту та логічних значень. Вона доступна у всіх версіях Excel з 2000 по 2019 рік.
VARA(значення1, [значення2], ...)Формула дисперсії населення в Excel
У прикладі розрахунку вибіркової дисперсії ми знайшли дисперсію 5 іспитових балів, припускаючи, що ці бали були вибіркою з більшої групи студентів. Якщо ви зберете дані про всіх студентів у групі, ці дані представлятимуть всю сукупність, і ви розрахуєте дисперсію сукупності, використовуючи наведені вище функції.
Скажімо, у нас є екзаменаційні бали групи з 10 студентів (В2:В11). Ці бали складають генеральну сукупність, тому ми будемо робити дисперсію за цими формулами:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
І всі формули повертатимуть ідентичний результат:
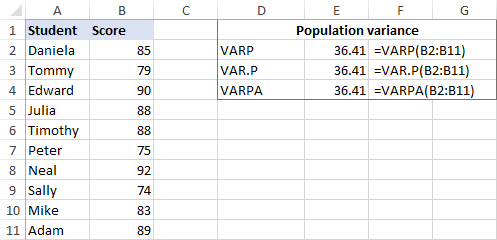
Щоб переконатися, що Excel правильно розрахував дисперсію, ви можете перевірити її за допомогою формули розрахунку дисперсії вручну, показаної на скріншоті нижче:

Якщо деякі студенти не складали іспит і замість номера балу мають значення N/A, функція VARPA поверне інший результат. Причина полягає в тому, що VARPA оцінює текстові значення як нулі, тоді як VARP і VAR.P ігнорують текстові та логічні значення в посиланнях. Будь ласка, дивіться VAR.P vs. VARPA для отримання більш детальної інформації.

Формула дисперсії в Excel - примітки щодо використання
Щоб правильно виконати дисперсійний аналіз в Excel, будь ласка, дотримуйтесь цих простих правил:
- Надавати аргументи у вигляді значень, масивів або посилань на комірки.
- В Excel 2007 і новіших версіях можна ввести до 255 аргументів, що відповідають вибірці або генеральній сукупності; в Excel 2003 і старіших версіях - до 30 аргументів.
- Оцінювати тільки цифри у посиланнях, ігноруючи порожні клітинки, текст та логічні значення, використовуйте функцію VAR або VAR.S для обчислення вибіркової дисперсії та VARP або VAR.P для знаходження генеральної дисперсії.
- Оцінити логічний і текст значення в посиланнях, використовуйте функцію VARA або VARPA.
- Забезпечити щонайменше два числових значення до формули вибіркової дисперсії та щонайменше одне числове значення до формули дисперсії сукупності в Excel, інакше виникне помилка #DIV/0!
- Аргументи, що містять текст, який не може бути інтерпретований як числа, викликають помилки #VALUE!
Дисперсія проти середньоквадратичного відхилення в Excel
Дисперсія, безперечно, є корисним поняттям у науці, але вона дає дуже мало практичної інформації. Наприклад, ми знайшли вік популяції тигрів у місцевому зоопарку і вирахували дисперсію, яка дорівнює 16. Виникає питання - як ми можемо насправді використовувати це число?
Ви можете використовувати дисперсію для обчислення середньоквадратичного відхилення, яке є набагато кращим показником кількості варіації в наборі даних.
Середньоквадратичне відхилення розраховується як квадратний корінь з дисперсії. Отже, ми беремо квадратний корінь з 16 і отримуємо стандартне відхилення 4.
У поєднанні з середнім значенням стандартне відхилення може сказати вам, скільки років більшості тигрів. Наприклад, якщо середнє значення дорівнює 8, а стандартне відхилення - 4, більшість тигрів у зоопарку мають вік від 4 років (8 - 4) до 12 років (8 + 4).
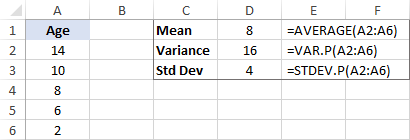
Microsoft Excel має спеціальні функції для обчислення середньоквадратичного відхилення вибірки та генеральної сукупності. Детальне пояснення всіх функцій можна знайти в цьому уроці: Як обчислити середньоквадратичне відхилення в Excel.
Ось як зробити дисперсію в Excel. Щоб ближче познайомитися з формулами, розглянутими в цьому підручнику, ви можете завантажити наш зразок робочого зошита в кінці цієї статті. Дякую за прочитання і сподіваюся побачити вас на нашому блозі на наступному тижні!
Практичний посібник
Розрахунок дисперсії в Excel - приклади (файл .xlsx)

